Bewegungsdiagramme bei gleichmäßiger Impulszunahme (gleichmäßig beschleunigte Bewegung): Unterschied zwischen den Versionen

Aus Schulphysikwiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „===Versuch: Ein Wagen rollt berab=== [[Bild:Versuchsaufbau_Wagen_rollt_bergab_Ultraschall.jpg‎|thumb|300px|Der Versuchsaufbau mit dem Ultraschallentfernungsmess…“)
 
K (→‎Ergebnis)
 
(6 dazwischenliegende Versionen des gleichen Benutzers werden nicht angezeigt)
Zeile 4: Zeile 4:
 
Ein kleiner Wagen wird auf eine schräggestellte Schiene gesetzt und losgelassen. Am Ende der Schiene bremst etwas Knete den Wagen.
 
Ein kleiner Wagen wird auf eine schräggestellte Schiene gesetzt und losgelassen. Am Ende der Schiene bremst etwas Knete den Wagen.
  
−
Mit Hilfe eines Ultraschallsensors kann dabei der Ort des Wagens bestimmt werden, wobei das Ortskoordinatensystem gerade die Schiene selbst ist. Am Anfang der Schiene ist er Nullpunkt. Den Sensor muss man so platzieren, dass er den Nullpunkt auch korrekt misst.  
+
Mit Hilfe eines Ultraschallsensors kann dabei der Ort des Wagens bestimmt werden, wobei das Ortskoordinatensystem gerade die Schiene selbst ist. Den Nullpunkt kann man beliebig setzen, z.B. an den linken Rand der Schiene.
  
 
====Messung====
 
====Messung====
−
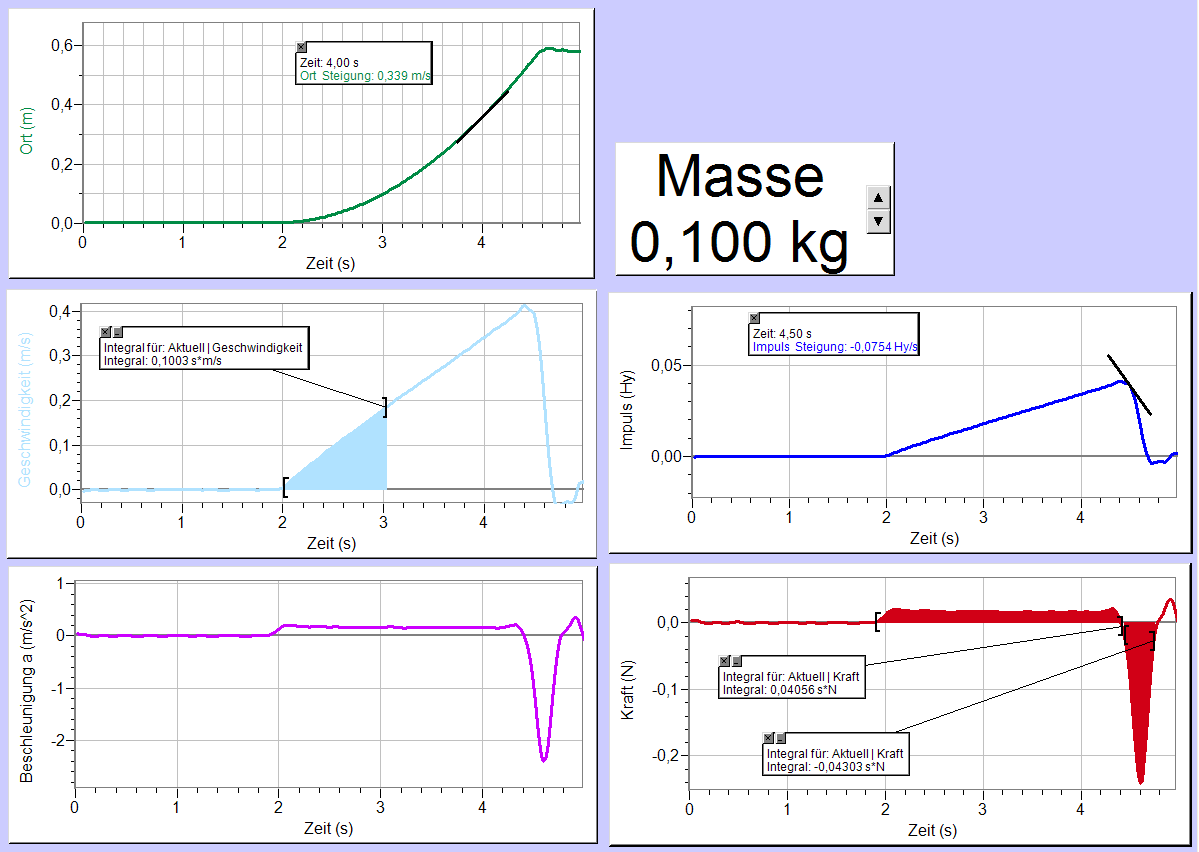
[[Bild:Wagen_rollt_bergab_Diagramme.png|707px|thumb||none|Das Orts- Geschwindigkeits- und Beschleunigungsdiagramm]]
+
[[Datei:Bewegungsdiagramme gleichmäßig beschleuinigte Bewegung (Vernier).png|1199px|thumb|none|Diagramme über die Zeit von Ort, Geschwindigkeit, Beschleunigung, Impuls und Kraft.]]
−
 
+
 
====Ergebnis====
 
====Ergebnis====
 +
;Im Wasserbehältermodell
 +
Die gefundene gleichmäßige Zunahme von Impuls und Geschwindigkeit ist nicht überraschend. Eine konstante Kraft entspricht im Wasserbehältermodell einer gleichmäßigen Zunahme der Wassermenge (Impuls) und damit auch der Wasserhöhe (Geschwindigkeit).
 +
 +
Das Modell kann allerdings keine Aussagen über den Ort des Wagens machen!
 +
 +
;Zahlenwerte
 +
Das Impulsdiagramm liefert folgendes:
 +
:Der Impuls hat gleichmäßig zugenommen. Innerhalb von 2,5s um 0,04 Hy.
 +
 +
:Die Impulszunahme, also die Kraft, war in etwa konstant. Sie entspricht der Steigung im Diagramm und beträgt
 +
 +
:<math>F=\frac{\triangle p}{\triangle t}=\frac{0{,}04\rm Hy}{2{,5}\rm s} = 0{,}016\rm N</math>
 +
 +
:Die Hangabtriebskraft war also um 0,016 Newton größer als die Reibungskraft. Das ist nicht viel und entspricht der Gewichtskraft von 1,6 Gramm.
 +
 +
:Das Abbremsen ging viel schneller als das Beschleunigen. Innerhalb von nur 0,2s sinkt die Impulsmenge um 0,04Hy. Außerdem war die Kraft, also die Impulsänderung, beim Bremsen nicht konstant. Die mittlere Kraft entspricht der mittleren Steigung und betrug
 +
 +
:<math>\bar F=\frac{-0{,}04\rm Hy}{0{,}2\rm s} = -0,2\rm N</math>
 +
:Man hätte den Wagen also mit einer Kraft von 0,2 Newton, die 0,2 Sekunden lang wirkt abbremsen können.
 +
 +
 +
Das Kraftdiagramm bestätigt die am Geschwindigkeitsdiagramm gefundenen Aussagen.
 +
:Die Fläche unter dem Diagramm entspricht der Impulsänderung.
 +
:Während der Beschleunigung kommen ca. 0,04 Hy dazu, beim Abbremsen sinkt die Impulsmenge wieder auf Null.
 +
 +
 
Am Ortsdiagramm kann man folgendes ablesen:  
 
Am Ortsdiagramm kann man folgendes ablesen:  
−
:Der Wagen befindet sich zunächst ca. 25cm rechts vom Anfang der Schiene. Nach ca. 1,5sec wurde er losgelassen und erreicht das Ende der Schiene nach ca. 3,7sec. Während seiner Fahrt wurde er immer schneller.
+
:Der Wagen befindet sich zunächst am Anfang der Schiene. Nach ca. zwei Sekunden wurde er losgelassen und erreicht den Knetklumpen nach ca. 4,5 Sekunden. Während seiner Fahrt wurde er immer schneller. Der Knetklumpen lag 0,6m vom linken Rand entfernt.
 +
 
  
 
Das Geschwindigkeitsdiagramm liefert folgendes:
 
Das Geschwindigkeitsdiagramm liefert folgendes:
−
:Die Geschwindigkeit hat gleichmäßig zugenommen. Innerhalb von 2,3sec um 0,6 m/sec.
+
:Die Geschwindigkeit hat gleichmäßig zugenommen. Innerhalb von 2,5s um 0,4 m/s.
 +
 
 +
:Die Beschleunigung beim Bergabrollen war also in etwa konstant. Sie beträgt
  
−
:Die Beschleunigung beim Bergabrollen war also in etwa konstant, das heisst die mittlere und die momentane Beschleunigung stimmen überein. Die Steigung von Sekante und Tangente sind identisch. Sie beträgt
+
:<math>a=\frac{0{,}4\rm\frac{m}{sec}}{2{,5}\rm s} = 0{,}16\rm \frac{m}{s^2}</math>
  
−
:<math>a=\frac{0,6\frac{m}{sec}}{2,3 sec} = 0,26 \frac{m}{sec^2}</math>
+
:Das Abbremsen ging viel schneller als das Beschleunigen. Innerhalb von nur 0,2s fiel die Geschwindigkeit um 0,4m/sec. Außerdem war die Beschleunigung beim Bremsen nicht konstant. Die mittlere Beschleunigung betrug
  
−
:Das Abbremsen ging viel schneller als das Beschleunigen. Innerhalb von nur 0,2sec fiel die Geschwindigkeit um 0,6m/sec. Ausserdem war die Beschleunigung beim Bremsen nicht konstant. Die mittlere Beschleunigung betrug
+
:<math>\bar a=\frac{-0{,}4\rm\frac{m}{s}}{0{,}2\rm s} = -2\rm \frac{m}{s^2}</math>
  
−
:<math>\bar a=\frac{-0,6\frac{m}{sec}}{0,2 sec} = -3 \frac{m}{sec^2}</math>
 
  
 
Das Beschleunigungsdiagamm bestätigt die am Geschwindigkeitsdiagramm gefundenen Aussagen.
 
Das Beschleunigungsdiagamm bestätigt die am Geschwindigkeitsdiagramm gefundenen Aussagen.

Aktuelle Version vom 20. November 2015, 22:00 Uhr

Versuch: Ein Wagen rollt berab

Der Versuchsaufbau mit dem Ultraschallentfernungsmesser

Aufbau

Ein kleiner Wagen wird auf eine schräggestellte Schiene gesetzt und losgelassen. Am Ende der Schiene bremst etwas Knete den Wagen.

Mit Hilfe eines Ultraschallsensors kann dabei der Ort des Wagens bestimmt werden, wobei das Ortskoordinatensystem gerade die Schiene selbst ist. Den Nullpunkt kann man beliebig setzen, z.B. an den linken Rand der Schiene.

Messung

Diagramme über die Zeit von Ort, Geschwindigkeit, Beschleunigung, Impuls und Kraft.

Ergebnis

Im Wasserbehältermodell

Die gefundene gleichmäßige Zunahme von Impuls und Geschwindigkeit ist nicht überraschend. Eine konstante Kraft entspricht im Wasserbehältermodell einer gleichmäßigen Zunahme der Wassermenge (Impuls) und damit auch der Wasserhöhe (Geschwindigkeit).

Das Modell kann allerdings keine Aussagen über den Ort des Wagens machen!

Zahlenwerte

Das Impulsdiagramm liefert folgendes:

Der Impuls hat gleichmäßig zugenommen. Innerhalb von 2,5s um 0,04 Hy.
Die Impulszunahme, also die Kraft, war in etwa konstant. Sie entspricht der Steigung im Diagramm und beträgt
[math]F=\frac{\triangle p}{\triangle t}=\frac{0{,}04\rm Hy}{2{,5}\rm s} = 0{,}016\rm N[/math]
Die Hangabtriebskraft war also um 0,016 Newton größer als die Reibungskraft. Das ist nicht viel und entspricht der Gewichtskraft von 1,6 Gramm.
Das Abbremsen ging viel schneller als das Beschleunigen. Innerhalb von nur 0,2s sinkt die Impulsmenge um 0,04Hy. Außerdem war die Kraft, also die Impulsänderung, beim Bremsen nicht konstant. Die mittlere Kraft entspricht der mittleren Steigung und betrug
[math]\bar F=\frac{-0{,}04\rm Hy}{0{,}2\rm s} = -0,2\rm N[/math]
Man hätte den Wagen also mit einer Kraft von 0,2 Newton, die 0,2 Sekunden lang wirkt abbremsen können.


Das Kraftdiagramm bestätigt die am Geschwindigkeitsdiagramm gefundenen Aussagen.

Die Fläche unter dem Diagramm entspricht der Impulsänderung.
Während der Beschleunigung kommen ca. 0,04 Hy dazu, beim Abbremsen sinkt die Impulsmenge wieder auf Null.


Am Ortsdiagramm kann man folgendes ablesen:

Der Wagen befindet sich zunächst am Anfang der Schiene. Nach ca. zwei Sekunden wurde er losgelassen und erreicht den Knetklumpen nach ca. 4,5 Sekunden. Während seiner Fahrt wurde er immer schneller. Der Knetklumpen lag 0,6m vom linken Rand entfernt.


Das Geschwindigkeitsdiagramm liefert folgendes:

Die Geschwindigkeit hat gleichmäßig zugenommen. Innerhalb von 2,5s um 0,4 m/s.
Die Beschleunigung beim Bergabrollen war also in etwa konstant. Sie beträgt
[math]a=\frac{0{,}4\rm\frac{m}{sec}}{2{,5}\rm s} = 0{,}16\rm \frac{m}{s^2}[/math]
Das Abbremsen ging viel schneller als das Beschleunigen. Innerhalb von nur 0,2s fiel die Geschwindigkeit um 0,4m/sec. Außerdem war die Beschleunigung beim Bremsen nicht konstant. Die mittlere Beschleunigung betrug
[math]\bar a=\frac{-0{,}4\rm\frac{m}{s}}{0{,}2\rm s} = -2\rm \frac{m}{s^2}[/math]


Das Beschleunigungsdiagamm bestätigt die am Geschwindigkeitsdiagramm gefundenen Aussagen.

Von „http://schulphysikwiki.de/index.php?title=Bewegungsdiagramme_bei_gleichmäßiger_Impulszunahme_(gleichmäßig_beschleunigte_Bewegung)&oldid=10399“