Zeigermodell und Wellengleichung einer ebenen harmonischen Welle: Unterschied zwischen den Versionen

Version vom 28. Januar 2016, 12:46 Uhr (Quelltext anzeigen) Patrick.Nordmann (Diskussion | Beiträge) (→‎Wellengleichung) ← Zum vorherigen Versionsunterschied		Version vom 28. Januar 2016, 12:50 Uhr (Quelltext anzeigen) Patrick.Nordmann (Diskussion | Beiträge) (→‎Wellengleichung) Zum nächsten Versionsunterschied →
Zeile 58:		Zeile 58:
	:<math>y(x,t) = \hat y \, \sin(\omega t - \Delta\varphi(x))</math>		:<math>y(x,t) = \hat y \, \sin(\omega t - \Delta\varphi(x))</math>
−	Eine Schwingung, die eine halbe Wellenlänge vom "Start" entfernt ist, hinkt gerade um <math>\pi</math> hinterher. Erst eine Schwingung, die eine ganze Wellenlänge vom "Start" entfernt ist, hinkt um <math>2 \pi</math> hinterher und ist damit wieder in Phase. Bestimmt man den Abstand <math>x</math> von der Quelle in Wellenlängen, so gibt dieser gerade die Phasenverschiebung in Einheiten von <math>2\,\pi</math> an:	+	Eine Schwingung, die eine halbe Wellenlänge von der Quelle entfernt ist, hinkt gerade um <math>\pi</math> hinterher. Erst eine Schwingung, die eine ganze Wellenlänge von der Quelle entfernt ist, hinkt um <math>2 \pi</math> hinterher und ist damit wieder in Phase. Bestimmt man den Abstand <math>x</math> von der Quelle in Wellenlängen, so gibt dieser gerade die Phasenverschiebung in Einheiten von <math>2\,\pi</math> an:
	Bei diesem Beispiel beträgt die Wellenlänge <math>\lambda = 3\,\rm m</math>:		Bei diesem Beispiel beträgt die Wellenlänge <math>\lambda = 3\,\rm m</math>:
	:<math>		:<math>
−	\begin{array}{rclcll}	+	\begin{array}{lcll}
−	x &=& 6\,\rm m    &=& 2\,\lambda &\Rightarrow&  \Delta \varphi = 2\cdot 2\pi \approx 12{,}6\\	+	x = 6\,\rm m    &=& 2\,\lambda &\Rightarrow&  \Delta \varphi = 2\cdot 2\pi \approx 12{,}6\\
−	x &=& 4{,}5\,\rm m    &=& 1{,5}\,\lambda &\Rightarrow&  \Delta \varphi = 1{,5}\cdot 2\pi \approx 4{,}7\\	+	x = 4{,}5\,\rm m    &=& 1{,5}\,\lambda &\Rightarrow&  \Delta \varphi = 1{,5}\cdot 2\pi \approx 9{,}4\\
−	x &=& 3{,}3\,\rm m    &=& 1{,}1\,\lambda &\Rightarrow&  \Delta \varphi = 1{,}1\cdot 2\pi \approx 6{,}9\\	+	x = 3{,}3\,\rm m    &=& 1{,}1\,\lambda &\Rightarrow&  \Delta \varphi = 1{,}1\cdot 2\pi \approx 6{,}9\\
	\end{array}		\end{array}

---

Version vom 28. Januar 2016, 12:50 Uhr

(Kursstufe > Mechanische Wellen)

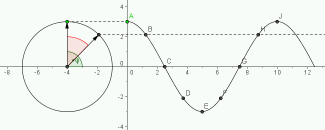
Im Falle einer räumlich unbegrenzten, linearen harmonischen Welle kann man die Welle relativ einfach beschreiben. In einer solchen Welle sind alle Schwingungen harmonisch und die Welle breitet sich nur längs einer Raumrichtung aus. Kugelwellen, Kreiswellen oder Zylinderwellen sind also keine solchen Wellen, ebene Wellen schon. Außerdem werden räumlich begrenzte Wellenpakete ausgeschlossen.

Bei einer Welle regt eine Schwingung ihren Nachbarn in Ausbreitungsrichtung zu erzwungenen Schwingungen an. Alle schwingen mit der gleichen Frequenz und der gleichen Amplitude. Die Schwinger hinken aber in Ausbreitungsrichtung der ursprünglichen Schwingung hinterher, wodurch sich eine Phasenverschiebung ergibt. Im Abstand einer halben Wellenlänge beträgt sie gerade

$$\pi$$ , so dass die Schwingungen gegenphasig sind, bei einer ganzen Wellenlänge sind es $$2 \ \pi$$ , womit die Schwingungen wieder in Phase sind.

Zeigermodell

Eine Schwingung wird durch einen rotierenden Zeiger dargestellt. Eine Welle wird durch eine Kette von Schwingungen, also auch durch eine Kette von Zeigern dargestellt. Die Zeiger haben eine Phasenverschiebung zum Nachbarzeiger, weil das "Signal" verzögert weitergegeben wird.

Sehr anschaulich gibt diese Idee eine Spirale wieder. Sobald sie sich dreht, sieht man eine Welle nach oben oder unten laufen, je nach Drehrichtung.

• (Video der sich drehenden Windspirale)

Bei der Holzspirale entsprechen den einzelnen Holzstäben die Zeiger, die durch ihre Drehung von der Seite betrachtet die Schwingung an einem Ort beschreiben. Jedes Holzstäbchen wird zum Nachbarstäbchen ein bischen gedreht. (Genau genommen sieht man zwei Wellen, weil die Stäbchen zu lang sind.)

• (Video der sich drehenden Holzspirale)

Zum Selberbasteln kann man sich diesen Schnittbogen ausschneiden und aufhängen.

Ähnlich anschaulich sind die auf einem Modell sich drehenden Perlen, die auch schrittweise um einen festen Winkel phasenverschoben sind.

Animationen

Diese Animation veranschaulicht die Zeigerdarstellung einer Welle. An jeder Stelle der Welle befindet sich ein drehender Zeiger. Leider drehen sich die Zeiger dabei nicht quer zur Ausbreitungsrichtung, sondern parallel dazu. Das entspricht einer Longitudinalwelle und nicht einer Transversalwelle. Anders ist die Darstellung zweidimensional nicht möglich, aber es kann auch verwirren.

Die Animation kann mit der Pausetaste links unten angehalten werden.

Der linke Zeiger gehört zum Anfangspunkt A der Welle. Der rechte Zeiger ist am blauen Punkt verschiebbar und gehört zur Stelle B. Angegeben ist der Phasenunterschied der Zeiger an den verschiedenen Orten.

Hier kann man sich die Geogebradatei herunterladen.

In dieser Animation von Jörg Bogendörfer sind viele Zeiger einer Welle dargestellt. Auch hier drehen sich die Zeiger nicht quer zur Ausbreitungsrichtung sondern parallel dazu.

Wellengleichung

Die Wellengleichung soll "sagen" wie groß die Auslenkung der Welle an einem bestimmten Ort und zu einem bestimmten Zeitpunkt ist. Dazu stellt man für alle beteiligten Schwinger eine Ortsfunktion auf. Da die Ortsfunktionen von der Position x abhängen, schreibt man

$$y_x(t)$$ oder $$y(x,t)$$ . Alle Ortsfunktionen zusammen nennt man Wellengleichung.

Jede der einzelnen harmonischen Schwingungen hat die gleiche Frequenz und die gleiche Amplitude. Sie unterscheiden sich nur durch eine ortsabhängige Phasenverschiebung voneinander^[1]:

$$y(x,t) = \hat y \, \sin(\omega t - \Delta\varphi(x))$$

Eine Schwingung, die eine halbe Wellenlänge von der Quelle entfernt ist, hinkt gerade um

$$\pi$$ hinterher. Erst eine Schwingung, die eine ganze Wellenlänge von der Quelle entfernt ist, hinkt um $$2 \pi$$ hinterher und ist damit wieder in Phase. Bestimmt man den Abstand $$x$$ von der Quelle in Wellenlängen, so gibt dieser gerade die Phasenverschiebung in Einheiten von $$2\,\pi$$ an:

Bei diesem Beispiel beträgt die Wellenlänge

$$\lambda = 3\,\rm m$$ :

$$\begin{array}{lcll} x = 6\,\rm m &=& 2\,\lambda &\Rightarrow& \Delta \varphi = 2\cdot 2\pi \approx 12{,}6\\ x = 4{,}5\,\rm m &=& 1{,5}\,\lambda &\Rightarrow& \Delta \varphi = 1{,5}\cdot 2\pi \approx 9{,}4\\ x = 3{,}3\,\rm m &=& 1{,}1\,\lambda &\Rightarrow& \Delta \varphi = 1{,}1\cdot 2\pi \approx 6{,}9\\ \end{array}$$

Die ortsabhängige Phasenverschiebung beträgt also

$$\Delta\varphi(x) = \frac{x}{\lambda}\,2\pi = \frac{2 \pi}{\lambda} x \qquad.$$ (Der Bruch $$\frac{2 \pi}{\lambda}$$ wird auch als Wellenzahl bezeichnet.) Und es folgt:

$$y(x,t) = \hat y \, \sin(\omega t - \frac{2 \pi}{\lambda} x)$$

Auch zwei weitere Umformungen dieser Gleichungen findet man häufig.

Die erste verwendet die Periodendauer statt der Frequenz und ist schön symmetrisch. Sie folgt aus

$$\omega = 2 \pi \, f = \frac{2\pi}{T}$$ .

Die zweite verwendet die Ausbreitungsgeschwindigkeit der Welle. Sie folgt aus

$$\frac{2\pi}{\lambda} = \frac{2\pi\, f}{\lambda\, f} = \frac{\omega}{c}$$ .

Im Abstand $$x$$ von der Quelle hinkt die Schwingung um die Phase $$\Delta \varphi$$ hinterher: $$\frac{\Delta\varphi}{2\pi}=\frac{x}{\lambda}\qquad \Delta\varphi = \frac{x}{\lambda}\,2\pi = \frac{2 \pi}{\lambda} x$$ Wellengleichung einer linearen harmonischen Welle: $$\begin{array}{rcl} y(x,t) &=& \hat y \, \sin\,(\omega t - \frac{2 \pi}{\lambda} x) \\ &=& \hat y \, \sin\left( 2\pi ( \frac{t}{T} - \frac{x}{\lambda}) \right) \\ &=&\hat y \, \sin\left( \frac{2\pi}{\lambda } \left( c \, t - x\right) \right) \end{array}$$

Beispiel

Es soll eine passende Gleichung für die drehende Windspirale aufgestellt werden.

Wir nehmen an, dass sie sich in der Sekunde zweimal dreht, der Radius beträgt drei Zentimeter und die Wellenlänge 13 Zentimeter. Dementsprechend gilt also:

$$f= \rm 2 \, Hz \ \ (\omega=2\pi \cdot 2 Hz)\quad {;} \quad \hat y = 3 \, cm \quad {;} \quad \lambda=13\, cm$$

$$y(x,t) = \rm 3\, cm \, \sin(4 \pi \, Hz \ t - \frac{2 \pi}{13\, cm} \ x) \approx 3\, cm \, \sin(12 \, Hz \ t - 0{,}48 \frac{1}{cm} \ x)$$

Im Argument des Sinus beschreibt

$$\rm 12 \, \frac{1}{s}$$ wie sich der Zeiger mit der Zeit dreht und $$\rm - 0{,}48 \frac{1}{cm}$$ wie sich die Phase des Zeigers mit dem Ort verändert.

In der zweiten Version sieht das mit einer Periode von

$$\rm T = 0{,}5 \, s$$ und einer Wellenlänge von $$\rm \lambda = 13 \, cm$$ so aus:

$$y(x,t) = \rm 3\, cm \, \sin\left[ 2 \pi \left( \frac{t}{0{,}5 \, s} - \frac{x}{13\, cm} \right) \right]$$

Und in der dritten Version mit der Phasengeschwindigkeit

$$c = \lambda \, f = \rm 13\,cm \cdot 0{,5}\,Hz = 2{,}6\,\frac{cm}{s}$$ so:

$$y(x,t) = \rm 3\, cm \, \sin\left[ \frac{2 \pi}{13\,cm} \left( 2{,}6\,\frac{cm}{s} \, t - x \right) \right] \approx \rm 3\, cm \, \sin\left[ 0{,}48 \frac{1}{cm} \left( 2{,}6\,\frac{cm}{s} \, t - x \right) \right]$$

Folgerungen

Nun kann man für einen beliebigen Ort das Ortsgesetz der Schwingung bestimmen. Am Anfang (x=0) und nach 13 oder 26,... Zentimetern der Spirale gilt:

$$y(t)=\rm 3\, cm \, \sin(12 \, Hz \ t )$$

Eine halbe Wellenlänge oder 6,5 cm weiter unten (und entsprechend 13 + 6,5 cm ...) hat man eine Phasenverschiebung von

$$\pi$$ :

$$y(t)=\rm 3\, cm \, \sin(12 \, Hz \ t - 0{,}48\, \frac{1}{cm} \ 6{,}5\, cm) = 3\, cm \, \sin(12 \, Hz \ t - 3{,}12)$$

Man kann außerdem für eine feste Zeit für alle beteiligten Schwingungen (hier eigentlich drehende Zeiger) die momentane Elongation (Auslenkung) angeben. Das entspricht dem momentanen Aussehen der Welle.

Zu Beginn (t=0) sieht die Welle so aus:

$$y(x)=\rm 3\, cm \, \sin(- 0{,}48\, \frac{1}{cm} \ x)$$

Nach einer viertel Sekunde ist sie genau eine halbe Wellenlänge weitergewandert:

$$y(x)=\rm 3\, cm \, \sin(12 \, Hz \ 0{,}25 \, s - 0{,}48 \,\frac{1}{cm} \ x) = 3\, cm \sin( 3 - 0{,}48 \frac{1}{cm} \ x)$$

Es ist sinnvoll sich die Ergebnisse mal mit einem Taschenrechner oder einem Programm zeichnen zu lassen.

Links

• dynamische Arbeitsblätter zur Erarbeitung der Grundbegriffe der Wellenlehre (C. Wolfseher)
• Applet: Phasenzeiger einer Welle (Jörg Bogendörfer Didaktik der Physik Uni Erlangen)

Fußnoten

1. Hochspringen ↑ Zur Vereinfachung beginnt die Zeitmessung ( $$t = 0\,\rm s$$ ) wenn die Auslenkung im Ursprung ( $$x = 0\,\rm m$$ ) gerade Null beträgt und ansteigt.