Aufgaben zur Kinematik (Bewegungslehre) - Lösungen: Unterschied zwischen den Versionen
(→1) Eine Rolltreppe: vertikale statt horizontale Geschwindigkeit) |
|||
| (2 dazwischenliegende Versionen von einem anderen Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | ([[Inhalt_Klasse_10|'''Klassische Mechanik''']] > [[Inhalt_Klasse_10#Kinematik_-_.22Ja.2C_wo_laufen_sie_denn.3F.22|'''Kinematik''']]) | ||
| + | |||
| + | ([[Inhalt_Kursstufe|'''Kursstufe''']] > [[Inhalt_Kursstufe#Mechanik|''' Mechanik''']]) | ||
| + | |||
| + | *[[Aufgaben zur Kinematik (Bewegungslehre)|'''Zurück zu den Aufgaben''']] | ||
| + | |||
==Grundlegendes== | ==Grundlegendes== | ||
[[Image:Mechanik_Koordinatensystem_geradlinig.jpg|thumb]] | [[Image:Mechanik_Koordinatensystem_geradlinig.jpg|thumb]] | ||
| Zeile 216: | Zeile 222: | ||
Auf dem Rückweg fliegt sie mit 1025km/h. Damit benötigt sie für diese Strecke: | Auf dem Rückweg fliegt sie mit 1025km/h. Damit benötigt sie für diese Strecke: | ||
| − | :<math>v = \frac{\Delta s}{\Delta t} \quad \Longleftrightarrow \quad \Delta t = \frac{\Delta s}{v} = \frac{9300\,\rm km}{1025\,\rm km/h} = \mathrm{9{,}07\, h = | + | :<math>v = \frac{\Delta s}{\Delta t} \quad \Longleftrightarrow \quad \Delta t = \frac{\Delta s}{v} = \frac{9300\,\rm km}{1025\,\rm km/h} = \mathrm{9{,}07\, h = 9\, h\ 4\,min }</math> |
[[Datei:Aufgabe_Geschwindigkeit_vektoriell_Flugzeug.png|thumb|453px]] | [[Datei:Aufgabe_Geschwindigkeit_vektoriell_Flugzeug.png|thumb|453px]] | ||
| Zeile 222: | Zeile 228: | ||
:<math> \Delta t = \frac{\Delta s}{v} = \frac{18600\,\rm km}{925\,\rm km/h} = \mathrm{20{,}11\, h = 20\, h\ 6\,min }</math> | :<math> \Delta t = \frac{\Delta s}{v} = \frac{18600\,\rm km}{925\,\rm km/h} = \mathrm{20{,}11\, h = 20\, h\ 6\,min }</math> | ||
| − | Das Flugzeug ist im Vergleich zum Hin- und Rückweg mit Westwind um 14 Minuten schneller! Und | + | Das Flugzeug ist im Vergleich zum Hin- und Rückweg mit Westwind um 14 Minuten schneller! Und das, obwohl man mit Rückenwind 100km/h schneller und mit Gegenwind 100km/h langsamer ist. <br/> Auf dem Hin- und Rückweg ist man aber eine längere Zeit mit Gegenwind als mit Rückenwind unterwegs. Deshalb kann der Rückenwind den Gegenwind nicht wieder "wettmachen". |
'''c)''' Zuerst kann man ausrechnen, wie schnell das Flugzeug bei Windstille sein muss: | '''c)''' Zuerst kann man ausrechnen, wie schnell das Flugzeug bei Windstille sein muss: | ||
:<math>v = \frac{\Delta s}{\Delta t} = \frac{9300\,\rm km}{11,17\,\rm h} = 833\,\rm km/h</math> | :<math>v = \frac{\Delta s}{\Delta t} = \frac{9300\,\rm km}{11,17\,\rm h} = 833\,\rm km/h</math> | ||
Gegen den Wind muss die Boeing also mit 933 km/h relativ zur Luft fliegen und mit Rückenwind nur mit 733 km/h. | Gegen den Wind muss die Boeing also mit 933 km/h relativ zur Luft fliegen und mit Rückenwind nur mit 733 km/h. | ||
Aktuelle Version vom 25. Mai 2017, 06:57 Uhr
(Klassische Mechanik > Kinematik)
Inhaltsverzeichnis
- 1 Grundlegendes
- 2 Bewegungsdiagramme
- 2.1 1) Ein Ortsdiagramm interpretieren
- 2.2 2) Zeichne qualitativ das Ortsdiagramm zu folgender Geschichte:
- 2.3 3) Ein Spaziergang
- 2.4 3) Interpretation eines Geschwindigkeitsdiagramms mit konstanten Geschwindigkeiten
- 2.5 4) Interpretation eines Geschwindigkeitsdiagramms mit ansteigender Gschwindigkeit
- 2.6 5) Eine Fahrt mit dem Fahrrad
- 2.7 6) Bergab rollen
- 3 Vektorielle Geschwindigkeiten
Grundlegendes
- Welche Fragen beantwortet die Kinematik?
- Wann ist ein beobachter Gegenstand wo? Und wie schnell ist er? Es ist die Lehre von der Bewegung.
- Wozu braucht man ein Koordinatensystem?
- Um den Ort eines Gegenstandes mit Hilfe von Zahlen auszudrücken.
- Was versteht man unter [math]\dot s[/math], der momentanen zeitlichen Änderungsrate des Ortes?
- [math]\dot s[/math] ist die Geschwindigkeit
- Warum ist die Geschwindigkeit eine vektorielle Größe, die Masse aber nicht?
- Vektoren werden durch Betrag und Richtung festgelegt. Um eine Geschwindigkeit eindeutig zu bestimmen, benötigt man Betrag und Richtung. Die Masse eines Gegenstandes hat keine Richtung.
- Nenne weitere vektorielle und skalare Größen mit ihren Einheiten.
- vektoriell: Beschleunigung (m/s^2), Kraft (N), Impuls (kg· m/s oder Hy)
- skalar: Masse (kg), Zeit (s),Temperatur (K oder °C), Energie (J oder kWh)
- Bei welchen Bewegungen unterscheidet sich der zurückgelegte Weg von der Änderung des Ortes?
- Läuft eine Person einen Halbkreis auf dem Boden, so ist die gesamte Änderung des Ortes gerade der Durchmesser des Kreises. Der zurückgelegte Weg ist aber der halbe Umfang und somit länger, die Person ist ja auch einen Umweg gelaufen.
- Läuft die Person sogar einmal im Kreis, so gibt es gar keine Ortsänderung aber natürlich einen zurückgelegten Weg.
- Auch wenn eine Person auf einer geraden Linie zunächst nach rechts und dann wieder zurück läuft, ist die Änderung des Ortes viel kleiner als der zurückgelegte Weg.
- Wie kann man die momentante und wie die Durchschnittsgeschwindigkeit an einem s-t-Diagramm ablesen?
- Momentangeschwindigkeit: Ableitung/Steigung - Durchschnittsgeschwindigkeit: Sekante
- Wie kann man die Änderung des Ortes (meistens der zurückgelegte Weg) an einem v-t-Diagramm ablesen?
- Die Fläche zwischen der t-Achse und dem Schaubild der Funktion ergibt die Änderung des Ortes.
Bewegungsdiagramme
1) Ein Ortsdiagramm interpretieren
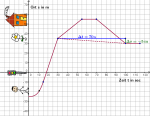
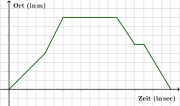
a) Elisabeth steht zunächst 25m vor der Ampel. Dann läuft sie los und wird immer schneller bis sie nach 15sec eine konstante Geschwindigkeit beibehält. Sie läuft an der Ampel vorbei bis zu einer Blume. Nach der Blume geht sie langsamer als vorher auf ein Haus zu, welches sie nach 55sec erreicht. Sie macht dort 15sec Pause und geht dann wieder zurück in Richtung Ampel. Sie passiert noch die Blume und bleibt 5m hinter der Blume stehen.
b) Um die mittlere Geschwindigkeit in den Zeitabschnitten zu bestimmen, berechnet man den Quotienten aus Ortsveränderung und Zeitdauer:
- [math]\bar v = \frac{\Delta s}{\Delta t}[/math]
Eine mittlere Geschwindigkeit von -0,07m/s bedeutet: In der Zeit zwischen 30s und 100s ist Elisabeth pro Sekunde im Mittel 7cm entgegen der Koordinatenrichtung gelaufen.
c) Wie schnell ist sie zum Zeitpunkt [math]t = 10 \, \rm sec[/math]?Dazu zeichnet man die Tangente nach Augenmaß ein und bestimmt mit einem Steigungsdreieck die Geschwindigkeit:
[math] v = \frac{32\,\rm m}{24,\rm s}=1{,}33\,\rm m/s[/math]
2) Zeichne qualitativ das Ortsdiagramm zu folgender Geschichte:
- Elisabeth muss zur Post. Sie schwingt sich auf ihr Rad und fährt gemütlich mit konstanter Geschwindigkeit. Pfeifend genießt sie das schöne Herbstwetter.
- Nach einem Blick auf die Uhr stellt sie erschrocken fest, dass die Post gleich schließt. Deshalb fährt sie jetzt so schnell sie kann (gleichförmig) weiter und schafft es zum Glück gerade noch. In der Post sind noch viele andere Leute und so dauert es eine Weile, bis sie ihren Heimweg antreten kann.
- Sie fährt den gesamten Rückweg mit konstanter Geschwindigkeit und hält nur einmal kurz an, um ihrem Liebsten eine Blume zu pflücken. Die Rückfahrt dauert ungefähr genauso lange wie die Hinfahrt.
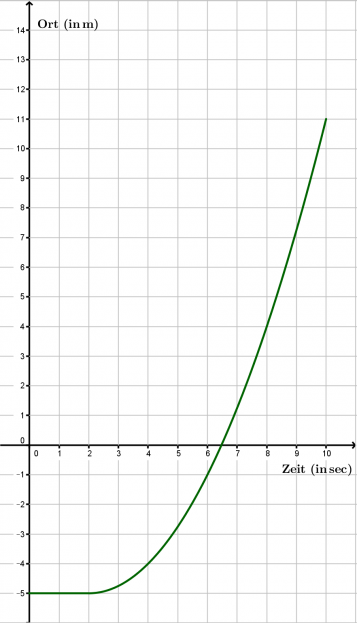
3) Ein Spaziergang
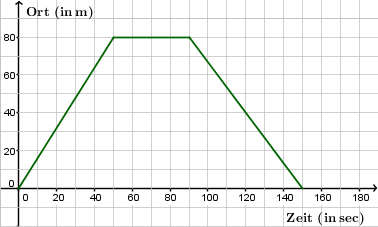
Das ist das Zeit-Ort-Diagramm einer FußgängerIn:
- a) Beschreibe die Bewegung in Worten.
- Sie läuft mit einer konstanten Geschwindigkeit 80m in 45sec. Dann bleibt sie für 40sec stehen, kehrt um und läuft die 80m in einer Minute wieder zurück.
- b) Wie schnell war sie im Durchschnitt in der ersten Minute?
- [math]\bar v = \frac{80\,\rm m}{60\,\rm s}=1{,}33\,\rm m/s[/math]
Und wie schnell bei t = 20 s, t= 60 s und t = 95 s?.
- [math]v(20\,\rm s)= \frac{80\,\rm m}{50\,\rm s}=1{,}6\,\rm m/s[/math]
- [math]v(60\,\rm s)= 0\,\rm m/s[/math]
- [math]v(95\,\rm s)= \frac{-80\,\rm m}{60\,\rm s}=-1{,}33\,\rm m/s[/math]
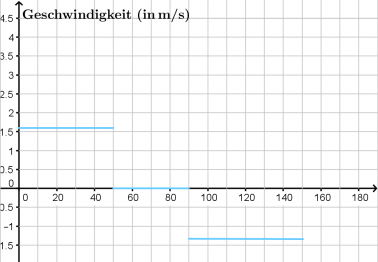
- c) Zeichne das zugehörige t-v-Diagramm.
Zu den Zeitpunkten [math]t=50\,\rm s[/math] und [math]t=90\,\rm s[/math] kann man keine Geschwindigkeit ermitteln und die Geschwindigkeit macht einen Sprung, weil das Ortsdiagramm einen Knick hat. Bei einer realen Bewegung kann das nicht vorkommen, bei dieser vereinfachten Beschreibung aber schon.
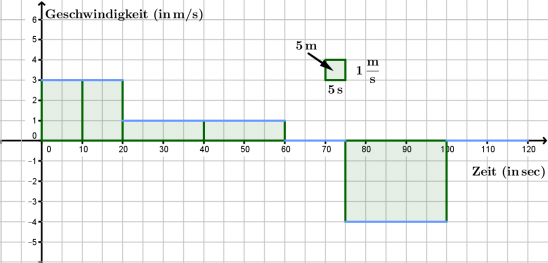
3) Interpretation eines Geschwindigkeitsdiagramms mit konstanten Geschwindigkeiten
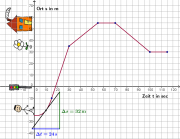
Zum Zeitpunkt t = 0s befindet sich Franz noch 10 Meter vor der Ampel. Ab jetzt wird seine Geschwindigkeit gemessen.
- a) Welche Strecke legt er in der Zeit von t = 20s bis t = 60s zurück?
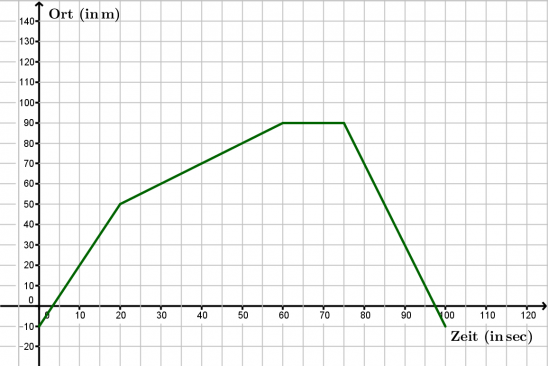
- b) Wo ist Franz nach 20 Sekunden, nach 60 Sekunden, nach 75 Sekunden und nach 100 Sekunden? Erstelle daraus das Ortsdiagramm.
- Zuerst berechnet man die zurückgelegten Strecken in den einzelnen Zeitabschnitten:
- Von 0s bis 20s: [math]\mathrm{\Delta s = 3\frac{m}{s} \cdot 20\, s = 60\, m }[/math]
- Von 20s bis 60s: [math]\mathrm{\Delta s = 1\frac{m}{s} \cdot 40\, s = 40\, m }[/math]
- Von 60s bis 75s: [math]\mathrm{\Delta s = 0\, m }[/math]
- Von 75s bis 100s: [math]\mathrm{\Delta s = -4\frac{m}{s} \cdot 25\, s = -100\, m }[/math]
- In der Zeit von 75s bis 100s ist die Geschwindigkeit negativ, Franz läuft wieder zurück.
- Ausgehend von Franz' Startpunkt 10m vor der Ampel kann man dann seine Position bestimmen. (siehe Ortsdiagramm)
- c) Welche Strecke legt er in der Zeit von t = 10s bis t = 40s zurück?
- [math]\mathrm{\Delta s = 3\frac{m}{s} \cdot 10\, s + 1\frac{m}{s} \cdot 20\, s = 30\, m + 10\,m = 40\,m}[/math]
- d) Löse nun nochmal Aufgabe a) bis c), indem du die jeweilige Rechteckfläche bestimmst!
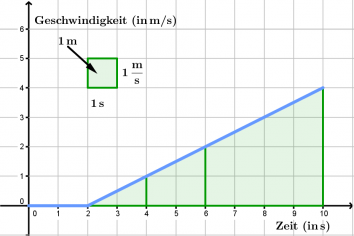
4) Interpretation eines Geschwindigkeitsdiagramms mit ansteigender Gschwindigkeit
Ein Fahrrad steht 5m vor einer roten Ampel. Nachdem sie grün geworden ist, fährt es los und beschleunigt, wird also immer schneller. Auch hier kann man aus dem t-v-Diagramm ablesen, wie weit das Rad in einer Zeitspanne fährt. Denn auch hier läßt sich die Fläche unter dem Schaubild als zurückgelegte Wegstrecke interpretieren! Dazu muss man in diesem Fall die Fläche von Dreiecken berechnen oder wieder Kästchen zählen.
- a) Wo ist das Fahrrad nach 2 Sekunden?
- Da es noch immer steht, ist es noch 5m vor der Ampel.
- b) Welche Strecke legt es ungefähr in der Zeit von t = 2s bis t = 4s zurück? (Benutze die Durchschnittsgeschwindigkeit.)
- [math]\mathrm{\Delta s = \frac{1}{2} \cdot 1\frac{m}{s} \cdot 2\, s = 0{,}5 \frac{m}{s} \cdot 2\, s = 1\, m }[/math]
- Hat es bei t = 4s die Ampel schon erreicht?
- Nein, es steht noch 4m vor der Ampel.
- c) Legt das Fahrrad von t=4s bis t=6s eine größere oder eine kleinere Strecke als zwischen t=2s und 4s zurück?
- Die mittlere Geschwindigkeit innerhalb dieser 2s ist größer, daher legt es eine größere Strecke zurück.
- Welche Strecke legt es zurück und wo ist es bei t = 6s?
- Man kann entweder die mittlere Geschwindigkeit benutzen oder die Fläche berechnen:
- [math]\mathrm{\Delta s = 1{,}5 \frac{m}{s} \cdot 2\, s = 3\, m }[/math]
- d) Bestimme, welche Strecke das Rad von t = 2s bis t = 10s zurückgelegt hat. Wieviel Meter hinter der Ampel ist es zum Zeitpunkt t =10s?
- [math]\mathrm{\Delta s = \frac{1}{2} \cdot 4 \frac{m}{s} \cdot 8\, s = 16\, m }[/math]
- Deshalb steht es nach 10 Sekunden 11 Meter hinter der Ampel.
- e) Zeichne das Ortsdiagramm der Fahrradfahrt.
5) Eine Fahrt mit dem Fahrrad
Eine RadfahrerIn fährt mit konstanter Beschleunigung los und erreicht nach 10 Sekunden eine Geschwindigkeit von 18 km/h. Sie fährt nun eine Minute lang mit dieser Geschwindigkeit. Dann muss sie an einer roten Ampel bremsen. Weil sie gute Bremsen hat, braucht sie nur 2,5 Sekunden um anzuhalten.
- a) Zeichne ein t-v-Diagramm der Fahrt.
- Zunächst ist es sinnvoll die Geschwindigkeit in m/s umzurechnen:
- [math]\mathrm{18\frac{km}{h}=18\frac{1000\,m}{3600\,s}=5\frac{m}{s}}[/math]
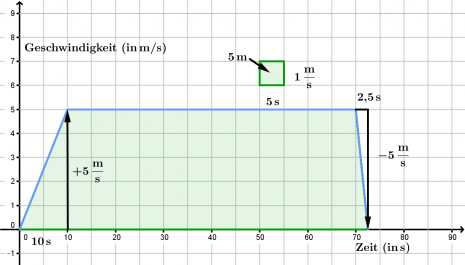
- b) Wie groß ist die Beschleunigung, mit der sie beschleunigt und die, mit der sie bremst?:
- [math]a=\frac{\Delta v}{\Delta t}=\mathrm{\frac{5\frac{m}{s}}{\Delta 10\,s}=0{,}5\frac{m}{s^2}}[/math]
- c) Wie lange dauert die Fahrt und welche Strecke legt sie dabei zurück?.
- Die Fahrt dauert 1min 12,5s.
- Die zurückgelegte Strecke bestimmt man als Fläche im v-t-Diagramm:
- [math]\begin{array}{rclclcl} \Delta s &=& \mathrm{\frac{1}{2}\cdot 5\frac{m}{s}\cdot 10\,s} &+& \mathrm{5\frac{m}{s}\cdot 60\,s} &+& \mathrm{\frac{1}{2}\cdot 5\frac{m}{s}\cdot 2{,}5\,s}\\ &=& \mathrm{25\,m} &+& \mathrm{300\,m} &+& \mathrm{\ 6{,}25\,m}\\ &=& \mathrm{331{,}25\,m} \end{array}[/math]
- Für das Beschleunigen benötigt sie also eine Strecke von 25m, dann legt sie 300m mit konstanter Geschwindigkeit zurück und hat einen Bremsweg von 2,5m.
6) Bergab rollen
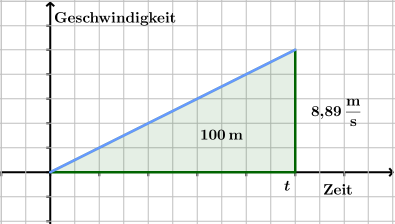
Ein Radfahrer erreicht an einem Gefälle bei konstanter Beschleunigung aus der Ruhe nach 100 m eine Geschwindigkeit von 32 km/h. Wieviel Zeit ist dabei vergangen? (Hinweis. Ein v-t-Diagramm skizzieren, in kompatible Einheiten umrechnen.)
Zuerst rechnet man die Geschwindigkeit in m/s um:
- [math]\mathrm{32\frac{km}{h}=32\frac{100\,m}{3600\,s}=8{,}89\,\frac{m}{s}}[/math]
Das Geschwindigkeitsdiagramm kann man ohne die Zeitangabe nur ohne Einheiten zeichnen:
Die Fläche des Dreiecks muss den zurückgelegten 100m entsprechen:
- [math] \begin{array}{rrcll} & \mathrm{\frac{1}{2} \cdot 8{,}89\,\frac{m}{s}} \cdot t & = & 100\,\rm m & | \cdot 2 \ |\, \mathopen: 8{,}89\,\frac{\rm m}{\rm s} \\ \Rightarrow & t & = & 22{,}5\,\rm s \end{array} [/math]
Das Fahrrad ist also 22,5 Sekunden lang gerollt!
Vektorielle Geschwindigkeiten
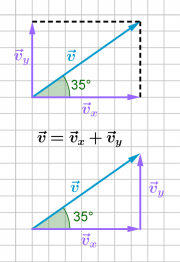
1) Eine Rolltreppe
a) Die horizontale und die vertikale Geschwindigkeitskomponente stehen senkrecht aufeinander. Sie bilden mit dem Geschwindigkeitsvektor ein rechtwinkliges Dreieck. Für die Komponenten gilt daher:
- [math]\cos 35^\circ = \frac{v_x}{v}[/math]
- [math]\sin 35^\circ = \frac{v_y}{v}[/math]
Woraus folgt:
- [math]v_x = \cos 35^\circ \cdot v = 0{,}82 \cdot 80\,\rm \frac{cm}{s} = 66\,\rm \frac{cm}{s}[/math]
- [math]v_y = \sin 35^\circ \cdot v = 0{,}57 \cdot 80\,\rm \frac{cm}{s} = 46\,\rm \frac{cm}{s}[/math]
b) Alexander steigt in der Sekunde um 66 cm an, also braucht er 23s um die 15 Höhenmeter zu überwinden:
- [math]v_x = \frac{\Delta s}{\Delta t} \quad \Longleftrightarrow \quad 0{,}66\,\rm \frac{m}{s} = \frac{15\,\rm m}{\Delta t}[/math]
Nach der Zeit aufgelöst:
- [math]\Delta t = \frac{15\,\rm m}{0{,}46\,\rm \frac{m}{s}} = 32{,}6\,\rm s[/math]
Oder man berechnet den schrägen Weg, also die Länge der Rolltreppe, den er mit 80cm/s zurücklegt.
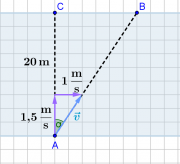
2) Über den Fluss
Wenn Eva senkrecht zur Wasserströmung paddelt, setzt sich ihre Geschwindigkeit relativ zum Ufer aus zwei zueinander senkrecht stehenden Komponenten zusammen.
a) Mit dem Satz des Pythagoras ergibt sich ihre Geschwindigkeit zu:
- [math]v^2 = \left( 1\,\rm \frac{m}{s}\right)^2 + \left( 1{,}5\,\rm\frac{m}{s} \right)^2 =[/math]
- [math]v= \sqrt{\left( 1\,\rm \frac{m}{s}\right)^2 + \left( 1{,}5\,\rm\frac{m}{s} \right)^2} = \sqrt{3{,}25\,\rm\frac{m^2}{s^2}} = 1{,}8 \,\rm\frac{m}{s}[/math]
b) Evas Geschwindigkeit quer zur Wasserströmung beträgt 1,5m/s. Daher braucht sie ca. 13s für die 20m bis zum anderen Ufer:
- [math]v_y = \frac{\Delta s}{\Delta t} \quad \Longleftrightarrow \quad 1{,}5\,\rm \frac{m}{s} = \frac{20\,\rm m}{\Delta t}[/math]
Nach der Zeit aufgelöst ergibt sich:
- [math]\Delta t = \frac{20\,\rm m}{1{,}5\,\rm \frac{m}{s}} = 13{,}3\,\rm s[/math]
c) Da sie 13,3s unterwegs ist und in jeder Sekunde 1m abgetrieben wird, wird sie insgesamt um 13,3m abgetrieben:
- [math]v_x = \frac{\Delta s}{\Delta t} \quad \Longleftrightarrow \quad 1\,\rm \frac{m}{s} = \frac{\Delta s}{13{,}3\,\rm s}[/math]
Nach der Strecke aufgelöst ergibt sich:
- [math]\Delta s = v\, \Delta t = 1\,\rm \frac{m}{s} \cdot 13{,}3\,\rm s = 13{,}3\,\rm m[/math]
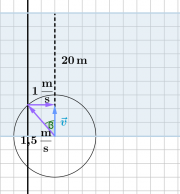
d) Eva muss so schräg fahren, dass die Summe ihrer Geschwindigkeit relativ zum Wasser und der Strömungsgeschwindigkeit senkrecht zur Wasserströmung ist. (Dazu muss ihre Geschwindigkeitskomponente gegen die Wasserströmung gerade 1m/s betragen.)
Daraus ergibt sich für den Winkel [math]\beta[/math]:
- [math]\sin \beta = \frac{1\,\rm \frac{m}{s}}{1{,}5\,\rm\frac{m}{s}} = 0{,}666[/math]
- [math]\beta =42^\circ[/math]
Eva muss also um 42° von dem direkten Kurs abweichen.
e) Um die Fahrtdauer zu bestimmen, muss man die Geschwindigkeit v kennen. Wieder hilft der Satz des Pythagoras:
- [math]\left(1{,}5\,\rm\frac{m}{s}\right)^2 = \left(1\,\rm\frac{m}{s}\right)^2 + v^2[/math]
Nach der Geschwindigkeit v auflösen:
- [math]v = \sqrt{\left(1{,}5\,\rm\frac{m}{s}\right)^2 - \left(1\,\rm\frac{m}{s}\right)^2} =\sqrt{1{,}25\,\rm\frac{m^2}{s^2}} \approx 1{,}12\,\rm\frac{m}{s} [/math]
Nun kann man die Zeit berechnen:
- [math]\Delta t = \frac{20\,\rm m}{1{,}12\,\rm \frac{m}{s}} = 18\,\rm s[/math]
Eva ist also 2s länger unterwegs als auf dem Hinweg.
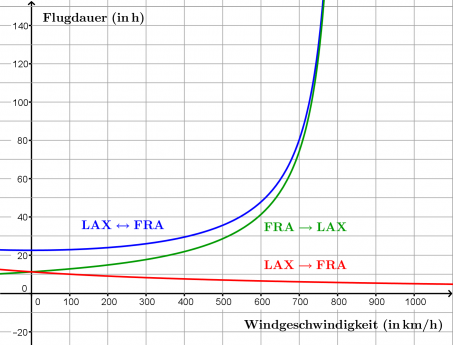
3) Über den Atlantik fliegen
a) Von Frankfurt nach Los Angeles fliegt die Boeing mit einer Geschwindigkeit von nur 825 km/h relativ zum Erdboden. Damit benötigt sie für diese Strecke:
- [math]v = \frac{\Delta s}{\Delta t} \quad \Longleftrightarrow \quad \Delta t = \frac{\Delta s}{v} = \frac{9300\,\rm km}{825\,\rm km/h} = \mathrm{11{,}27\, h = 11\, h\ 16\,min }[/math]
Auf dem Rückweg fliegt sie mit 1025km/h. Damit benötigt sie für diese Strecke:
- [math]v = \frac{\Delta s}{\Delta t} \quad \Longleftrightarrow \quad \Delta t = \frac{\Delta s}{v} = \frac{9300\,\rm km}{1025\,\rm km/h} = \mathrm{9{,}07\, h = 9\, h\ 4\,min }[/math]
b) Bei Windstille beträgt die Entfernung hin und zurück 18600 km und die Geschwindigkeit beträgt 925 km/h:
- [math] \Delta t = \frac{\Delta s}{v} = \frac{18600\,\rm km}{925\,\rm km/h} = \mathrm{20{,}11\, h = 20\, h\ 6\,min }[/math]
Das Flugzeug ist im Vergleich zum Hin- und Rückweg mit Westwind um 14 Minuten schneller! Und das, obwohl man mit Rückenwind 100km/h schneller und mit Gegenwind 100km/h langsamer ist.
Auf dem Hin- und Rückweg ist man aber eine längere Zeit mit Gegenwind als mit Rückenwind unterwegs. Deshalb kann der Rückenwind den Gegenwind nicht wieder "wettmachen".
c) Zuerst kann man ausrechnen, wie schnell das Flugzeug bei Windstille sein muss:
- [math]v = \frac{\Delta s}{\Delta t} = \frac{9300\,\rm km}{11,17\,\rm h} = 833\,\rm km/h[/math]
Gegen den Wind muss die Boeing also mit 933 km/h relativ zur Luft fliegen und mit Rückenwind nur mit 733 km/h.