Kraft und Energie: Unterschied zwischen den Versionen
(→Energiemengen im Weg-Kraft-Diagramm) |
|||
| (6 dazwischenliegende Versionen des gleichen Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | ([[Inhalt_Kursstufe|'''Kursstufe''']] > [[Inhalt_Kursstufe#Mechanik|''' Mechanik''']]) | ||
| + | ([[Inhalt_Klasse_10|'''Klassische Mechanik''']] > [[Inhalt_Klasse_10#Energieerhaltung|'''Energieerhaltung''']]) | ||
| Zeile 6: | Zeile 8: | ||
| − | [[Image: | + | [[Image:Mechanik_E=Fs_Beschleunigen.jpg|thumb|none]] |
| − | + | Das Männchen übt eine Kraft F in Richtung des Weges s auf den Wagen aus. Dabei wird die Energie <math>E=F\, s</math> vom Männchen auf den Wagen übertragen. Das kann man daran sehen, dass der Wagen schneller wird. Der Wagen erhält kinetische Energie (Bewegungsenergie). <br style="clear: both" /> | |
| − | + | [[Image:Mechanik_E=Fs_Bremsen.jpg|thumb|none]] | |
| − | [[Image: | + | In diesem Fall übt das Männchen eine Kraft aus, die der Bewegungsrichtung des Wagens entgegengesetzt ist. Dabei rutscht es über den Boden. Der Wagen verliert bei diesem Vorgang seine kinetische Energie <math>E=F\, s</math> und diese wird durch die Reibung des Männchens mit dem Untergrund in Wärmeenergie umgewandelt (auf Entropie umgeladen). <br style="clear: both" /> |
| + | [[Image:Mechanik_E=Fs_Gleichgewicht.jpg|thumb|none]] | ||
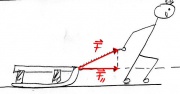
| − | + | Das Männchen zieht den Schlitten mit konstanter Geschwindigkeit. Wegen der Reibung ist dazu eine Kraft nötig! | |
| − | + | Die Kraft in Richtung der Bewegung überträgt also die Energie in die Bewegung des Schlittens und die gleichgroße Reibungskraft sorgt dafür, dass die Energie <math>E=F\, s</math> gleich wieder von der Bewegung auf die Wärme der Kufen und des Schnees übertragen wird. | |
| + | <br style="clear: both" /> | ||
| − | [[Image: | + | [[Image:Mechanik_E=Fs_schräg_Drachen.jpg|thumb|none]] |
| − | + | Hier übt das Männchen eine Kraft (F) auf den Drachen aus. Da diese jedoch schräg zur Bewegungsrichtung des Drachens gerichtet ist, wirkt von dieser Kraft effektiv nur die parallel gerichtetete Kraft <math>F_{||}</math> auf den Drachen. Es wird also nur Energie in der Höhe von <math>E=F_{||}\, s</math> übertragen. | |
| − | [[Image: | + | [[Image:Mechanik_E=Fs_schräg_Schlitten.jpg|thumb|none]] |
| − | + | Dieses Beispiel ähnelt dem Beispiel mit dem Drachen, denn auch hier übt das Männchen eine schräg gerichtete Kraft aus. Wir müssen also auch hier wieder die parallel zur Bewegungsrichtung des Schlittens gerichtete Kraft <math>F_{||}</math> betrachten um herauszufinden, wieviel Energie übertragen wird. | |
| − | + | [[Image:Mechanik_E=Fs_Sonne_Erde.jpg|thumb|none]] | |
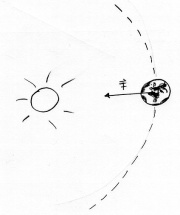
| − | + | Ein klassisches Beispiel für eine Kreisbewegung: Die Erde dreht sich um die Sonne, wobei die Zentripetalkraft immer senkrecht auf der Bewegungsrichtung ist. Es wird also keine Energie übertragen, sondern lediglich die Bewegungsrichtung verändert. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | Ein klassisches Beispiel für eine Kreisbewegung: Die Erde dreht sich um die Sonne, wobei die Zentripetalkraft immer senkrecht auf der Bewegungsrichtung ist. Es wird also keine Energie übertragen, sondern lediglich die Bewegungsrichtung verändert. | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| + | == Energiemengen im Kraft-Weg-Diagramm == | ||
| + | <gallery widths=180px heights=120px perrow=4> | ||
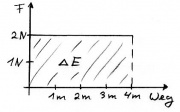
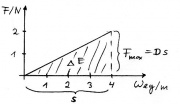
| + | Bild:Mechanik_sF_Diagramm.jpg|Bei einer konstanten Kraft in Richtung des Weges entspricht die Energiezunahme <math>\Delta E = F \cdot s </math> der rechteckigen Fläche unter dem Graphen. | ||
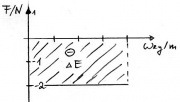
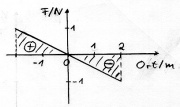
| + | Bild:Mechanik_sF_Diagramm_negativ.jpg|Wirkt die Kraft gegen die Bewegungsrichtung, so wird die Fläche negativ gewertet. Die Enegiemenge sinkt um <math>\Delta E</math>. | ||
| + | Bild:Mechanik_sF_Diagramm_Feder.jpg|Dehnt man eine Feder, so nimmt die Kraft proportional zum Weg zu. Die hineingesteckte Energiemenge entspricht einer Dreiecksfläche. | ||
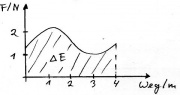
| + | Bild:Mechanik_sF_Diagramm_variabel.jpg|Auch bei einer veränderlichen Kraft berechnet man die übertragene Energiemenge als Fläche unter dem Graphen. | ||
| + | Bild:Mechanik_E=Fs_Pendel.jpg|Bei dieser Federschwingung bekommt das Pendel am Anfang Energie,... | ||
| + | Bild:Mechanik_sF_Diagramm_Federpendel.jpg|...um sie nach dem Durchgang durch die Ruhelage wieder abzugeben. | ||
| + | </gallery> | ||
== Formeln für Energieformen == | == Formeln für Energieformen == | ||
| Zeile 80: | Zeile 54: | ||
== Energiebilanzen == | == Energiebilanzen == | ||
* Es gilt, wie überall die Energieerhaltung | * Es gilt, wie überall die Energieerhaltung | ||
| − | + | * Energiebilanzen Achterbahn, Pendel, etc | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | *Energiebilanzen Achterbahn, Pendel, etc | + | |
Aktuelle Version vom 26. Mai 2017, 10:02 Uhr
(Klassische Mechanik > Energieerhaltung)
Inhaltsverzeichnis
Energieübertragung mit Kräften
Wirkt eine Kraft parallel längs eines Weges, so wird Energie übertragen. Ist die Kraft senkrecht auf dem Weg, so nicht, es wird lediglich die Richtung geändert (Kreisbewegung). Ist sie schräg, wirkt nur die parallele Komponente. Wirkt eine Kraft ohne Bewegung, so wird keine Energie übertragen. (Halten von schweren Gegenständen und menschliche Muskeln?!)
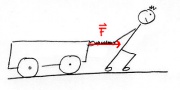
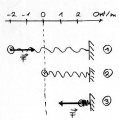
Das Männchen übt eine Kraft F in Richtung des Weges s auf den Wagen aus. Dabei wird die Energie [math]E=F\, s[/math] vom Männchen auf den Wagen übertragen. Das kann man daran sehen, dass der Wagen schneller wird. Der Wagen erhält kinetische Energie (Bewegungsenergie).
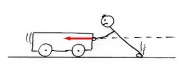
In diesem Fall übt das Männchen eine Kraft aus, die der Bewegungsrichtung des Wagens entgegengesetzt ist. Dabei rutscht es über den Boden. Der Wagen verliert bei diesem Vorgang seine kinetische Energie [math]E=F\, s[/math] und diese wird durch die Reibung des Männchens mit dem Untergrund in Wärmeenergie umgewandelt (auf Entropie umgeladen).
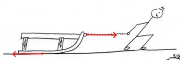
Das Männchen zieht den Schlitten mit konstanter Geschwindigkeit. Wegen der Reibung ist dazu eine Kraft nötig!
Die Kraft in Richtung der Bewegung überträgt also die Energie in die Bewegung des Schlittens und die gleichgroße Reibungskraft sorgt dafür, dass die Energie [math]E=F\, s[/math] gleich wieder von der Bewegung auf die Wärme der Kufen und des Schnees übertragen wird.
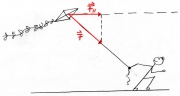
Hier übt das Männchen eine Kraft (F) auf den Drachen aus. Da diese jedoch schräg zur Bewegungsrichtung des Drachens gerichtet ist, wirkt von dieser Kraft effektiv nur die parallel gerichtetete Kraft [math]F_{||}[/math] auf den Drachen. Es wird also nur Energie in der Höhe von [math]E=F_{||}\, s[/math] übertragen.
Dieses Beispiel ähnelt dem Beispiel mit dem Drachen, denn auch hier übt das Männchen eine schräg gerichtete Kraft aus. Wir müssen also auch hier wieder die parallel zur Bewegungsrichtung des Schlittens gerichtete Kraft [math]F_{||}[/math] betrachten um herauszufinden, wieviel Energie übertragen wird.
Ein klassisches Beispiel für eine Kreisbewegung: Die Erde dreht sich um die Sonne, wobei die Zentripetalkraft immer senkrecht auf der Bewegungsrichtung ist. Es wird also keine Energie übertragen, sondern lediglich die Bewegungsrichtung verändert.
Energiemengen im Kraft-Weg-Diagramm
Bei einer konstanten Kraft in Richtung des Weges entspricht die Energiezunahme [math]\Delta E = F \cdot s [/math] der rechteckigen Fläche unter dem Graphen.
Wirkt die Kraft gegen die Bewegungsrichtung, so wird die Fläche negativ gewertet. Die Enegiemenge sinkt um [math]\Delta E[/math].
Dehnt man eine Feder, so nimmt die Kraft proportional zum Weg zu. Die hineingesteckte Energiemenge entspricht einer Dreiecksfläche.
Auch bei einer veränderlichen Kraft berechnet man die übertragene Energiemenge als Fläche unter dem Graphen.
Bei dieser Federschwingung bekommt das Pendel am Anfang Energie,...
...um sie nach dem Durchgang durch die Ruhelage wieder abzugeben.
Formeln für Energieformen
Lageenergie, Bewegungsenergie, Spannenergie
E=mgh E=1/2mv^2 E=1/2Ds^2
Energiebilanzen
- Es gilt, wie überall die Energieerhaltung
- Energiebilanzen Achterbahn, Pendel, etc
