Aufgaben zur Impulserhaltung: Unterschied zwischen den Versionen
K (→Elfmeter) |
|||
| (19 dazwischenliegende Versionen des gleichen Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | ([[Inhalt_Klasse_10|'''Klassische Mechanik''']] > [[Inhalt_Klasse_10#Impulserhaltung|'''Impulserhaltung''']]) | ||
| + | |||
| + | ([[Inhalt_Kursstufe|'''Kursstufe''']] > [[Inhalt_Kursstufe#Mechanik|''' Mechanik''']]) | ||
| + | |||
===Ein Ruderboot=== | ===Ein Ruderboot=== | ||
| − | [[ | + | [[Bild:Vierer mit Steuermann.jpg|thumb|Vierer mit Steuermann]] |
Beschreibe mit Hilfe des Impulses, wie das Ruderboot losfährt und warum es ohne zu Rudern wieder langsamer wird. | Beschreibe mit Hilfe des Impulses, wie das Ruderboot losfährt und warum es ohne zu Rudern wieder langsamer wird. | ||
| + | <br style="clear: both" /> | ||
| + | |||
| + | ===Raumstation Mir=== | ||
| + | Im Europapark ist ein Trainingsmodul der ehemaligen russischen Raumstation Mir zu besichtigen. Dabei fallen unter anderem kleine Düsen ins Auge, die zur Lagekorrektur gedacht sind. | ||
| + | |||
| + | *Wie kann man mit den Steuerdüsen die Mir drehen oder verschieben? | ||
| + | :Mache dazu eine Zeichnung und zeichne auch die Lage und Richtung der Düsen ein. | ||
| + | *Wieviele Steuerdüsen braucht man, um die Raumstation in alle beliebigen Richtung zu drehen oder zu verschieben? | ||
| + | *Zusätzlich hatte die Mir noch [[Drehimpulserhaltung#Lagekorrektur von Raumstationen und Satelliten|Kreisel zur Stabilisierung und Steuerung]]. | ||
| + | <gallery widths=150px heights=150px perrow=4 > | ||
| + | Bild:Mir_Space_Shuttle.jpg|Mir mit Space Shuttle Atlantis | ||
| + | Bild:Mir_12_Juni_1998.jpg|Mir in höherer Auflösung | ||
| + | Bild:Impulserhaltung_Mir_mit_Steuerdüsen_Europapark.jpg|Trainigsmodul im Europapark | ||
| + | Bild:Mir_Europapark_Steuerdüsen.jpg|Steuerdüsen eines Moduls | ||
| + | </gallery> | ||
| + | |||
| + | ===Astronaut in der ISS=== | ||
| + | Astronauten in der ISS bewegen sich fort, indem sie sich an den Wänden der Raumstation abdrücken. | ||
| + | Alexander Gerst drückt sich mit einem kräftigen Schubs von der Bordwand ab und erreicht so eine Geschwindigkeit von 1 m/s. | ||
| + | *Mit welcher Geschwindigkeit bewegt sich durch das Abdrücken nun die ISS? Schätze notwendige Daten ab oder recherchiere im Netz. | ||
| + | |||
| + | ===Die Welt bewegen=== | ||
| + | Können Menschen die ganze Erde in Bewegung versetzen? Vielleicht, wenn sämtliche Einwohner Chinas mitmachen! Sie springen gleichzeitig zusammen nach oben. Dabei springen sie mit ca. 2,5m/s ab. (Damit erreichen sie eine Höhe von 30cm.) | ||
| + | *Welche Bewegung führt die Erde während des Sprungs aus? | ||
| + | |||
| + | Ein Mensch hat eine Masse von ca. 50kg, es gibt ca. 7 Millierden Einwohner in China und die Erde hat eine Masse von ca. <math>6 \cdot 10^{24}\,\rm kg</math>. | ||
| + | *Wie schnell wird die Erde durch den Sprung? Berechne die Geschwindigkeit in m/s und in Meter pro Jahr! | ||
===Elfmeter=== | ===Elfmeter=== | ||
| Zeile 7: | Zeile 38: | ||
Bei einem Elfmeter hält der Torwart den Ball während er springt, also keinen Kontakt zum Boden hat. | Bei einem Elfmeter hält der Torwart den Ball während er springt, also keinen Kontakt zum Boden hat. | ||
| − | *Warum wird er dadurch ein wenig in Richtung | + | *Warum wird er dadurch ein wenig in Richtung des Tors beschleunigt? |
*Welche Angaben benötigt man, um die Impulsmenge des Balles zu bestimmen? Bestimme die Impulsmenge mit den geschätzten Werten. | *Welche Angaben benötigt man, um die Impulsmenge des Balles zu bestimmen? Bestimme die Impulsmenge mit den geschätzten Werten. | ||
| Zeile 14: | Zeile 45: | ||
*Mit welcher Geschwindigkeit bewegt sich nach dem Festhalten der Torwart auf die Torlinie zu? | *Mit welcher Geschwindigkeit bewegt sich nach dem Festhalten der Torwart auf die Torlinie zu? | ||
*Wie stark sind beim Fangen die Kräfte auf den Ball und den Torwart ? | *Wie stark sind beim Fangen die Kräfte auf den Ball und den Torwart ? | ||
| + | <br style="clear: both" /> | ||
| − | === | + | ===Billard I=== |
| + | [[Datei:Aufgaben_Impuls_Billiard_I.jpg|thumb|264px]] | ||
Beim Billiardspielen wird eine Kugel senkrecht zur Bande gespielt. Von Reibungsverlusten abgesehen prallt sie mit genau dem entgegengesetzten Impuls wieder zurück. | Beim Billiardspielen wird eine Kugel senkrecht zur Bande gespielt. Von Reibungsverlusten abgesehen prallt sie mit genau dem entgegengesetzten Impuls wieder zurück. | ||
Stellt man nun eine Impulsbilanz auf, so stellt man fest, dass die Summe der Impulse nicht gleich geblieben ist. Es fehlt die Impulsmenge <math>2\vec p</math>! | Stellt man nun eine Impulsbilanz auf, so stellt man fest, dass die Summe der Impulse nicht gleich geblieben ist. Es fehlt die Impulsmenge <math>2\vec p</math>! | ||
*Wo ist der fehlende Impuls? | *Wo ist der fehlende Impuls? | ||
| + | <br style="clear: both" /> | ||
===Ein Segelboot=== | ===Ein Segelboot=== | ||
| Zeile 25: | Zeile 59: | ||
Ein Segelboot hat den Spinnaker gesetzt. Dadurch wird der Rückenwind gebremst. | Ein Segelboot hat den Spinnaker gesetzt. Dadurch wird der Rückenwind gebremst. | ||
*Beschreibe, wie sich dadurch der Impuls der Luft und des Bootes ändert. | *Beschreibe, wie sich dadurch der Impuls der Luft und des Bootes ändert. | ||
| − | *Um die Geschwindigkeit des Bootes | + | *Um die Geschwindigkeit des Bootes 10 Sekunden nach dem Start abzuschätzen, benötigt man die Masse des Bootes mit 2000kg und die Segelfläche von 50 m^2. Außerdem muss man wissen, dass ein Liter Luft eine Masse von ca. 1 Gramm hat. Der Wind pustet mit 5 m/sec und wird auf 1 m/sec abgebremst. |
:Rechenweg: >Luftvolumen >Luftmasse >Luftimpuls >Änderung des Luftimpulses >Bootimpuls >Bootgeschwindigkeit. | :Rechenweg: >Luftvolumen >Luftmasse >Luftimpuls >Änderung des Luftimpulses >Bootimpuls >Bootgeschwindigkeit. | ||
| + | |||
*Warum ist die real erreichte Geschwindigkeit des Bootes bestimmt geringer? | *Warum ist die real erreichte Geschwindigkeit des Bootes bestimmt geringer? | ||
| + | <br style="clear: both" /> | ||
| − | === | + | ===Billard II=== |
Diesmal trifft die weiße Kugel nicht mittig auf die ruhende schwarze Acht. | Diesmal trifft die weiße Kugel nicht mittig auf die ruhende schwarze Acht. | ||
| + | [[Datei:Aufgaben_Impuls_Billiard_II.jpg|thumb|none|866px]] | ||
*Konstruiere mit einer Zeichnung welchen Impuls die weiße Kugel nach dem Zusammenstoß hat. | *Konstruiere mit einer Zeichnung welchen Impuls die weiße Kugel nach dem Zusammenstoß hat. | ||
| + | |||
| + | |||
| + | ===[[Aufgaben zur Impulserhaltung - Lösungen|Lösungen]]=== | ||
Aktuelle Version vom 26. Mai 2017, 10:54 Uhr
(Klassische Mechanik > Impulserhaltung)
Inhaltsverzeichnis
Ein Ruderboot
Beschreibe mit Hilfe des Impulses, wie das Ruderboot losfährt und warum es ohne zu Rudern wieder langsamer wird.
Raumstation Mir
Im Europapark ist ein Trainingsmodul der ehemaligen russischen Raumstation Mir zu besichtigen. Dabei fallen unter anderem kleine Düsen ins Auge, die zur Lagekorrektur gedacht sind.
- Wie kann man mit den Steuerdüsen die Mir drehen oder verschieben?
- Mache dazu eine Zeichnung und zeichne auch die Lage und Richtung der Düsen ein.
- Wieviele Steuerdüsen braucht man, um die Raumstation in alle beliebigen Richtung zu drehen oder zu verschieben?
- Zusätzlich hatte die Mir noch Kreisel zur Stabilisierung und Steuerung.
Astronaut in der ISS
Astronauten in der ISS bewegen sich fort, indem sie sich an den Wänden der Raumstation abdrücken. Alexander Gerst drückt sich mit einem kräftigen Schubs von der Bordwand ab und erreicht so eine Geschwindigkeit von 1 m/s.
- Mit welcher Geschwindigkeit bewegt sich durch das Abdrücken nun die ISS? Schätze notwendige Daten ab oder recherchiere im Netz.
Die Welt bewegen
Können Menschen die ganze Erde in Bewegung versetzen? Vielleicht, wenn sämtliche Einwohner Chinas mitmachen! Sie springen gleichzeitig zusammen nach oben. Dabei springen sie mit ca. 2,5m/s ab. (Damit erreichen sie eine Höhe von 30cm.)
- Welche Bewegung führt die Erde während des Sprungs aus?
Ein Mensch hat eine Masse von ca. 50kg, es gibt ca. 7 Millierden Einwohner in China und die Erde hat eine Masse von ca. [math]6 \cdot 10^{24}\,\rm kg[/math].
- Wie schnell wird die Erde durch den Sprung? Berechne die Geschwindigkeit in m/s und in Meter pro Jahr!
Elfmeter
Bei einem Elfmeter hält der Torwart den Ball während er springt, also keinen Kontakt zum Boden hat.
- Warum wird er dadurch ein wenig in Richtung des Tors beschleunigt?
- Welche Angaben benötigt man, um die Impulsmenge des Balles zu bestimmen? Bestimme die Impulsmenge mit den geschätzten Werten.
Auch bei den folgenden Fragen fehlen Angaben, um die Lösung zu bestimmen. Überlege dir zuerst welche Angaben fehlen, schätze dann sinnvolle Werte oder recherchiere.
- Mit welcher Geschwindigkeit bewegt sich nach dem Festhalten der Torwart auf die Torlinie zu?
- Wie stark sind beim Fangen die Kräfte auf den Ball und den Torwart ?
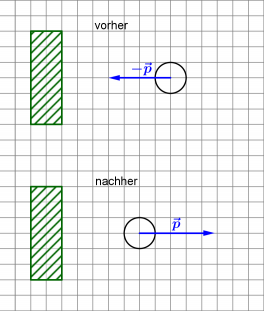
Billard I
Beim Billiardspielen wird eine Kugel senkrecht zur Bande gespielt. Von Reibungsverlusten abgesehen prallt sie mit genau dem entgegengesetzten Impuls wieder zurück.
Stellt man nun eine Impulsbilanz auf, so stellt man fest, dass die Summe der Impulse nicht gleich geblieben ist. Es fehlt die Impulsmenge [math]2\vec p[/math]!
- Wo ist der fehlende Impuls?
Ein Segelboot
Ein Segelboot hat den Spinnaker gesetzt. Dadurch wird der Rückenwind gebremst.
- Beschreibe, wie sich dadurch der Impuls der Luft und des Bootes ändert.
- Um die Geschwindigkeit des Bootes 10 Sekunden nach dem Start abzuschätzen, benötigt man die Masse des Bootes mit 2000kg und die Segelfläche von 50 m^2. Außerdem muss man wissen, dass ein Liter Luft eine Masse von ca. 1 Gramm hat. Der Wind pustet mit 5 m/sec und wird auf 1 m/sec abgebremst.
- Rechenweg: >Luftvolumen >Luftmasse >Luftimpuls >Änderung des Luftimpulses >Bootimpuls >Bootgeschwindigkeit.
- Warum ist die real erreichte Geschwindigkeit des Bootes bestimmt geringer?
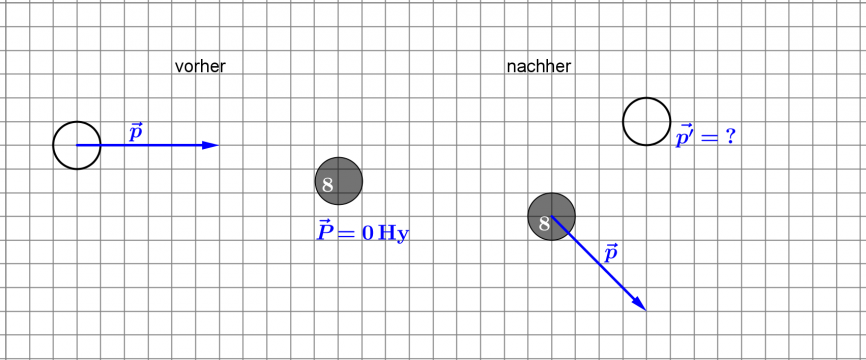
Billard II
Diesmal trifft die weiße Kugel nicht mittig auf die ruhende schwarze Acht.
- Konstruiere mit einer Zeichnung welchen Impuls die weiße Kugel nach dem Zusammenstoß hat.