*: Unterschied zwischen den Versionen
| Zeile 1: | Zeile 1: | ||
| − | __NOTOC__ | + | __NOTOC__==Spule und Magnetfeld als Energiespeicher== |
| − | == | + | ====Selbstinduktion==== |
| − | + | :'''a)''' Erklären Sie den Begriff der Selbstinduktion indem Sie einen passenden Versuch beschreiben. | |
| − | + | :'''b)''' Begründen Sie, warum die Spannung der Selbstinduktion an einer Spule proportional zur Änderung der Stromstärke ist. | |
| − | + | ====Induktivität und Energiegehalt einer Spule==== | |
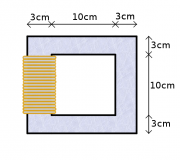
| + | [[Datei:Aufgabe_Spule_mit_Eisenkern.png|thumb]] | ||
| + | :'''a)''' Eine Spule hat eine Induktivität von 10 H (Henry). | ||
| + | :Was bedeutet das? Erläutern Sie es anhand von Verwendungsbeispielen. | ||
| + | :'''b)''' Eine Spule hat 1000 Windungen, eine Querschnittsfläche von 3cm x 3cm und eine Länge von 10cm. | ||
| + | :a) Berechnen Sie ihre Induktivität. | ||
| + | Man läßt einen Strom mit der Stärke von 2A durch die Spule fließen. | ||
| + | :b) Berechnen Sie den magnetischen Fluss, die Feldstärke, die Energiemenge und die Energiedichte der Spule. | ||
| + | Die stromdurchflossene Spule wird nun in einen geschlossenen Eisenkern mit der relativen Permeabilität von 2000 gestellt. | ||
| + | :c) Wie verändern sich dadurch die Werte von Frage b)? | ||
| − | + | ====Energie des Erdmagnetfeldes==== | |
| + | Das Erdmagnetfeld hat in Europa eine Feldstärke von ca. 40A/m, bzw. eine Flußdichte von ca.50 MikroTesla. | ||
| − | + | :Wieviel Energie ist innerhalb Ihres Zimmers im Erdmagnetfeld gespeichert? | |
| − | + | :Wie hoch könnte man damit eine Tafel Schokolade heben? | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
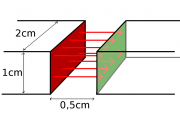
| − | + | [[Datei:Aufgabe_Feld_zwischen_Stabmagnet.png|thumb]] | |
| + | ====Feldenergie von Festmagneten==== | ||
| + | Zwei Festmagnete "haften" aneinander und werden bis auf einen Abstand von 0,5cm auseinandergezogen. Wieviel Energie war wohl dazu nötig? | ||
| + | |||
| + | Näherungsweise nimmt man das Feld zwischen den Polen als homogen an. | ||
| + | Die Feldstärke zwischen den Polen wird zu 120000A/m gemessen. (Die Flußdichte beträgt 0,15T.) | ||
| − | + | ===supraleitender Energiespeicher=== | |
| − | + | Supraleiter sind Materialien, die bei niedrigen Temperaturen keinen ohmschen Widerstand mehr haben. Daraus kann man supraleitende Kabel herstellen und auch Spulen wickeln. | |
| + | :a) Entwerfen Sie eine supraleitende Spule, welche die Energie eines Liters Benzin (ca. 40MJ) speichern kann. | ||
| + | :b) Welche Vor- und Nachteile hätte die Verwendung eines Eisenkerns? | ||
| − | + | ===Bewegungsenergie der Elektronen=== | |
| − | + | Bei einer stromdurchflossenen Spule bewegen sich die Ladungsträger, in diesem Fall also die Elektronen. In dieser Bewegung steckt auch Energie. Vielleicht ist dort auch die Energie der Spule gespeichert und nicht im Magnetfeld? Als Beispiel nehmen wir eine Spule mit 1000 Windungen, einer Querschnittsfläche von 3cm x 3cm und einer Länge von 10cm. | |
| − | + | <br>Zunächst muss man die Masse der im Kupferdraht frei beweglichen Elektronen berechnen. Der Draht hat eine Masse von 120g. Jedes Kupferatom stellt ungefähr ein Leitungselektron zur Verfügung. Die Dichte von Kupfer beträgt ca. 9 g/cm^3 und das molare Volumen beträgt ca. 7*10^-6 m^3/mol. | |
| − | + | :a) Wieviel Masse haben die Leitungselektronen des Kupferdrahtes? | |
| − | + | :b) Welche Geschwindigkeit müßten die Elektronen haben, um die Energie bei einer Stromstärke von 2A zu speichern? | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
Version vom 10. Oktober 2017, 09:46 Uhr
Spule und Magnetfeld als Energiespeicher
Selbstinduktion
- a) Erklären Sie den Begriff der Selbstinduktion indem Sie einen passenden Versuch beschreiben.
- b) Begründen Sie, warum die Spannung der Selbstinduktion an einer Spule proportional zur Änderung der Stromstärke ist.
Induktivität und Energiegehalt einer Spule
- a) Eine Spule hat eine Induktivität von 10 H (Henry).
- Was bedeutet das? Erläutern Sie es anhand von Verwendungsbeispielen.
- b) Eine Spule hat 1000 Windungen, eine Querschnittsfläche von 3cm x 3cm und eine Länge von 10cm.
- a) Berechnen Sie ihre Induktivität.
Man läßt einen Strom mit der Stärke von 2A durch die Spule fließen.
- b) Berechnen Sie den magnetischen Fluss, die Feldstärke, die Energiemenge und die Energiedichte der Spule.
Die stromdurchflossene Spule wird nun in einen geschlossenen Eisenkern mit der relativen Permeabilität von 2000 gestellt.
- c) Wie verändern sich dadurch die Werte von Frage b)?
Energie des Erdmagnetfeldes
Das Erdmagnetfeld hat in Europa eine Feldstärke von ca. 40A/m, bzw. eine Flußdichte von ca.50 MikroTesla.
- Wieviel Energie ist innerhalb Ihres Zimmers im Erdmagnetfeld gespeichert?
- Wie hoch könnte man damit eine Tafel Schokolade heben?
Feldenergie von Festmagneten
Zwei Festmagnete "haften" aneinander und werden bis auf einen Abstand von 0,5cm auseinandergezogen. Wieviel Energie war wohl dazu nötig?
Näherungsweise nimmt man das Feld zwischen den Polen als homogen an. Die Feldstärke zwischen den Polen wird zu 120000A/m gemessen. (Die Flußdichte beträgt 0,15T.)
supraleitender Energiespeicher
Supraleiter sind Materialien, die bei niedrigen Temperaturen keinen ohmschen Widerstand mehr haben. Daraus kann man supraleitende Kabel herstellen und auch Spulen wickeln.
- a) Entwerfen Sie eine supraleitende Spule, welche die Energie eines Liters Benzin (ca. 40MJ) speichern kann.
- b) Welche Vor- und Nachteile hätte die Verwendung eines Eisenkerns?
Bewegungsenergie der Elektronen
Bei einer stromdurchflossenen Spule bewegen sich die Ladungsträger, in diesem Fall also die Elektronen. In dieser Bewegung steckt auch Energie. Vielleicht ist dort auch die Energie der Spule gespeichert und nicht im Magnetfeld? Als Beispiel nehmen wir eine Spule mit 1000 Windungen, einer Querschnittsfläche von 3cm x 3cm und einer Länge von 10cm.
Zunächst muss man die Masse der im Kupferdraht frei beweglichen Elektronen berechnen. Der Draht hat eine Masse von 120g. Jedes Kupferatom stellt ungefähr ein Leitungselektron zur Verfügung. Die Dichte von Kupfer beträgt ca. 9 g/cm^3 und das molare Volumen beträgt ca. 7*10^-6 m^3/mol.
- a) Wieviel Masse haben die Leitungselektronen des Kupferdrahtes?
- b) Welche Geschwindigkeit müßten die Elektronen haben, um die Energie bei einer Stromstärke von 2A zu speichern?