*: Unterschied zwischen den Versionen

Version vom 17. Oktober 2017, 21:21 Uhr (Quelltext anzeigen) Patrick.Nordmann (Diskussion | Beiträge) ← Zum vorherigen Versionsunterschied		Version vom 17. Oktober 2017, 21:26 Uhr (Quelltext anzeigen) Patrick.Nordmann (Diskussion | Beiträge) Zum nächsten Versionsunterschied →
Zeile 1:		Zeile 1:
	__NOTOC__		__NOTOC__
−		+	==Aufgaben zu Schwingungen I==
	====Energieformen====		====Energieformen====
	Nennen Sie zwei verschiedene Beispiele für eine Schwingung und beschreiben Sie kurz wann dabei welche Energieformen auftreten.		Nennen Sie zwei verschiedene Beispiele für eine Schwingung und beschreiben Sie kurz wann dabei welche Energieformen auftreten.
Zeile 80:		Zeile 80:
	*Berechnen Sie die maximale Geschwindigkeit <math>\hat v</math> und die maximale Beschleunigung <math>\hat a</math> aus der Winkelgeschwindigkeit <math>\omega</math>.		*Berechnen Sie die maximale Geschwindigkeit <math>\hat v</math> und die maximale Beschleunigung <math>\hat a</math> aus der Winkelgeschwindigkeit <math>\omega</math>.
	:Kontrollieren Sie ihr Ergebnis an den Graphen von <math>v(t)</math> und <math>a(t)</math>.		:Kontrollieren Sie ihr Ergebnis an den Graphen von <math>v(t)</math> und <math>a(t)</math>.
		+
		+	==Fußnoten==
		+	<references />

---

Version vom 17. Oktober 2017, 21:26 Uhr

Aufgaben zu Schwingungen I

Energieformen

Nennen Sie zwei verschiedene Beispiele für eine Schwingung und beschreiben Sie kurz wann dabei welche Energieformen auftreten.

Schaukeltier

Ein Kind "reitet" auf einem Feder-Schaukeltier. Erklären Sie anhand dieses Beispiels die Begriffe:

• Ruhelage
• Elongation
• Amplitude
• Rückstellkraft
• Periodendauer
• Frequenz

Nennen Sie noch ein weiteres Beispiel für eine mechanische Schwingung und machen Sie sich wiederum diese Begriffe klar.

Zeigermodell

Wie kann man eine harmonische Schwingung mit einem Zeiger beschreiben?

Beschreiben Sie dazu den im Unterricht durchgeführten Versuch.

Uhrzeiger

Eine Uhr hat einen Stunden-, einen Minuten- und einen Sekundenzeiger.

• Begründen Sie warum der Sekundenzeiger eine Winkelgeschwindigkeit von $$\omega = \frac{2\, \pi}{60\, \rm s}$$ hat.
• Welche Frequenz und welche Periodendauer hat der Sekundenzeiger?
• Mit welcher Geschwindigkeit $$v$$ bewegt sich die Spitze des Sekundenzeigers, wenn er 10cm lang ist?
• Suchen Sie eine Armbanduhr oder eine Wanduhr und bestimmen Sie für alle drei Zeiger die Größen: $$\omega$$ , $$f$$ , $$T$$ und $$v$$ .

Schwingmännchen

Ein Schwingmännchen schwingt mit einer Periodendauer von

$$\rm T = 0{,}5\, s$$ und einer Amplitude von $$\hat y = \rm 3\, cm$$ .

Die Zeit

$$t$$ wird ab dem Durchgang von unten nach oben durch die Ruhelage gemessen.

• Zeichnen Sie für folgende Zeitpunkte den Zeiger in ein Koordinatensystem: $$t_1 = 0{,}25\, s$$ , $$t_2 = 0{,}125\, s$$ , $$t_3 = 0{,}4375\, s$$

• Bestimmen Sie zeichnerisch jeweils die Auslenkungen $$y(t_i)$$ .

Stimmgabel

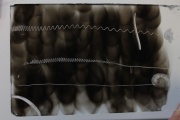
Die Zinken einer Stimmgabel schwingen mit einer Frequenz von 440 Hz^[1] und durch eine Messung an einer verußten Glasplatte bestimmt man die größte Amplitude zu

$$\hat y = 2 \, \rm mm$$ .

• Welche Periodendauer und welche Winkelgeschwindigkeit hat die Schwingung?
• Stellen Sie für einen Zinken der Stimmgabel die Bewegungsgleichungen auf:

$$y(t)$$ , $$v(t)$$ , $$a(t)$$ ,

• Bestimmen Sie daraus die maximale Geschwindigkeit und die maximale Beschleunigug eines Zinkens der Stimmgabel.

Horizontales Federpendel

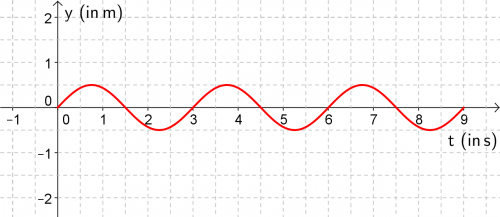
Ein Wagen schwingt horizontal an einer Feder. Die folgenden Graphen beschreiben den Verlauf seiner Bewegung im Koordinatensystem:

• Woran kann man erkennen, dass die Schwingung nicht gedämpft ist, also keine Energie verliert?

• Wie wurde dem Wagen zu Beginn Energie zugeführt? Wurde er ausgelenkt und losgelassen? (und wenn ja, in welche Richtung?) Wurde er angeschubst? (und wenn ja, in welche Richtung?)

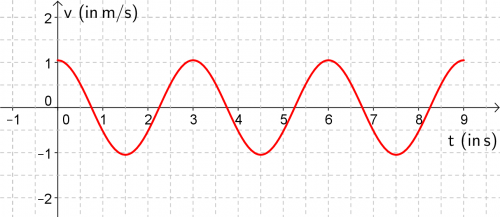
Der Graph der Geschwindigkeit ist gegenüber dem der Auslenkung um eine Viertel Periode (

$$\frac{T}{4}$$ oder $$\frac{2\, \pi}{4}$$ ) verschoben.

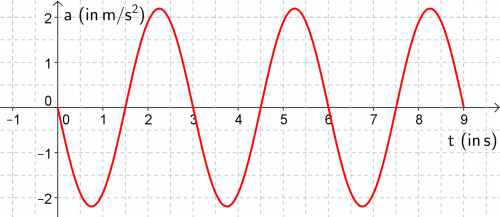
Der Graph der Beschleunigung ist gegenüber dem der Auslenkung um eine Halbe Periode (

$$\frac{T}{2}$$ oder $$\frac{2\, \pi}{2}$$ ) verschoben und hat immer ein anderes Vorzeichen als die Auslenkung.

• Erklären Sie das anhand der Bewegung des Wagens. (Nicht mathematisch über die Ableitung.)

• Berechnen Sie die maximale Geschwindigkeit $$\hat v$$ und die maximale Beschleunigung $$\hat a$$ aus der Winkelgeschwindigkeit $$\omega$$ .

Kontrollieren Sie ihr Ergebnis an den Graphen von $$v(t)$$ und $$a(t)$$ .

Fußnoten

1. Hochspringen ↑ Das ist der Kammerton a. (Siehe auch Wikipedia: Kammerton)