Aufgaben zum Film "Wegweisende Echos" (Lösungen): Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „'''1)''' Drei Kilometer entfernt gibt es einen Blitz. <br/>Zeichne ein Koordinatensystem mit der x-Achse als Zeitachse (von 0 sec bis 10 sec) und der y-Achse…“) |
|||
| Zeile 7: | Zeile 7: | ||
'''2)''' Das Echolot arbeitet mit Schallwellen im Wasser, die eine Geschwindigkeit von <math>\underline{\quad \rm 1500 \quad} \rm \frac{m}{sec}</math> haben. | '''2)''' Das Echolot arbeitet mit Schallwellen im Wasser, die eine Geschwindigkeit von <math>\underline{\quad \rm 1500 \quad} \rm \frac{m}{sec}</math> haben. | ||
<br/>Das Wasser hat eine Tiefe von 73,5m (21,6m 9,7m 2,4m). Wie lange braucht der Schall vom Echolot zum Boden und zurück? | <br/>Das Wasser hat eine Tiefe von 73,5m (21,6m 9,7m 2,4m). Wie lange braucht der Schall vom Echolot zum Boden und zurück? | ||
| + | :Im Wasser legt der Schall in einer Sekunde eine Strecke von 1500 Metern zurück. | ||
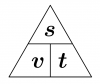
| + | :Bei dem Echolot legt der Schall erst den Hinweg, dann den Rückweg zurück, insgesamt also die doppelte Wassertiefe![[Datei:Dreisatz_svt.png|thumb|100px|Merkregel]] | ||
| + | :Jetzt kann man die Laufzeit berechnen: | ||
| + | :mit einer Formel: <math>t=\frac{s}{v} =\frac{147\,\rm m}{1500\,\rm\frac{m}{sec}} = 0{,}098\,\rm sec \approx 0{,}1\,\rm sec</math> | ||
| + | :oder als Dreisatz: | ||
| + | Zeit | Strecke | ||
| + | 1sec | 1500m :1500 | ||
| + | 1/1500sec | 1m *147 | ||
| + | 0,098sec | 147m | ||
| + | :{| | ||
| + | | | ||
| + | Für die anderen Wassertiefen erhält man noch kürzere Zeiten: | ||
| + | | | ||
| + | {| class="wikitable" | ||
| + | |Wassertiefe|| 21,6m || 9,7m || 2,4m | ||
| + | |- | ||
| + | |Laufzeit || 0,0288sec || 0,01293sec ||0,0032sec | ||
| + | |} | ||
| + | |} | ||
'''3)''' Ein Echolot misst eine Laufzeit des Schalls von 0,067sec. Wie tief ist das Wasser? | '''3)''' Ein Echolot misst eine Laufzeit des Schalls von 0,067sec. Wie tief ist das Wasser? | ||
| + | :Diesmal will man die Entfernung, also die Strecke <math>s</math>, wissen: | ||
| + | :mit einer Formel: <math>s=v\cdot t = 1500\rm\frac{m}{sec}\cdot 0{,}067\,\rm sec = 100{,}5\,\rm m</math> | ||
| + | :oder als Dreisatz: [[Datei:Dreisatz_svt.png|thumb|100px|Merkregel]] | ||
| + | Zeit | Strecke | ||
| + | 1sec | 1500m *0,067 | ||
| + | 0,067sec | 100,5m | ||
| + | :Das Wasser ist aber nur 50,25m tief, denn der Schall muss ja den Hinweg und den Rückweg zurücklegen! | ||
'''4)''' Wozu und wie benutzen Delfine Schall unter Wasser? | '''4)''' Wozu und wie benutzen Delfine Schall unter Wasser? | ||
| + | :Delfine senden Klicklaute aus und hören deren Echo. Sie hören wieviel Zeit vergeht, bis das Echo wiederkommt und aus welcher Richtung das Echo kommt. Damit können sie bei der Jagd Beutefische orten. | ||
'''5)''' Erkläre, wie ein Sonar funktioniert. Wozu kann man es einsetzen? | '''5)''' Erkläre, wie ein Sonar funktioniert. Wozu kann man es einsetzen? | ||
| + | :Ein Sonar funktioniert wie die Schallortung der Delfine. Von einem Boot aus werden kurze Schallimpulse in alle Richtungen ausgesendet. Dann misst man aus welcher Richtung das Echo kommt und wie lange der Schall unterwegs war. Daraus kann man berechnen in welcher Richtung und in welcher Entfernung der Schall reflektiert wurde. | ||
| + | :Beim Fischfang kann man damit Fischschwärme orten. Das Militär benutzt es zum Auffinden von U-Booten. | ||
'''6)''' Sonare können auch gefährlich sein! Erläutere, was damit gemeint ist. | '''6)''' Sonare können auch gefährlich sein! Erläutere, was damit gemeint ist. | ||
| + | :Die lauten Signale der Sonare können die im Wasser lebenden Tiere gefährden. So verlieren Wale durch starke Sonare ihren Orientierungssinn und können stranden. | ||
'''7)''' Auch Radar arbeit mit einem Echo, aber es werden keine Schallwellen, sondern <math>\underline{\qquad \text{elektro-magnetische} \qquad }</math>Wellen eingesetzt. Sie breiten sich mit der Geschwindigkeit von Licht aus, also mit <math>\underline{\qquad \text{300.000} \qquad } \rm \frac{km}{sec}</math>. | '''7)''' Auch Radar arbeit mit einem Echo, aber es werden keine Schallwellen, sondern <math>\underline{\qquad \text{elektro-magnetische} \qquad }</math>Wellen eingesetzt. Sie breiten sich mit der Geschwindigkeit von Licht aus, also mit <math>\underline{\qquad \text{300.000} \qquad } \rm \frac{km}{sec}</math>. | ||
'''8)''' Wie erreicht man, dass Radar in alle Richtungen „schauen“ kann? | '''8)''' Wie erreicht man, dass Radar in alle Richtungen „schauen“ kann? | ||
| + | :Die Antenne, welche die Wellen aussendet, dreht sich. Dadurch werden in alle Richtungen Signale ausgesendet und deren Echo wieder empfangen. | ||
'''9)''' Wozu setzt man Radar ein? Nenne möglichst viele Anwendungen. | '''9)''' Wozu setzt man Radar ein? Nenne möglichst viele Anwendungen. | ||
| + | :Schiffe und Flugzeuge haben ein Radar an Bord um Schiffe, Flugzeuge und andere Hindernisse auch bei schlechtem Wetter zu "sehen". | ||
| + | :An Flughäfen überwachen Fluglotsen den Flugverkehr, damit die Flugzeuge nicht zusammenstoßen. | ||
| + | :Mit [http://www.wettergefahren.de/wetter/deutschland/aktuell/radarfilm.html Radarstationen des Deutschen Wetterdienstes] können Regenwolken, Hagel und Gewitter geortet werden. Das hilft, um im Alltag nicht nass zu werden, aber auch beim Schutz gegen Unwetter. | ||
| + | :Das SpaceShuttle hat mit einer Radar-Sendeantenne und zwei Empfangsantennen die Oberfläche der Erde dreidimensional vermessen. | ||
'''10)''' Ein Flugzeug ist 100km entfernt. Wie lange brauchen die Radarwellen zum Flugzeug und zurück? | '''10)''' Ein Flugzeug ist 100km entfernt. Wie lange brauchen die Radarwellen zum Flugzeug und zurück? | ||
| + | :Das Radar arbeitet mit elektromagnetischen Wellen, die sich viel schneller als der Schall ausbreiten, nämlich mit <math>300.000\, \rm \frac{km}{sec}</math>. | ||
| + | :Die Berechnung der Zeit geht aber genauso wie mit einer Schallwelle: | ||
| + | :mit einer Formel: <math>t=\frac{s}{v} =\frac{100\,\rm km}{300.000\,\rm\frac{km}{sec}} \approx 0{,}00033\,\rm sec</math> | ||
| + | :oder als Dreisatz: | ||
| + | Zeit | Strecke | ||
| + | 1sec | 300.000km :3 | ||
| + | 0,33sec | 100.000km :1000 | ||
| + | 0,00033sec | 100km | ||
Version vom 28. November 2017, 19:11 Uhr
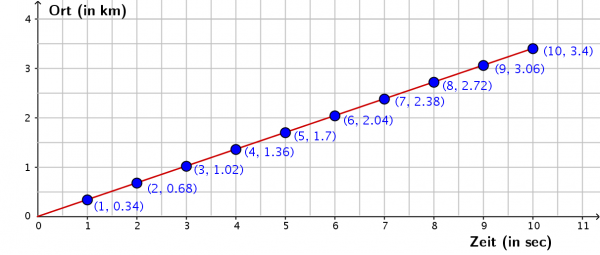
1) Drei Kilometer entfernt gibt es einen Blitz.
Zeichne ein Koordinatensystem mit der x-Achse als Zeitachse (von 0 sec bis 10 sec) und der y-Achse als Ortsachse (von 0km bis 4km).
Zeichne mit einem Graphen ein, wie sich der Donner mit 340 m/sec ausbreitet.
- Der Schall breitet sich in jeder Sekunde um 340m aus:
2) Das Echolot arbeitet mit Schallwellen im Wasser, die eine Geschwindigkeit von [math]\underline{\quad \rm 1500 \quad} \rm \frac{m}{sec}[/math] haben.
Das Wasser hat eine Tiefe von 73,5m (21,6m 9,7m 2,4m). Wie lange braucht der Schall vom Echolot zum Boden und zurück?
- Im Wasser legt der Schall in einer Sekunde eine Strecke von 1500 Metern zurück.
- Bei dem Echolot legt der Schall erst den Hinweg, dann den Rückweg zurück, insgesamt also die doppelte Wassertiefe!
- Jetzt kann man die Laufzeit berechnen:
- mit einer Formel: [math]t=\frac{s}{v} =\frac{147\,\rm m}{1500\,\rm\frac{m}{sec}} = 0{,}098\,\rm sec \approx 0{,}1\,\rm sec[/math]
- oder als Dreisatz:
Zeit | Strecke
1sec | 1500m :1500
1/1500sec | 1m *147
0,098sec | 147m
Für die anderen Wassertiefen erhält man noch kürzere Zeiten:
Wassertiefe 21,6m 9,7m 2,4m Laufzeit 0,0288sec 0,01293sec 0,0032sec 3) Ein Echolot misst eine Laufzeit des Schalls von 0,067sec. Wie tief ist das Wasser?
- Diesmal will man die Entfernung, also die Strecke [math]s[/math], wissen:
- mit einer Formel: [math]s=v\cdot t = 1500\rm\frac{m}{sec}\cdot 0{,}067\,\rm sec = 100{,}5\,\rm m[/math]
- oder als Dreisatz:
Zeit | Strecke 1sec | 1500m *0,067 0,067sec | 100,5m
- Das Wasser ist aber nur 50,25m tief, denn der Schall muss ja den Hinweg und den Rückweg zurücklegen!
4) Wozu und wie benutzen Delfine Schall unter Wasser?
- Delfine senden Klicklaute aus und hören deren Echo. Sie hören wieviel Zeit vergeht, bis das Echo wiederkommt und aus welcher Richtung das Echo kommt. Damit können sie bei der Jagd Beutefische orten.
5) Erkläre, wie ein Sonar funktioniert. Wozu kann man es einsetzen?
- Ein Sonar funktioniert wie die Schallortung der Delfine. Von einem Boot aus werden kurze Schallimpulse in alle Richtungen ausgesendet. Dann misst man aus welcher Richtung das Echo kommt und wie lange der Schall unterwegs war. Daraus kann man berechnen in welcher Richtung und in welcher Entfernung der Schall reflektiert wurde.
- Beim Fischfang kann man damit Fischschwärme orten. Das Militär benutzt es zum Auffinden von U-Booten.
6) Sonare können auch gefährlich sein! Erläutere, was damit gemeint ist.
- Die lauten Signale der Sonare können die im Wasser lebenden Tiere gefährden. So verlieren Wale durch starke Sonare ihren Orientierungssinn und können stranden.
7) Auch Radar arbeit mit einem Echo, aber es werden keine Schallwellen, sondern [math]\underline{\qquad \text{elektro-magnetische} \qquad }[/math]Wellen eingesetzt. Sie breiten sich mit der Geschwindigkeit von Licht aus, also mit [math]\underline{\qquad \text{300.000} \qquad } \rm \frac{km}{sec}[/math].
8) Wie erreicht man, dass Radar in alle Richtungen „schauen“ kann?
- Die Antenne, welche die Wellen aussendet, dreht sich. Dadurch werden in alle Richtungen Signale ausgesendet und deren Echo wieder empfangen.
9) Wozu setzt man Radar ein? Nenne möglichst viele Anwendungen.
- Schiffe und Flugzeuge haben ein Radar an Bord um Schiffe, Flugzeuge und andere Hindernisse auch bei schlechtem Wetter zu "sehen".
- An Flughäfen überwachen Fluglotsen den Flugverkehr, damit die Flugzeuge nicht zusammenstoßen.
- Mit Radarstationen des Deutschen Wetterdienstes können Regenwolken, Hagel und Gewitter geortet werden. Das hilft, um im Alltag nicht nass zu werden, aber auch beim Schutz gegen Unwetter.
- Das SpaceShuttle hat mit einer Radar-Sendeantenne und zwei Empfangsantennen die Oberfläche der Erde dreidimensional vermessen.
10) Ein Flugzeug ist 100km entfernt. Wie lange brauchen die Radarwellen zum Flugzeug und zurück?
- Das Radar arbeitet mit elektromagnetischen Wellen, die sich viel schneller als der Schall ausbreiten, nämlich mit [math]300.000\, \rm \frac{km}{sec}[/math].
- Die Berechnung der Zeit geht aber genauso wie mit einer Schallwelle:
- mit einer Formel: [math]t=\frac{s}{v} =\frac{100\,\rm km}{300.000\,\rm\frac{km}{sec}} \approx 0{,}00033\,\rm sec[/math]
- oder als Dreisatz:
Zeit | Strecke 1sec | 300.000km :3 0,33sec | 100.000km :1000 0,00033sec | 100km