|
|
| (29 dazwischenliegende Versionen des gleichen Benutzers werden nicht angezeigt) |
| Zeile 1: |
Zeile 1: |
| | + | ([[Inhalt_Klasse_10|'''Klassische Mechanik''']] > [[Inhalt_Klasse_10#Trägheit_und_Impuls|'''Trägheit und Impuls''']]) |
| | + | |
| | ==Beispiele== | | ==Beispiele== |
| | <gallery widths=150px heights=130px perrow=4 > | | <gallery widths=150px heights=130px perrow=4 > |
| − | Bild:Curling_Abstoß.jpg|Beim Curling muss man dem Stein den richtigen Schwung mitgeben, | + | Bild:Luftgewehr Kugel.jpg|Eine Luftgewehrkugel |
| − | Bild:Curling_Besen.jpg|damit er genau am Ziel stehenbleibt. | + | Bild:Holzbrett Luftgewehr.jpg|kann dieses Brettchen umstoßen! |
| − | Bild:Shopping_cart_New_York.jpg|Schon mal mit einem leeren Einkaufswagen | + | Bild:Golfball.jpg|Diese Bälle... |
| − | Bild:Einkaufswagen_voll.png|oder mit einem vollen Einkaufswagen durch einen Laden gefahren? | + | Bild:Tennisball.jpg|...können das auch. |
| | + | Bild:Curling_Abstoß.jpg|<ref>[http://commons.wikimedia.org/wiki/File:Martin_Sesaker_at_the_2012_Youth_Winter_Olympics.jpg Bild von Ralf Roletschek, CC by SA 3.0]</ref>Beim Curling muss man dem Stein den richtigen Schwung mitgeben, |
| | + | Bild:Curling_Besen.jpg|damit er genau am Ziel stehenbleibt. |
| | + | Bild:Luftkissenpuck.jpg|Wie funktioniert dieser "Fußball"? |
| | + | Bild:Einkaufswagen_voll.png| Wie bewegt sich ein "angeschubster" Einkaufswagen? |
| | </gallery> | | </gallery> |
| | | | |
| − | * Beispiel mit reibungsarmen Einkaufswagen: Der Wagen bewegt sich geradlinig und behält seine Geschwindigkeit bei. Auch die Drehung des Wagen ändert sich nicht. | + | *Verschiedene Bälle, am besten gleich groß aber mit unterschiedlichen Massen, fangen und werfen. (Oder "Kegeln", denn dabei spielt die Gewichtskraft keine Rolle. Oder "Dosenwerfen" mit verschiedenen Bällen.) |
| | *Ein sich schnell drehendes Fahrrad-Rad kann man nicht so ohne weiteres anschubsen, abbremsen oder kippen. Es "wehrt sich". | | *Ein sich schnell drehendes Fahrrad-Rad kann man nicht so ohne weiteres anschubsen, abbremsen oder kippen. Es "wehrt sich". |
| − | *Verschiedene Bälle, am besten gleich groß aber mit unterschiedlichen Massen, fangen und werfen. | + | * Beispiel mit reibungsarmen Einkaufswagen: Der Wagen bewegt sich geradlinig und behält seine Geschwindigkeit bei. Auch die Drehung des Wagen ändert sich nicht. |
| | | | |
| − | Weitere Beispiele sind der Luftkissenpuck (Fußball), ein Mensch auf einem Bürodrehstuhl oder Experimente am Luftkissentisch oder -bahn. | + | Weitere Beispiele sind der Luftkissenpuck (Fußball), ein Mensch auf einem Bürodrehstuhl oder Experimente am Luftkissentisch oder -bahn. |
| | | | |
| − | ==(Dreh-)Impuls als Bewegungsmenge== | + | ==(Dreh-)Impuls als Bewegungsmenge== |
| | + | ====Definition des (Dreh-) Impulses==== |
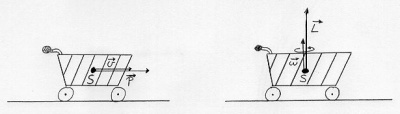
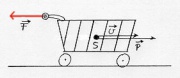
| | [[Image:Mechanik_Bewegungszustand.jpg|thumb|400px|Die Bewegungsmenge eines Einkaufswagens.]] | | [[Image:Mechanik_Bewegungszustand.jpg|thumb|400px|Die Bewegungsmenge eines Einkaufswagens.]] |
| − | *Die Bewegung eines Körpers kann man als eine Überlagerung einer Translation im Raum und eine Drehung in sich beschreiben. | + | * Ein Ball enthält viel "Bewegung", wenn er eine große Masse hat und er schnell ist. Die physikalische Größe, welche die Bewegungsmenge angibt, heißt "Impuls". Man legt den Impuls daher als Produkt von Masse und Geschwindigkeit fest. |
| − | | + | :Leider hat die Einheit des Impulses keinen allgemeingültigen eigenen Namen bekommen, im Karlsruher Physikkurs wird sie nach [https://de.wikipedia.org/wiki/Christiaan_Huygens Christiaan Huygens] (1629–1695) benannt. |
| − | *Die Bewegung wird durch die Menge an Impuls <math>\vec p</math>(Schwung) für die Translation und Drehimpuls <math>\vec L</math> (Drehschwung) für die Rotation angegeben.
| + | *Umgangssprachlich versteht man unter "Impuls" etwas anderes als in der Physik! |
| − | | + | **Eine Anregung, ein Anreiz, ein Ansporn: "Der Telefonanruf ihrer Freundin war der entscheidende Impuls doch noch für die Arbeit zu lernen." ; "Der Comic ist ein guter Impuls für eine Diskussion." |
| − | *Sowohl Impuls als auch Drehimpuls haben eine Richtung und sind vektorielle Größen. Sie geben an, wieviel Schwung, bzw. Drehschwung ein Gegenstand hat, also wieviel "Bewegungsmenge" in dem Körper steckt. Ausserdem gibt er an in welche Richtung er sich bewegt, bzw. um welche Achse er sich dreht.
| + | **Etwas plötzliches, kurzzeitiges: "Manchmal handelt er sehr impulsiv ohne nachzudenken." |
| − | | + | |
| − | *In der Schulphysik betrachtet man in der Regel Bewegungen von Gegenständen, bei denen die Drehbewegung keine Rolle spielt und beschreibt nur die Translation.
| + | |
| − | | + | |
| − | ===Definition des (Dreh-)Impulses===
| + | |
| − | * Ein Ball enthält viel Impuls, wenn er schnell ist und er eine große Masse hat. Man legt den Impuls daher als Produkt der beiden Größen fest.
| + | |
| − | :Leider hat die Einheit des Impulses keinen allgemeingültigen eigenen Namen bekommen, im Karlsruher Physikkurs wird sie nach Christiaan Huygens (1629–1695) benannt. | + | |
| − | | + | |
| | :{|class="wikitable" | | :{|class="wikitable" |
| | |style="border-style: solid; border-width: 4px "| | | |style="border-style: solid; border-width: 4px "| |
| Zeile 38: |
Zeile 38: |
| | * Ein Rad enthält viel Drehimpuls, wenn es schnell rotiert und eine große Masse möglichst weit entfernt von der Drehachse hat. | | * Ein Rad enthält viel Drehimpuls, wenn es schnell rotiert und eine große Masse möglichst weit entfernt von der Drehachse hat. |
| | :Die Trägheit gegenüber Drehungen, sozusagen die "Drehmasse", gibt das Trägheitsmoment des Gegenstandes an. | | :Die Trägheit gegenüber Drehungen, sozusagen die "Drehmasse", gibt das Trägheitsmoment des Gegenstandes an. |
| − | :[https://www.univie.ac.at/physikwiki/index.php/LV001:LV-Uebersicht/Videos/Rollende_Zylinder Video] von herabrollender Dose und Zylinder. | + | :[http://www.univie.ac.at/elearnphysik/video/PhysikI/rollendeZy_648x480.flv Video] von herabrollender Dose und Zylinder. |
| | :[http://www.youtube.com/watch?v=4OD4aDlAiZI Video] der Drehschwingung eines Menschen auf einem Drehstuhl. | | :[http://www.youtube.com/watch?v=4OD4aDlAiZI Video] der Drehschwingung eines Menschen auf einem Drehstuhl. |
| | | | |
| Zeile 52: |
Zeile 52: |
| | |} | | |} |
| | | | |
| − | ===Das Wasserbehältermodell=== | + | ====Das Wasserbehältermodell==== |
| − | | + | |
| | Mit Hilfe der Regler kann man die Masse und die Geschwindigkeit des Autos verändern. (Die Massen- und Geschwindigkeitsangaben sind in kg und in m/s und deshalb etwas ;) unrealistisch.) | | Mit Hilfe der Regler kann man die Masse und die Geschwindigkeit des Autos verändern. (Die Massen- und Geschwindigkeitsangaben sind in kg und in m/s und deshalb etwas ;) unrealistisch.) |
| − |
| |
| | | | |
| | *Mit welcher Masse und welcher Geschwindigkeit enthält das Auto einen Impuls von 10 Hy? | | *Mit welcher Masse und welcher Geschwindigkeit enthält das Auto einen Impuls von 10 Hy? |
| − | <ggb_applet width="1400" height="700" version="4.2" ggbBase64="UEsDBBQACAAIACS5a0MAAAAAAAAAAAAAAAAuAAAAN2FmNTE1MTg5MTNiZDY4MTdkNDM2MzU4NDA4ZGQwYjVcQXV0b19ibGF1LmpwZ+z7d1BUbxQ2CF5ERQRFkpJbJIOAknMLCkgSyTnnLDnTggISm5xzajKScxDJUXIGyZIzDXSa/s3OztRWzVbt7h87X019b9e51fe+oc9z7nnPec7tbsw85i/wTF5GTgbAuQcAONgXgFkC3gOPHj7Ee/jgER4eHj7+o8eEZE8ICQgIKUlIichoqUB0tFQ0NC8ZuVhevnrNQEPDKsj2+s1bPj4+EIuwuBCPGBcvH89/i+Dg4+MTEhBSPHlCwUNPQ8/z/3XDdAHEj3CicDtwcV4B94hxcIlxMD0ACKvnA5z/tQH/W8O5h3v/wUO8R/iPCbAD6p8B93Bwce/dx33w4P59bK8/th+4T/yAhP6t5ENSFRO8V85kPIGxuY8YpKp/katOnDLymroE4T9+/oKCkoqJmYWVjZ2PX0BQSFjk/QdpGdmPcvJq6hqaWto6umbmFpZW1ja2rm7uHp5e3j7fvgeHhP4IC4+LT0hMSk5JTcvLLygsghWXlNbU1tU3NDY1t3T/7unt6x8YHJqcmp6ZnZtfWFzf2Nza3tn9t7d/dn5xeXUNv7m9+w8XDoCL8/9s/6e4iLG47t2/j3sf7z9cOPc8/xtAfP8B/duHJJIqeCbOpK94Ah+RScXmVv/CZ+BVPSU3dZl4/JyRb53p7D9o/yuy/8+ABf3/hOx/B/Z/4FoECHFxsDcPlxgAA/A71ryvj/+n/E/5n/I/5f+OwsbDJiwxDeyzAV1XhTn3wtlZEhkYRYO7xkecewEFaanaD8dmOmRN+7nN5KQr9njP5IeeEpioEyH+hQP10lb1B/dkUy2/TY9mBFCAxnJFCgiYGTuhuHXOoN1RCU0uczuV8H70Uv2vgWZjyHz/eemcCCquiOre3yvSNxTIC43D7flsG/LpNa78Mu7dT6MuRqcpe5oR9QxBb//VFKM1CJDSU2p5D+/kMMBs6TU53UCyYdpKZiZ51+gZ17zgcY6+bwYGCNZ0CrsBcZaCxpG2syS1/5RnbeDidOHntxLMy8+H9HKujzTSNwwLAg457iDBur80/fG9Sq3KMjYjcY/ZwhkJLmqqrzT6r6pYwST1QV7PiEqniHqi7BCnRAhL1rsoo1cBzcojV/scA+B1c7sPGKDyO2SJXvImqgIy7gU5WZy4ouqQvBoKsKoKUA/Q2MQAp9XuQW8cXyEZdCXP8FT/OfLepEkUqktgF7kW4RjA66F935aPvrP9cvPNHwOIy6Iup/3li9GNileLHINaG7QbMR++ZvulxfjJdID7QahzcHfydGno7F5WhbS3NnZOKwQDlJ33Cvm97xQHMECH7I3KFXv+3QzvdHEVrzLI6CciH32LAQ40UpC+bhVJH1N8SKF7qqeJn2eZ8fJU9F/5vTODV+QjiTCAYUX/ZqulSsdK7XJIiZdtRK4CsdKVyB1HWmifBwnuDmPYJWVZzE28YsYzrntnSCOUbai8Xa58OUjNMqlEtkRnqFkh5ex4Hu1uJrp5q0cdSgjOVFBy1LU5VJA2VRKogI3oDYkkFuG/elMiEnA/2OQWVKFdM2Pcpr60k19r/1aBlCHfuIHy4+ZX73++KsbNMGkyVQoVaTLgf0RRVZ14hx+uy85moZ3Am0GktvgVpGT5uDDlKx5j2ob7OK3O3kPJB78VR7xWAXUM4AmQ3uw0ccr2e8J3R7xnzA4p/gY85ijKeu46Z24i9oEhb/pqqcJlbJ4nPZEz+9aS511/yWYVBiit4UIqOz5D7+lK4NiMvTfL7QeozvTGSdc+3kTv2t6VXujwGo66LBUkbjlp2c+pv3mrV5ulnSoee5gMecaZRx2wKvT3NRjlyPH0ZINqYI1dgQ3UyzCXUfCC9I161KBTi2h2ob2e13udjIfWmg/Ed/07YbpLC59Dtlw1k/p60CKdsdA4BigaN3s3rZAl7Cq1HwmR7zx+o7wtL8bpYM8LqdR7f/gtG+lVwbd0I7+8YSBzvNfOsHfHhnZrL6Q4utUXj5Jt5RDfnl4e9RpFI3umA+zNklsjNc6Kb0zp0dCclWWQjiBEEzQUcqbuEYGOWtezRi3LYoCeNIlqZDUkxvd+owUOfyoGSM7rn9Asl32WjFJ/UQNpxgFPhkm8OiBG/lzQ/Y3eBO2Fl7BAkXLcyPpg8N/7GIBXtr74GroBtlBy5ydVaoc0F9hGYQD7VMi1boZ1WvpTPoXxG5rSzpE5kVXOs/v5O9Pk4JUwSIXU6svZ9BPbCyL4O9Bkcl3Z0hmIibfcAFcdfIGPi24xgGEAcmU62mllPQJ+DOBzpIwe1dezbcnI9tVqxe65KCknbiID+aPOozKVUaPhs6e6sj4dVO3iplNTS2Mst7iqIEIFpIs2N/IJBrhJu9CLKKtvjB3dHjZR1knLHaIUEN+eXV9e5ude6yg7o1Jvpcvye+2DyutH38VjgLAcL+1dtIQ95ASrxIbdaFv5F0cubFShLzlwIj4QxwDrLtYNDC1Ey9fiDGhijyNns5tWKCouHk1cIrmhBEajsaGyRysTFbdUpr+Pi15V4vnodmnoxI3OtsVGBVU74i1Qszijl0fAOAyEwF5CSuNJtozxFoHKGjEAsaH61CJRM3OpMwZQTkEnUjZH1LXkYIDGcXRf8gmyk/h8UtwMTYyIj8UAJOuXsZ03aZH/XtA1QOC32Lfn31wwwG/3EqKKOQygG2MwBt5GqICuT23WiLeekkF16GhbxJ8vdCTjYVHCiJ4ul+w8Gm9qrWJGuP/ZK94Hw9GJ7krSAcclxUQIJ+W0xuQNLnnZyspvYCQCrRWBAXrVMMBPrCm+yncq1IER/N6vDnxarmaq+lF1D2FQo9kXibMnsnM2hX6y5jQJUFUnov38YzHYfJ3D50wGA2hMnCDq5/h5lTAd8xwpxaylEzxPTZPhDPIjwS+tDSKLBf+40ufgMNdXRLlkGWvCHdKLpY+Q1foECL0SeiKVGn7wOPt6mAX9nSMhtG+VnYLN24oF+SABnegC/tHxOpT6b5AKemQEnPm04tNPlvnfBdGla+phoSpX4RqQP1Sz1bO7XzcWj6XBK0/q0Owzv4nCXAecS7wcmGkHPsTfhjc6bYLxDH8qpNvYM15z0oEvmVDstNqopjqt2uQFT3EF5bOI/Psd34mxCeOZMfpV5QFxZXVRBIrrUNrXtsjaXJE0hmhgtR8Gm21SELWuYiDKOyAey/yg9hNF4Ywskxm7O1BoVZ1or+/ayn9K4XMHKi63kE+4Krpi+1TAl/ZnZRKp8loFtvTBZTHVQHoLSLRgJPe4Vb/nSVyHC3fNkvaQ92QV+xt5/lZffHQ1ZZQsdnEsWbVNUZHEuIwj0uSTVnTTqxbGlsbapvqHVtYnQeWvm87JSk9fIFpru3aFKnVjtj3qo0tdd7Sa66XJNC0Dpck+4/yPJnLSqtPcm9WNPG8ftHL5/Em8lHL85V8saYbbFo2L042Yi79p7SddfhuEdytL40bmVdUzyjtQpLj77dvcvFa6gRzThejDJZKnyiZHhtF0QdB2hugKWc7nPVo+X5NcTjg+rgxD5IvgTEv53LO55wmNnNnHd7MNUbmDpctH1HFMt4Uxlypolp+Vc0zkHqa5nqbUrHR3Fo0NIXLb4O58WCeWcbRYXxqIyknH63Ys7ha2V29hgK6W7N9QH6bpnKmj1d+SGiHgVs45TRdxBMrnaXfzcFgFp/aw69s4GcTYLlNZ4kyicugH+3wKp+bJbPLC0jpd5nTaUjqxPkoPdGdq+eCVgfxhtohNBl3vNfdWU6WLkluMdDmF0YngvdqdGavkkCZT/1eg2drt7+4+id7DZkU2VLwZ77KuCParZX8bFvk/s2zW5BUGtyD1d3JSj18cNzr+JudqY6hhU41fyVTzCqLvru/JlmwoHa48ofmwdipslxCng/NbkB+U0t/+vtdDmp2gZFLip7J0JKQrrPhTFbPXWwywRlnuVVGYjBt3+CWHcKdllGEddbTDNG2BoAEv9+0RrS/WZPH3Gvx0M6EdSZrZ+afPjbyvkW50pDcVYc21DY/mAotc+ov+bqFLyB+olo2BDOuEwFFeFYEiZo5PRYnkN7OswDVhdSJ0BqiwDUWrQ0FImNFZafeOr0JV7VovozJ68YgBA1QY1u7Kjg/ZZZ95ZD6E5SmwKurrliQJngTCQ//M/BkpdS3kz+WUvhRCdAUMvwEv82e/BNt4LSF6dsr5dgwoqhFd9mDdMsbvg9ilvDKo4FPN4R+C7qzRH0TDhGjMd/9oFlYGb4hCMx3SXq7suhtNVdh5iQw9MlS4jdWZ24pgEPWNAye6jxczO6M4BvrMSqXyYcq5eZEOvjQvkPQiy7DU8nN/C5Y7LQ7eUSdnxqf3BqnJnY9F5mq5cp9zDCI/v0CTjErHAOXrZ1ef7R4LtVw4yKVJMl/z9tQ4jJN34gXz21zWTz9XMA8L+Vve78F7WU6h5fuKLrjXp70z2XW9VVul+3mgqK9lZSVzuYOl+iT0/finYJ8ckMQS+g68riJXuNLTGjm7m/XN80ZL4bUM2+O3lGpT5IThlHL9ZOhqrWaJE7O058mMR2t0ENBpiZZiu59D3D3l05NfFZ9jHzLF0Ey7OLwMfgymsiPWakKt9qktrPb1asvG9q/CqDn+8tZgTYZb5vCqDDye/V61fOJR16qn2t2MRu0DsjvKiicb9B7BHtESN0X5y5SmEYe7fqG2Zs0Vov1ve7+Lvbn/GFaU5G867mpl/5vcuXfmWKsmgmPc/VpnleD720HK32zi/5Q+McDNwd+0zF53zx0d67MKpmy/t4LbOuvkoTlg+EyZGUsp3OOOzQe6/j55y4bdD6X29Y0VZWe/cYwIpX+B7zRI/Mo3GHamtqn+YJqQY21uznJaWntjuRw16xn/DgOsNFEnX5Dn9a1tfBDB93td6CA2y+v9k5Jzmeak0QF2RvvERzYYzcRLUS72vmZjHlkiIXAkgQGWJVAcY5V8qPcK9TbHkQ5Ug9vIqCZB2oBEbT6XEguhcV0YlbvGej7BEJWC2V7U+49Bu0oIJdiddCt9nxDDPMouMLt3sbylr8SqmrOqbim0Nfi+bZ+dwYasSmKXxT1hic+tQcilH4wTN0abu1OOMt9KmuMmneJI+jEALQYgGp5M3nit1ZDW2xjOt/dNf6+Pf/kFdT7lfP80hMD/Y6W3a72NYxTDUOac2vKlgTytmUL4HddzyQuuwyPxPsg4RYX8xdoDOw8XG4+566SzxT2tj8SvIr9ttfjlv6T7+2CMR9uMJhI+NLRP+ZFdRpL2iWututz/gGQfh7pFpjAzqHhfrquK9wwSJsgbbA+8yRfnyDkzrOHMtc6PuW9I822mHUx0cGTIVG5L5O2G0D+iRdnVPpFHXwiXqSNYYb5f4PF8cRIkNdxYPu+RdFr54kbdE86nb8Add0gNl+vzV/rccDusP+TcGnxNvuKa+WowlfMlj/BwI1rM/4Eb1Vj5NZV7xzdYHJf5OziXSOV6nETngNaLkuMX0QUhuEVTseE1jHYczm8d5rRwg1ak7mb5X4jOmdvQEjueqCJo7GwcLoby7+/SYymeVXqcZcrdJdmkwdqQlIvyCOrAhVNiltqhQ3OnSxSqpj/D4SYzAZtJHTQ9f3Ix2NzZInSv8Hm67NC7gjSKmfkH/T/5HdeUwz9oMp2uQnVcE4ddSkJUkMZTBiAbElYn59lKuaIqUebEj+DVUjW9USpshrJHTIxlbWxZ97VRNAmLB3NG1SV7Vuv9poyTo7YtPrZuNb24N/+kMe3SKFTkxcJRunYqxFtwGGDIgzv132nx2xQzjzpZeNjfQLr/WMfiF0onwUG818oWFXnlkjgQ3dqfsYFy242F3i7x8a1vndJdwmRppeVLXU80PzDeqXoziG18V2bDwWMuW/1A17cr9o0AinSbwQDMuc2hzz1BV4Odl6QaSvtP6MBmYnrBFd3xuPKE32lo2/d7kSrSPhPd2r0ZuQGtvpr63hdnGbjQbV3SAaYmGQxgzr1tpCMlv3hswXfi5ulD24wegOKemM/ccq55yis9pL3j7xRa70ytwLVfODASDss+KQw4uXhQwzv75kW791yYFh1T6x03OohjZnY5eM/QaOOitveFXVQBuxsGcNMw2fbWns3aUWrqHaE75mio8+6scRCo7o/pHGpKN0pDz7vfzt3Olex5DKKiLM6JrvCX5jU2mIZi3T1keV+TiiYRSkoUFevr6WdEd0Z5qmr3siBrf12Tg67VDRTdx6rZKNm0L7bqW4jQVQyz+Vmz63pf54/t/mCAWvrxu86hFLcfOrU/oX3Zs7Hy+WKH9E/O8wXpEvlUJOTe/Kw8QVA9sP+Osn1f+OEdajEcovP+OjR7mPBkkhl3tWDKNJFfVGnCRGx7l3y1MvXpsvd7iXpV9JCQafAEYOIMUoYHq7/FH6Tv8ykw298ftSp22G/c94FMMVV6E1Zv/3oZ6Qr1OX6d80KQKsHcImCyAgPEzObOXs7nTjiazwd8bidCSDVkqhflqSUWmiV9FR10+6IT+TV7qLxvMmRH4BJbGRNHGuob1WVksKETpzCAVf/48YWKak1ENW9iZvTza5ak5fxQ6/kgLeafO4GHBffvmZn9Au9W+OT+/HFqSq6s+me9s9ZLnp3GQvtpSLhXh46+vO2sVRYrD6ASXoMc+l0skdd6QnhTXc/An1XdsL70hS0SXyWEEbr05TYZlWsYYJbUfa6g06HD4FJURJLum9D8SXjrzocKXtI0DQWvWqgI/YNKnxb2ZJGfPc9dt1HQ738jKKIevh8i27e12KvneFrs438z7cm/n0V0xlR3XhmeJPOnQP6MiF/nk1YMGcnwxes2QaHPrheAmMT5dr3S8z6HptYp88XaMpNJAYehgPDbO0e6+n/Zj69m7H6ZFPMMuiwscGQkOn1WVvr9bXld2nsm93BnY3RvWk0uaxjLtGV+/V/NqqXJUilzHuSlfXroM7kbfQngpul+Jxyg2RJYfiBUUgyUUiWe/qz2DSV8R/9OY9mlB6dPtqrC8Eg/NOIK/Oot3mBgyNiVkJPU28RNmi3/fRuDeaUF/Ysqyv0RnvTBpSTLK/HxHbsRpxNzBnO/506c79BwyPDd7FwY/0xLS/zwbX6kiSvSASmMdFk7pdosapGw1Kip5uqRgLVCRC7/HlEzhMx5msNdbi/6rV486++TdV2eVltOTeglQX4LPuoqPetMdMLSEJpsVomVvVfCMTLCr8EVT5JiHVeJJLZ42c7NDEaUtJozRjlGfDNLxR/YrsU6wG5tzlOfrp2VO7Ruqw/oe7LcKypvNjOGlTUzvmOqwuUCMc7J5BI+bh42Ix/jYjAtcpg/Dq0wDNmx3kD1L5LL4j39OH476uyyvDIQ5zWY0WjKridMScYm9rAUA9h2jnkOQ+FREqLps7R6Z3zLOIoTQ5SfdEtXcljnd9v5K7kgYRoYAEel/h9aKCjbVFqZ4ambef23VduG2WIJ7wW1C/7j5yVP6oj1upvCGR+F45kYOqwTWB+3adF0+TVcn7CAV8cmMECuViFQEH5ePeWHbA9msw+DE05kv1d5qOheuPzgy8Vbol3EdAYG8EmzIPiTPZRihMvoXlQw2MIM7Io2FY3lLI3g70chSwLDhMiER1wIMQB+GYzbS4SORpLkOW0CaLIoymMQA9wbfdsyiD65LJkOuDirqsolt4sVzN3voFFaJK/GAL4YQKriG7m5l6VSy4Om/+08W1BoK8D9QgiG2OMWvP0eQMbX1xsAJ9+WEIJaRTjyIlVkIGeLV/UxiZvYa2AMEFujfLdOB2HQCA64LXjR5uoBxQCkHJC7/fyrKqs/XQ4kv65JEYlojY0kL7uBpSImo13DufXGCz9Bc5kA7WvUG2ddM9q81EIFRj2327B54LJ46Ko7QMPTzIdKRhP3GM2/S7FA5pcfnZBlJNyF3F+lca6b9qbcwlHe4lKthoJ+Kf3G2dOcD+wTKgqqgMaDgp8TPKNA62cEaGSXEmqH7IblgW+wfgpeBid+nhXAAJZNiy6GYpA1Oy2Fm9grGs3iwQnZu4BCDGCghQHe6cb35ECfrmZAAAzwJyleirUlumDsnZGwjDLKVTe513Ux+4lR3ijdddQ76hDlkfo5A7B9h/Sg7w7R187NDQywPaYBrvAowOlbDUjs9wICMICK+JsS5KjHiORt9NpQbQ8GeJaWTYz/WIuWLd3j0ti2Tw2VgWLrsKa9t9F8PCCGAfp9NPug6sFEcCYMsKDkShzLJzHC0T63S9VQxNfeGsc/ryZu4dwHWVFs3DT0pxKv75md9L/JKLmLfuJ76y5Lls9VOGpIZ718enSnp+/tydGBiyj70X9Gf3ADp/ur2Zuvf+PUM3Gcmspp5JnyDVs/EdI6H4WQDzoixIcGJA5OA+r/UdEdOS4ukAc218q9ou4MZ9ZcDCjdCnhyZDDfon+6o9d//qbo1sox8g5PofWFh+32TMEigYO4JOWTm2jIp5lCQ7W/FZZPCLQjfsM9o+ksNCL1adwp31VEy3gCvGPHvIYVhnZKjp4yWpJYSsrKmhcO/P9L2HAG88ViVUTZY9J/Hv3Z5MPhJJv/I9O0729ziaWjLPKALltOEA7eSzjZPvApIXNv+vN9xfQbJ8Oe6a/G/z2ODsyAF+aViI9kWZ8n4X2n+bij+tjnlAxd8Pn++UBM3+TH/R85SZZC2M16qkx3UzamZbxkkeLU774Cl/2bUokBNphbnYv2lB12e6kMdmhLg9OHxFqfixEl6l3cUd22as0wTjtZpI7hNht3rlyCEt3+hDRaieusrUjrRcTtv83Yqr67RoEztaIIaxmNz0ceAE5f2PX8YJlfwNtpp/7j91oi+5YdeMmUmzrZZ6IEQALIO071SEvl6ZkVLgi9wRjPwKjsZ1+S/XjvRhxwMHt9y73ggbHN1fzY1Jqec1u3W7NISK3+fKq1nZx2oy3Da9wP361aZvOUXlEyKGic6+FFR65uXpSnu+BeVTTxqCM7df8mjkUQ4+sK9aFEndGnkuETP6MpX7hdv4QVQ2G3A2VvukNtGOAuhFd7aOUD5eCtqaoPLtXE8Yl+AZ2hzlIOtpwCXL15OooFqHQbw3zGALB8kgGDvK/Mxd+YXrj5/XsTZ9iK38VfVqLem2mhMVF7XHmDAD0+lQHVAB/O9P6wsIh6+te5sRP0O1v/nGjas7K48U9vgasPczAqtGLFb0O7qP4JWY4xzwmoSn7J90Bbj2RFD1Y7lFdTf8AhdxT/KVZqSX+7IsMtxDDHn0gIKWt7zjYy6xnCRh8pR+36nbzX6FGpQmZ7T17BuKfgoo3Ui8+NJGZgX/BQLcvZp1D7I5rkSAMv4+q36MTeRVtTb/JYv59du4G95nZzD7iHOaCtF8QHOq8ZKW3xRXk70vt1aazlK6ZT0IfaaMuSwTNSZSH8whUJfx3Zm7mMQW++ARyzoVNpasN3Ykku5IIuPpoR+ArVnzKUpSA/vhpLF4BuyNZQtpVrz6q0/dLsH4uvRDnzME4ccimPjrl+oB9bhYmZlpiUwE6hcYwj3vF7KPYBUMfmbOmuy4CSzhgjujPY99JNaKeOf2fuKlPYrL66+fzvI4on4d4SWxrefrJVcvAruVBa8hlIospsfoqhVJdAf9iXdxu1BuYr3Y3bho7MaRpM7tOLUI6i1LaW1crqXcSnA/DVMgaI+pwk2tpMtXM5onMnx+Xyez6tsWCl35R2u46Ul3nmtXPtsrqnZ+DCIplJLAbgpHZGHvCTtVDZuHI9cry/nheZIdTnNc7vcAyrzeiBw+UV4hsWFWEsYn6/LwtqWpsCl7bxOogoK1pZy92lNHWer4wR4PUR1T6NuqIwUUjaNnDnc9tzU+iKNbQT+a66ab36BYZ+kISykzrpnn1KJguBABZDimOMMshqlF3sLB/kcO/i/oQyrjGU612vMgwDGDb4MZWU45Tz46svDPfNOZJhgEAUEb9zUXx9mP9EaJnNlPV56cqg28ACPrtxWUCb/6PyNZElBFwHjk34VJdKqvuTdmwVIzHLOfuCJTwsMMRvWt8zQ0/XImXa3+XECow6t09XV9GXMPnxd9+rWmi4OGvhlZCTROxcz8UcWsbWfuTDXAOBmyxOZgzQwS6ZbwuF23NR/wuBLXT0/uNYkfJRcL8Jxo6uzlcinnt9ep50MYfTdXU3bfY7bbNquNAAa1H9KIPJNvHyhX1NOK+NVgSVfHmPVP9X/+It/2/vrXQWUInFBV+PEPpigePLutvHDPVBGuo2gsaC7Bylc9jZtfz01TPoGWL2fY3Q47li8SfOlmwrv8lio32O+Pge9x1nlsqZMEY9WRltijFpy2x2qrR75xW3iw5qicEAX2UgFcacbVvOhDA0YLMxuXXZgCUoS8wlWx3/PKKuZE7PmAYwQEpH7k0v6GZSesP/nQKDbKmh0Ifl2/rIrx3IMwwwV85r5laqU2GlcayopMUvpJSV+SS45W2SQc2KyEVzZ3BABPJfFL//99sXUtQOthvUg1y9lzHLcSMGplqMjatiWaJEY6WGy+kRnQ2pkX3vEYOPHwz74zWwe/kJFi8v1e05CADdX1OXV28ZcFGVNlN7vDo2w/ePQza0njLIrGxHEg/SmMdPLdaH++0VsLmcRy4yByeXHOmiqWYKfraHfPl0MzaL23TMwSflED2y9ZX3qojD+4VJYPcg8mCxvnwtX2zBthxqm/2x/kyiIm8IEckjzVQmckUt4W6CJYMBHOWNE22STg40b7waroKcUx1ME7IgbV3VSLkq3lOjH0mTdubNMZztbbnna92POLKRXtAeH62GX+5ECYVGX5xSdT4ay1Z4X5W4yM9yJWTUf+oTvIaEfd3tVdtd+xQKGgrEEjz/8vvSpTaN0AN3ywHIWR/uZcVaff+xjcR89jI4rNxby8zBN6XFo2qj2NG5fH5vFIcdV0f4SZzzxGKFcrltgIn5lNM9DODOHAq6OR3VbWki1R2keAyjoXETlxbmHvlRVf9JxsaF5U+lDVPzu/27akM+xF/IQXvnjdqnwvLNCA4MgHzU8N+XZLJH2Yec9C14Nw9Ui1oJsgxGwvgrZFYalvX2iWuDXvXEvPFAH0v5dartqTSGcc0IUtQzaadb/GIGLTcctSEzqt43OX/LSoS5ae4v/OUyW4kUEWSXHDA5fqKGYKoZqaHMKI4Y8hpG1nyR0VsjlMUApcFKHiyLCs2fDxa/8jCvvD96FKT2zFru7d+Mb9vGlwy0rlcw2A9Hmi5V3x2FDFQm/H0oAw1oxQ+GJyQROpl5zXpf4J87/nDXgo5i51s8SrVb7g02poba+KN3qwNloqEaROiSRschtNjmcniVBV33ddyxaltnyM6YUUOUpjTJLU/8qzKZnsC6YMlgpoDrtxfH4481jkrlk6Z02sdaarqy7BLjmGOnnFbf1+4MsAT+qTLT9EsH1b0e9WUI2B1MJHB++YsSHMiAvr0sfpD5o7Ehct/zwdFyzZDRDgPI7e4arJImnuBLtDjczHEQN3b62ie65MUi5XZYjN4hR/9gc57Q0jwo5ViYhUbAiFxmorwbrvpD8QMxWzhpGN79n0uJwnQFfivswvZuczoz7hwJJMM7X0HHAq79tLxZ4gN3Wk2TdXuLBx61Ps/3wVzvagBZigGhy6txSaXPUOPryWOJ3b6f0navozy9a8YF4CwDBuMMzlniouRdBwqC4UkGShVj+e6EsV2OAr337QUyYmT+eoLWu3adOvmT0NRTdHvmDiqr4Nfl1SIWFva73r8QK8KACzvRjXTddGMYqV4TqTTzdhNbMkfGodMJ92zDNTbQFsg2Jrv6LPU9+3gNOuNrieV/1PBrR7fv4TZNNX3IrERo5zu2Fmi4WcdUQRKt7XWPnv4PmJ0v03JFs3OTsD13p6KVMHmCGyeLoLzTzrNPbTIRjYMOTSuU+52fEj0e2TvAQsw7E4bI4za3PzeyO8Pnio4lTq/4QVpQ6RtIF6jRf6L6abWYT+jCWOHrKaa8n2FH+T35LPB8u6AR5yCcfuUEtY0zno+vmfUGVpxwH9H8Djb77QBu77J3GxcD+XQvOdHg0+gW9gRI/8pa+FnQgy8MRRXc/vh1jY301y7pW4IXnO0b2/kG+UPxFBcM4O4V6n3x/YBKBNEBnWXZTYbMhf5g8WE4QaDTa8uFd1E1WtnZX+7HeLoh2mvTSbwyN+P2ScVk7Kx7KoOWWEwoB+icRv9cXpYrN0hZNmae+A1qEGoJ/zDd9nU07DErvnqVe7Gh4GUG/Zwi58B1YKNokkqavdIIT6YJeGyD0rl+Mes3VrnWM3vCWSq297JV6g+ZhkY8xRi1N+2dO4wlgq+xMRoiSCwnGEORSBGfnXDxa6Bf/CDWLsKVdvqVzX3SzLO8PpzGeJoauuULqKsSQp15dzQWXlBt3xI6gMMsPODn4egDdZKXKF57dzeeuiC3ESXA1MpJ/8RSUJ9L620lrqPY5a+DQ1uZM9qvbc9z4SMT3hPfLSTMvRlckMuR4X8nt81ClgTTK41F/eDBrnx+UXFPMYCRbXDBj/dizgbeEHCqNfrjisOAqGzpWSRdP5m/HBZQsmuN0fOlgdlaWVfKxhb/6oB/fruVK6uWuMZ0+fWfVnkn86NtDLa0/6a8530G9tj6iuvar6Ivl/U8TcpAkZT1gh4/+AIH3Gb0fvwfO8XWr8DCVEvjLIMxE339yocERCeE7nB+2HRMR53nycaKgPBO8Pdua7OLLPF8euHblnMhvgGkUWHLYiBjHHUBJ8ErZwGRo93swi/08zIp2W7V8rqUhC9r+j4pKu2LBqjH0ZtnMvC8Ehx3+tHc4N9069/eUecvQ3/V4CN5xlka7VCF8mowQ5YJIHpcRHBhg5y1x7fomUJ9ReroJfmjvZO5A/3x68wJ6RWy4OuonnuCIF2TzjZxEsnbKW1WOFFFR79UFsu0X3uRF5XyCcTckBVLcmy3G3/sDlysstB26+jDLtT0XQ3W6CJYdpUuuJdaicrU7iJ9Iw7iDj1xewVsB6n1F8picHg/nhHCEYMHJ1oms8915BmdR9Z+b+nL3CIH+HcOGz88G2u65PycL54xSBzHS71rJcaGPlL4JVsQUu1yQDrdV+FoYBbLRR87+BhKYL45BXzTfXmWdoECa7Q1LhGWSzXS6XfyvLmszOUuOs+3nvMGHdCbJeOCuiARFONi2babZaGJAm6TFZTp6uqfh2nOXle/cTOJkVbQTn9ApvLu/63wZUlzCjJ8of0o0c6KU0HS+nCXIduWQaqt1dF1eqMAF3cyZaS4MOVrjnn8n8+ANnuSKYDLmPVWezGkmTwhmHzORfAE99Q5ejVbbe/PLn/YhhPV0jyplRXzLfTpHpLu99pq27neQaaUy/nAaFM8FKK2b9dKFJSo7OPDEN3A+X4luvzSdRNcJ/+Bk+rlP3+IyOqku/m02RePMLVitV90eW0JZNEvFQg3C6X5D6tZo1l6vl6h17F5sr3Mdl7eVvBTn1s1qUutlnio2vTlKJum3tL34HlkDigT9ZUmLa5ftbGzkfSDfIkDNise9XoF//7IFTBTZvippvPUcc2Vu2gjYAPhfqe21tdIZXsr4qdg+2irIB3LutpW7JIo5EZpSXpkWGpWbb8sNBOeFRPEmcc7CeNSbLeYX/bLF4Ij3Q6+9CSJnbU+AvPY/apEKhQvx7es9ymfnqWNI94PLBXGYqlNrrFpB7P5maovw4rlTXL+b/jPflTo+GV5xFqER6D8wuKAHmIB73YuDt8UF6UYdSVUEIcYxqEPIub9koPsebpTYmLDac/tIDh9zHLzHX4e/2WyQCW7qcbRUiIrXNy2rkP8C2y4RhRPyhy8rh+pBbaKfBBO3u+xNcXltGpNK7b1i6JLd0I16J9CQmsa3dsz0tWbgPuWEq6tNKB1tdi5f50V3rUNynt6PiPlf/KeD5V87gyaJaVJG+1lyXVmisS5X5OtVHbFn+NA62a++MiG2pfQ40ixscbbcPEFDgPHTqsvCP2z7C4KyaPHKDAaIzNxmBfYyUBuakKd4dfjAFLr5T+tLCWith00Onl+ZZAZpeEx0pPh3CunWW1CH+fUVHAuoh5uALNOE3jwzmiyaOIkuG6Sa3uB59aFwbnZ5ZHw1UDVx5qzsgUdRrBpY7rxIuNYH8MaLWR8Nq+C2zr+fZT0i5LdhmtB6MvziiKT/ep4ves7zYrdX6+p3NdxHrmdG+Gh4vvf32mpS7xcDUyYOpJFjPXlQX7o1gaRcAj113mXJ5Ffs839mK8bvjjHAOarPDyZQ//K6qunLUINQ/89UQaHXuktKTPuuTxUQzR6m933sXpyo+nXITQb+spYPD8QUqHuRH0T1k9qEED9PHtG7npgrxzJvcFYf07Xh2fQ6jIFusFfV2a4S5toOF37MbliYlENcAnSHvU7fUrcdb2Z0scjMRyDIYr+4d4+Ho7vvSvv9MYWf+2iVIWSXLlHNC10+ZC//moqP/o9/W2orDxIxIyvxnl8ItEB9RGep8NKbU0XTvzqPNESqmXYqoPqYrBNrvh5nxrLPqTiw2IvwsVS5VJF4zD5i6pni2xh/1/ae3OVjY0NYvMYoDsRSbQuvOR31yJ8JSiHet7WidBEoAPATGSdi1o3GABawqpuSnMh/s6Locu5eMUPGr0KueGUz6I4JQR5/IOsqYK2DTVQ+f7Qm7u49GtEH81yM+wwh8smqx2V/JdMsmOrQ9Q+tTO10qhXMIusvtbaTVzI+wgDcD8tLwSvqPZf8PdQl4Uc8KLdCd6aJTEi4pWkWLlZ8p8RfujaLFTs30G2THPCiSYLEkwS7sJnCVVFOwlu4j+Fj62uIpR+JlbAuW43CS1UXcdcByoXuZ/dMEvfIsGA0zUJKYrj96THx8W30PR2GeqsepfvFs0EqfbjHiKdQcrLf7aw9VW5VGDZzTv/NaIRyMmKl0v1Fd8afz81dFfl8CXN1LFv1fVJ8FTC6WV22mc/6fVfGIDnAgOszZCvd7iG9l33z8YWOp0I7irPd2lluy4ThbcJUo5fPwUfrUvj9dPRSvZF5qPXOHrIG99c5vDEyf3V8GWHTJm2IbJmA15aswcYMNNftdva3ETkRaepg26orjb6FE9zjH3V/uRzc/HeqhyWXCO1fVHjFmASPmy986bVqe9c+bQoO0wEjLp3iAGow4guqygzcujVWGiVPlDcTRzu/T8mWDmFiSg7cH9C6r7/KMFk400xxfcTvOxi19eImEpsppm6dkMEvBZHY4DYtX3dleDjKt/i3pJBc7gLnnWuUYKJFAbwFC/FKdHznDseuMMA1/x9Hxdi/NnwJXRRNqVunYn4LdkjY/N2An+dq1bNFv57+KwkMvpja3/uQ/Y19EbrBeXWpKirLBP3ttEXQ8jI2JiBnVLc3KBv6pYS4pcwI+iTkoa/moIw4xgGOMXRH6QIk938JBnTXSIDGurYMBK84P2yn6aagQrbulx2Rpa2LQ65Xut9CIOekTahyWOWH1uLzXBp1BAYeXw6Hk0yVaCT4ycbMqSpWqWBVginM0wdSMUGEfnQlf6uj1JivjDRQgzJUBKd4U4HiM1VU9fb2dn941KOZVSopWvaaaOaff/kd/887e89w6q/dv+4+ezSuetlkp2zBVbZXpycja2dFru0Od49W7fRoWXfh5tbbZlcMWAAy0L0QgteMBR9B0ZqmIz7u+Oft6X8qVIdXi0VgAmeKVNI/EkzHEPhXyftu41XGPAkSmjjdWyi+Rl9ekdUXvsqptB6mjablAz5yONfN2KAw1Idx6JgVR0aXMGX3r5QEJSsPU5Vvpc9qjeT+3pkF62ziV5U+1QmCrkHWXMfiVJBiGB9EIoe+lYqN62Ih2rFAFcHTmbbt6kII958kcjdGzWskx5MUt9igJbs3bNKV4Sq0e0dwx4eBjCEHslBdrFb76QLA1CJRxxyW7sxX0M+IDvvLkOuIScsqAt9+DU22V3crMF3khGaf4lu7lwxgD22HxVPZO3kX2mGNDstECTJ3uQP4feF3t46Ia5Z0fPNoPNzyMka9hOya013ZcYz6dEMkrHtutUYoIFLGdkGQsAxwFw+wvAAfIABzkH/qWL1ciesqg0DTMkLxiN5qIbQcy0YIGsYA/hRgeu5oMhGZcTWxCB2UFkrOmUAQiqjjDyFjNV01h1DkQ3KiB3oEXU+BuDUQt8U/jeqHB8DZJthAH8qg1EMIFGAAbqizP07TtA+3ChEztoKZPwDBuhg3Yq5ja1u7twdhZBA+pJ9IeMZRhWmGMBaHzsTfLLCsnQM9RpH3ouWofm3uIo1xC7e9n+ajyTX1zdhA8bjXoTBXB5k7R60wQBSi9WV6DQ/NlS4cVc/OvYd+O89qMABIpbo5lG5pKebLxSxpYoqOpjDALRkLuCXu1cCbcNYlcX6/7KueKKuQImm1BFVRpNQic1mZDBNpPBEffpvLKKvSGnmpfxZJ6SXJluS2pz7S2/wUv5Cx/r4lsNh0wkYLS63PbrqjNV3lstc3G/IINpX7nZq6+IphMFuKAYDDHdj/cNt6qHPMgz1n9XLnel8yrJLCt7CkBdOk1CrHZrx6uqtHqJRVxDqSmXcwYmzFbbEoMXAKivkOJPECfef159KGl0qbMvWFX7h7CrRdx3rByd+h7aO9RH74BIVbVc39RAxn9h3My+AT3noVcnwYSppXDWwEBJnbGGOl0j5m+hAV6C6IflMZJVDYZOzYpI3ZdEQWPS6203bqBg6zrvjLcqcKUDk//krx7DMnD5ixvBM6qg7/hzaZWzVuae5n9lkbRplmZg6Q6zdKLXCm7WVvafFMSTOIKDjTl8uFfuL2mYHnKU0/+X28rL/ooKdNede+P+ZsIlQAYp3Z5KUFI7exdcCp66RdMJHap/vaWUiJc8I9goW9RT7bIgVpPtmKIWcSsaVje1yz0AR9nXUbOaWJIow0z4Rp0vmNnND5TJb1f0X9gYrETgnBwbzYmC+5q06WWbmiuTXnhxsnh42FMmOn3zSOu2KsVFlmOKyLEamVGwyYi/DrUCJ0vGb/us/7MR9e/fiIIU+xwWcJbvsLspSPbONP5ff7y6JDIqcfGMkX9jnYNGaq3Ar8jV4Cx9FapEYJ17hrq0Wzl4hokRlQuVfEDCW4lvhvWISD7zDMXR35uGyTBx+jshxt92I2j1R3Lfh6HsYYdB2nnyhwOu/YzbI/0r6/NhY7u4ItKlz7UrRn+263Z1y+7mBbdLuDemPlUKnj9MzLTklaczMuOwDnYH8BoWJPkLIB58RDlttFUV48AJ7iEjwbuLghdML1HAARBdqrUVv63vCGcQXObZCLMyXHgkSq8lrJUrPbj3k4Kz8blxR4+19QC/sejOjzOGhzNLJnFzHEbNsN/ypwgWsJj/3fGN0W5aL+jHsz1X5PYaHBQlHdVFk2W0LKDZfmf5Bkzm1VHIc+820kFlSZ1caA0FBsHyEcFcFAdPz2UlDsFEzaG62wJd0X/DDkIrQfTOofP5z/OVl1iLRE8vY1sui8izY44dCJWyvDkm8a2Kc5/jl/fDTCgKDtueK/1p+Ix3SjvG6zLUXbNZ3LyGo8zpf6bqbHYsteu9Mjcp7vVukF3tZPpwOYd+QlnYoXZI5rhuk4LLo5wGjLm0Xpo+pxINDRJ1HVRW8lV8J9Oo2hGtbEHpsTkRxLBVr+yh7fvn9hH63UX6lKXmwPvYch+Bu1v6tAs5T88fNK6Fiqisrkq/1mJNdogOknQ5k64P2FWAsf/ojkxNqaVC2Ls7KehHk9rKkrT6OoE15p4WA7SCopz0GkB+cDav5xj6En2IKeza05sHilBevMli5ynDrXMDqe6QbdhUB3zzigXTJsBu4zxc+NFSSuLrTHYW6vyqgstj1eiO+InvBH+lYuSVssw2Okr4Ow0dckKKvuJ226EbW0EMt4usqJyJEB58MmD8Lp01Dlj7bZeuYm8rcuoAX+c4Yf99s/ff7f25HBFHMKnrEEe7x+582NkXVZS84RzeeQQscIYUm3lOCaiy7ihcUGCAg1OCayNJJzs4yttr/faO1ku756xn59rG/orfmVNspcW30SFvViwfsZYP7Pn+qSd7tFTlR8P2VsEN1noLQ7S8jFPqR38HyO8gSIg1hmL2fW+ndSO9h7ET2YTDNPt6prrEDGQ2qQxlxDelu3qSu/scmVrQUzeZv6v974cMe7j/jY4RbP3oh+7SI7+4ZBkhOT5IYxACz5U+qvvIAZFk647qGq/79h3mOESsvSRuPHG6J9pQQHonItwaNSHxId7WGjt6rZJvBg1G6RZizr1DaDgZQMmyAg+CnkGBclankwsJ+FBK0rt3HwhKY9kVnGhAhUlFeUj+mG3pYMn05cmHlnH23D+5OsPWxQt4uQ9bW0eRxZ0oMjs7xlzl6nbmwI1s4kRWutq2P4bE9F/j0JeSM76x0j3KnexcD3MOmY1LtNcv4P1NJi4qoVevr+vcLXUsOavKEgtoGVuiO//olZ/hq2rT1vxIhkURo5uo0SgXHVwmSApMCpzYI3Q7Il/ZMXnVbH2uW58m46EXoaYGDrNKJAzYzQPBuNOUakhF1RYtqM9bXM50F3FaK8yJJWc7oqC9Cm7tkV9OXy6TXevEHYS+QHKDDKWO/TPGS7sUvT0m/HWkc2d2iuq/dRt+X7LGgDSqxbGEfAwSzTvNV5q2eoNHcN5qyC1bobZBFClFruHgFBNyKBnxFIFMC1KqTyqtBF/8N+ZzcInoZfgnpSqruGOTOLXwejxtTEMCHqoDs4dUWrp3xs7RMehZU8y8mCrEPwNghVH/qp/nMjdds2t8fbD8FM+gfJjls4+7cG502oyjuear+DHZR7M7BDLZSyp/4e1Zf8JH4im1bBQOIV5xDRBLb7AoF9Wrw6u5DDut3shRXBBp3WJ8poKZuww0nG526DIdS/41ujLJ/koG5ZA2lgO6e8CPVTKeWMEBPz/iz+29jyDmiU4V22q4cYHgwtPjH2YtLhqx2m5b6xHTktwXVeqiCBOeErEKXck08ii37NMU6B9I/vLtIYjfaWzi4h4/sZa1pRv8FaZFXNVTeBdz3pTIY/yjBN/EVdywZjaQyulGqw/J3TibwdV/b0qGaDwvqShlxv3M1EtIVRTdFPC+eSDrRH+32dm4UfD2UiQHwj0MXGDFAp2XbEkJ8XCcflH2jigGsIFND6EfWOz14TAx/1vrTBLzkoD+jY7wQMljWxItN+fy7awub6AAsXQOw/G8ClZW5C0FsYoAq5XRilLYwG93XtWd87nuEMDSOimCPOG99ZP+p7jqkdqP/bg/8gMw/6Om5wp0KemLt/KmuePQ/P6lJxPxwNvwF0hp794MLPasTIF0vMEB4JYW2npnof3Gi/0YVFTLVmQI5ysEAjz3L74JLPERjz4gUxO13QB+xtCc8B1s9yoPPj7A+GfDfeSXoUGAlFoqqg1WmU/sv6VD/G7FZbPxSz9VvhwEI8BSxFM4OirjuRGrIrD07hIQM/UWsy15VavAJGx3baBFdRr/XJO2+y8jeR4r7YAAFHSWaekiKUQtaLQdMbI/QHseSItYiSHdfA3Yhys6Teqxao9BfAS8hzet6WFM4qkKCdaBdhsz2xOu+ueirSnCmEgy5WQ/efg3p7v9++TMddDUD6U7wk2k4MXuD5a7YSrpnShZLyki3SNexFSsKAzBBUmGQbryNB4O+HKxYs7c1GqHSMgtnTeGQBJUzqj909sdg/BdItv/+KVmOAXbHsFuG5UYNL8jdAnHxbwJb0JfqQVFpGR3Eze8Ro1a/w65mGMDDfHrtysPI7uFbnI5Xv5ACL1gOeDDAGd/vM0LIw3TsWo1QdDcMA3y3xTqGzgb0Kf11OycyLpM5wtgBWdJmkXNrvGtLmYIOU1hBY229VCh59tQP2aKH5gWhmbP8ID5aLnvfph56YO3xPvfG1dGob5bjoGYWe74grVN/uhtSFGtGx/N6dGp4chubrFqR61bIQpOzewjQOT4eeqnxRj1ic1SuGd1HAW/iN/Un6G6YJHN6ts9r1uZjiYUEbSpQEv11+3JfZAlFH4j1QCiVJww5fvYw+zwPdPOJ/xV468VjlOOTVzf9GjHIpOfeGKCyElJhrbOHftrUouD+rae21U275132ZIMbd6iW59O1RS2BO40msKfPIBvo3Rf2eFj72oZCy7/oL15lhvsO9u/g3uCb0iQwuV3ll05jo8+EodiyrOpz3Y3nX4Q9OCV58vpFshclBnB31hM0pInQmLT4GT0up8FWT0cxnYIBVspXtLkwgLc8rxNs2asd3Vmmr/syaZ/1mkR2Ac5BcxfXHy7GW1Kf/eM1V+b8g2apQ09Byl0Yyz/2larv9a3Z5Jl0ojIkUreZGbThmekSVwe6TqFuoMesbA4P+vLerW4RQmFwvIuKbd1noa+0mr8XD7nMKVC/6S/WX7H9LB8bwXYfYim8jMPg2uA8PrIMaQk4IW8k4flQOmbw9ZfZajOCzbGeo8iVLwJEncQmEHhZ4V4bzdrWtDS07AN70F7jYjeU4ZAvms+xr3M+N3w+sNz0i9A19uRAWeNxrjoAdOHWC7B+l6vjbWx9y5wxRmbxA1doJ+ePP3m21+kvVyu+uBrB1O1X0dF61cjaG81ggExF+v9VUkc536qHmjqPAiKlRoayZtYXQzJkX/D7lPSqaG/SNxrVHQRm1w0oTlXkzwIzMjKXv30L7PO5Epko2FeSppzOZnR0CWCZXdKfNbcefMvxLIXWxRusatu4+KQ8QEXfAX6i01C1RT4vl9iykXRmHv0v94GnC45wVQBxuLw4EbNDu1K6v9yCDsXX0BPTdNrzZcMsqQ8RTfFIdpHsPf3KspKKAksK9O3fBl/P4soq86lLFQLS6/SfdMrXajeaTWekqsmMAVZKj5oqrc7ZbyJUQtVmYGlMieRL34l6rV6/TSBVHHsh9CCl2innsugXqSie2dd+xxPJ5anjXSn5PNRfcjw4KVLJzNy27o/Pqp4sumiUtrOTmzmsnjpEH/9+wIBAeF4+kC2f+oIjwzKoHDwcZ5cQQgsnGTwPlozTm2zHU7hRqlSApcLSxiZlKM93UkKcHMmmwQTG9QaW5+eK3tenUEZI2xclH1R7WNa/gcn1VJd4s0ir3N2GgLZT32A2HWtRNwnIHPJt8T+th+JSCxXp35piBoZ83lgc+h/Q4LzUTuJxnVttb92QaS3o97Zabw+ya35pnuTQmoXzS/GpSOYyXV+b7SS9g88EyUcgYfmNR5bsngpVMgH+NTEhN/3jgqeJUps7YcC/b/H7Sna2PIcNDIhlTZ8yZYYnuQyrOAzVZVKUFiQnF4UbfLv7Nk5ccR4fNw2qX65DKpReK7NGL9L/+GNGMGi2PBucHcLFRF14/lf5RF+CCHUxG59tUgwX3vDM4J4Krx0cexlJxG0MQgjOtjjn/fNoM7CNG5A91evB25/R9arT3yDw3THS4QJQ96YvJIJ1KJzf7Qv/9WfX0FiWiyHqedxkXz4oauyKvgwp/PZR5xPJQvpevMLqMRVZ24xKIE8ANkzHygvvnDHQ5fGsTTaaThgQDZswvb7Tnx9J4gFELws7Dp+aqno+Y/agaxVB1+t/WXu9TzRddVEZeHSvcehcxh//CbKX/4h2buc8A1L/fG3a6lZdxJMjpct6y6TpNlJccpktgub18rps8ah9Ju180kdtYqQK6Ny2rUGtz6OWAwy3kqq4vSp2W+RI5WEtp3nyZ7TJ59uHhria9eN3V8uXsx83b81JlkiX/fYh45uaDocOmZ5yvIJNAWzsLsZbsSqcDhtg8S6nvLSYdD70C7Obx1OIJ+VmX74K0Q5b5nhrfPnp9w31h0NaEk4/87GUUPZYh9c3c4am+Gg8hoEu43HN8eisIkoJ+CpznC1fH2ow6O4XLqk3Ibup+vrpyuPpmgd+wZtT4cZMAXWo7zjq9kY1g9A2NihuEc+KrRF/MIP8bqV4SennQwnvZ49+l7G5sPdepeksp3yPeNNlvK93H1QhlfFReFx8v3eBWwRY6GEHq+lKZYqKP3JJhHMAoVH5F7CUP5B7G4GUNJNxXhsVUrTBI4jIRdFXU4k4ZufFSLYvSqzUn2ybGeb1R5S+fut6shT+uSw6KKZBiVNCY17L9EhfrYsar9JW5OdXMrrpSSkL70crkWpawDmrU1tAnVtpDXkvbtoX3MUYtVZVigzLorCvjtLvlIT1KEqJuUFv6DoS4C9fuRWFyUicHMim97ML5Wg+i00jcKTo32KDxSsbklYK55hv8EhlXBeeD75rbZ023cSjhm5LNvVjj+qpz2lMKRF9qa+ChQYl6vI+y7hOLSaxRarhqzPwZAS+Ogb94Osy1uRodRo+0HI7koCr/C8AbUCSv3MVhZ3F03fyImfH5cCt+HxVoFhbxi18ORy3IQbp7xhKd3fAbKgfRaq3/wAR9TuVEQih2KMKrFmVfooIUflXPOtJbRNY0092dF4f8JW0Ol3sOvvBazXBKp84keMdsqm7Fed3lubLUZ7VnR/LYruTo3PUVpW3i3VMyGbaVZcKI1Ee0/gOfzrHlZmfzGYlieST1zWNPnd5SRc3FWSBgc8UihicD9ad71GD+8I9RWtyLE3lShSeMD/bFMXLN9aVfakTO8H04pvVWBaMkDAjnI4qxZHTzdp/aMlwltzua3QM+fbNV3XazD0NM4q7toVrM6b7R4DjX5v7fcn/AG41z/47Tf7Q8CqxX+zdckYc83iL/wCyVy8qA2zsB8yYcUrhVuLaQAYkQg+9YuM7/EWnHsdIdb8FJHvTw5qLj1fUD/RaD4i8KxuETwgTkceZqEv9DXNrGu67gxx8xX8RkU0sGsYJMDcrjJ9iMUuWfWT/AKY7rsdJ/wAJVoQVzF4LsMp1ElzO3/s9IfGVguwx+DtEAfAG5ZG/m9YQA+39BtljHH6GoRG5spY9p3wPnGORtPNJwl/M+vVgmux0g8bESGOPwt4fRgM/8eQbP51GfHl8IRJFougRqDzt0uLj81rEcESW1xtO1lKE9sjmmCBybu2CHJyyjHbG6h0/N/exqXkdD/wsDXVmVEg0qPcONmmQD/2WmH4i+KvKkZLqCNoyQRHZwr/7JXPOHNvb3OOFbax9MinrE32yRCMLMuV988U/ZXFexuv8RfF4ZMazKqP02Ii9vYU3/hPPGckrR/8ACQ36kDI2ykfyrnhDI1kBsO+FgWXuB06VZEMnnQ3CIzIRsYqM49M0KlF9Ow3JovTeN/Fk1vHK/iDUQM7WxdOO/wBaZLrniN5Ilm1vUSkykxlruQ9Dj1qsulXrG4tltZiTlozsOG78VaXQ9amitpYtLv2aMkMFt3yM/h60KlHqg5mUJNR1aSGV5NSu2eJsNumb1+tRtJcNNEHupWWRTjLk1vp4S8Qy3NwBomotHcKSGNq+ASO/HrQPA3imS3j/AOJDqAlhblWhZcj2zQoRXQXM2c3skaK4BlYvET+VKYgGhfcSkmVI98V1beBvEEUs1xPpskVtImXeRlUR9jnJrGh0yWRYrYHzZEk+UxDeGx6Hv+GaTjBf15jvJmd9n4uY95LR/Mp9e9OW0eRLaZFbY3DE8AfjXZ2/hCdZDPey2+nBwAxnbLnj+71/QVejs/Cun4Z1uNUmXu/7uMfQdf1qHKPRAk+pw8WkmVpIkZpCx+QRIXNb9p4C1S6KP/ZsiAD79y4jH5cGuj/4SyS2jKWFvbWUfpDGFP51mXHiG6mJ3zyuT/tVOoy1b+A4bbm81Sxt89Vij3n9cVfTSPDUAHmXV9dEdhhR+Vcwb+d+nH1qWGO9ujtQufpxQDOqjfw5bH91pUH1mlYmrQ1m0A229tar7RRdPxrlF0y6Xl2jB/2nBqT7Pcj7k6qfVc0fMDp11KRz/wAfDJ+G2nJdO/WSRwO4LVg29lcufn1CVR/sf/Xon0m9P+p1Ocj0fH9KL+YrHUfaflG1Gb6SuP606G+vLZlkihlQr0YIp/8AZa49IJ7Xi51XyG/h3J1/Ora3rRIuPECu390ruH6Gj5h8js/7cvpILiB7maP7Rje6s0UnByNrKfl/CqsFvrFupaw1iZ0P8F2i3C/99Lh/zrnl124X5Q1vKfWMsv6GpV1y5Mi5t4fl/wBnY3/fQxVJPoiW11Z22m+KLmwKnUtGLgEH7XYSGZFx3Mfyt/Ouqg8Q2WoRefo11aXCucyBFw6n/aX7wzz1Feb22qrK6NvYSf3JTz+DDrWqbKw1Ng88REw481G2Sr9GHUfWs5QV7spNpWR1UvjHTdNaT+19QiDDlII4y7Z/4Dn9awb3x74dnffaJqZuQQVbBwfrubiuY1fwdexg3NlOt0o5IMeG/wCBKOv1X8q5Nr1LG+Rr5JLeVzhSeUP44xWbTjLmWhqlFxs9TvNQ8UXWo6rbTIfLt7Zg0Y6MXY5Zvz/l9a9etphcWsMwGBIivj0yM187WjmaSEh8Ev2XOea938LyiXw9anB4BGSOvJrKTTLXY2qKKKkYUUUUAFFFFABRRRQAUUUUAZWt3sFjpM81yR5fllcMfvZHTqK+a9VuzqepSyAcZ3Y7Ko6CvVPE5uvFt/PpGk373iI/mSm3yY1RkUxru+4G4c5zjHfcQp4rVpvAvgycwXtzLrGpwqUaysuI1kwcrLLkZ+bjK4YY5U9K7MPUjRV3uzmqwlUduhiaNpd7ftLcxQSNDCA0j/dC56cnuTwB1J6ZpmpXEIkeYH93Eu5t3PPpXdaZ4ouNY+Gl7cyG102X7VFFZQWvyLkMspCn5vnYK3zE5z2HfxXVtUMqtaoQYw3JH8WK6FiZNOT+Rm6KuoobbyC81Izz/wCqU72H8hSySS6nflycs7YA9P8A9Qqq5MECxZ+c/M/1qusrocqxU+orOGmr3NHrtsatzLHG5RD8ka7R71UUZJkf7x6Cqy/M/PNW1GMMetNsEhHhcADjnkiiNHTPpT8sTSbPU1LZVi7p2q3mk3yXdpJslX2yCPQiu/1/4ka7Y6Bay6dY2ht5oxi/hByG7h1/hb615psA61NBqN5Yq621y0auPnTqrfVTxWEr30ZelrMl8O2+o+JfFsM9zM7tJL5s1xJ0CjkkntxVvW7uC98UX11DxbeaRHx95VG0H8cZ/GqseoajLayQLO0dvId0gTCK31x1pIreNcEjdju4wv4LThBrVik07AyNfSDYhKj34/OtK10dmXLK0nfavyr+JqBLxYR+7RXb++4/kvSori/nuDh5Xb2zgD8K00RJsfJaoVNzb2w/uQDex/L/ABrIuZmlkIMjbB03dTUIjkYYK4B9eKmighQfNvdvSMf1pXCxX+Y9Bipo4yOTuP0q0kEjf6q3Ye5NRy+dbfeeFfbeM0XGWYbkRAbbRSfU1Z/tS7Ix+7j+rYrn5dS2/fnX6bs/yqsdVg7yufoKTa6sNTqheXR/5fIc+gc1Ml7KhCzTx8+slcYdUgzw8n5VLHqMMvDXLD/epXj3CzO2E0Ugz5kcn0cU03NhDJtkRdx9UyP0rloCh+aOf8Qa0IZVPEhjlH+0AT/SqA2tlrcH9y/l+wNWjZXRtvlljuU/55zpkH8a5+SwuZcvaSrt/wCeZYj+f+NQJqGo6dJtZpIj6HoaevQWhoTW9k+YprR7NujbfmQ/8BPH61n3Hh+W3Rri2Ili/wCekLcge4/x4961oPESSx/vIx5479m+oqaLUrJ2VvIezuM5EkRyD9RRa4rtHMLcPbFfOA2N92QfdP1/umriiGYcov0NbV7b21+jPtRJm+88Y+ST/eXsfcVzMltNp8xWMMyL1jzyv09R7U9Y+gtGXxDCBgIv5U7an90flTIZkmjDocqalFUnclox5FC3DrjHzGlKKT0ps7E3Eh6fMaaGPemwjsKYlPSo3h9KkyTRkii5RSkDICcdOalbImY4qS4GYW+lIw+Y04LUTE3ewo3ewpcUYrQkM0cGjFGKdxBtXpRsHpRikxTuAuz2pQpHc03n3oyadwIyP3mKWRdppD/rKWUk4piHou5c07Z702NsLT9/tQA3ywaXYKXcB2pd/sKAE2e9Jsp2/wBqXePSmA0J9aXbxilDCjetAhAnOaUpuOTS7hSbwelO4Ao2ggHrSN1yTTt4x2qMlnPtSbBIjYM5wKfHCq89TUipgU/FJR6sdxu2kkXMTDHbNPApcCqtpYkrqcimtw6n8KBxkemRTW6fSsHsaLclVqVe9MXIPsaeD831GaZJLN8xR/7y/rUR45q2V36YHHWOXafow4/9BNVDVR2sNnQ28Xg1Yh9p1XVHZlxIqWaqvvjLGlkn8DR2yx+frk6IwZWVY1OenUj8K55VUsOAaYtupiu4e6Ftv86hxn/N+X+Q1KPVHRHUfBcdwrJY628u3qbmNd31+So/7a8IJFKsfhzUHj53K9/x+iVz0gUxW9wB/FhvxFOSNReyxEfLIoYVPLJ/a/p/Iq8exvt4i8OhYQvhUsAf3Zk1CQ7fyxS/8JVpn2iR4/CNj5hGW33E7b/r8/euaGDp+cfPE4OfoamciO5glxw6bT74oUW9XJ9A5l0Rt/8ACX2yWo8vwnowj3DhllYKfxelPjOYTIi+HtDUhflb7HuP6k1hiMhb2DGdpYr/AOhUkh3QWs45AYoT9RkUcj7v736BddjZ/wCE31NYpDFpeiRMDhwumw/rlTSt4815WiCDT40bO3Zp8A/L5KxSjG9ni24Ey5X3yKiEcr2akIxaF8sMcgdDR7Pzf/DD5jcPj3xWxkC6gEdP+edvEv8AJaYfHvi4xpKNdugCRnY+3+VZhjdLlJ8ERTKBvxxu9M02OyuXElj5T+f1SM9W7jFJ0l18wUmag8aeKxc7H12/bjcoa4cj+dUpfE3iKaFpn1vUCwb5h9qf1+tRC2leWBiNrx5V1I5X61r2fh8ohluXW3ikO7951b6Dv/nms5RihqTM0XOs3Mq51C7ZHUkEzMc1p2Hh/UbpBJLLI8ef9bM+1Pzzz+f4VoJc2FiMWtuJZP8AnpKN36dPzz9aimvbu9k/eyMx7KvJqWk3sO5YFno9mf37tfTL/BEAiD8T/QCpzrl1GhSyjisoyOfIXDn6sfmNV4NKunXe+2BPWQ81aEOmWvMha5kHrwtGiDUzVM1w/wAiSzuepHNWBpd6Rl9sQ9Cautq+AEj2xL2VBzT9zld7gL7yHFFwM4aTzhpgf91c1ai0uJBl+fd2xTzOGOE8yU/9M/lH51SuIXnbaZET/YhUytRdgXDPp1tx50bMO0a7qjfXYlB2RnHrI2P0qiNEmb7lqFH9+5l5/IU8+Ht4zNfRKf7sUfH60WQCSeIMfxo3svH9KqS6/O/3Pl+lR3mmW1qPluyzemKzRtJwCDVaAWn1K7k6zOfxpEvLlOksgz71VeSGIZkmQH0Byf0qrLqSLxEhb3PApOUUFmzYa8mcYf5v97mnJdY6wxn3xXNPeXMn/LQr9OKZ5kx6zMf+BVPtl2H7M7W1u42cB4gPpmuitVtpVBWTn3ORXlCzXCHIkfPs1XINb1G2bKXB+jAGj2wvZs9ft7IseMOn5iuh01ZIAqjcyDsxyB9DXjdh491K2YebHDKv02mux0r4laZMMXgkt3913A/iKTqXDkserqLiOHzljaSFeWKfeWoZbHStWhmluLaG/imB3b8Ebv7x9x68fWszw5430qeVUstSt5G/55s2M/ga0PEXg2x8R2cuoaK72OqBdxWJigkPoQP51PN0Y0r7HDWenQ2evDSkLoyOXCSDnb16969z0q2Wz0u2gUEbUBIPUE8n9TXy3Jq+oWl49hq8k3mwPhJXb99bt2wT1HtXsnw++JNtq8Mek6pKiahGNqSjhJlHf2PrWc4djS+up6fRRRWZQUUUUAFFFFABRRRQAlYvibW/+Ec8O3erfZ/tH2cKfK37d2WC9cHHX0rbrhfiNJdT6D9ktFRmKvcTRyIzK8UeAV+XnO94zx/dPPHLiruwm7I8Z0i71HQtM1mzZ7uyuL+wa6iI8sL5aeYhZt4ypzuAKnJzxzivLPvzcdBXpnizxBNpOn32j2F5uuruZra+cRqyS26KvlBQclMFn9+5NeZhfL+taSd5NkpWVj1ZXfTvgdClwrt9uu3mtUWIDYFO15GOeR0XOOCRzg15laxtM8k+MpEN7fngV6d8PvGtnpGgnT9QluxOsjm1ELk8PsO3HAA3IRndnEhG05yOO8W6rPe+IL37RcNNslZB+9Mi8HHykgHb6cdK1gm0r7ESdnoc/JIXYmm5odw5yBikUZYCtbk2LdvHxuPNWQmOtCLsUCnjJGaVx2ExSMyqMscVLBBPeyGO1jMhA+dugUepParQtLWzO53S6mHVjxEp/wDZqW+w9ihHDPOu9EKxf324H51ItvFH/D5jf3m4X8BU02oBmySXb+8w4H0Wq73TOeBz/fbr+AoskLcs5RRudvpu6D6CoZLxC3yAt7moTGZCMb2PqaeY44E3zSKg9ByTSbCwm9mOTUqK4wcrHn+Jv6VT/tLewis4cMf43+Y/gO1a9nZiA+bMfNl6/Nzio5r7FWtuTwWgI3P5knuflH50261W3sRsDJvHSOBMn8TVa+1dIyUQ73HYdBWLumupD5Scn7xUYFTKY1Enu9cv7kYUCFPrk1lssj/NJIzH3Oa1I9OSMb7mQAegNMkvbK3JEMAZv7zc1m33KM9baSTiOJm+gqVbF1XMgVP99sUyXUbmbgNsX0Xiq5DsfmYk+9TcotmCFfvTQj86aYrb/nun61AIvaneU3pRcCaNERt0VyA3s2KuR30wADbXx1OKzTEfak8th2x9Kam0KyOgXWZ7U99v8JRuRUj+K5biEw3dskydmB2tXOB5FHqPQ0oZG/2T+lV7Ri5UbCX9s7AAvH6b/wDGtG3uyvdZF7g81zDKRjP506ORo23I2DWsar6kuB32n3Mcr4UmMnsTwa6FdM+1RlHQZxwxGK84stUQMu5tj569q9J8Oa7DLEkczKW9Sa059Loz5O5j6r4Tu7MPd2aF88yRj/lp9PRqwknVlUg5B6Hp07f/AFq9402a1aMLNGssDDDL61wPi/wOX8VPHoeZftMBujBjBlABO9PVuCpH09ahT1G4ux5tcf69/rmohuqaYfNz19R396YBxW5ERA1OwDSHAoxmkUMmH7l/pTgmQCTxgUkn+rcf7JqWIZiQ/wCyP5VUSWM2KPegp7GpsUVoKxXCGnbD3qam4OeaAsRlCKaQfSp8U0jNArEOKTFTFF9MU0qKBEOwZzQUBqQrSYqgGBNtLS4NGKLgJRS4+tGKLgFFFFO4gpc8YxSUUwFLIRijCY4pu3mlC1OoxfK3HrS7dnSgEgUuSapIQcmjkU5Wx2pxcHtVCG5NJuxTsj0puRTEQsP37AdDzQ0fymiXiRT6ijcawe7RaBOcCnE4IPpxUYyDmnZyKSY2aFn+9tb2IdfK8wfVWB/luqn3q5ouDq0ETnCTEwnPo4K/1qoVZCVbhhwaqO7QnsaOl2ujTxyPqmsSWTKcJGloZiw9c7gBWosXg1GNyNa1FpUHzbbFR5n/AAEvXMbQTyM0bR/dFDU29H+CBcttUdGLzwREJY1TXZIX/wCWflwqF5yCpySMGon1Twh5aINK1uRo87HN1ChAPY4T8awdo9KjYg8KKXJP+b8v8h80ex0Z8SeGlunmTwzevJID5gfUQFfPByBH3qI+JNCSEwp4QRo924CXUZGwfbAGK5/AUcCmnntR7N92HOux0LeL7ISJInhHTRIgwrvcTsfx+cZ/Gk/4TMoZPK8L6Ggk4YGOZg31BkxXPGkpezf8z+8OZdkb58bXexUXQ9ARVJ2j7Du2/TcxoPjvWjIXS10aNzwWXS4c+nUrWEkTOcCrEMIdtsY8x+5B4X6t/hWcuVdW36stXfQ2I/GfiZwVS4s4U+8wj063XHv9z+daX9s+INSsDHqGsNFYSDDMyLGHHooRQzfhge9YkZit8bUSaZf4mX5E/wB1fX3NSLHcXsxZi7yHqScmstWVsXFvbOyUJp9sS4/5bzgFv+Ar91f1PvUANxeS/wDLSR269z+NW4tNhhG65kA/2Fp7alHCvlWsePZByaLiHw6UkQ3Xcu3/AGEPP51I2o21mu22jVfc9apmG7n+eeQQRn1PJpC1pYjITc/96T/CkMe099enKghf7zdKhkFpb8zzNK/91KqXGqPP8u9iPRflFV1gklOcYHt/jTAuDVyjbLS3jh9wNzVYhkuJf9a4Gf73zN+VVAlvZpvmlSNfryaqyeKYrb5bG1DH+/If6VLmkNRbOqgtGYcxs3/XVuP++RUzz2tmn+k30UI/urha86utf1O7yJLyQKf4Y/lX9KzyzEknk+pNQ5spQPQ5vFGhQtjfPOR3AOKzbvxtDtK2emoCf4pjn9K43JNAqeZlcqLVxfXF3IWmkwCeijAoM6quI1X/AHiKqF1UepphZ39h6VLkOxM8qk/M2TUZmGflUfjTRHThF7VN2Mb5z9sCk85/WpRH7UeWPSjUCMTPSic9xTjGPSmmL3ouA4TKT6VMCp5HNVDGRTQSp44pqQGmhKEMDj3BrodM8aa/o+02ep3KBe2/cPyNcilwR96rKvvXiqTTJaOl8Q+J7jxLcJdXiQ/aFXaZIowhb6461Q066e3uUlhkeOVHDRuhwVI6EVlK+D6VPG5jbeje9VcD6q+HPjlfF2km2vZY11q1GLiNfl8xe0qj0PQ46H0yK7yvjvw54hvNE1m11exYC4tmztYZDqeGU/UE/wBK+t9O1G11bT4b6xmE1tOu6OUdGHrWclYaZeoooqRhRRRQAUUUUAJXj3xCu1uvEf2ItdukLQ2yRKf9ZI7ea4XHX5TEPbivXZZEhjLucKOpxXiHiu9kudfgmhdBeWt5dXG+aHah2HagDHCt8iRn6KTVQ3uRLseb+L9D/sjQtCmupSdSv4nu50PZWb5PxwvNcjp1jPqmq29jbKGmuJVijDEAbicDJPQe9em/ErRZ7TUby1mkjE8bRx2sSxKPMhCbsqc5HLMOOpUiuU8H6JLd6pqkpAibTdOubx/MTcBsQ8EfU49qfQZi3Nvc2GrXVncMqvaStG4Rgw3KccMOtU55GlkZ2OWY7s1LFEdgjH3pDk1FchRcOifdU7a6IrljqZN3ehEKsWy7pQew5qAKaswuFIjDopbq79FFOUkhpFxpFTGeSTgAVrwaKUUTaq7QJ1W2T/Wt9f7o+v5Vkf2xFpwK6Wubjo17Kvz/APAF6IPfr9OlRaZNdXbtCzMyMxeSQ/zJqFJNlOLsbV7qieT9mtkWKBekUfC/Un+I+5rJaR5TzzU1y1rb/wAf4nqaqwyyXLfJmOL1HU1bl0JSJREA2G+9/dFWBCFG5tsa+rVXkvbezXbGuX9Bz+tZUtzc30m35mJ6KtQ529RqJo3GqRx5S3Ut/tniqUNvc6jNkc+rHoKmi0vyo/OvZPKT+7/EastqaRRLDZJsHqR0/wDr1D1+Ia8i5BFa6Ug3ODI3c9T9Kp3F9PeOY4VKpnoOp+tQxRtO7AcseWdupqZ7uGzHlQr5kntScuw0tR8VjFCnmXLg/jgCkl1GOOLECgKP4iMD8BVGWR3Hm3L59F7CqMkjTv7dh6Vm2VYknu5J3JyTnv3qNYS3vU8MGQcfnVuOJUFIZVjtiRVhbdcZIqU8dBxSMxPfHsKAGGNRRtUU5cHk8UNsA96AGbFPel8oGgU9RimBA0NRNBVr8cUhOfvD8aAKQLx+mPTtTgBIPl69wastGD0qCSIj5hwfai9gG44z1x1qza3U1tIHgkKkdqrq2488N/OlHBxVpiZ3mkfEa+syqT28cq9ypKmvVfh94l07xT4jtvLjmNzaRySJ5y58tWG1trehyPyFfOSkj+Ve2/CyNfDnhi61+VP9M1ImC0X/AKZqfmb6Zz/3yPWqezEjlfiB4ebQteuGQfuZJX7fdO4nH65/OuV7DmvWPGNp/aulSbh8/DqT/eHT+o/GvI19O4rWnO6MXGzH4B60HjFGPWlwPatQGyYMbD2ohb9zH/uilfGw/SoouIYv9wVUdwZY3Yo3VHmkyasgl3UpaocmjNAEuaTNR59KM0wY4mkzSUUCFpKKKACjvSikoATFGKWgUAJj2pMU+koAbijFP60YqkxDKXFO460U7iG0dqdto20wEpRQBjrS1SEJijHHalxRQIimX7p96bipJR+7/EfzqMVjPctbB7cGlBIGBwPSjFGKQx0btHIroSGU7h9av6qoGqXLIMJI/mr9GG4f+hVn4q9dt5kdrJ3MCqT7qSv8lFOL99A/hKmKXFFI29+AMD1rczbI2JY4FJjaKtxWk06nyYnlx18tS38qqSKVYqwIYcEHtTasJMYTTT0oJyaTgDJPFZzkoq7LSbegmM0q4DbcFmPQDrQoeU4XhR3NWoQsPCdT371ySquW2iNowS3HxWgxm6Ygf88oz1+pq4m+UCKCMRxj+FP6mo44s/NIdo9O5q0s77dkEeB6moGSx2kNuu64f8AaeNQYjyrOIKPUVWMSKd9zLk/3RTW1DyhtgVUHr1NAFs2rsN95NtHpmmNf29qu23UD3xyazHlmmO5mP1NNPlRDe5/FjiiwFh765nY7Mgnv3qL7NzumkwffrVKbWEQFYhu+nyis6S/uJur7R6CpdRIpRbNuW9s7P3b0rOuNauJeIv3a1md8559acFrNzbLUUhHZnbc53H1NIMGpREAMuaaSOwqChOlJmkJzRj1oAM5prPnhaUnPApyR+1S2AxUzUojp4TFPAyOKQDAlLtHtS4NOCUAJgeo/KjaKf5dJtp3AbtBppSpdmaTBBx1pAQlKiaIHpVsgdKYVpgUWTbSo7IeDVllz1FV3jK80gJ0kEgx3qZTgDFZ6sVORVuOQHn86uLFYv20/kyHI+U17j8EPEix3V14cuZ2xN/pFkmBtBAPmKD1zjacdPlb8fCMZFb/hzWbnR9TstTtXIuLOVXHJAYd1OOxGQfY1TVyT7LoqpZXUF9ZwXlu++GeNZI3wRuUjIPPsat1kWFFFFACGlqGSUIO2PenxtvjDcc+lK4EVwiSW0iSNiMr8xzj5e/6Vymum1bXLPT78x/2dIvmIjtgCSJhKflxjbsTHHqwPU102oCRtPmWJ9j7DtbdtwfrkYrzSey1K60W7ktYUllSJpopIds0kc0cUhjDL8zHP3NrBuG2gCmmJq5p+JdN8O+I5Ib1hPdRWobetpGVGMqC7ScNwq7flOcN0IrzX4qf2Bo1va2/hi5RTqkZF4sMgceQhXapz8wy49f4TmvTdNtdVs4I9Q8Pwrc6bfwpPGksgyFYZGd2Ox/xrm/Etp4e1zfDqfh4WuoqxV2gDb1P/AAHG4VpDlvZkzUlqjwyyVYo5L6T7qfdHvWSweSY4Qs7noBmvSLzwWblfs+mNJNbRfMzmKSMJ7uzKAMfWuR1W707S4TZaVN9ouDxNeKNqgf3Y+5HufwronJGUVqYt5dyyCOJ0VTEu0YXB/GqbMzYBOaTljV2GCOFBLc/VUB5Nc/xG2wtlYed+8mJSEfmas3OppFF9ntVCoPTp/wDXqlcXklx8v3Yx0UUsSRwYkuFJzysY70+ZLYLX3JIYDKPtFy5WL1Pf6UlxqBZfLtwY4v1NQySzXkoABJ6Kq9q1IrODS4xNdgPOfux+lF2Fipa6S86GWdxDCP4mqxNeJZQiKyTYG/5aH7zVHcalLOQXRSB91Ow9/eq8aMzF2+dyepFK6S0C19xp8+4kDTOzcdSal+RPlVadIwjTH8R4qJizkIoG5u/YUrjHyXTBBbwDBP3j60RxLCpY8nuTTooBCD0Y92qvdzfwD8aljtYhnlM0nHTsKkhhzjio4UJ5rQjUKopAKiBRUoBK8Uiru7cU4nHyjgUANbA+WmBWZgACWJwAO9XdP0y51a5W3toy2TgnGcV6BYaNp2gLLGVFzqUcLTvEjDeEHVif4R7D9aAscXYeFNVviNsPl55/eZz/AN8jJ/OtyL4eyLj7XfxwsfUqv/sxP6VbuvFyW01sJxmzmPzQ2jbQoBw+T1z0IqvAb1NbYPYxn7L5jRTkcHCMQRzlg3B/Ki4yI+B7MnCa7a593FMbwDeMpNpfW1x/uPn+R/pVQQ6mkNtbxTJHOzkmTOccYAH4H9K2L+PWl1K2KRQSxeVBG6qSDkRqC2e3rS1A5LUdE1LS2K3dswUfxAZH+frWd9K79fE0li4t5ZPP0+GJRI1yPM3N0Jz1BY9MHgfSpbvwxpXiK1F1pDpb3EmSse7dHIR97afbIzTEedChhkVZvtPudOu3truIxTJ1B/pVftQBVkj7jgigNuBI4datFQ1VmXy5N1MDe8IeHpfE2spbb/ItI/3l3cnpDGOp+p6Aetet3k4nurdLNBb2MEa29rD/AM84wML+J7/WsqysV0/wpaDRXjks3C3EroMNcN3Z/pyMfw4qWKR7iGXrlcEH2/hP51pzJ6IVmtzRllefT2iYEttP6V5XqtuLbVJQBhXbNeowTiSTkcuu/wDo1cH4utzHfkY2nPH8xVQ0Ikc/njFKCKYD8ue1Lu9q6DMG6EU2Jc28X+7Sk+tNt3BiQA8gVUdxMftIpNtSE55pMVYiPBFJ3qQj86TGeaYDcUEUuKTBoAPwpaDmgGmID1oo9u9OU0AJjijHFL2pRzQIaPTmlAp2KQ9OTQAgHal20uaBigBNtLt4opc8UANxQBThRTQhuKMU7p1o4qkA3rS7aUClAp3EMxijFOxzS4p3EQy/6tvwpu3rUkw/cP8ASmmsqm5cdhuKCKXHNKTUXHYYePepfN3QRqeiFh/X/Gq8sgQ4HLU1GyhBPcH+lF7WfmC6omMuenArTXxJaafGi2eg6eZQOZbvdcMT9GO0f981iySBchetRLH3bkmtZ3loiI+7qzp1+Ifiwp5cOryWcXaOzRYgPwArBnnkuZ3nmdpJZGLO7HJYk9TUPCjPQVGZHdsRg/WsOeNP4dzRRct9iRpAvGct6UqQM53yce1Pt7fYA0n3/TvVxIt+OOPSsW3J3ZorJWRCibhtUYFWobfGAq8+pqxHFDEuZHA9AOtJJeAcRIB7nk0xXHeQicyHJ96Y92F4jGfeqryMzfMcmmOVRd8jgL707WWoDmd5G5alVFXnH4mqZ1GNATs/3R3P+FZ9xezXBwx2r/dWpdSKKUWy/c6nHHlY/wB43r2FZUkskz75HJP1puDjpgUYArGUmzRRSDFJ16UuCTTwMe7VIxAnPv6U8sEGByaQtsHHJ71EW5oEKzE9abnNJyaXpx3oGHfilPp3pQNoyetCgk+9S2AInapwABSqtKPakAAUoPPAq9pmkXer3HlW0eR/E5+6v1ruLPw/pOg232m6xcTKD87kBQfQZ4z+tAXOMsdC1PUMNa2chQ9HYbVP4mttPAWo7VeeeCMHuGzj+Vblx4imlgtjZIyhp2imVFA24AIG70OfaobW91rVb0wXy28VvNE0EYCqAjH7rYA67scn3p26C82Zo8DsxAGpQs3oAM/zqOXwJfgEwzxSgfhU1rBeLaXTOsXnxRmM7l4LFsD8ev5UxLm/0yNkS2/d4wZEGSfelZlXRh3eh6jYZ861kwO6/MKzTwD616XPripqstorh4l2piZerEDgY56+tRX+haZq8zQRmO31ADJRTnP+ND0Dc852g00jHetDU9JutKuDHcIQM/K46NVLAYmgRCy5qN0qdhtNMYcUwKLptNCPtPtVlkBXmqhGDikBoxNmrdq+yYjsazIH+X6VdjbDqa1TuiT6t+FOpG+8A2sbvI8lm72zNJzwDuXHsEZR+Fd3Xz58N/iBbeGLOXTr60u54bgrNEbZFO1sbW3bmHHyr+Ve36dqg1F7uMWlzBJay+S6zoBk4BypBIIwR3rNoa7GpRRRSGU5I2lbaOlWIohFGEFPAAHFLSSAZkAZ6CvPdc8V3uhWAuobWGK0tV8+aBFA81N5B2cfLnPXnnHTnPfyOkaFnYKijJJOABXlfi3xrZNb3ei2Oh29xa3aeU888wt45Cf7oALP9eKLpNNkSbto9Th9N8Wa1e+K7CKG5EuhbYtGtpIBJHChkGFOw7B5u1ipYLgckDAFek+EZDH4Ukm1i6trt7eyiklmnmHmscuxeR2+ZV3DywzNj90zDArg9M0+HR/DgkvVV7bT5JJ/MHzZmk2qFTP3m4C596888STDUFtxcznzogVVF52JuZvLU+gLsSx9fatnD3bi5vesWvF/xFv/ABCRZJdznT4z0Y4Mv1Hp9ea4Uq0kmFT7x4Aqw0kMC7IQHk7yHt7L/jUaTGEMRzIR1x0qSkWBHHp/zS7ZJ8fKg5Ce5qttmvJS3LseWPpTrS2e6m5+4vLt6Crr7zCUT/RrPP4vT3AqHyoMKgEs3r1A+lOktZFG+ZvnP8I5P4/4UvmRQcQphj/Eev8A9amztcoxhZGjbqytwfxpDJ4Lp7YhYwvmAcY/hqNy8hy772z1NNijEY68mnGRV4xk0rjBIv4npWnA+WMZNJsdzmRsD0p4CpwooAi8p2bfKfwqdSM8cUwktTgMCkAO21c1mnMsufWrN1JhAvc1BAuSTSAuW8Y59BU+MnFIi4UCpY0Oc0AKcxrjg5qfTdPn1K8S3hUkt1PpVdvmfmvQ/C1kdG0GbVWgL3BGIo+7Meg/X9TQBeRLPwzFHpsDCO6eNmmuBj92o64z1NYlpqUkPiGzjigaawnVlF2jEvPG42ytu9Ap5Xtx0qnrxCj5obqW1viTNKY/3kcmOVPoV7eoz68XfDlqdHheJmFxGzBim7b9GXPAP40WY09dRx8PPpt4Yp1SbypNqShONwG08fwk7a6RVWayinOC6jyX/wDZf0yP+A1HrDiGSzv45jl0VJDj04w3bsDj3qCz1SznuXtLfaJZf3e1Cdm8n5Pp8w+mCaLaivoULi3xcSIucK+5K1L2by4440XEsyLk/wB1Nqg/n0/OsSGXV5neRrSOC08475XceYuPvfL19uaS+1C4g1ad47CSaI/eCNuKEKvA9cAjpT5WlqhXuXbTS0liEUkKPnjHqTUdxpk9rd27aVJJ5EIKfZo8YfksW9stznsPpV/TblGgkmLOoDGJcr1YD5seuB+RIqO7vZXVkiQwW6j5lzlnPv6/54pJW3G/IJobDxTZrp93dwy6inyxXMQPzNz8oJALDjG7ABwa84vdOuNMv5rO6j2TRMQw7fUV209lqCfZ7jTpIlm3q1wsm1UK+rOeQoz60niiK38S6KdYsysl1Z4SYxjAlTs49s5p3uhWscCfl4FQSqCM1MSCtMYUhne/DDXCRPoUz8gGa1z6/wAa/wBfwNdbeW/kt5sOEHTGOB7fSvF7C+m0nVLe/tziSCQOPfHUfj0r3bfDe28dzBzBcRiRP91hmp2ehe6MOGfYrSOAnlzbSPQMP5VyXiS8e61I7tp2KuMDrxXcNYuGIaMOn8ORXM+KdLWCRbsgBnULtHbFbQlcymjj+jFfQmk3AmnyYMzj/PSmcY4x+FdUdjIa54NaF9J5tnbPtQYO0lEC5wMDpWecjpVmSYtaIjHO47hg9OTWlOaSaZE4ttNEQzS9CelMOQM0oO5aaGPHXikOeKMn8aAcYzTELgEcnmmD5TzTgMnrSEZJHamAhbNIBmlx0xS9OO9AhMUgpx4yKbzmgYoxSikHXNFMQufegjikwDQTigQoHA70Zxxikpcbs0AAPtS/XNJig9aAHZozg0gx60meue1ADifyozTQaXOe1UhDgadmmDnpSk0wHYooHIFGaYiOb/USf7pppHFPm/1D/wC7Ufas6m5UdhfxqCWbZlV+9/Kkmn25RPvd6qk/jUIGIzYojfL4bIVhg4pp5oVdzDb0BqJ/Cy4blhQudw/AmlZ1Tr1PaoTLtwifMw4zUkNuXbfMMjsT1qZ1nLSI4wS1YxUedjnp6dhV6KMJwi8njPr9BUsVuWT5QFQdzV6BTHxbxkuf+WjdT9KhIpsiSy8td07bP9nvSNOiZCcCnzwOjYmb5upGcmq4jBbnpVJCuKvmTHC8D+dOeHZwTzRNeJbRjewQdgOprEu9SkuMoo2Ie2eTSlNRGotlyfUYYPlj/ev7dBWXPcS3L7pG6dAOgqIdKQ/pWDm5bmqikSRp5hI6mnvCsKjc2XPb0pVnWNRsRQcdRUDOztknJqRgWzSque/HrQopxOPvH8BQIBgD0X+dNMmOF4FNZtxyfypNpNACE0lSCP1p2EHbNIZGDxTlT+I07cPSgnigBCdxqVF71Gi5qwqj6GpAK0tF0iXWL1IEysY5d/7oqisTSSLGg3MxAAr0ezsI9G0YWqzwwTyrl5Zn2KzY+7uxgfjTDyG3c6aLp1tDp6KlrM7Q/aB825x1XPb8fwqHTLaa4tnj1cia3kcN9nQAeWw6Mvv/ADqTS7e6soHTVIHWzusF4kHC4+7IvbePbqCRVuSFrG4MLujKQHikX7sqHowp26iv0GXOn/ZbWREAKDE0TAYDY+Un8mqoJCYfvbXHcfzrTj1KO3k8u5ZTby8Nk8qTxuHvzWNf201reKrIfs5yVlP3WUdSPTnjBptX1QeRs3iq8C3I4+2uJGHoyr8w/wC+jUBRQo4xmlCzSaHEzW+2SMfaFO7IILFWH5BTUOnSpez/AOt2pGy+YzrgjnAUA9yabWok9Bbu1SG5kugQlxIz+QcZP90vj26D3+lYkV9c6VcLB9jWSF25Qcu5J+8G/ve1azyy3V5LcyDG47VLEKAB0AzUkNo7p9pT95Kp226xqWIkx94f7o5+uKVrseyLkrWWrK2m3DrK235Zcj73cfX+eK891fSZtJvWhccfwt6iuos7GOylFq0NzdSSkhY7Zd+yTOdzyfdz3wufqK0tVszrmjOXi2XcB2kEgnI+nrUNWZSd1Y80PPWmEdRUzoUkKNwRwR71Gw4piISKqzrzuFXCKhkUFDSArxNtf61oRHgA+tZg4NaVqDJMgAJ9quImepeDfCr+KLS7hjiZpY7YbWEuwj5j0PT8x+XWvYPhzpl7o2kXlhqd3Nc3TXJm3ShtypsRVDE9/l9e1eYeFvFkPw6+znUYN/2qE+cgOHQbvlwK9e0nxDofjDTzcaRfxucguhUF07fMh9QcZ79OelVPT3WZxvudXRWPd6j9ghM0sNxsMmCpAYjPcEHpweOvI6CtNJA6K6HIYZB9qyt1NLjty7tuRuxnHes3Wda0/QNOkv8AU7lYIIxnJ6sfQDqT7CsXxh400/wrF86rNftHlI+mF9WPpntXzn4l8Sa34x1tZLiV5pGO2GJBhUHoo7fX86G0tWHodF44+LWqeI7hrHRxJZ6eWwox+9m9C3p/u1Y8JeFharJqurzESqMyzP8AMYwf4V/2j69qpaJ4atNE23V3Kr3gH3xysWf7o/iY9qj1vxTK7iCPEUMPEUStuEZ7s3Zn/QfWrg4/EyXpotyX4qeI0gvLHR7NRHb20KzGMcfMw+XP0Xn/AIFXlVxdPKxO47j95vWuq+JaOPGE855S4ghliYdCpjUfzBH4Gue0nR5tTlJUbYVPzO3Srm3KRMI2WpXgtiYmnkOyMdCe5p1rZS6hM3kqFRfvOewq5etarcFHlM6Q/KkaLhaqXF/cTKUBEUXTy4+F/wDr1GiLRszXVnpdr5EO2RjyQDncfUmsG4uZro+bK3HQD0/CmRwFxuc4X1NTKUXhVz703K4KNiKKFydx+Uepqwz8nksx6k85pPmfrTlRV+tQUNCs/sKkVFXtk+tKGyOlABoAD160A5o2/jSrigBKDRnFIySMj+UjOVUs20ZwB1P0oAz7h98px0FT2yZUe5qqQetaFsvyoKQFsCpQNvA575qNRkmpDwPwoAks7Zrm8hhC53uB+Fel6ysMbWenOhZLO3N1IuRtJ6c+v/6q4rwjAJ/EdqpB4bP8q6vxAz3GpamscsFyV2R/ZC37xeOdq9TkH+E0Wuxt2RzvhzzJtbuLiHUEntLjIng3NGxx068Ag4wQf6128mnvGqsr71+8pdR8/sfQ/wCelczomlRWT+Zbq8YlXOHbci88jcQrA+zL2610dtOIVWQyZibjMYOM+zdKYuhXmuylrNbW6CWVtrNAMqWTcFb7vQjcpz221Z8M6Kl+s9zbTtFGcNwqx3GOcxsy+n8Lc5wen8OdNNJHrZeS2jkjjiLJeBSWlV/kYDbgAgE8EHBH41s6Docqtp99aPNa3B34tmZpnk/h3/L/AA8dGxz2Fa01r3M5PQ7u08OaZLdpNBYWJhZn80zR7hLxu3nPB5/rWRLoelX1xPOlnHagsVE0GVZx3yoOG7ce1Zsuh3kdvNFNfaolu8q+YGDqYVG7AUtg7TnHGcYFVtUvhaXQhS4uJr1kzneSyJ0AOPXHX2q/aKLs1cnkb2Zg+KNMuLO5s5PtUzSRxMYrhNrRyDdllK7sKeny9sCq1jHeajJl7eWCJWLO0kTc9h9T7CrkvkNZGddkMUZLZjgTzHYf3dwPOB949P0rLfVJrzVl/wBJJsWhX7NASSIz1bk+/wDEeTWU7bs0j2Rq3scssD2q7IIWGCJSu5z6sAc/hjiqGg/2VYaumnw36MjxeRPaNEVJDkDduJ+b5jkY6CtCGKNFDFcHGCfauc1KHX59RY2GlwBGH+sEaSYVe5cj5fzrO99i7WZzOs6edN1m8smH+pkKj6VQrs/iNbhNdgvlGBdwLIfrgVxpFAvIgkHFetfDi+/tDwqbWRsyWUpRfXYfmH/s35V5Q612nwuujHqmoWecCWESAe6tj+TUmVE9MLhRtPUVxvjab93DzwM11r8nJ61wfjiU+ZGh9OP0qqe5M9jjncvIx6Zx/Kn/AMPJqNBtLc96XO786647GLFZSQpzjFMhICYz/E386lKtt5J9sVFCcBvZzVRWpLJivr0pvPalzk80pB2jb3rVCEJ7igfexSBcdafj1HPvQAYJ5LZNIGJ5owM8A0EDHQ4piDJB4NG7IPHNJ24NA4NMBcHaefwpuDj1p5PNJk44FAhoyOtHXFKcgeopM560AO5ByBRzSBjR15piFzgYpOhoOKN3yigBw4FN70oOaQtmgBTmlAoz3ooEGMc0vam/hTs5qkAdKXNJ27ZpQcUwFB9adimg4pc55qkSMnOIyPUgfrVaabapA+9/KpJpCxUdhzVOT71ZSWpSehGTTDk1KqM7qiKWZjhQBkk0BAgLycAHGKzk1FalRVxqpkZbhRSFmlOyIYXpnuacFe6bJ+WJatptUbIl4/vdzWDbkapJDILTa2CMt6VoxQIWH/LR+wHSmWtrJMTj5UH3mPSteCMQR/uRsH8UrdT9KLWFcRbMJhrlwvon/wBanS3BiQrCvlD+83LH8O1MecICIRhieXPJNULm5itV3ytlz0Xuafmw9BXOBvkfCn+JzVG51JFG2A7n/vnoKz7i5ku5d8nA/hUdqrO+B71lKq9omkYdWLLIzsSSWY9SajIx2zQDgZPU1G59KyLAvz1pASaQDn3qQKSOlMQYA45pyjd1OBShQOtLn0FIYrYK4UfjUewZ5andaMUXABsFG7FGKMUAJk96KOopQKADFBGT9KU/KM+tOABOaQDo1qULxk0iDipCOKQG/wCELFbnVDcSDMUC7ufWtbV47m7vI1vhJAA/mxxPwJE9vXtyKXw1bmPw3cyIrM8zFAE6kcD/ABq3pYvo5ZIG051t124jnV2XnkkBvun3GKaQi9bXz28YjhcRoeGQEYb6qeKlXU7SaJNPu4YoQz5hnicfIx6jYT0PoCKlOnJJzbKIJD1SVcofo3b8fzrLurS/uL6KLbHHAsZZt5jXJGMDNUrrYGSweG7u5u1gtpra9vjKB5ednkr6sp5A6c816FpXhCwuPt9nqh+1S7hI0TkiEMBnKqOee/PPFYnhma50zTf7QvbaHfsxEyShXcDO1fMxg4/h5xgkGjUvHF7JeRyaMbLz2QboPMVnY7eQoB65J/Kt1ZKyWpi7t36G4uiaPPpkMws7eNlQos0bMgRed2eSMAZ6iuM1Fojq9vbWAuvs3mEsZSqMWGfmbb94Y6dOtdTpFv4hjmWaSd5o2HzWVyUlEZP93OOmSOcf1rKv9LvtOkS7uoo4k5USFSm4BW2AZYhQBxx+dObuEErNXOctrQJc7LyKC2kzhIsb5nXs21ido92/I0t/qDs5t7NzHaL8oC4Bb3JAH+e1OWAWsbyeZbGeaTarSzqCsPds9W5+X86lj02B45HFzDEidWMm9Pp0HPtzWEl0NVvc5XWbW5uY0jR5p5WbaseWYlv4QBWx4ZtodJWKNpmM9xmKWFWVljbryR1P8qvSQ20kDpaXm0kYLIrLI49OnT2H51lWXkWEXkQsbURSq3zW5iOM8j5iWaptoNvqYXimw+xaxJgfLJ8wxWIQdvArufH1uA1vMOpyufWuI7cZqEVLcrlcdaY4GKlYYzmm4BFMRmkYY1s6BceReq4QPIv+rJPCt2bHfHpWTKv75gK6Dwfpz6r4lsrBCFaeVYwzdAWOMn86a0E9j16L4Lz+KbSy1a41yW2a4tY5HEsf2h3c5OfvKFXbtIHJ+YjtztaP8Ef7BWa6sPE1ympDBt5VhCRrg8hlyWOenDDHv0r11I0jjVEUKijCqowAPSpaVxnL6Tf6xbarJompWt3dmKNJE1VYlSGUHggjd8rA9sknrjGM9KvzKCVI9j2p9FAHk3xO8Gar4i12zm05UKGDY5YnggnsPak8MfCw6ZblpCpuZFw8zjB+gHYV6zRWc4c+jegrXPF/FPgOeKRpEnkieQY3qchh3x6VzOl/D63ivftOsNdT2UfzCC3iG6T/AGS27gV9EzW8VzH5cyB19DTY7aGJCiRoqEYIC9frShGcZaPQXLbY+cNf0bT9V0+OJLee3mtHcWsd44wUJzsLj+H0z90+uc15xqF9d2byWYhezKDY0eMEetfWes+C7DUt0kUccUpOcEfKfyrhtZ+Gq3zpHc6aJ1j+6V3cD03L/KnPETTtKP3C5bHzpbmF4phM0ikJ+7CL1b/aPYVGqgAfxGvZb/4PRqjvBYahEAMna24D8xXJzfD29QuIhLlezxUKrFj5jidjucucewp4QAVtXPhbUreTY8fPupFQp4a1WU4jt93OOKvnQ7ozQRQSO3Wth/COuou42TkfWq7+HtWTObKTjrRzId0Z4OO1HmE/w4q4dE1P/nzlp0WgavI+1LCYn6U7oClnIpcg9a6CHwH4kmUEadIB71etvhd4oueU06YqDyVUnFF0ByGc9BzXVeG9Ouo1meIMJ5ojGVK/wntmuv8AD/wa1iScPdRGEAjLS/LivZvDvgbTNBgXMa3E/d3GQPwrOSctOgj5NvPCGqWJ/fCJfffVSONom8tsFl4JByK+rPiH4ZsL3w5PdJaxJLAuflXGR+FfLlyVW8k2jA3dKpXvZgKi9alkX5RxTIzwamzvT3qxmz4LdI/EVuX4zwPzFdD4kQtcayivDE5aMo4X5hgck4Gf/wBVcZpUhh1GFgcEOOa7/WEik1JZmtrmYX0K5eNwAvHAPB77qEtRS2Od8J3huHkgmvzfNH3eM/KPZm+aunIRbhzCFV2Huc/73t9c1yum2cVleoLaz1FnwVd2IEar7nZz9K6EBI1/i2tj+L5m9z/hS1Q73I4knnv7eykU+XMRiSGTy0Lf7uDk9u2f7tddoMtytnMsk1xFHdoS0kbDKsfmyMfN/s9eATXNxaf9vv7UrkSRSLJuDY2gdz7VtTznTZjFHsaN2LLGHG9c9tvcfSlzuOqDlT3NGLX/ABPZzzyG4R0lXGCEZV9OMDtXG6wkdzrdjcSPMrTRJIsMJIyenJHbA9c9hnNbN1dSXCBDuiR+C7jB/wCAjqTVWQIbiSVpreNo/kiByCsfTbv28evBpqd9xuJZuroDT5priOJE8o7ZLnbt6Yx83P5VjJNYfb4HcEzRW6w4tyUj6bufMzuU7uGA/Gi/EtyQht4r20cnhJ0DzEdAPmHT6Uy10K5ayEk1szTR52fusHys52HGeVyf19BT1sI0hc2+FEDR27H++u5R9Dzj8hWHqtrc3esWoZp7louqxTr8vTqhO79K0ogkaeXKu044Z12kj/Ed6wZ7xdR12WBkSeC3Tykk+66P6huuOny9KQyb4gYay0Rv4vs4HPXoK4fYxXPauw8fTK19Y2sZ3+Rbqpx+H/165Fm2oRtx9aS2EQuBtrX8F3YtPF9oWOFm3Qsf94YH64rJboBUJZ4ZBNGdrxkMp9COaGNOzPdXc79qnK1yXjTTpn0u21TI8k3clr+IVW/xrbsdVg1DRYdRRlVHTex9GHUfga29F0qHx3o8emyRyQ6daPI7yR9ZZW+o7Dj2qqSFU0PEE6Bvxp6k56V7LD8GjbsEuYftSsAQ8VwUZPYjofrV5vg/pir/AMetxn/rq1diatuc9/I8NHzct+lRRj74/wBvj8q9nufhDbnmCO6U+8uf/Za53U/hRfQCSRGuIbdBvyBuJ7Y45zVeguZHn3bqDSjAziuztPhLrd7AZotRKJuI/exsp/LHtZ1lVJRx9OcHKRUkFKRBBaSRbhgMOoaQjiGUlG4Ehi6BAaWkhu6W7kZKujuHcBCkBiZYPHt2z/73bJ09uy/uu/viF+e593PP8zzfr3I6lmI9EqqmxYwURWrv+QefHjuvi3CI0ntVwrEU8MjOfVZyNOk/Eage2CnZUfHba8il0DXM3HZl8y29mzpbDsIEjubAeJciOr5I363qty1wE3R0ByuDaODVz1vAQ/FUE3pGaQlNk2W/5/NXLl6M0nz1NEiFrdcZyhHY67sEO/Bsf07fNuFSIrzek/Qkr8/MfxN2lYLmiNgERxH+05p8hdRuRSDDI14oUMDU6+dJw7JYgD2gybuU7U1QJIoZhrLhWL0FqBpPih0DrrKZfBHfNoFR/NgSKKb+XiE41BcVlDg456YgiL1by3N4AfW43TkLUry8UQ884Fl0t7OUWZAW7Oq61KezLGwSri8Tngi1O3c5UdGUgrFjPrLdaN8CNlVW2bsbG2V2x2Ssd6/C5r/vhSV6cAJpndLJbgHJNVherhlLpKh759+e8dO9AnDIVejpo5RN6EnRKCrHxNP62/cNepq8W0BHmCjCc+MWUPn2fKjKFBxK1YcZ0bkFBEEuhaUghLxQA3PGXuCmgmga0bXgwNiKdBRQzukkn4pTgVwdgsj8/AFIWGj1fFWbYfHB+JFeDvLtQwyqqSP41alQ8y2gTbcdSmiQ79Rqz48GlGkarq+Y8SSm+x+tWyD17AIhhYgbTuiBHmFvhbDlfccCKwRqAgf7/rN+VZ2Klj8pPlTpHVjk9L60yPMN0gDO1cov5p+9KHTnpka4I3DodwJCXUzmv6A5564aLhvuCSeksDwgcjkcrC40NOzPH/gkNGMU+0bunoHiT6aNzt/Yl1/WN2drDJfaH6Y5hhR5g5Vb53hHXUYcyBPgEZKJjQ/o38HxoXQ3CRkuQ3/FM6t4VctzCK/en/65ni9Cg9YdSNKzB5+zl1wuD9GV/wASwa70GlE68HTzxi9j8WGmi3/0VfQ8x7Ybgt/FIOXUJYmdOTEFGY7LXj5x4uwRRTNzRMYm4KGd5TwHYE/nXGN5xbTSD8kdnPQ/MLBdnP1vbfmoB/cB8b8lOM8p8X6Ej0gG5jU4c7040mGhjHL5s1abnzp0tQD7NOXxeIGCbmWudbaL0aSKrTVhcNOA9Qu/tcXYoZogd8Dh5C7/oYuByNpeFAvz0IHqQ5AwXyipr3dc/E8R6yqhcKmEmc86OQyMpuz3qiMetWS8n40Pjq8A6PZTlwxPe07giRX0K+otpfpuBT6O0fliL5neuEjMC1/QM9+8BYTfFP4QuCdSBnFRYTrJViCjqN4ueALJq1HQPVPQMY/Rm5GhQMoV7R/Qz2v0OFKVVZ8xnQHZ0fg2yLxN06gtFcs9DpXsfG4kXedj/pu9pAG/RJgYIQ1wuIjIMIB5gq43ra5B7ir0E8GS3km/BuDDFI6GMweiKx+XukhsK1CynckOKS9Vm70+IuMsY3mgOoVYoznWQ3hesdTW1qo+QHXEhmM4pCTZ0jejNLhdpRwVlQje/yVlnk7LYlCSWzLAZK35ZUnlf5QT26cSOn/0Cbxk/HhBjkEJm1WvLhnsoeSQG+HuRMS3JnjmDkflHYyZsJI3tinW+sojYBiie2Ug39OuKR8eKYg7L5rqAk6QFeg+t1SBTtZUDLKgI3hitZFN7HFk4Hl06TM2li9y4ML16fFAKlBUu/XAoGH+ksOcZFEq3aBjqy6/tNODKwh9+OsCszcfJzxcy7ftRnpa7FCUo/Sy3EPU9EWKakN0r5LSs0CAyThrOmrdMA+yxYXQA6F4dhASA8t5rLKckIfjn3c/3jOvGXwPOTjSsZ7hcfAU2inl77oAvgYtiVzg41PmCB40aq2peLgn2D1dAPNKSrXm4FY608juvz66meWah43G7rwX2Y4cfjXckcfU4/8ZY9dnWKpSk93wFXjcVgSrYgBK1M63zu6kzYnvWDavyXPr32QuUhrPv1xK9Yr8aljLNmr0EHDoQ1nGGjT9co57qClJX/7ZGQFFI03XpjNHcgrVy00DWhAncF1AgbMvumwxULOfRZTcdIjmKw3pMq/fwQcDXHzcPYBfGwl7o7noSsH26Rcjl3UIch6gQLmA/Hvkv0J2/IvKUxr4yx7qGFxA9YIAl40m37SuqF2GfRE6/KBQ6RzW2/nAhraxV439MI01bOar3DNb1gbtl0TVKOQqzCVkqnwfdt8dQoKcevRZuSlZjJkkoJ/zOlDwnkCluiwNPX2WxLz2BkLK1pRkijsURCRnS/1VFI8MOQKXwmzZBwTx1D+NZs/ny43P8Bzj+Y9aYKk0bLhCdRoEDgMRBasM0/o9g4su6JJnE+6tlqnlzwhXvSAS07lJgSUYmPUtQMbzFnB1YEcj5CDysXfB6BbQpfHqbwUtezUNW6+v+C0g1Q9cASJIKVpC8C12xbSF3xcAMtYHRHP/+7UGkJvaHygpyzaRoaNCc1wgUDBDRJdnRinFl01oJ2JbbHv19Ct5g/7w2fJah8g8N1j99NFuDtPhyrbwZYXf4Om33qunMnxp6Od/K5WceztscH8NeJdM1iTopLhmMErHqpLSZD94n/SNOfoPz7F8Re7b7wXhisvioRtwVCd8rkn4edinfV/oItvfD93RTkntUAvOeMObp/WK9wrad3sVk2Mylu8FXN71wDm25SCt/aVcdctYZmPeN5E3ltKAii8j78IcWZritk4Ln43cqyKQcuHFOnc00X920xedQ+Repxfo8+SNH1foYcy7xKzZ2IqxwYk5LvK6K4fms2uz1voTXKIjmc3MDC7X0T2z5t80xJaIgllWEENA8EnpjXqhVVv0nPeE1V1/e0VH07x8C/BDVES9Rqk0/LoXhDgyuH5qXd+RXS3Y34h6a2tmxqry9z4GByMx7WgR8T6Irbnh69Ru/O6m5MQ3zD4K5nIz13dfMyRYBbfVq+B953CAdPefN2Y/v6krrSNStHymfi+UVxpK4cJSpqVdjtLmgmUfUlx7EwrjObeELiyshpmB1orhLXFTj/e7Q0RmTRauTzPLIaEY79yxw8BWf++5hv1cn75vflG7qm8dqX/hbGQhjzkrQ4jPvier1DdFMbl/lW7J22EU/AvPsD4p/0JklH70ZUiYNdEIOAzHc3AGer64Bdj4nj9LMAxgmWGZEJKrttVSU9/jc/xgWuoPxAnCqn36pvx7rCNyq751vPFIUDk2abUeVMxwC8jU8B/mG3QugLaKbqq6NcErOZWpnX369dIxRjo5Pac6RXjZGgL+JTgvYZWrB5d6IpyoiiLUEGb6kKt2soPLjpbxO35se60QX+XsIvNzmR23MbZAGapDGfamsz3Qy1kf6wD8z3Kd3aBHfaWsr15KxGdbX0/uS2Y5kQ4gDAJvAVHuEQevbgGWek+2rYplLpP+wdIt4KJs7pMMvbcl6E1JUZSv2c9VILcuFP08i/EWkG0MTIfEUvn3F1kOzm97XBIgBPb97/+zoGMapAtD3TjcEVsgLsZ+DrhJcnKFuZeDgQzEI1/1lvO5F0NE7vJ4UeGZUF4wlD8kYrpovKUKOVN2ejhaqZ4uyuD2T1m99XsHLdJiS5tZP3H8pGQjwCI14CnS+BYwUg67mriDPeFjaUl6Q/Tn6cjRNOOmW4BnPhhKS0cvkikmk016UpnmFNpBlaS+wKqdRbIhi+EsQfJv/nU16PwDxbbTXlGmWD4PkEB60wvXz/lL1WApiraTQ3t3po/pgL+hJxVOSG1awqtlLPLfy5G5W8B9KUEyzG9Xxc+WuGibttawvIVuIH0dn7M7Kui3hhY0zpANjfwFRNyNg4YtCki1TVsqggcR/6jy1O/lSTnYc83ywgVLYWoyWGSZCImT0PortLiMXfz3JUvs6TTI+ElhS5XDJOy0chpLCQkHGfmAZiOQWpCeqpNuapEp8uNeNHvrMRfvIPUtgMH9tGsaikEJkyMPrEjR3jjnMfPOAVRIs8BHdRmQOmDPd7aeKiJF8YZ4f2pImGR17W9nxOnUDL1/PO4twPggYjtDdsOoWmaS9LSyFhyyxmhLE98SMsGHh/XTBnW3A+K9GjH/7PbyvoelWCbdAsJ2s54+ePAPMtG26ydtTPbkNhuvrhLdbuadqHogRH1iDYkYfUiY2t19dPZSDy5+uOPSCKTmaM/Ps2YZiZGghskfMdt2t4BY+QDxlZqleLfjUv6bedtiNP3JxZ+bwq/0FxuiyPdPwfjudNbaQlOqZQvyFFi/qVbGCMZ12ounNHdH4ZSkC0UapzUAt6ccOoqiL7hAEVk0dW/y1A0gRzk7AfplkJMwbydq7M/GwW2skMkX9cE44IC/asP0gxvHoxutwVMjoya8QdtXDYC76j1oP5uP9Nj8zvqYN6Mmw/K+N8bNsKGDZrI84lhonyrGb6T1enovxcXAU8o84Jl34cdh279MfZBT4Td/BrFsUTUseg/bI1Oc/lKek02XzxdkNt28q1fROFlLKundHf9IfW4zw0EhrnRBxDsYyMSAjMpbb9gMlK4EC694v+qbWLWl0ruich0X0kKQrYhsM41cX1TJRnS3UIhgQQvkg647O/OSZX6CtbZZZ3JJ5ceBw8U0upc32jG7ZInvY/TPx0BGmfmh/mlPgdIz6+yDKOCm4VNf+fQiY4j1sgpcleDaMy6g/DPEsL/p20DaB9clk2632AKtY2o8FHAJgO494fnN9bTfAyPY45tUkCYHKTEdr2vAxNUk9YqT1h0jEHMtHPOak/Sz7M2OrjDKD8lMDKb1Q4x6KVSJ2ZjTatKREGN63SvafNTOtQX4J6nyZaZed0oW7wSPnlZt49SFCh7ZEugy4cUIGdPhDpwLuun0qw2mO+3B8+J8EWw0YjN5QhZH2pLQS+qisZNVOPQ4/zKZa6dLnMFl/lT4u5eL9Igv8flvDhjnOfpQ5Guu9qcCiojSUnm9YJC2GhE1llwNP71I2Gpera0tVYH4MT/w9wzF6yYSfLowrzTrHtIndjZxyaPRGBqs5nXaasTG05beqx99RYsRyElnKZg/782lGNAao7QscMj3Lm8+A2tQmQ5Ckha8vo8yOVN6Kf4wAyLBS/hruQR3ryMxfUM9iHPDRLnz3b9HPw3SNU6yONRiC29iDMX/V7QIxyaWV4xFFnK9ZILslaR4KoZbv/ZYAFeryoU6CfZp3+DYF75tInbyWAHBjaJLIyllHxIA6HHkuq4JBrtkmDu+W3xRS625BXyYB5ufSJq2xNI6x4djUQCFzbmOb7nxjJQOKJkkp/NY9ZeMUbCTyiJ1JNdmqyBqmwXtizN+ZPpdDuB6Awlsky6Mt5yekid8NnJmeXJgQqGpQGwhlqBJKKcZCHyY9p+ti6+rtusjFqVU2RSdv73EKuBtf7vea6uyeVguQQ5+h/acwv8VYVscZmFhSVe9T6iJsYd7R9oYiLOqAcTIL4q2X+Ro/yzRq3zEJwG+v84tKrCsNKwMFADerA9X2ZGth7+2CxbSXeon6M7qT72oVF/zqm9WyhP7aPb6qvKgv7CkqOCm6yxJVUgRBZousnvcRL7cuRQ+kCYS78Iec/zw85leGnHmcTY73RtG+0e8rLVtcUvUFjgD8A+ExJLBcFRHfRnlsDqFUcfmRNw53zs9F0QktUVU/qMkAwINl2mHuyFX+Wyhnz009DVvF0AzBpbCcGOmm0ycrnOfwUtRWrok5rvXFzHsqwrihxr+pfZR5I5sWj46UgTgS5cJqPp5h1GN7neN7Q6DpDhvSXXngKSCe4BeaYU3EtGv8qPyVmPUEtpenULqpDG2+qJPhhs+6vE6rFe7JQGhTgMwfhuKB+ET8q/Zwm8Yw8uUT0vLK1dIQmkhSW6WbrjtZURRkeRLxfjNu/oVfAs/8Nt7uinDanFL7GoB1zRkPaSrTqoXMrN+gw74uyuXZwR19doOjITDy6DREUQGjk5Fdpr98hefUIvLA9UUPasXY3Y4AwA2nPSlYu9eXSOVd9Wx0PTA/CdX70mwaFjfbMEIg5Lhz62LMnjnzG5qBrRFJviHEmGF2JmqXXA6fYKjk2P9BBKsYmLUl2aa/mv5S6IC1wzvn1SsQTl1nHiVAZIpT8V/K+oiivklEXW0/PUASwCQKQWYee8z01tNOYpwin6zYRpFTh88r3wfSj6awKGuoSMtDbxPzoLjmsvSh8qx3ezdRvbkvZZiJeyA3Oj/fVRaDwTQhvSlsVS3mf2KVnWIC0ia1pRlojm8MW7xR8dLxGtsE/xoQEidn1dlB3B4UzrmOlgMc5MBfcsWbjBc3cdm7KP5ZtGAkAAZ0+AMFry0iJIlbyHc62nc5pP1KPLc6B7snmKMtUijylWO09tD6c4qk/opZnn9nHqlgKkpocszlRbRFRm9IGinJEhammvUcq9Fjbnvytf9zZJZo0joLaD0W+PE7IAuRQq/SM4mqaBngXVJ37DLZSDdp4RGmrc0R0NdDMgiJS+eqkW/HQ8fVnLqEesR42qaq301jxvPqlx7Wzxt5eKToXbKHX7lcgkLnZ3tFdo56OuW8I01Q1OiPLggi1cyKvdh167fzyE4m/iLkuIRC+n9Y58PptwAH8FwPb0lZQ4axFQ9rzB7QV2qOHF1jZXLDNmyERoicfzhZFTPWTXBJs2h76dYi4GBaxfxR0+PXz5j7+tPHEsuNYmX1LOqnt1TMtW9BrbdVRyjm/coOtIl4415nZnKV7pzc3M+1vJMrG0+eL7H0s0MhL7r0+4pHVnehYEgFicWyMcGNYTAic5Htmy8C6BXhitXbV1140T58DoymOu9FsmIlHwfTpwRyxmiobndfks4HIaXHPC0VhHXH5XZZAU0LToaE8ojF31pMsNSeyKTFeshYGynnOOACKRzQHbJIOLgp/0+0oiVpaTfKU+ard2+2s7r6dGG9RobD08p9n3tm8FvePhdeVdO/1M5pQvULpKHuK8BtKmc1ZGET+pQGtLY7sVEjCbDss22HYXdWxJsjjqv1Hs3ZTUvrF+O2PayMuMT/wPW9VbprfZ2ehs9LHzvDa7yAn2DRAAFTom5uUOhwaC9LXUcCz1AApXWKie/X8vMDNAJv39BgUPs5Tza92ZA1YPjJ/pGp9TixUCO5pvifUBX0QTOf6Ol8l9DlZewCvPX9lwDL8Ds3Am1MfWHMfZukknzp8AhT8SZvAX8CVGliv/hQDd0x0sOWEqL/7mtPCfNs2jzKAsFxpjsmRkNApKcTWkmTfnHi9cfW+qILYFIhJvoHXQKcaG5U6gcHmeUKj137lSdz9VU/ullnXIL6Ik5mb/a+Wd3FLEBDo/c3GWKuAPmdvloCzE1tk2FMPc2cnN4g7hAI80FdeXXkd4b+QwUQujIe4Hs7achpje+uu3/RemPFcBDiRdfnu1oTY3drr0FMCtREBF41kUA1xNg12mAmv/BORAKbrfz2WGJZyoaHM3JE3z29e46ahVU4HnTR3jlXFXTXtjLsK0EL+YSXbCG7/zdFPAYzQQMRasJ8FnaO/dv+XnQZJPoBNHcTCe1zpjXNh0DNWUl1QAGqBHDNMbaG53xUaUg6CjhWbmHY1YSL06/BmMYT7lEZplwnrxZxnGmgOusiXsVJy5jGkJCkNLdocexzV9vUoGt3Y1WpsYj35ir760cLEvkFzVE+bzVRLt3jb2eLKq/7hZwduT1sqcI+31UAmpV2Nb3S53H4HmavgmtcJioaKoITB1C62rHp7a3yt+nFPYLEnm51do6cj+x6jIs17j7XoIT/oxfS1b2cCeXZfFW9e7JReaoaz6ttsKe3wFDe4+UylErz1UpJuX90N5nQe717iefeFKIMrOxwrp0MzMvmjhYNDjZzaZETX0DhKsIw+cUGQ8dJDWpWIfZVjQvzNRlMVyGPMygH1+FqqunEY7Pd/Obm1FKTU5ycdILDLac/kYkn/cTxg+qV1dMQmuCskwKloyiAHLUgz8ldOdgljYNE2rWrL0ro9fNs1bXbbmEK7FuZyLeXSW7tXUN7q2dFt3vd0w5B0lAJtXQ1FtAV2QlROe0v70tQD2xdUdngZfmTSj4nWYP1Px6llf/Fb8wxw3tTUeF9WYmcAjqZsLPU/NTQJBpOz6uAjEZUL8736htuiJ1Ju5l+dXWkbeg9Xth2pvjwWRpu9YNt7Sx1jSbpPiBZ8TThC+Topiz2GNdfQ608C4bpk1W5PDI22qHN5ljCVT4xQAkex3VJ2zh33qyKOqmnWUmIP6uCj5GVW7TON7YY/uRAGLkU6OyfbT2Z1pM8uMjWzrc5Hgzp25qToGFZ5jdy6qAfJ6Lh+y5QQk4Z4KUgHM8D2b0XjjNxSEpISXPfxCy/N8FDn4f+cryEF5ZM4tWOdcemAnpakJqlEn74rmFcryY8MWjD0e+BLCqxfaK8/vXTFzbe+CcbNLYj5u3gAphY9G1KvlTeC/RLYBkjLW/3MnNyuj5rDfThv1Yvm5UdC3lp3MhHBcjopDpmff7+VdbP5LfSLhy6qQXnaSZgbVDoid/zAnTMWNj/V3Izh/TB+jEpbCQyDoVABHMqLZJZwknpFqbYsYj0+19dbuC8eiLo5ioevEFJt8++/hRn0KaoEIepb3mNCse7kr4bGpamCK7vxxfMrMkaOZUdTWkCdal1aTv/jXmxA2h0boDl5oSh+MGacZ8IKkLl5Q+3A2HeZUYR1bkcYNctGwNhY+rPjO0t3EvQ7kJlW/su9bu1Z70hwqMPR4KkLUYxBqgSH0BA0jwyWmbOOlleB7VjRFpAr1rB3b2UOh/4b76/yuc70pKG30W38lM/MD39hB4aNCIb9U1tn7lDieITAxWDuZB9h50CiwOcXLPGWFJ/vynkpt+ARxRFwzCutKv5U1kB9P/XFRlCTs80ZioTFvXDNbPVF+5q30SgHG9Za08q5xBBsJN5YKUDA38HclSnX7NOFmjLE5zjl8KzEulW6Lc9WPqXZDcddUvmNVFpoQKGyn70lc3+5+OIUflgLSdZBetBwOc3yjj6tucvDIqvxUGS5uP6TWdDrRzW7FXvmiIuQU8anvNlS5KdGhbaD4vJOrfbaPi5ubm3n/M9lX3wnNMZ8D3r40gh0yncmxGHLKEE3EsHqkZd0GUkWVLpA0S73/GkHE3l3uBSWSYTLzHNZ8o0zIwrg4usf15fgvIsj9cK2rceVQVsf7QqU2T09SuxtjABuXF3Sr7OSThb7FU2DNYOp4LWNG2xb8wyRw/NqzFaPlNK3MU4UPgeMB5WDNPWFLDd8tHSfkqj+ruPxabzy0uc9eU7fn2bGry/+qyyCW4IzVnBKq78T6QG4MjZaiQXuAz+mVMsuf+KU4MvBLYS7kyKcvEjyzaWPuRG5HVr7baErMno1gllrZ0/IDY7fULsd+6HdvlI2O4SjM49u0SS7psLlYxjmxHc4EynC/ksARMYc9SY/z69Oa9ICRonoBYIltbRki0yLM5vM57fgyCNUAn40ulRMjvOpwztiXqLHqse64XsM/loqpAoQtEyBUM1jLzDZE4u+Z5LdoFJFZqeu0FeapAl2nE4B9RjO58xusH30uGA2PZrV3+BtsfRMrcR0rcf8rEebH32BH1duXjz8HVAZHtTlXU/FuHE3jPXPIR2VSef2ffqCuEWZZJwEaGfNbvtWuC0bLi63PDy1ekaNKGQJa0jLJW+lz0IJprtm6Vs1c1siC23JnjkMyjbAYnKs/bSGFCVuSpzVccKN/f2cb/82L2/zz0JLcgD2wDuGtErk7QKEWl934j2BctnOy4u6+eollOCcOtkreWVqu4cdhGv+wtSQ/abRpLfdL64O7kAnbbanaw7zKlP8V5eQaS8zw8CQzFJuKc7ltkh0kWkygxuF3Pt3pHbFilfV1Ml9ZScZM6Ir3JQOA9gbUJTrWd9XWSpvcu9V9AL2uaUAI5aw6Xxz+1p10G1zAcC3riOOKEjHW5js1MBYZtk7E/kqgA2/TX3th6hSEz+muY+/bxxVbsm50OV4hzgHw+ShZB+89W6L0ji98qqECJmjt1RUEsT4NFoNVDjDHxl9FcHU9dr3OvoCUPtBV2ZFq0AQtNluhCyc0VcCwGU7zjR+/P8PpkQTfbFYxbg+lUPBe5T7vhtQn0n+BEzTUX6NjPjSEdRLYSnP1eVZQzVbO1zHjXD4L5B3DcBk9dxle3hQ8jCyh1UpsBjwZLrkps/50r8X+Pg7eL/wlQSwcIjMfnTCufAAAvqQAAUEsDBBQACAAIACS5a0MAAAAAAAAAAAAAAAAvAAAAYjU5YmIzZDFlYTA5MjZjZDI0ZjYxMzQ1Y2Q3NTdmOTdcQXV0b19ncsO8bi5KUEe8u3dQVMHXNjiIChIkCJIZJIiAoOTMiEjOOYOC5JwzoyI5g4AMSZJDRpCcRiUMOQ45M+ScGWDC8vvq290/dr+q3a333b51qu6t7tt1n+4+5zxP3W7cDG4FQK6ioKwAwLsHAODdXQDcPEAOQPjwIcHDB4QEBASPHhESkVCRkhATk9BRPiGjYqIHMjPRMzKysPNxsrC+ZGNkfCHK9fI1v5CQEJBTXFpMQIpPUEjgP53gPXr0iISYhJaUlFbgGeMzgf/XBfcHQEGIF4GvhI/HCrhHgYdPgYfrAgDvvvMB3v8ogP9Z8O7h33/wkIDwERHxXYN6csA9PHz8e/fxHzy4f/+uNuSuHnCf4gHlM37Zh0+0PxCwelAJfE7OJ2R7W/OXWmfsmF3QyvPLI6KnNLR09BzPOV9wcQsJi4iKiUvIvZNXUFRSVtHV0zcwNDI2sf5oY2tn7+Do5e3j6+cfEBj2NTwiMio6JiX1W1p6xvdMSEFhUfFPaElpWe3vuvqGxqbmln+dXd098N6+/vEJxOTU9Mzs3Ooacn1jc2t7Z/fk9Oz84vIKdX3zH1x4AHy8/7383+KiuMN17/59/PsE/8GFd8/vPw0o7j94xv+QUlab4IPHE1aBz4RUb5Pza/4+YhPUOaa28hwjesoutMpx8h9o/wPZ/zNgX/4/Ifs/gP2fuOYAJPh4d5OHTwEAAa5uXhR8IvpfGVfcqrw+BCvW8qvYY6YZIkrU2TT1hY1KR0PsQM/QPKnxFTlTDwZ+PkTT1LCwq4q3VOiA8KuyQcuSg/Y+X+KjHZ9Uv9XwXb+dZO/zitn1sVp9tMu1pi/d7YlvITtGFUq1ukZtsQviFjdqL9KABd6M01H5VSn5Q/gnEaFCwCfwOXlof2cOkx0ksp3Z8WaacYmToPDJua42kArvKidy0n7D6jJZEvxal+SPIfkSb4Nluxc9xlzxokwXtaX+xm/XoPyiSRYH+K3d3znH1pFyYlDWUUQA3bJw8jghUASkls/iACtvgRvGtcGyY35e5abYx5rYAUWW9urkveiSCCwHete7TRctd1bNqBkFIWfDPo8K/TyCHTBAolLzEyBJbHOioFtexs8HwYnmNKq7IAk5747Cs+oXOEB4VsFjSBiwSAB8IkyHyinIuw4F355w4gBPFLmB9YoVWX8kE4cLRf8Ehvqsb63ZxuIAoHHwcjQIBYnv4NiOxFqRgA6+5qHVGUssEBfVB+TSoKN8TdPjEJDESQ8qucAuR4+sQgcczo1WGHuENPkKbouDDequn5E5rQe9brN0G844iD64nk5WPMFXcYVMQpHc1RelGT3plODyqZemO555yDuQZfuB5Rafr7Qax7/7kEvAWXCAT5Az+zat6qtXvPOY2W84gEld7rMsII/dtv36h4PkbXzdyGb4FFS1N68wZoX1hHp0l73bPLLLBe0Ipi5M/lbWnQODNA3LM1vdxKzDowo/nL1AywuhYsj9AbYZPEAJCczenmqTIScw6pkrDlBpHmscDkvEAZiL++GD8egYAWkn4K0Gq8z1z5x3YJKwk2JbyUJ7xvEpM9HbljjMY8dTjSqJUQFHLryH6f/r1fr/h3E96tZvbVX15khcffNEWQCqq88O079/zvyz2UW1yzElCfrSnzAb0tOCgOYQS8XmHeI3YTmhZ/nPLwXSjLp2qtFyRA+JWUDVpzgA/aar8A6feTq+VCVmRvFucWCFv19pbbETgA6Y/hWkaidVLc5Yyv6pRMq2n4vtWuEA33K1S9Tm276v4QCOAQrgS2v9w58t9WFeS4rPOBlYFf5cvVQ3dPrJWWm3a5DkmL73YNQ33gxEcH0zldvPY/3AQn23d7nbwENkGvHMQbJIPC1y5XNZ8kmdTq91Y5hu8wccQGqFEHSyiU1zZOLUjMSaN+bd2O93orl3BbryreXlme7x8aumqI1Nx8wK3s2WWVNf4zE6CrbU3PIHB4Ab3kyMtRmKLmF76ywLexWx0iYKBrsaDlI9P0uvPkocFbwgFbVMxYCj0kFOQUKWm1zgX8VgFOqEueZVifIXMrRvVbr0myL2K7GbifW3PnYLUByAcCkBjmE1V1jBASZUp++GK9DfrtPeC5PGkGfo67ane52NucABOkq3E7YIK5ZlIcE1+3yBiSWTY2gQs8h2OsHeU3COkak5N6i52IisuGUiVRPBDs+w9r4+D088L+2JrmhU577Fol8XLtIcAT1inCfCa+uASjRobm2Pe+cNjcDLbvC/3Fz6aeDPNC9UCXAQMbAKJP+FVEsKsYkD7yMseH5dc8vEfbJ4JyFHgLmxPIbGywpiq57hAM5TxTjAV8ku0DnZn6tcEJY7EfVOeHVqjADTpogVui5c51PJiQA7vEKfxWIxla8uY8AjYrCjuQnYKuU0bGsKiH6kefLDX84SdLpDhwM0fr2DLl64zpgm+QjzIxJrLIcDhGagX9CM4gAjxODbc9iqDtlDVCw2WA8HmPe+a0z2VUoBtMmoiWm886+YwlwZufXS2TjR9C4vF2fwQQw4XPRARH2q5+79+Qc4AFGQv2YXtyAmfWtHyA4HsC1h6Aw89Rk/BJNCr4UZx0LCB7S9P37dSbyqG3jOfLmHpX5ivC0QgiFWc6usRdi9m4pE/3MDE6o/G693B6/TlIBXePJ25JHrT0ta+E2VjtvCNo8PISFdtFh9fH+7v+NPcogegM6HZh0sBrTisKf/LkBLDR7o7rc9ercnvTCj3oKxfcZJGncZsuPo23S/140YgVYPTWbK0WmMBrTyDXi2zTHs4A2YPhGOA1Sr8CHOk8FH+arp0mFzms3v/T9QYZHdEAT46Bd4SxHNNlcALjkpWr5cmqTPp7mPAzx1WNto90CN9ZFf/n6pWIyCvGqu3jFknjCptcNeCzvyr5W0zDuIAi969vPvFvTnihPf69tJlg4PtF6Q2LfyIRocoK4e1ZTRmeFy5CakgwNoa8Gibb7m1Tm0dHdIZNT6AlGHu9E+XASKpROmTYlFIyj+4v0Mz47am3wXdEgxe0ytY03PIr+E0J2rM99riRfsETEUo7CcG8o7VKvEOOVilzN7Zol6yezwIvf0iySEx4aGY3/2h6jXhl3HZKhsJncbnc8IRy2QnBhkaIe3SAe8DPT9BL16eiViNzV++g6+ogwsNk14ZG15rklpCd9uVKmNGRqzHevuzi28nJSm00RqmP5doLAwuZLh+oT/YCojWPIhZgxUUqIZ71PJD1uzWd0rQYAHlDgew6pRCDHh5rLqp4E3GomjiE9hFg7QYNVxO+LNASGCcX8ljIJTxa8TvpxgguQA/K1aJcFrvZlJZcEfBT8SvD069f6WUvFSZRYPAai0IS8ABTH//VbESfUkBurjXVPat6J1b3GhQkWZBc9Mob5M3XuEkayegOyZlP6QCqbKKH7DyrJN8QQoa1Z/sLQ5l8ddvUg81whVzDLwsOKZf2dgzfhS6Xr98Gj6mNrAeHbYU51LfNedR2O+s9HTJKsVGvOvT8FkbaeBJPBTAHqvUIkPTvJBImFPlzxdaLQ4y36jHdCHLs1YEju2SBZvmDioDlYOySbNa/2a5+x1Q1+1JHCCOa11CHTNzDdtVC9prbnJG/99WYrm3sQBDBpqfUV+jAoHZQeYuMzjj9bZ3EXQxC2D+X+Q8CbSII74pIvmFn2scRU3Uv3EtXS4FMkwRYB69pLgjNoCBDDun21uRbguNzt4YIUsCmdJdQsa/SRpGkcr9bJGqHZ2EkbZlG9SHuhKHH06wAGmUTGHb0FbcUSwEeFYms4DZmH2nWEc4GJcEbSqk/jYP3TiyHinBokNbAu4cwNIfr9qALuZtfrBU6zlsWqt//zqgjSfsDJs5Q2Yo0gzqgNfg21M2LTwgO2ui7KSvM6p8sR6Bw/kbTEZNgyieMIZybJXPp94s8WYt6qzsSRfzpt/TUPWFY+n4SL1KIgT423gtumwd8LtDC4IlpY/f+UqeDOlihrotMZaUfaCZz7DSkvgced3LqP/tJAfB/jpu4cDdOuJy13nrdlnt8iHPtxG5ayNgseC2RjxG4henRe7RQPJP656x/rDb3XhmAfW0Kg2HAB1ebzUKvpz3hYHWFPXeHXRB5r0Z7D8sDt1SoaBqhzveSxBreZR82svOzHqMSGuSliFMli0DOtA2tk+VdCiGvjS0VKwOw7styKti31IC5bVqYQlsINaj9n3sOgZrCsXVHPQoOw2lOMpItjv1VLrOOxpMiyzhNG/X7M9qIjs9r3mGXWdUGJUClnq3+QX+6QL1tcDipecXe9lwKRGiljMPhjtC/kWaJZBlKNzGweqRdW07NJbYXgJUNqYvLXUacMaoKoslrrOGwx8MeAgwQqGBX7HAUZ3Cjrh3GDkRKdD3pHl3RB16/jQ2F2l7a/f0naqnygETB2AiTnuIrz/eLAmDiDbBCLmqPSyQbpu/esH7V1wkWbEmVaOhBNgOuAYB4mc1Fv4vs0klrAf23sCwhC4nOEAFm8T92FPEq8TTLEiPtWYTKQCkGM5/I4103iAT4RKi1BnBWRkg0Hc5l1e6JLL6sa1x6nYFH7Yb7QW7IyhDu3CrXSXj2iUBRSfVttaKBB+MrVmh4y3WNLZH1+3NIa/S/9j87POZYa5qFCEoJlair6y/eDLbqDZUJavoQ0bGcXV3VSHeJddDth5qxQd1d7GGNJrxp+3pjVmmdTp1hST0tqakaSI4k8nRPyuw5iuMU1WPPkLxmfvZZYe/8UOLDZKNXfasUnme9BVM6/pJcizNRDP6mxHgMr8Zl1NPebvOr0/ZeL8wLit3BvIvQV6ZTlVmHviGULsrv3NKn1TwjLYMCo+3ww8PQbHhqtLXHXruXoPRDKXuy+jzX1MlqOFRsh+um3x8JBUEIoqgR8vR1fJdnAxlBLtQNinCaVnR7BiTVVik+W8OhLFGnHeLumgVS5UbhjZj0XREpKhO01Cb+0Pg7+3BRMu9OEArrewYk70y6yZyKM2Hu8OVBJY6CdZrG/yiUyiDw2mHn6mAnMy9kaDV1L3S2RwAD80XjwSRG6HYfvjx4mIBWKn1e4IxywcHezPfSKNHUhcL6hSPAlSkGqvXMNwxOXt3CmW+nyBCBwg+kuiDcG1MPNS7S0oqj2eYPqYnwFuooUDmK/eoiKrv3X+hwDAVqWP50Xo+FZv8kG3wt5ya1Of4tuZLxW378eVFV6U6QRr1aaGE965+9x7cLGZBzX4W7+RI9PgxklexPoOmJXscpXtBvIrl/MYnednHAY64CHDpFdC49GSnk25PY8VOXsjZG9KhD/4aEZeaVfPebdL9S12dFFhpfQxrk7+yRcmmg7Uqfrj67eQ9gwMBn52r4JjqC1v96iSATM7jbaHzK9W9sdDQnMrl/Eyrq1KFlGaf1K6PtY87dE4KUaWogUutLr7WoV60x9DDHWEZT3F/GfAv7khoZzAP/Adsys0C4S98HXWHTnr3xPDkAKPP//L2xXmNQGVl4NV9nWytj1b9C7VtrvO4Gg+bqN65YLtQZja9PNgnrI34DG0ZggQ4x0FxEByMGlrUYqHbYoksIs5/LugCh3i6wnt887Y9EkxM17Ev2y1ZwctfZwD84fpg2qFttwExtdUffeuwhJPME5EDIn0M41kPzWkY5+BfpTCo6X0KXAApeOD9j8XCtEwCKKR5oTNqMcD9dF3zmYKalMnLwoJwwaojmBOJ6cdOlggfhTKDDQ9moe9LIbxOMC/AOlqdAhKwb/38NcvIITCJNCuu5Kwl3KTeECEaSoYeWyDrU+NkxD8Sc3NUSZd/AqZ5O5xDo3tcNdEmvmmrbXTGNg4uWjM2eFL2pnHJ5b0Co++u2xUkiqdeCkgIrMBmsrvrKlwhDb/ZswvC+xUtqn7rvhiBTO172TBhV8i/LCrTlv+LtX/d5q6L2ERBFAd4M4SyX7qT91r6eji4+1S4AoYgF0ZTiVS7sWS6PTTAsKIseARlZ54Zrj6/Ct0sGr08xHtbVjk2ZCDCuPw0Ucvw9L+ikaGksXH2mLa88J5LtYeJWo61CMMOfPh8UG/RdV062IDLtpVlASoeJA8wzScdFdioMoPqNsehTn5Y7+viD4vnge5RtfsN3YwHMBUuKKGQqV3K4JuwJjSAjWvcYyZ+TXufYnw6XFJDotkuSk7116w403IdxLZkptq0xRrOkn/NUjAptkQzBok6HVjt6c+4bzfRlfU+/FjyNs3Jrvr6OHl/Yf7sJH29xiYxUlu/vOcgjfBdebjHZjkrryl5EQAOIknQp9Te6dA0qqQzJf76FR0A4EWXi16bRxViANYzXrCdxfv6H936hq+mfq6Q6CumUogGUQBdExNLZK2WsmicWI0s+DfgRW8ndWHkEo8vXJrfwbUhhysH1+2Pvye53ByX+LdY6iIDLDO1McCtFW9JPNtEfyxYh1Udqs4OKzySEpbKjS0tMQhl6HBNTEk3Au7b817vVa+uIgyeToPPmHT7ZCe0KyxAWbxUyP8wavVkdW5qu0642tYuWG7Vq/WXQVSH9BxrL+f5meZ7h8ONa8/nIV8lwx1STWbgMvzzP4uoOUIAv+V+rQLejz3pmbeH24Qusc+VpD3N6CSECiXhAcNZkNUKe9wDB38JTju4ZnSulZueF0DLXr/6rSIb6u85gayFZBon6OK/6BVao5qShf4EaWYr7hzWU92ffjBUA+Fyjt3I0BJ/PGdvy8ORF1X7QEmPuGnGrf9K5xlnaKEHHo44gDUqVHV3sSasozaJGBkRBYvrLuP6jeqdpRMSRuMmqmal3qiW4PpHdnQvbhpn17Q+Te+754OMUyweYXJR6pOnN67/1jXYXE5BvZhdVFhFytWhTZce4TkjQC6eY+sy/s8fx0MZ9JXPCsaS2L4M/OXUvSiki2qnMO3a0c38a3IsULKvcKhsuHlpQy9JjdMHnWi3/GApmQuZ0cWJvpV8chWS6vvt0fNZSZVVQ38D0ee1+lk7WLPcopnVthQQVCZtZt3TRZnmpx3IPSqguny/yZjUl1alz2wtu2cmpO6WrXLcALqzxV8ro+Q1GbjHRUmgunH0xHebig1l0YHA3UiWfZ4xqSHOoGPGdja/egjolc3Zh6GFSU8wgESacEoyFYd9FamdoJ56lZxDYnmUdRBNKp/lSYwgSTI/2XlEgKTrYO7IpWQ2GyrO4rlGN+Tmk8lNlr3+S/8hgSMVlfkK67baK64rmfdf5tNFHUrp6xMd0WvERuGA1AGPZDyZDEDc1fkMo8esjyri3VO79FywepbGQ+cmkID6526W/JKqyB+5mrcgjLzGqlvm59sS6QtZUnElRjHKiwNVrjLOy5KyVcEm7u4MBUNeV2S2g7LkPe+kUSAfTI2bw6kvfT5TCnzfOB7BpUHfccWVQdok3hIXgkSlEzdklqfOSIEaXI08J1ziwx+92te7pGpU7gb9+usRCsPbEDlAJehyij6WvYhIU3AoW/BSV6lNSr62zb9ON5gShHwauI5WG1srRU1/W8uMV1DYQU++mUWiNpG75a1dr+So3dKW0ZsVrL8ToBjKXEActMqqF+Jxk7xTq3o4fqc+3gf9l8uYAceHOOMFTsxg7FM/6yTX3XZt1JiiwskyxC27rb/ZbmTntcJtRdJKgiq/c2P9q+Sz3pe7sRuYiBBdRIZoxYDO/62i5L6qAbFAWzKLY+/o2r876hAnpYNDuBi5bZZPzRHJrBB3oC3slb1YDBLUQ3R0K9wAIuRMvRgeTdVaKW5nKHWGAJDbZg3nbgluKxJSqk7Uj0WhPbAeg3cPdxsRY6dnm6ubrp9T5HeteYSza8opIWbD1mfEMPtK4D6E5vA8/FhwTy0b6N+KKvmvSGPIpTJutjw7AHrMP/Ce0OiLf7aY1nGsKV2v86rch+r1AM6b/OVhCISu9N7Le+/NYo7KsP1PJIt9hopfqsfX/2d+OoSJ1/wjODY7Y7u66e/48BOH7cq/mPkjzlYQXe4bViES1fw8EgohEm782RN89Ih6uyYF8s4/dPozBkzW487SwWDpVs/MV/OzZ+gRBzbJvzpGIuHk9daDZgK2iPegI6KS9dr7JxT5GWFaxKJZlnGW+tnzq2p/B+/kcox7BaJxGYZy7EArwaI0liPL1caYOSHSNcBj+JBWFlNSRxP4zOqNN1Jx4ucOtLSeep4WcKuFetsHd0mCW36pGGx36j4AtiPXOU1EOpUH+WCft+JIe6SIL265d91z8MQEsWsjZGbqxjykJNOSPtX0LmMb13Vsgc9mmMjbEbvNs9xzrw1ZSt9Hawc7+kt61nYDkt9hf3UUzJUhWoYzGv0dz1lkcj4lWRAWl/kInq4csq/7Lu8YRKpMymEIpjx4dUgsPgp2QdA44kVznfsMz9+OhMMpgj+OethH9VZIpmErRfKFZy4oG1r+F3vjAOMuC0lIvQc1nCAJ1SEN4gM4lyD0yWecDj6EbjSoHn64GcIJDICLR3S+mXMpL4i7wrhguFur8jNELypMCgZjVU9riqm4sUfge6SaOxUZlm9Ai5K+VxR/y7ewz4/TsH8VJRoSIFbD2x48g+z6/ZK4wCVnlDN48V5cIHZIir0oKb+FfDgaUUQmfCbjzjAZ/3bEF3D48lBE4V2qn+TxTSE1iF/UfMdosBg68ZGxxGI9rxONm9Ros1Em82HSvuetXH994Ue0cPGZMHMSLqryiEePWVrA0NdBkaSRpYbw5jdQKJ5U+ATlILuS7atpt/Y412VhEGJtWqUW/eeFA+7W9TmKmzWdcEXfiGE1BGcAQqLVg1e9S5IrFNoVtl1tozMPyPaeizG2qLlyQWJlafSwvvvMqOWzR+8B/0PO0WpC/08G47Tn7fBuiBH3ydEjr4BecGXbhPXo2o5aT3vwPUXf4Yf1dfeC8DbHkITYzRHbyZfPVlu2Kh/O8QODUJWLZ9YY5xM/pHtVz4iHel7CdsRvY8DPFYkRvERbBkt0UULhwSaGxyvjU+qI7JauTGT6MCpieCkDdPfMcRzeq3boG768WDpY4n5rn4fp41nHpOeMrbYsBlD/tUcrmDJovqL3cOpo8jMl1UBESJ0xPseA0B37iJDTSQs6ipwaC1jwnuhRSGQH+gBlgL+yz+J+M3aNdpj/LNJDPBY6fIGshLYIX8maeooatreTqTqFoJ0I79TGLMqz+rD1RppBEJ6WYGBClXLb0Yr0fr23gfCz2uOzSs+a4yku1iYfbJQ2GtEXyLpvMVfVri0Edtxd/t5loesMRSLzUkU0V0ytYfW7815t7i015oYf08nnLROEOuh1gv00DWoftX6xFFIJwE2wZYyN6A+kd4zTHtwYH2brCBSlrAAtgwcbo7aTcFrquCBN5f6PDJxiOb84hjkXk4r3u2ulw41Y5tMNe1kqrgn1vO0oOn9PE0tJAAi+McHvVuJ6AOQPj99BHAxu6pgH1qLit4SykvgUibtpaX6PkIr/PkXmdn4RTH+XAa1Ae09/jjdz+yeyt1CcTphnwLWx+0puD3cPDWvdK8h6hS/X0g3il78FLSaQoL2EzFE5f6hSJ7ceRwgv6qFv00jsKr7dqCaG1npafECQfxCK4h+etrudGvYKWqKj2Tcp2pOW+znkBvpbuXTbWL3UMex1uazoipRjexuMZlJGMnSe05hz4Si7mRzc0z6JsgA2BeJmuBzZfoJrtSfTDz6IDMISlPp/fhcY1C5QGvssQAi30My4u+O/kJLDMzLpV1wKcvjIQ0zAkmeKvgVJmw/N3CbBFtcq11XEzZqAKdDEooa86Xn0UMogwNII5rnNsIGnlPxtnDhAcGNodh1CtLWI+WhU/ln9AieSUoWyVyfC+ywO3GTe181dOdzlcr48Afdrrmv1thrMLanxL/t+7nLW6kUWw/u1L+dVeBcx6CpM59FXtnhvTudjLqlr1yz4vw1XmBhYr+ie5TBEvqNL2oryJ6zK5oUlnBhxKa1x2jwi9kj7q1EqA98fSvVXLSLiwRG3ibLaXn+JwyLT0+2Y9YHZ85TGfutM1SKAyirWSc4vcXLxCuj9xRqLIsdZvMVu+x2mK9eFOZNoy51PDlxMhoMqGTY6hKraBv/UqNv8SMUaVjkIBgrya7jzm/hKk49vTxs9fSkFPsY/MzkzPPnoElrzTQ8NJVPcEi7g6WUeljej/sX98JUfsvZj77bpW/frpOanT8uvDB+zB3efxSHbBQOXdlIcPyuc0rNHAGZkfi2aj5Q5yPsOPpt+n2sGLMucBQxp5+f4oz85FjOA/5nR2JdJ0VWtRtV6FcDpcz6Xm+ffdzD0YsD+NMPN0VbW/1wJ3Vx+EE1mQ8KyLFka5A00D8SoM+sVLef/1ZES0RX+zqAmrWzJanLMGxiKuOFF3XBLNWyhKvc3E+EkHfzV2WH+EWPPe3e7KmE7C4S5m/P+/gJOdCNmpl6wRVtGH4TCYtSJxd778oPFiH3dGewp39vVSnOmaaKp7yvqTtmMt+/ITuvcJBwo+0MjQhnNXPJnzAxX/ansQiiKzKNFf8m5Qrz9M86bAGejUyVoxLV1YmupWSLgYJKHW7LPbDT7rOdeU6QnNrxbXXUeXQbl2A44uXAgn1tb+CVP1kNYyK2/nlsiaZInl/hge5l1KDA/EjPm/XESzNqWiGxObPeLReO/kvw52X/V8ZRda6ngiT3mMiWLBYMf831cjQaErBM9+fSTWYpIUJ7DoOzDz9nTYx3JBxXlZNexhKzBfd99ciNaDTZVRcPSff+poOfrCpboi1PBfivNl3TYokfTUmKdM8/KfIgJcuz1PmcvuIVyJ4lzbBJPSYN2Ix39AGTyzPCpNt/nNn2rv4KAMaSy6RVIvMooPOVLgBKeWJMmTcn3hdMN8hgC4uv62/Ru7PERPMk22xZNIvNmtbCFwfQNVQ3X64ZiU7L4OZCDWhZ3zMhwGxMPPXCAdTgKMi/E9eiYP7j1ZejtY70EwHFivpf3X/gABK/XRhQhd1jCq1t0R8Jm7G0hilgFvATM824ek2USiiLmm6spMEsZUJM7L+VkIfgJ9riFobPswOsvJkpGhvHpWixH3NNF0WuwB8GQlVAJoPHA3+9Kh1DBRBI4GwL6/XYu0X2bBygNC5oi+C0otJSK1da7G/6zFA9G7D6vGp3WpZcM99fvuFawtup3LH/B3qaBOQbf35+fq95v7S7L0ev2sBxUUSC7MEsk6Rq+pGe51xPMZuFRUqkL3JMcPtHgkz9hDxA34/JA1LwRJT02S28pHz4ltdjsXzoMnvc065gp7gmw1sj1KJuO7gHANIM9Ao5gNdLMXvM1XwbiGOKJYqioqCAl7CW96/ZvNFN28rt+dZ4vL6WwkqMrJS/zomnciamE2b53M692wPYkZP4sWMaxJ4249VYo2UqzCwXqFfpE+NpVroXY5YU8vaUR+pleQo3xZk1frt5S45Uyo+NRDV9gJJ0oIE+a+po017T/NrozFDuOpjNSILjKI0KePfBOMCok6nBN0yElmT1OXVnt/dUg4gGHDULOxkzn7G/jWQKCJqSAFGabXyL2biXOTtk2TqJnXgqiZDw1jilVHzYsvNuI0ugOcGAOa0R2rEXjHgyS1YHazeOEG6MtbI7KbdXzpw7fk77USfUgC1slydwnHyKHGiEwFr98gnDhsedMhpqOzALDVjerOTdEJbFNJPOlB1XiVfsDQvGTOR5PpQul5FfPrT3+DXRnMjurOEwphgzRs4vVSnuPFL8iEgtnyqoCgdY0Z+2bExbXSarGsW3MFP95HUlY9KlKshAcFUp7REnYRiBHPadGxHVPFKqM8oEuSMLsiQOvytfW3PgAOycNxOuRuaOzMyNTBu/oxJDkGjH9h+LgbV+CXOKGGpwpfpPMsluLGNilY+kx8jvxOOfGbq5r/R0TrK/WNLvHQ0/LuQTPPiM4SHwHZfmUe16zHnytPK55hBYvA8HCJ4y3moXLGr9OfyhYyk2u1RHOtFksTEqgHsyrLhh4J8neDL5JqZVpvDXQWKxWqqNfJGkbhJZ+u8w2yypIZ51iKw6zzPlxdSevx91AvFNxxdif9oBfRQfNjcM81jN35t4vxsIGf493sta32zL1WJQ59Lyeq15e/7qe2WsQ81TwaWfWVz5tnTsE87Wy94LPjrc/6R0mIqmwosoCh8yOZWyUvkwFc9FrSbd5cnk6I5ncgwE840Os9OM51X90kn/+smWqsS4UteICn6ejrln9gSOns+M7Tsa2/LEruZWgJMq9ooHf9YLbRgbnHzH3h6QFAVZ3/Frva1YAT1lavU0ZGLM8y8VcGqN9wv1AvK0S5rCVg9m5I38iS6omV87amXW48XYB2e+4e5s9whsj4PYnM1dKOj0avpUhR08YNchU8nQb8DOTAiSkwa4nfWA2iQrSX2IF41WJ3OHbZoiDGI2xe8nqcACzELGQSOVPvRniqWzJqgBzbh3fMBeRIFGkjk4iDkRo1ha9aHQtqtCxhVTc16ZSLLbMGdRyFtVfLbdUkBser7/AzNL0JI6PV4p+b2fxsDWfJ/Z8yh2w92vx2usvBkFXpv6PDFold+hrHhl0myuqNY0Jmyaw7pfrvwIs5BTrLlqc8kGrLQtGvq5q+peFGXz7E5E2LTSN7UymkDtRm+21NtNW23cHQ8C/DoTKSsXwO8zezNlPh41BRpCFVbDzZInHnmxqrwoKPr1X/0PsgJIsUysSscgttZotGKY43+zsd5IzoYcdIEhb2xT6X0RZ+VKz0/IogqjaoDOWUF5h13toDeaSPOM2KOpac3Xnad0IB/6sCtD6DZ34peXX3Lk9D+ykJ3bC/B/TgCfjBIgjbDcHU45ZnCaQV4Ed/gR213QH5V3ClUybf4riSiRGD+REl05sDRnfzlefRmSiQPYx4+/vsG7MXyycgAa8W1tGn6e6pWK+Xsm7Bys3fRauQilsxhGTPspi0ASGiy4dY5xFOvfsWDO7CHoZ9X0iB8En1OYTUqw5QvDXAjsteZ3lySdWocK1caQTreFo8HZn1ENBKvm8HCdgLrbeMdtMNRJsH4/ZlGfjIJzpQm9Fzn+0jyYyQZa2r0cU32l9GelMlsx73an0bC0rKCAlY9NC6A9q6iy3qPO/iNQTMJFMevmjPOrqw1gq8Gxu0cDsM0taT/gNeOhKhh+ZBFSkTA0i2+bBVEInvDDM/r9ThoCiW+QFz9SMtJVJVKuE7SxIamnKsKD5DPeBo0PeBMhhcd3f8YhXnYn/5XSk23+We56pEm8/e+X62aJ2bpWkI5nUCULc0W9iLXgRaaI0XAINSwJByBauXhZmZbygpF0duSWtRVEPtCo0Qw8H5x+VrIoXGisTKs19nO1WY7kgOk7hUUHjUpgri0bknW8kqM16bWOrrTT7/qJKdobL7MQWIxbwo9UR9FUs5JdS+CLS3z0ibkomt3E3/3B+gNN8GtDZ3EN5Z/hTXWD3TXaDAbSZWiTnpgtwV3fmsTLYqqBIae3/IcNky54FjXXbY3jOUlV+56hLPEFDfevkuV9f/U80WgYQZ9abpg9bK+QLyF8pmjAPXvND0dNywGj6yaK5t5Nn1yXUpY/XFkHPHaQL4Kzz4ls1Z/xzuOXlPHPUB8YOEspFtQ3PXEU6QfPuXMrByv++Plm0hnv6rsBRECYR7ilR0Jf/CfFJYbrDFWoupTv9nJdxyP51Z62NDY+kDDR8Fc0bKduXhbtodJraOuzVLBkTJyMMoBGgzyg2/x2389ph/kxR3cKr/Z5DMUmGDrbQJVdtBLW7eDfF+fn/k/zppJ57hXap8xo4zg7/gdeVaJPA0voS9C/CpSL1AgQZcs/cdC/nFKDTdN5eo+ncDFdGKR295C/sgJc0wjLjRoHyYzVPyRHJfcv99q0NXtNVj13Q0dNqk2F/RlnVVIaOAy2ljYvK6oJeP8Es/bCfrvl6WS/JLLULLROLeBGz0PMYOCY1lomGzEYp4yUWfu0y6qY3BR2Dk0qLGYVfMikuKM0S7eW/EZJmtRhtvFG+mNKZ82QvekTKklzmL+Cr19FuXNMeLRc6BW1D5A4fjLBDrPp7qhZJyKoS7irP9RU4GD04cTUIJrdUVTsg1mwRFJ8xH5i4GzdJEtq2Au0fnmNyRxlZseVpNG9wCSe7AZbELm1jXsx6178H3Iyx1Z3l42Zd1EyNtv70IuKbXoxtN5gXifFQNj0BGRYU2fDiSFQrf8Vn3UqoG7wDw6g0i5cJ9+0Z0QfHOpyHvORPz3tjNMGn+B5I3uK5JvgvsKksMYN1wvVD+8ijAz4ivDfaYhkT72c+9XcNgh1THlLVuwtAnGe5q9IavpbzL4UFbzjqp+Mry8adVj1WcjYlKU/q30H2OkH81cltLwqB9mxmiv9fvT+cdHjgnRB4aIvegeGfCvYHv2WpmRj/HBnbxxAyqAq0g3qH/78lnot8ZXDYDIlnal0x48vIO4xhRtBGbuWmTOM8xvI7z7XilIRuuSb8uSzUIKSmym96NYrtda01sBElXNLOnsJ84REwTnNFnkbMQokb+s053K7+9TrAR+wm4srsWQT8JXunvaA3Uf7Yh8vh3cdrMfl71aHm3883+C9OnTGAco5UTfTIG5FP1fNB+xMrfRLCJ9X+5rUppYO/tbQ8Pjm3rw4JZnI7JAHcmukIkudOgmbnTlsupZ1xr+2M2/H8t7+LC1Mr3NtTlbtNKm4pFE9S/ZyXAwxrKkuvMuDcqVGpmblqx8ZjKw5zHxMrkO3hdvGln5cF67JX1iqnIPx/ZOd+UJHBDeH10kXjslsL1nr4nKa1azGU5KPelcjCc6hUxY53FJsH4dRyMfXwgW01iVFkwldhzIx6v/i/yV1F8SNvXlApf1fYuRmvZTPhdc7eNru7RobB/8p1nq2rcqsiDnlxwHuVatNHj6V9DMQuw6cTjZLb50qNHiQft9h5nHFuo0i9suL5xpweb/Xo+cvkKmZafQBI1dFbpmwk01ilOGz1e/jSAuJ+KOhh7mJJWbZFzxXimvL/VX+tcdlHPnBv5nisbuM/Gizmop4nW17S9Kt1OKe3yB87Hd5dO1mtGpm9i+TBo+p1L4q1L893RbJ+UE+OKbBDdvu5j8uEqnyGt7PXkCS+KEpr/v3NVHPKKsTr4R4FsarKYM9lLWFoTvErtPQg4egud/sExknMOh6ilRUaEg8JT4hVuO3NlL6tZKvnPVque495C188wNqs6VazHV+oyFkRGXrfGfoMu1D1Ztcn6UsR+fqtdgt3wZ2gZaEDdqQMfTLxePHg6KvzeaLBykrfikJVMURguTMaLeHBdvrpLNfFr4w2UhvznAdO/2xz/0ynY7zLF/lABsRrYvfIFP/d3BpS79CYfxBiXq3vGAadYZXcM2Fs652k0VP1tKDI/05tF2l17REGUBhdyDEQfs6cE7IVNBHR/JrCy9a34ZjxMNMSIbjswbdkOM8KmYRtayix95CVQZF7E5pemgI4k2Ge+1VvO08Gm8o+L6yCZ3lP8tS9w6bOCsb38UzZGiq8jwzNErO8lPpyjNfHK8S8+31SRGtbx3jCO8b9oyEtb/3j0prCvd8zUrcLaU0LeGUEnrqdQ0pX+MiyKKxTCPQnmpXcd+AWo+USw5var2HspYP7g5BdJBCPeLbDgWm91a/3RNjPiehiEvsgcjCl6g+a5aUPS38PP+JEI7Urey7HzIsLajvO5YQpMWrOhCKzCnNs3DYC11xT8benwQIiAu/iG/kfjEgcu8MkRoXWodnv9TqY/TnEge40HPxn1m1vgEnW6T5HUe88ObK8VEeLmVUQ82U470v+oZ/5MvmIby+93ydNO06wmFG/q/7CrUZoF+BALZqftQlQrwW+z0SXZtACGMfuaiiUW1wWtQZXrQWyHz+jqi9z5loD+3jniHzHLEVdyhgKURIID4T0xYqXhad5sLqlUx9KwRFxcXw79PgANUmFoQ4QEo8tPGKpckN/XUZaWxLxyLAXtI7yyiDd1v4nxa5xP/8cQCNBd/M903RmrfqT97rZx+Hnorz0FgLctESU5IEpWheQC1Cxk6vCqj9Dxct3T9QOY3csjkAvwuZfwwbWdXMh+k0idH9+bsStpS4iAOMvOqLf+3upUESwk38xgR0CF7XxNa/OD25MgPP3909OIGrOFjvQKj/6PSCYt6H+BEl0CRvzMGckj5SxiYoTkvp/oIXQMpShvD71lt7LDfcH4u+ys8P4wuoqahk9Fj4TYIDVFzX3Amg5PG6lTE3pbSlrQHyqh0a27U2V7hFqIWnNE/2mVH/COd3jVDXACEcoG6o1fdaxjJDsrlbTmf7UXFz3RDJPORpk57FQ1StJtMuNSTI81Ezz05UWWX2OINn1PAP/gVlKJxL89p+/SZVUdDkaT2fMOa2xLDDBbYwjwNMlUvoVfmwDj1/FF8LP6448cQBziau9Yck7Jx+iZ7Ht4ZwPZ/n2ncIiG3w9pvr8JBMlPm2mTIjKY54uJ+rUo0DPNGvotpUuL8+0K3rsPAQs0ogvmfSvz0kwuAMWeFHWD1WZC8huDGYzN4hAvfaiiE8X/seoOXwzdad9eeMPxJMxCT1nzZsBVNcKUKnEmwfMf05oV4oKbsZCiuLe+j/jf8mCQGbm37pP/WSrAYfeMPkweOuKPag5FZ2vg8fpGK278rFVG7pqDFGWx/CryMNf69nwx73MYKd3qantHymJHNp2H7yNfNChanXzP5eLk/MSzKf59DGeH3a78i+7S7Pwo67PjqVBYYryxcdgwzsGKi2HL2HjMaMHNL9JArBlfMbstiTXSfJ/XHp2/mDzofcnbdNlSXnLqrmCfITvGFGM5xHNsn/WPM8wWkUHat8PcLlRZVsan9OrgJGrtda1In+mVu/y+isZeNeoOM7d8iDQmChLJpWAmCQSvev44sFLEekfEt8fubhU3FDoEdg6t0quLox/InK7dppIZivMCUrSmtvEOtZfhFXvdYabiMxTKnt5LmqrizY969tt0SvCLr+kS2nM85gK5aldhTtUeIg4axKXUdMEU3zIyTMne7CGSte2W4qFy/DJ5zt+I6GJknFEOg3yK2EUbdBjXSa9EDLnegxXx/5OVF3pQr+5f4NZ74ECti50+r4E3yG7JqanWGyDBW1V19RmplXmB5Zk9rLEa5LqmV/CDgEHOx6OrXVnxD/dvWsXEha6wiYqIaIxOyyeiBwAG3zfc9ntfUtEchBZcQvooVCsE87DtBTtXP4QkNVburjCbEQuDXmNabWn7Vs3h/CkLRqnLxmlcJGkQbK0ww8xQEOuPoYt2R+xFgvdPruXZZwULJgFn6p6NypRu+VuMDS+/QaL+oNBy9NQyzFBj9HjlfDSxQWjYhOlII1jgd/jdjcd0lcHHh6/Nu6Q5SpEjsiM1uJv1aeyTZ7f8gV/WF6k3nW7FTmW3Nw7GV58z7rriD6bcYBVy4s3v8jjPxC1S5dPDFDgHQwH/9AGwfgfXJ7coMDUG61y73qwsjfX35JQBGNN2euDd6CDgz0BFxH8iww6tS+yr6qrlNMbCMbRXgsz/e615INt70I1m4xJkyfombWaZKxDs474KcbdJlFeIyFO80Ga0Wvf8wdV5qlekj24trs3KD3D0F85ZWp0H5YzqX0d4lGOY2hgIOMLnURBX2fFMErJZ+/hthVpqzryyEXOaT0c/N811+mYg80XQt3pSXGf10nI7TN1lB5qklcqttRPgswkPbyKYbb6OJW3Pd79Y/3A00fEOuBFzvy373YAmP66KPZuE8akTrPfyx3Fcr0pH1HpAqVlDkEMpS9RnP7ZNLafk4ZU1/qKIjf232Bh9BxpfqodW9MGSLwAs++UOh//g2j+78esiDXGX/xp/jHPQj8XgaLPvFt/RdW5R/qM5vBmkEZFBHXAYvYQ/EqoAqlaqmqx2++oTa7fNA/0FFBfekaQzLr4NALYyOSe6G7ebv+FZKqkY2NHfwZQZnkvC1RM9zHC4c9Ekn+2IOnbta5ReOB3wOLDkLKxBoHcvbcXAlOvOpC7fJ6fnewDTfSX1SFOfqZGnPPceFXZ1zNYMwa13kMesZxAFXEvisWzpBlbKAVL/HJODDUcrw5oOLo4zSfa5VW5uxlfoDWk1xV5qBsiAYvm9iQSXdrVty7mh9zHo0y/wprm4Ike6usOYw1Wfws1n4mKiHYQezuQLd6ORygeyLvHSKJ0oUY3MoqeirMRb5Q7eWl2WbPN3Ur20G+4HN6ik/mzExr8C0wPPL7maW/u+wd+Q50ETh1evbs4sXjZcT00xuNwqUe8O0WaKo4XjjLI2paS/PKz6p+eU2WPjXy3/Ci8CKvv6l0CPjwJcP1Zrp6kAbo9KiaMghTK4geb4I17pX/DRpBURljv5WWO/aGfrS7DHLD1ssVq2Py/sxalV2hh0t2b5zDyGiiPQ6kW8H7aRaKx/vxmTYnAvgIgXkYts8otsoysR26xdTFDlapf1zPBRT+Grl9l06jiwfUQ/L+UtVQcxTjAIIKLsBOnR+zlbvEOIC584dg8DKHui6YeNu50y7GGcBWMWe2C1YmLEUixmpgiq0+d5JSarIIcR4ulqGIoLqFf9bZ0ry2XIjdLJ2sbs/cWQ25XwVa5R2/eoxUb8IBkGnc/m7qauwyL0cTJOsrtsHSF47qdp0eZLnDByAAuFIe07yaonQrvQKvEsfY+3DhADy3EVDtkOKrqGDJR7e5PMdba6fVF0KvIj7a9vvnddrNH+jg4QA/Rn0SSawx+r1oAtQEuL6NL7ByBHPKLV4K5rmNvawPqm4zlmKQ2u7EUgJJXstAYskw6eVAvAUFP1LrTmeaaQMxHGDM5/0uMzXor3toMi9/dTAfeCO+DwdoUDWAajaudO1qttz+Z3Mt8rjzb9Gfj4g6rSoqJsgntpf+UlBnhBdKwKnnrQ+TyNvyOiusYLJxD7KToTb9SfoFRQ/p6wVUSItDaiNCHgfomvRSvFGL1LGwBKPvzaBchPJE51w6vlxyk3Uy9Igrv4dD51lBCH2R5uO1xCzVvGMj8L8C0SV6JqHWO/LgnF8wBj7uuvWbPxFiWLUtfTYYJOn+uwt8GUjwT9qj1jrhraSVkiZ2xHjPZ3VLymEaeNUFRmqceVP01jQzrxriADEFo9gkTOsBqmAMpblGjQNkBJxhd4GY3Hxw+BKrPg6QaBqHA0xTYOgLbzWiyMgtEvOBaHMxy53370mVwPO6/3GDOkms9eVR4zrBakMbFCvNhwMc0+bt6Zj6Ext/2RS3nXAreufDIf+bdAaUSDVywPB43DEMuwTEAWKLbn3CnrRs6QIv/3PajkbxZVDsHqk3OqFRG3bSPpX1PLslZM1UqcNU5SWtRt+EKxqZ3OOR19NsjCYoUfdi+1u0e5LJzsFmKlsjHeEBnypU3WNCm+0WYudh/9nGzIv9PlAb4COemq/oy4J1iXHkP3xVERCqMJxVPIfSsWtWjNmz1NIZ71WrxeQkMn8chL1gqz1DXW5dXK82pjDcjYRSkN/CadhVsWTmyPUhV6dJzNzijwlenX6ZUzLYjTvMoiMt2nOexJkqpfg7ycU/eo1Fkg39PkdbxyLinRxNyTdXe6bpLh5M6wKzDQN7DgZOvtgT3SvwyEUFqd7DDr8+9vD7zIWQWSlKpRXg2TnUU+S3omZQvuIa3QZC6MVYlS0vR0/S+Euvv8820O0LEk/74Pft4jZrbI7domzukxLrkEgc1oO3i/S/TvJC5enTsswEzpui/6Se9GL1Cx83OoY9Ale8lSBb4r9jTiITIvpBleCqTXyUpFkixja65AWwy3kTB1jjzl6iR2jZVPIVMlc6iMjkebYaXZyg6S9/wQzBWL5i7GwyDrDpODmxJ9R5TW9xdOE5qY8xWmEbrf7eeHNHSPlEbZfcsKxFIUSnL9p6vrxv7ll1kgGdEx2l6jYNW5+Eljw6dH3OdtFbWjQp/CAO3G3uDZoXVNE8w36rpmxGw16dSU3sU5IuBxE1i8fjAGUIUttm0k0FmuwjKx7EhDlCG7zunYF90IYDCAuJRterxflPye3XgC9bLLYucAAS5omb0dPYkBeLwUuBhI2MLSL7HhP46PMSPh2GgLi3H+O/8W2ky1sxwGTjbNuD/VtNZOFxyjdzpTjAnN4q0sVBER0fFdrAc0dPduak+y5LTlXlaL6tLMxHcEKzufU+Na8Wss3+rdaVEb/jNbFd2qI1E9/u+ImEG/q54fr6noEi5kAYjIqRzjZWJU/efIvI/c/ud17jCet4voRrK7roX/hVmirncmvzDTjA94asvBBpECrm3cnTYp4HsboTxEFG8hiDbAf4jxzvMfiLGCffeIhQxtDCI3exsvGdyIyHT0H7wzCkxWdMdRUxHW9CsRVFJ0mWkaeonUxuR5r+RfkMzdVcQipq5/jJDa8pdCE8KvI8c2t55opt017Z+dyYHHkBBVtbJHk4cekuuOAA9IewVc7U/Lax+b1ixbuQM5HRTQLaaIhNvH3AidK75Vg+ka9QAxUNk90Sa8/n1ajp5cKwZVlYiiGl4wYa9oQ/RAc4wConJ6qODXv5LU0qcOkO1DzKZrrqQRwL1nQn6K4D2YuoO5dZjQz3cSYIETkwrFLBgzR++LH7yrdiyquMBC/86ubW0OTmXLKp9rj3fBn6DAeYLTW0jFZ4AA2HEd8H3koTQe4c9C4gqm3SKLeGu3LeCtZ3ndbM8J/eUy73zZDIzSi4yyt1OgOu4wwRp//QKQIH3P0atO/JplqeVKcRuDRGPATv9IFRLV/3TsGk0PDTx4o3lOBo6MAm8xIPuC/NGnFo2U2+5zfaE9fQoaS1qhLfqqBZ6V1wCKSY76N7DHElmK9av7ZOeC37URettuzHfF1hdNHax+DSFvjwBM3vMJaqtUu5R99VM2+h6lOqSrtIHV8nq0d25GxB5flwc8U2fxXJ5cWPceFluyZfduy5MmqfzvIUSmxhJRssI6DFAeCKK05fTGOjbV5m6LKJ4O8nIfERflWbIEJUyqZpyVGFwYLAC/FgOK3+gmjtFj7z12lOj59gO0fPnRRzE+lOlV+PcjKtdALTJT35F5A7pibzjOgJW/HkD4iNd4vrKn5sr/8uHpk/jS1lf3AABTWl5vf4ik6MN5cP+On7G5uIs4F8IghZoQ1ZwdzDoa4J0ru6iEw/yWUOumesh5x27AIAP8URSzlV4fiDOoo+1mQSmHs0HgFzR1rearyvtMQlqN503mz+NXefB7l7R5zgBPUSj79ncNMENf7jGrUVg7HY9B6pk3Mx6OfNxH63HNpTUWsZHMAkQXzziRBvcnadsWTjq+nWx9j2oGm/S8vHSmIRKyF8iSgd1UKU544ITWv4KR274OHMYtZPf0yg1o7qL66qLVI/pvbFcrhwg9196fYFjQGO1oS9ma18ggYeSJO1C4+k4oYqQ8A4b8vBKRkaLYvtw7LvoOFlO+n00gdflKW71w3x+TVpT3sT9CWNQ4/UvijWUAvlPjk+WDge4T2YTSFYZrgfr3ITtkvmHohoEdiOt7ZslQqL6qWb3SCTEpK6foMDDPgr+s+jCovF4tJ6ZUlsoqJcjZCuwV0ER29nrwtBftmG5TjAP9jxWsDDcaySfDs8j9C/0XlkSYPwmiG7urkkY7UnPSrWrfRNPPVIHjFtEbMWKJBFFFzuplGY6xAkzhcRUxGUazLeXz5wnx9+Bh54U5OLA5yPP4GXc4gtm7Gqttd86rC94qMCtjYltgMLEzPB3OcIlJ09PqFbxWglPMf1zbcA4jzIs9SzZ1frgRMj//YEUjDpN0uU7GfOPVse94CwRyPL8bB70tvrIRFlfFsZQwEeqR0Kb4ueCvRdMdT4WsBRNpbvJ2ly3OP2OdKCG+CDvlS+27TnCtJZh2J7Q4F1OADhPg4QdMlkpGDdOVtR3vYOevQHI9ozu3JsOIoQBRJ8wUD3TSpALEDrJ/F/erw6lnQTM2UOpxgT/HdUk9OGW3PtnpaWzte9ZSi1mhuMEdArB7Z9tw53vWXYAP1TcFKB90hgoOmsHSn6BpJyT9+HGOZ9R95CtywK3avGt1YfLGgvhqTqNDa9m7/0bhY7szoiKQL7xVePjBKV+xwnmkYfDtX9Wiz7yh+RxNWSmHpHhVoF3rsEr1x9GI8VerTQXhCs4DRKsWG/Nd86wOnuc6GA5cAoiFdVjfQEDdO/E97KABFLyQOaTgtVi6On3nm7J0rkIS1ClafjEqjhvqx1lWi6tbR0pec1lANPCXOYDMQR5zZ9KzelPTLf852aKT0T/wW+C+WMjxykOSuNjHIZ0VIcKx827AzlCOO85fvfqDjLsCbfsI1PDBQFDFB60iWh0jWLLumGPyBd0s1ABGQCoxtGd0iORnKEMBjd0t3N6p3vp/f9tmPHHc/9XNd9nb/zqTVzdFk5JhmFjTMKAvsWmKxO9ZljOdbJHXiLzr4f3y30Tib3+dXUzXfpyCy69aDH+9XlC7VnG3PzjMCl8FCQQlHTr6ValSJcCEE69EU/7hJXS5VyAHLC8ADnoJLKsgWn66dvRP7+Kek6Eql8rWz5OV0BMW+WR7N+BDw+ZmQIs1Nf0+HbJUEUdpUuAdutl45eaONkKmWL5WSMZ5cDqmhOrFs+vOsZkDCvjalS3YVM1k1pAkybQ5B5petw7CXDGGbrK01ZyhZBJ3+RUf8WQUpoWunBJemAvQ2uK4q16ncuJ1fH95t/ntP+LoozyfyqqGtDk/6x1GDjBcYHtS6wsed5vOMs52WqY54sUikkdpH01NFX8kOnceDzxZSbNTxAYduN3tCot13I2pqiOUOLYlxU313e9P8+bClnY51FcipfS7PpnqEo76VP28gSggQQKFT1qHx3mNn2pP253EcFjF8R4gasb92bt58dZFGGFGqlWHFipTFCvgT8gt6pF7ei06L3NG5rmKhkfPH0Fb/ou+yqBmiLihhmptD6R7t1lOxwz6zcxcI//1E08S22tui0f3BAET4RpXpatOk3RHeiI9doVW7cuWi+fIEH3ClupPIn12+axbzjWpg2kOtK8hobNM+cPw7ahvTcfa/uC8cDTG40nw42/HfanOlDIgpz5onKszNm4JLo8Gk0PKZZlcqwodUeAX9bWZbNhhauG06GZC1dpazZeSeietmmxxLmhxc6IyDbxF3W/MJ2Seutn2wgtq4m1ir8O0kr4mhVGWam847LiLEQXBwcNMtBPtremQMijfZf8Dny/+8j1qb9qDwZ/MdnFXh+0I7R0i+VWhPRsAgqssn7a/vxvHh03/BpE8SBoRyCBJGx0gtut9NaEPivGLRsaOgxpbpqC7oqAetGt6aTkgvN0ZlsSoYqK1SFS+13wZf12JcnDqSMHFQnp/CA6gJgmE+Sg+U81kEVD6BUnFMdvLmO1AgzQeJutaX6dWNqCLDh/y9vU9wIQLTc8hsPqAwElbsCjyoFTS/dDfh671EsXb2r69kungYvwYvcbaVKD/CAb9a58vawJTwAsBOVVgRGjki2T4XiasEWtsFXyehDk+OKz1fkJk7X/mMGuy1gBdMj0I+xg6ECPGAJAUTz8NlpDP4bRKvYG0vwHmSNtRka9Gm4O6T82/opm/1IzF1ll9xOBk4lB1/yzvUw3OD7I8TPsVwDWP4u+bZiZmHSAiHA4KYD3GmhmExWwHkJfJK1QOqnaxwe8PSq7xwtBg5xDX5/nOr2BcM3BJyREjIOcOrEAwhLU5zV3GvbxJnagv7gztyA0zWw69BPsljfyit1sKmSKK4PisPoSM16Rv64jtXGA+DLOAHkHpIKeu2ejP7ZQfBOGlrsM/5ITPcE3wbYR4zvStbCsYnO4Rw+xHjUFQfdozoBb4dTIv3Dek1OD32h730J0KROq0oFbbUpAqJ9iQlAVHIRu/O/C8jUdXM6lLk+2uiC7f1XOEMTvSW6m/fsXIZAf5uRhZAmoYwiOLaeYNhqNKTbwx9votnVb4L/vQq37xfdqOPhZjIdng7+4rr1XPU4u/bOsAqUCXsn+GaSOG3lCxWarDZ3Jg1jE3rYzXyovwuOQ13AFqQ5ENewv27EH5TAfULOZ3xq9E/njy9EEZhHk7fGBQMD7Bz+g3mtFeW3ji9hLTKLAn7J2ZRkrHxfnVXaCg0ht3YMGy0mC3Kc+aNjkowHkKznjRdGgn0pb8gvsqJJ5Nx/ehv8ByPHjfaop4Pjk14sZIgeYRu24B9PCG0L/Zev/RJ8GbmNZJaYFKS0ib+JHG7rde5YSMitjpTSwND6uOdPEJ5M93a8sOJjm8Fo0I94o3NwUIL5cquJbitaabSDQryKg7Sxd2zszma5O3PXf88aeWuW7tAFJHwjOwuVEU8v0Avvt49LT3VuaoA+oENxZcqROavnJW4VL+ztOZKTdhMvtAAD/72se7RmdcVHhb6Fo/zTX0lrOXPRP7h5kPc97kor/vh5rc4lZxnBSlqKgjqLh+mZlEx5y7ZWj0aopAh5FggO0Vcl7wVtAIuECSbjvDQRD/ie1v1wQjDoHKJ6VCAMEczF/dqxwm7BMNzsbDd8rXhASrWakcl8e9/ucNhjuu2kAWLnZgwX+4ipaU9bAewTKZY7xum57Tu/k8WgQ1oSl6vNz5FC+djZAPCyRqXFZXUSO2w+KqH2viz2DvHkvKZDVtei72/J/fab829SjLYlr7HFX4nbTdYV8YCH5OrsGfqrODQesKvmDeZCT++THf7bYw5C4YTET+oPm1wCogVl3OwCZoMwpnjAXimHn3T7YZny1S+BwhXS1QqyEjwgUA3L1QjTxbGIVOABYZhn77b6MwUJKEwFJRQPBQFNPCDru8l3K4wdN+5ZWqcr9hcCd00oSza7q2mZNxBYmRoMmwh7gzPpztRaOiJMboMHmLFjCCiNB/gJqpLFUYB9joCXMqAMcwKKubrO4oDoU+CVZszVdnDA9X4BQ8gHMKPWC4bSY8KhcEqfgQmH4HA2TeXqMY0HuGn7937TqyEdt8LiQAnv/JyfbJMmn/XbluB4M9LCyyl87ifdTEai9v7sazQ6oe/tgQcVzcC7lYTSloR+egn0uY0HONhCMazC7PndxNtP1cGdyi7g9Vrw5Taos/DSKDngtK9hlhLtJoQHXJ5pEIcJ3gMFLOFwE84rdoEzp8xO5k/xgBBdQsQbIX+nZ8gvAu3xgC3NStV8hI273TELzfMsETY2BFYQOAndU/6HoyJ4wOHO+MceQuGVIFTZQyiuleNYYxOr1XjBAe7N2L7G3bLxDmBSXsZKt+3XfiHsbC1CCI6gtj8JTh0SEMtZyt7jkP5T/ANo0ZlQBDSdVsJ1I+tH+H4ltBcXt0jgAeSnz34etANPXooxlLSfrLPJOkOPi0IqKk2F05wuSvWSHRbo0hTRDN7b6v0r1IbHFHZnLjYvDDvuluda0q0NzKt5nbX/1XSi1yAEqC+vUB0eo9S/0dvyis2hRCpYhPLRYxOlvd4hS3NqOWTaJZmXaVTDmaSrvstu0ptHbI/9PcFikYKl5xJKiGlnTPEpH+j32OxgX8mNTB6t2+SY1XiQFs2iot63gYgiDIPIRfnbsiXYtY8bw/RKdmNrc5NykvBTuQyPdgXJxSRGBZ1xPxqpKqZQZd7toLUnQP3qVCk49bVA87nUaAymhFqwVXrOu9FNZAvGkUezmANevwB3lLQi39B4CsQCnyIuX53zSppblj4QDg99W2giJLpB2JwhZvTmn9nT0JXoG2vc1LgY2NqIID6rqhm8ZZkmzC6kH7XHKgp8h4T2n++FGo3U/teXSwpnjtUhPhrSdXo2n73Ru+yMJdD0seCf/qLFgc/9vm69QmTQzfqtaTcL0b/o8a4eY8bAFWVbPMBJOm5Y5EY4G+c2YcLvNiaMiKAW63iJBwRBjwoLI6PdIwmhr9IN7llk2sbWeEO932K2wct8xyTnE2ymOBQjzk51zhtHdCH7rk3k+39+q8cmx8UaCH4r8TUsKLvC3qvdQNIpHg9odXpCkBJrJ4qdStyvmX7c+XcegrqPaS2Bfxv/2Y1DPI4GeXPgAfVWBJHT1kE8hl17m+JO+HEJBN3rlHYJwGbGEo7D5hceIE0BdlzDzKpAli5WXuAB720DZi5f1EiSgeg+gNYPQAjPK83jq1kJP3g9DhbQMoe2fHZZa8SHI4qtPPFR3Td4e1mraHJ1t3uQkJKpkg3X1DvOV38INA/tI68crnOQMGFetR/ZPxwNJ+z60j5QrcDYlCwBXTxu3mM6cvd9NMCDkTvgZo9IzGrubEX2ANKW4ZV9ZJuxv16Vtk5PstpJHwIbwg5K8PoPpiAJqs0FHXQvLStu2GAc2ptMLvdv4dTBCpJ5Ju8rvviWXOXT819pbA0v/eWKPCg09XpktrH7x7j0WRmhJgX2UZmfVNLomd5+UFLEsMsFfmmz78rNF3fR7P1ClDoAfLw+xOt1ARRozgwutYnVm1X0ANUcjN7bgBhJ/hfHMETL41K92LvXrc/C4nzy1hwULghhi781HBBBxul3QXwVNqGsaJfNU2/3MAYeuTScyibrKKWxI1JW0EiFngZFEv0nu0T0M+ytzI7x0K3rL/b+ttoTzDHBymTAQtizfWccmKbnhVpIZ3H/gTJjUx9BlHgNLSd7exYGdzzarQyyDsJcXhhV+Ce7YaTdMu+PG77Jg3FzdtxrwQOGbgUNS2WUVh11t9s2RxwS+f09ECE/l2o7SxlT8RsyvBjUWSJJrdJr+vK959cqd0dHXzlX3+7/v/tTIB6iDygsEtHVb/HtFWa+DAZ5rZ5stPIZjD/hWbIjktU/dnqy6F+ylQPTrwhjtbHVrk7592Unuvv7A9DL5PsIXITtAIjLPGuLazkasXyd/sh7iqTx/H4+dGdQ74R/9la/6F9teUcr9mqatetgYhZOp22coMyNE++szNacB3S4vFuLPqX3rwji+mbMwaE3t9Km/p1fnGGxM65PFFRgMx03fkYq6lZO0tv3SMKZnP+mcR26oWz7OEuDYpNnd4hRdC3VSM5xz2hmXzFO7q4Iv/H40+/9+X2Hcgazce785jUwW1JhAccCFg6ps+8ox9yvh3LmcN/Uz4tnC+NWAoD9ccezvFl/awkagNG4ZbIBRUoWb7/Xee55UQ+v//ZdxDdJThdJLonR1FeBScGKIUWu2yqkkFtvlMhtP3CQFaTfk7GuQziDxJTSLzHbvanvz3L6eDnYa/hB+vnFNkI0dTUfwQ50ffMWodT+Xe73yk/uUq2iApVO/GUV4z5NsP3yfCPDfyy60+djtVR1ea/Ur+fmrCIXASEr/OL6zeEYlpu6LiO7eB0qNiagsjZA1AWgC1gm33ireei3raQ9uSRwSVb18pL937cQtAE6ocztVOHEODGuyZDHcb36b6TIZlLwABZzLOd06Y7nIvBoAhpW/lyEWadpDr0bK+XheCUZVme/3t6ylPFSlChDw5ytexONOM3lwZ5ejxiSOOIBKhyUCPBv6Kbc7yf9yKnUd/KHirUrP28BE8NKignbaYTHzBxX8ZYA/JQvDSEq7wu/cEegSeGYozActpxxbJ/cwMD1PFz1rNiTv9BxXlL5+cdmLqE0M59pfVjZQxwl8EIoeXNj7JXq5AyoszK660qZDdyf/0W8OuyCgUDt75qBmLsEgsp4KHeYT9DYv2/AIdYbwUM0d2dSsEG5wOvv//4kYP3rFuEchibpMOyVyVG5+ms5n88vLN96mbwHnRITalA7E+Ek3IeFhW/KViOxruUVG0HvXN8+vgJ17U/J1OABbaCbs7G/7WSrGUxTR49A5U63IW+VRFOQsDtXnrgg/gAHnCD1kWyYKqYzl9CY4H1XSvNWKboIY6QTdJ+2izB6tD7uaf8/H6Aa5CdOOPA98Jw3wYttc2SJpvyBERHG8aPFA4hY/pk14kCMBHh9WLVzRfW4Ih71/OF5TscwOn3QDzSiKlcxhh1MwjWWzRFAa5SFZdvz9AEeEMqdqK2DB1h9vU18WjHhbgGPAHfX91riMEhG5IQPQcbLtfml8/SVs0E9lFWCtvfC84/lGbyXD0ltp5JC5QXsNnXVfpHW3PUmvqVIx2f896IirHvx6XjBr2cfiZFW1DbB84x3HFdvX/l+VRWErcDovCAPcqI2sBtR0gPJUwOqzlD99fzjyL017w5ebc7nutryupi/j6mCtqgbSpoUekcjePwH0jpWiaMa82LeXYe8i1pLMpO3vIYqbbZJ1XG3UxW9iYa1Oizqviu9JJypAk4QivhWFkjL9NOn8AVwS3bYDgG08pieXcRghDZx97quywX6v+ay3Z9n6GeTx9zfKHPLpc4S4EaEaFkHvfbQmAAjMOeldy9fcofS/zjUQvQNB+c0YqBM8a8XGr3ML8PMcf7WL9S2sqcO/xuDiByQMlHynETwD2teFItFyXAQgZLds/glbT/cZeaQrHmn6zSC2qzjr7jLtiI2cqexh9dVjfuZCm0rx0MSrywhjtm/X4KuJjyb4BrB7gCptBOCYx0YFN+aJ9V+RvSmWAB28PsK66xWtyIT8GUu6s9x5amtDzRWNduL5vOe2GvMLr+tnOoAM+jiCLaqivaFXX9p/96Ii7dlGDaK5BNFHMOG45Vmhu3e7qOg157IUeiVGjbn7Wlv8XkG8WlhkS+nh2BIl89Y91pUHUTQwG85GZpNiolUgv8SxtTf3nkt3e82u2VL/eCiHEm+JNk6YBWUWdD4JYOcmykGNwg9LhVKqkKISLlYjTQUOvNQE5i5jiJ14ausIKo0lKjFvDPgZaRQYWYYaB9yVkpqyXkjAor8OH+2zMphuGXzoOR4gZmsdpVD4Ba/aH7J3/o9SDodBKBPEAqm2M/BbNUVh49i2hMHAKss42IL2/CQKDvkOZBiyMG6Wc97PsBiyEo751uzULb0REKMU3emQ1uCa5GyC9GhrtnDieRTTOngQcEp3WAjJInEYHvI0QvRXWN4BVIIuwS3tsZMF3WIawbhAdk6zDZvW3PCNp0XoF3AybqIuG9Wz7noaiy2C2xe8ZSNczyp+XX5irApwktiI8Ni8yLWSGSS80LC1/xnwwf2POgOHDn16HQORH5paUSRi5Tz3e25gFGFqy7Uw2OQ45jc61SE1aBzZ+BddyCZ2Z/Z1tHzqMfgwwIQKsaucelgNbM2cCV67VTGVmmGwP2JqUOpUKZvNvMfa/ZlDm0d/YvuRZMtyOx8lAbwrsq9semL2CTJw959oxP66Hrqcc/eCQcoQVz4FzmGUxioH7g0Q94sUE2ozxzUYZu/S07tLj67h4dhPTJF2otL1pL+G02lbTiUcd3XfXPV2SOyVFiJnnqFB9yQTOhJOFuLvHgejB3Ug12j1k+B3GI+xtIupKsNvoYEYHNVNdmZoD5e8WhsusFCnmCtqw90mHFlHv+lq6VP0Ul4Ptj1dpNq8lPG2kofTzQyYzmdd9nS8IDuOm5vnCmBLgqimgWypt5kClQ71tgcSK5mEmZ9rfP3mDIDMQ8Rlkq8jGkkVDsVUvGHCRdCt/L7ShSLddOJY63JscI/gq4rduruGwQqt8QME3ulC29Lp24ph0EVvppxvY3Zl7ExfCVRhWRLcpYcemnRw+k8PXIrSeL04z2Be5JDRCrOqu9ETIARC9N8ZaSEQE/x0JcN5Ic9GCt3N5acdicFOYv7hW3jjiv0DZDxTFYkIkPqisXO3FULdOKu3fJj2FH9zBfEuGc8LJ4mBN2RrtOocw8VJA29fga87CsHkjXEIcRs1KCJxrADQTaIT83Y+Fj4RY6EEJfqKxrtN8xItIDVLGzdd8QMD7D9CfgtzXvoYxoZhFRTzrsTGuch/Sb+861ULbPCKM5agKoCIG3IFSMTuTl1WsDlc1YskTs96iaQ13uAzM4VaDPwoflI66PR9PD1XNC+EveWjYdwBWfh+qFKn45pTbu+o4zNXFi5wGlfscddZ3+blI6sNQ3Xd2RIge8oy+hUgOFoqgP1EIBHsJVTPm8I8O6YeIfrXpD/ax1yfVOKit4yU9vZRzTlaQaKJ88G5Ig5FiK9E4bTpDI8eerGbWtkph1ayRske3xlxKaoV0uf1A+fy/7x/EBIG4Ib3RuvE4xoovvCmTitIvwoAIRr0fBZgVF3Z3gRC4SJilKJltL63JeSZwS7FGJwlJalBN1iQIdp/eesLZZ6h76o/y/KMmLkzptHKv7U7zHFLRswEOmzm6ft+QLY1R7A7aK1b2JP1B+IdGEPpreWFKD5EncsuOajVoKecvYRFxUyJJCUhpG0tyAvVYeuNSbWUjUoPteI7ORuMB8RQ6+eUGrbeziZ/n52uK/kEiYeYCa2Cr++LK3afvH21matMzvaRBTTYLKpYzayR8GZLNlBLzGWQEhCWWC+esgl5QrcSiLpVnoeQAH3g+bjNZvsrg4z6tw3ur3Bi2DtkDK6YduNpSXhzBH24UR8Fmq1Wt9DmhIeHsxrubCo1kNm6GoDnsWqpvomv6f36NgADn8AJ1hLLzdzXPmmwS+eeZuffOb+6p+h6xj9bKuOHWYfiYhXbZwHc/m8vBizVNIniyIjjX+Tfp70BvxWJ3vsVQ4yLl/6PGriK0hhHLpPgJXimiaCH1fanyYf0YzM3zmJBtdUkmfxlmJmI30YRdvKSqoU8kJqvr6O/nAXia5ts/8h1l0+LS/275XE0pLR2iEuAVX4VlKklIv+cu4XduxEAPiJEYNbEOLCIQl7pXpU+jnJlJN9/PSJQFmADc/bfV8gHkD5KYmk4dGx8GgMYkvZxxn6KQCo8MupvAkcwj7tJ8nRZX3juWz/DcbSTAp6O/Qqa8zJich4O9bwt1pKG8K6uj9mv//2/G31fqe/HBvzbg4MC1jBh+LdmH7luiUYqZf+R9hew5OmDXbrPoxWjaoUsErTqWZhqUJ2gGE/Hbz6e9ylrWCkeBD7NrbW6AkkQ/jTEeug2z3in544yWD9DSPjUU/pvxk8SZMLWu1nlIJxldbqc7ktsxQ03x9e5s/R5csWd5YGhB1VOHK6jZDPMOwMhVlbiYMPE1d+6lbaPdzxyO251D75cdDCfod0ay7uuseINDOfdKLMVSrNilY+HXAtgixSM9YX9Ddj/umgXGhyvcn/BZSaHhB/JWEimXqnGZ5JaSxcdGoOTPoDeqI+ZCoimbKjoyNvQ6MUVZT/7dr0Z4BeOS0tTPT9rjE9eEWxNFL7wdAfFz3QE2+HzpsDhrpdhhdNwo+5n8Xp1ZhXRjirjzGjc2By/+5vED9cpYVyjSLrvDbKAyIprE/sr10HYPpn7QwLe/XRli3PdBNlmx0q/pJ1NFTYf6JYSUDK3mKnrk84E/aT55LN3ZJvdil7q3w+/5t8Xcuhau1jr8i2ut1R0diZbnK0OWoU2vy8YA47Tly90fS0Vl0iwrBSaMmFOuqLVAK1i67rkiBL4HOez7dOIbJP32eSeoLIBngzij6i3rtUyJYkrJ4Dy7+Wtc376KgtZ+jTfmj+ZOcipUPmUTZ4fl6QcMZp78PKUaK2+9yxMWkYDtrv1Q2wUwfb6D7p2TOBNPy7jrCWZC758B6kEpttigeAfm3i7uIooMW63eXMfxTI8gC5x6/e5cYaBdagQjlpwhJQgucx9VM8RVcbqCVuywLZ8594QJQwbqA90gWeyT7umBwfbRC8KEVg9N9zsIGfrI2G5ZkJziUz+tmeLjpo5I+kU3NM4i9HjLMNmV+otlS0dDuhEvmRo1pOZG0sFphrY+HFi4ibMfpOqSmuMq/ZoVPwEjPPjRb7DEXx/A6fhJ23c4JcShIubeAP6DCmVtvArilt0wIZS26tpnH9aMLabUhmFasVOUZ++OaV4nUjclsn56gHvfondvixv+JAFx7wXj+fJoIGslD5Zzh1wybKkbcgDtck15ujewmMFTLfS6mI4iMpiZAvmofX3o8BM8Imy/lC3Lpw9Yt6eMBuywFBQm1bIzJXLuKnNOLMmIdPCFajbaD9z7iJNZwKD5ALhL1DQ7eN1vTvftc9Odv9hACzaE3U6R5RyGQONJRc0E/76p7Jpj8wB7kPgpspIv9dtwlVxdQQNPpWHsEn2KG0F2UNK5O7xm/LOawZt/13E6zRf3fqBo0Y4o3Gta0Ok9N7QsuekmMTk8c+tPtYE0pgXQLOrJV9wHRiWt1bPEn8krzC5kS2/fwy7s8N4gYNFdWRfcnyT9XNtGy1VZM2lci1jUFih2yj+46qh/ZZSditeDxAIZc9pHY0NnHfcfGX3PHqOWJbfnRv4CJmp8xlBCkgwo9kMkdH2WLE9veUHjYpRp3wgS5HOigdwSQN/d+ucUlPXsFKlku+N7HlOiFnMOvAHge2VTzAT4h8TVm1Jt2DxjlJo/DX8Z+sO42JWvvo9dOxU3TXeUXoVPdjw16W6XKgt4PJn9s7hQmVHEvhSrLh4M20b1GgvzzQMYGrda+8U2ZL+WelvFph55R86D66pwsMQxSjhjIMD55Ln2uo9gtuaEuxNnx7N/WyxjOTL4aQTUNGmWkrVHxPlIaTJbz7RIix+TiaTIM9K47pmUPFdLVtDIL5NCdP9uHxHSh8Gw84/40HbFk2LPFHi+norBbfaWphFtX88RKxIo85NcymutuwUkxJocvLHK75JYOQ7FkQ1FE26Chlu/GguogQfJrqPOCboFkB4NVWaSrlwKxXmFKjUyNdh2HmgAshpKvjA741UxR/xy7H5GanD8RQZgUb5pepRhsp8tLdIHdGgVlOgGUEikbt3UMVnWlX5X15yD0FaoPijehBOOSHe9ZmK/94dKPkg4IDqdpRBWtSWUy3ZcY333G9a7mCA6aMbsV+kVxn4wguHgRFvCFxCnlVgWUoHYrm3b04AXWGM0BjrkB8PCAPdVteVgFAPhlHUdtaRNXJTd7z67qNNgOqmxf1Hg/wdwDl0iwwQ5CT5WvNKF4ec9q8NNssPCDo9rvVxrXVh2ySIjkfFJ8GpBQa8g6mPGuqAiaQed4OQpgMpwoafY5xodJYtc+Bu4gWrYhEa+SAuKOkdJiSE7uTN+IoLNNFs+5vAhvY0XmCjNSixZP3Gp2JzN3SXVEpwkmOfyKuSdbf0x0gsg6v1Cyft3V/ejpPFBC/FpkfjXhKbeiu2ftiZ4F4x3a/Hsb6e4Hf2gx08odOHNyy1CkZYv+RqIsKIvCABjtxG6AdA2FTV+N4n5cFFeZpljSHMoKBK4KFdGo9VHLRTGSQYGtgiH5tbUOzf+JxEnMx3d2buN/lu0b3Jh8JnhXYgBqpZ3N3fGCougha/gSZYYfPa37TSKVzwWK77CXD/8rTAz1sVOPbK0H5bk/m52aO7e58ReecXp8XWYynQHlSx2Zy+dRbAujdTc5+TjPST96ZX7ocZcqDfhpdse+/SIGWDtYC0Wtg/fBD3c2NIobViE2KcaYwV72XKAc8YGJ78vdN0yHo6sJ2wDZTrvs9M/BsiAB1XBs4lPxvUCRfpr/tBeVw0LkOuJUZWEzIuNr7Zc9Ec4dtee8dXsTdoCKlW+3uq/hbn0JteWnSlmZfgSDpgi+Qi2XkImhUeJRNlpjgBBWY/lVq9oPoTU90t47oRXS710qy4086l7sv6Ifj0BaB/dFVxkJJFo/eRuahcck3U9QVCBJjp3rogDY1IyvZg/7NLAQqv3nyZY3hF4GMBLvM5jbfcKXKb6qFtr15MbZ78YbA5gYcW/KU41ZH+uoIpMhi1vNZ4h4Xmx+D7+QLTsNGkg6egeuq4vmAGyjs9LzS9ChiUaYv5TJ4oP0yxCtVql+raarYC6jxfejRC6rX8MEp2gdbsqvqo1MfcltTdo/5ObgU8m3Rip8QGxqQ5s8eIRRq7xhYVwczBlZazNUshFUGFh5UWh771ygggidbHC9mZs/Hi6/z5mDFPRaCJeJHsXXDwT35odk2DrBzj88VIJKgeyOqqollXg2bPUlSEHVKBJqL+Gr8DqZcv6anW7w5uk4a8/G4mNwH2nijmcx4f4iN2Md5V/7dnkLSiycV5o0Z/ODQD1ymJSaVirtQ9JWy1mInm1pk4WxKj3hVzvakIPPvcV5ibG2PVuaK3pzfqTznecwgWOxHm0LRnSR7DhJ58y3AeqQbjdP3Q14j0t20D4i1b6/b1k/3RFTHJ1hmDFuH/epR2X0f5jleHjhdan6BDdQ5SEgWG5n+4XZ4QjCmSfaasDxb1+vUg30BoxddP1MKICht9A6srdHpEmrLeiyTYpNQ/ctCcj3Nrv+argQPyLT1XqavO+OLueYzOeF3aGG3/omLe3UpVdogTY0HBFayH7PBz7CAnhc3lOlCVWQVRVWVmx2gcssFryGiIDt7fWNFeXGrE2M8INLM6Cr4c7N9y0FudSFRuh0yT53pcwh2W8hD2YaIX7spcv4iUpH8z0qpoqv5bfvTYJGd0lMgqiGpoSHpsG8TuzkkJJoXJmVYSS0RsLfP4i8NstFpBDbhNOqFj1gMJt94o9vdoBVehQ/RTtcOng6AXg9Z9BQwibIjEXDaf26u8oLYEXVl8l5+oBT9LkPwQmUBI5v7PoToYh1bnzPOs+o1WuOQLxNMxfBlrj3fefE/yVumSlbIS1lUTQIrXzj8VDDSW3ZZ3i+qC/esOQZ6Ju7n84Am9Pi876+eAR6w1FvB5wMF5wu0qeZ/zCbr8bctdK2Vkhi/vcHBM7Ia+BE4JTBxXJ832abBwl5hQsy+hCbM0XxEjtxXkR9wY8FKk8T7EsOTtB2QpfODnFJ+EP/b/BRb5+J9gSCbNKn9mGuaXmEAHkDNMGcjNR4cufnvXunuZJVhM7Voo6P7ZMDLuqT1VqJn2LPINJCJwnTdeK0sg2YvSg4qTxQtWyUh6I2a5yTEPgYnCkRlVmMQjpM3/CVx6QmVWJ+opxH0KMmnlx9QdXKPviqTImhjOY2MDLZUmRrpFTsunzdYP5f7ja4ypB8kQEZcLMgkX6O+vbE6XkI9PqBdGA8wbhJ3ol2gmuVuYIRxL3iE3uABP8pWuaI9Ak4wyu2erO65GDKGT4mLrndGJdSh15arGzdRfyQR2+oG84MOXEN3QmjHXRv8QZBm0Tj5qZUT7TdeC2uKXbng6q5ryFqdEdOmTHTfH8t65M3kThsSD+gJcB/td0c+y6gL0GlEbUtx65o/ePXtNh4gsaAos6Sye1Yu32JhHf31+DkBR18Ji+OoAXzjGy37LI8aiSH6Q4MN6WquGu3+CjjF2Ex1ujsRdHvGncVwjq45ii8o4Xl7H3Wa+YB9hGcRsE89+/5yyu1CGY0RFD/JND0/KIHt3eENirhxySbzlUzQk8Lwb5HNvAZ2laOIRYydqfuuS66bDR5gf7BqaixPt+iWz7OSuoywZrbCaTm8Ovfza5LKIW4hxnA1JmmyU2LBXQxFTQulZxBVNB7wz5ep0LQ2u8HTsaw/CHZ8Yh1sNimKB4RLZeMBAaQCs//0tI+G0PQW+GbciJhL8ovtV9i1WwsegCDHDSkIUqXl529ij9oxWt7UtePoramlKxJwZ6pDHeVuvgkU7el0lO8mpelLPKeB8zsnRx+Brkqk5h7jAUlGH3EYchxXi28/gaSzCIqCu91+pb7XfjuN/h14jjhnuf/ZtDTGaL8ybHIJD6iUx2Y7LYqPnteDVo3FhjxaHZzCsFWxaRc/o0ETxuRoC1YaDzJpwuIy+y/QKniAHfBib9y/7Y+7b9B5vc8xsn6BLOf0OBwP6ITuP8yOcgzDVjsd5ezCV3hVd2+sqv3bBnE+A6D9BUKD6KUZgkG3wgPayXGUqwjtpkOeSX8PSfaLidnji1ICN/tDBPZ4VUFduAd7smpVvRIX/9uUYgk+TejXBV5KwgNIjvGA/d0eKrTDb6A2HkBjM+V4f+PEHA8gsm3+bRhxAar/N0cHoeMb8LGAfz0SFwA6oYBhlL2mp9jxAFh/+2F9LtqR0IHPBXZFq94iTswsGb04A7v2Bl4S2O8q9aOvJTHGD4omTE7otXnxB5E/vnQ5pl5R87WlfL3PycpWcrijDw/I873VXr3/VRVFGJbkoz8hTyRhOEydN/VU5dzh0iJ8YjENW+M7e3CKu7GVXPzXo/LKdSpgwRq8Xha2fVsDXMsD2sxrvyKbWIPNTi1UOLVlZ6a6c29sDrezT71Rb/ENAB0R92PBSudjRTPB0Dcm6KPxHByyBXnVObHau7PdVL58OXu2JOaKTHAnZNQShqPF9yGBdk2ONqvoZXpkAkbwgMvlEtC+L9FXtqTjMOBwy8+htNbWQX8zQupgj7ctXAndDP51I4/JrOSFmwUuX/JvNce4Xte5+sAg6q8ZZeV5SRIizZwSmXxrPBFZFazffz+d9Hzp+3sap/UiM/hWcCF6R+dG7U8TY68Qyy5OkMlvtAq5gDhFnBe5qn/yct5p/2tDAX9Mxy+VUkgksdmxG4rYxnJJnZUQp2Sind/FiFAznDNx9zN1kTjFIG/PtY/tqvVWyzPJkjglDFMSG06U5zlW137tqbr4GTQalnVxdr67rZnQ+XtM4MvsdMCFJbAFdvBNkjgHV65dJrAGlzLfkL9xsvhtYkFf0lNe5jHq7Vy8tg71kMqbjMxPT+I5ATwJOGUI1IbwpKgUSldROFdZ3H9jUNhqr29zP8j4+AdSLq59fHykhzL1yf3BzAof2FGBRDPUZ5FfrqM59d6+eYQsSZlzpbRxgr5iwcvT9Amz7rOCPbbahvBHPU0bqbqpz5/3rUp1ldvqWyPFNmw+3f41l4j1KivRDhH0FqfRyBWrGJHRproQCJFUIc+uyBAglWJdEIYJiTcnmPR7ldBEZS/7S7YhWdTkVjc47RhWr34hduygu8eOoz+tnC78YlvWYiD7dOBdtkhytMpdMSF5uSfesXEjLPYzmBA9JyrryY4ARCEAtxMOHWTLSkLUtPfFvIMQCBF+peE1ULkcttj9K16nB9QQs58XWd8XUTgSoeEXt633Avc2Vu9S1oGi+9GDB+7EuNtxn6VXHwYutf0KmmpP3Cs876socR+DbIym13GysmVXta6lmnCgJzUXX8E57taVXkeA1ouBnDdktdapuMH+3pyXieI/LkpVDB7DS/aIr9XEjqJmIRSG8JHRhO8SDfaeCNtstirrtLBkr4Ng0eK0bhr/2v6LH6na0ENpZs4o1avH0qa6qZlwB7fD9Q6XKjim5nQgCxP/TBdrAc+pqunq5dZj0qtrT75+3ABa9EBsa1pO8OYPW87tA4EDNZkO2HiOv2YpzZJD7OqqLqJPp3996Wdngemb8O9T/b7R+i8gJwm0rznvlzeHHbYR/u+8qOEcU+z5OcTMAS0DZjTQZysaUbp3mF3h1i56qBKqHldARmYzX7SFLCg7f+/Mk3cN3BYaHUQU003J0jp+tuvFcJan7Nf23e/qePYJAfLdWL2eqpiRutJEq/tmxntIN3HkRA+TG6LuFCEoV5sKflykxqvLBQ/IJ8AeSR3spd5IHYzLheV7J/2steJaZ0auypemfsgNRUTu0uQJtzGmxMiQdj12nUpNwX2W8R1z4mH7dlYbE50yW+bcT3CoYDH13/7LMc0bBQfe521MT70LPNnr6K9zG4vfvPNJVXirzJ56j/txkfyWGJZrOK3AcKe6wSim6wmD25h/X830aqL5DDH7OIkRu2KSXqtXV7IDDyLN3RXORIkr8yU3tstqataSs99zwPyU84IHAhvEm4ErHjuqZz2CZns5FZcstc/1RXphtNRQUnf+P8OSkswmF9KvUluOieW+cAy/ZpbterJlUIm546znggwepyl9lR80aD43GXcJZx0ql7do9rDPvi2JHvf1uqfjdCn9oYL5ehqDKKxcVlMEJbsipQpTX4U3+yTKDk9HPr41j+lNHeOTNvojflDSazkDv02BmjkTsA5W74iBHqm/YC4JSLinM0Xh9BJTsZQhZaqbLtc6rl5KFKCFkf640a7eDfXRarD4EFwuHhLW8p3cJxzmqaHMGt6/uqtkY2bSykVenDeNYiEWeHaoNbSec97w/moMXFuGwMA15Cp0pqvfZtpcC37aqQefTqvTayNBuz231/x/dqOCEQo5grQfUcu2Ws0hbXsDYJrbCYlgEv5CVI7eLRyXl+0HVj2WCFO6kLMdrvfOcaeR7fu3PntmfbWZ1+brcRZg/RLya8elrKB+zACyl7sQWUVxUghwKVMlIwZ/kKob5H4DjMYx1IkpUK1/BdIFY7nGbKx5mxLqlKVWP7bMbvnFCvOKfi7MNjG/UecO+zz4jdxnJHbZqvok4/m7QhFJnSmCh9S1Vs7o/w5bEJ4HoQpdlam9YPoqtZln7Z3+r+XiWW47tJhXDmqf7Yvs0gxVZDSUqT89pdyt8hZUmV9ZfD0F2fJ7/nal7PK5y5PrcsCZVba+/kcr+1/63dHdubce/6fZYc0wfqxuyTYqM6tPKv6Ubcnn9aHKvgynHgDZPQr9ABbzZyT6CQj2LA1w+w6/TDvNH+YsyAhU+vczj/XfUwZikFeBjgbooWuU647NdE5CoA3DRpxTnVRsRqDl6BaIS4ivcFt1X87616PZtqUE2rtSEKJVD8jrQ0UZ64c/3p+DMtiHdpYyeNhRgeRp6CECN6jTLy05DSfdgwBUfJsD3FyxG5htG7nVfHFALzHQu10sdGWWtkGfNjnRK/m/snQ84KZ5fCOu7vnDWm+hqnw84Iut60yoZdSbR/YLevf7BD96jEzjtiuaEc53x8vzbx/OAcDETscVEtCE1niCD39SYo58FFC7Pte8YbS4QL6p7NRiI0MUO1+0FrQ0d1zy3q76ZBh4KaS9wp7yFVWTQlUZ8BVgUqg/VgdX1PXLW8vUzcxDj9P4p0CEYt9JbN/n9ZdsJ5mprRImdrz/fvyyPNbJXCzOhGQaQiEb87lemM6cmq3p0V6kuTGlF52W16vy/XB+xOlNVX8p0RtfnU9MK1FWxbRfUiVKkmWUIJCIE4Yfwc6gwNzhcNaTtLtTSV1Ej8G1vv63ihN0pWdq5FDpCagnjEii8vf/nRT73Y3w3waua5UV+0lb3Q44eMB6uzkja9Lo8gfvoVenTG7B6GVAyraeVsVktGC+jPhQRlELyq0I029ptLQE8m5fMG4fqBIkp22cb/JvCHfFVYNT2nm/NVy4uPRUq6qLgjI0Yr2uO0NB+3CiBiNK9iFJvdkq3tfrBWWRdgseO8fhqScyoD24alf+l5bdCNL5G7h+SKEHVd/tGVviGM2nKiOiLJPhHOVk3goanj5xKQHxY3yl2qyT9T8UOiW6sKuo6oL2xnTMSb3kC0jO6vvW4RLFKzP0SZbUvpaJfi2dd8rNoym+5qnzXPYCawFN5vGtOeN6YAcjhhO0zByM82pfA/U2dkracMYX/d4Gdv/4S86lXLu03+yx/j14hzuTopZ85t32M426aGcOYmwZpLqGO1CrxjBBlNUrSguC5dQNe+8mtsxZWJpY4TOn5c5oSRtWbif9pq95tJo8/96bgtXGr7H35PL4IGZDvfcJK/chn0xl67SS5CBeN+9nirYQGWKCP/W8tsmSOwMRfbj0hDIpktwPsCRnQ3njniy2bipR1RuHtjkcaSZPMEn4g2luxGUdJq1l8x8dhPaN5UA4KWRfDky9WGnwNKiXddLfZxHRMNSBbBBNKlXIVlKMpCyLNXl7RjXSap7RcwWfRnUJ5pYNsDTEWd++Y0WZwn6Szwyp7Jbelc9UnYxPtZYAlstzcMg58h5k19T+GHR1Zup5Sr5i5nVD8nF3W6cFxAFPdVBkEeOWdfRdOxq6prGQmavJahG6Ua621nZhSbxANq24/50fwiifIVXzLRRf9yMdG4sWl81lPvMjrtrzNRIdECI3n/tcmhtZ4Hehi7/PipSmDQHErTLy7JnKbLMfKOq9h20eEDYr1Xmuk8+r1ym5UmfYWrNA6isa+kTB+b0n/vI5NrGLzMxHOY12c9t8LKxRz6pHzeU0XAQrBBuYWT6FypxLcosZWR4YU34jl6aUZ7Z6ybGrY1r3cI4tZYxG7dPdgwJRb0OsMtE03BBWboOwy8yFpA1CXqcHv/eQGzR4Cg7Ne86QUymwRT5QkOxIfk3xqOzVXQmbAd/xTFf06Gbm2siLlw6g+rv80/s4mgbeAEewmnr4+DnFrbR1ReB8rPQNTQpfZfYBC0MEvy1ueo2eeDLb18+FX/o5a17/y8kV83qL15kp+/oxA7EcXDN9FR5yH4+kpR9NPSdTckg4KMzOs+BSzJ4gea25V5nbDF1fRixqjGv9drEWXSvbQ3TuPNBeHZnwnXMWsBAT1pQ6Z6Tenvy2nIsH2NgUKPgklG2+NcDMLKbzl5J2wlFF99BSubBrK+HT8ju3KphljAa0qht7VenxALGHvvNfwDtx8EED3EN7r3pG7K6e7AkI1djPm6uXwvTzi23HO6t5sNjiUdr3Y/8f262sqpiveEAIkT9SjaqH1yZ4NkPdTFwCNfZWMRWg/1Y+9e27WwLxVpC37x5IU+fWASho3g6xAuiLcmIDnwdPQhQA4upqMdKAe7EQpREilFqq0ghAmc1GPi/rtoCa/LuHqV9toQK1v51FC2j0P1jfhhwTXJtKLfDs8N+Do6v3h32+QPZaPMBj5eDdOdDVdYWE/1/fz5HmIw/+Wo1YlttM4vwvhy5fohcJ7ScJLrDgoE/45eCZyWV7aBPp81HmCO5Ne7smHRw4Q32kMKfdVbt3qIL1YVRGabbud2tm1SaQflEYWqyDOnQuDZr+kg4qjSnNF6rSn+si7eRviuaep8QDErmxHYe7+oNPSBSN9CL4USULtTIKnSoPiG22/G0HdBsjN1LV7tbaNaY/SvfBA6pBGYr0nUsLQqPVswyqIrSunQSv6bPaIr8iev7AGPVASC+0MwcPoAJ2Ly0bnr92LT74qLKpxD++zevdfMFri2OEQ/0rovKZZuoVoxTbN3XfGqs6P53L1nWYinn69e1CWqPURk3misDq4RPMTksSH9P+/raCwEp4gp7iYF/L1PNj/7EWnBWGqyypeW4N4JuprMk+GZ1O7lP+o/FVbM35oG9qRJ2wuPR716+Jx9R0R+I+IwKVvwyNWFss5WlvX09JeoN5xhxEdRGfgJO5TY2xO0ZDV7dmf+yfBDj1acjtFCrL+ve9e+VF+WbuNRrBMOHAuI8qQzhlwlIo9qzVDDTpw2/Gv82Dne2UeRqYRW80MN9vH5jvWP+i/gYAfw/QpLVYGKjEnuqnPatfGojmsspoT5D63Bg7GfNk7ETwoR4/NcHHt5Xa5GrjHtuUE6EL2/VfvRC9jFxdjoc4OEq2D84kFvWbkfm10aILEgJzNWYXWsuCqbnnNZVCHjzit6kNKj1wGxmueekuQRMv6DopLPOgvuqaXH9JnSTCf3GcLi6Mm5WvgSRCCLV4Zplrrvw4Kq1Tg+rQPDr90V8dlBR9w9MZNjKvyjQ/UEE/W5hzmcEwjSJtYNxcNBmzaRfOGxjiCw06f+JsnX5RMDwNcqfHUkBcOPLUFE6c6ezthiXUnDfnhpiH64/YF1NVm9rHYaZGKvCiO+oP//OsBB2T6F9FoRTJa69dGMxIul6SX7gOqT+TmLy56D2xie0UVXLm107VFl9H+ueG0H0FiRXhsNeFhltiFeESp4Yf2OqAJ4ssrMTohaljzE7zfF4Dxw9i9CtbvR41399yFH+Or1DewQIM4Ay5pieGA/0P35xvEReXW3w3mP1IggcQrWLs2Bkc9qsZQpURW6K4hBruALcRVTvK2RxmdkpOgQEjuQ+3IIaWsUkCj17Lp6u9z/pPNStX4ssRpyj9TkW2C89+Sk0/BZGOx+vzn2MSiwrAGJ9JW04PEtE8lqpX3myV+r8/PGdmGRPPpeV+OtdRCyCW3ME4l/Dqx7JwNUOVNN8q+ZDFDwB5EFTGXDUKqhqpkUtRXTu22IpEfcGGlpjy8mkLKcN+DgJ7gTV67sDNgkESwOPSY+vZiNFwqYHjXh/5t6/+wwOWZMrB1h/NT3Q7fwlfIpBvwb+hqp21Z0skV0ndIg2hPYnsm/svrIDQP+B8xdgPhkjzl9bd4LJxtzM8oL4HDzh78n50lbq32Cwgfxy8Jbj1vP3BQdq9U5M52DJcaeLwSjMxN6ZyKXhHQ5Bh4sWeLYM5NihgsGmBqcm4fesknBx7OnVWdgmRM8zN5Y4qWrUBBlWqN10pB7RLJtY5fV1Meu2AxNx3K5OUlT1+Hp2pXVkgcZGb++b6eHWm7QRHMSFXbchOP9pdFqJqnHGjeYzE7owkqdQ1K198kkFAuWQHYBZxUzONZY1MscTWazLaxiS/OihzPJ/GWoRKu/dJTNiYD7+n5+zn1IiaeE0kjdMcaExJ4WHVMxNhLsy+EETpz+cPNQ1k4AEK3TG3BuAUNjXY2NN+p0bGVUmoufpogtwpc8697Ojl1hLDE2JB2pMWdVF9zqVioUwz7FaaoC0Rr0TiQuT8Rm7cRuTIaaNtW/KMVmSURCHdmEW5mZTnK7Y+xgQ8IMHB2vW+hHTesAqFYQl8tM0Em1qVn/xWCcq06fzZ0714xdPAK8+YxagiD+zl+pF1z9eKOXhcfSM7dJ3vJWSHOXnjPROs8rpHPjWO8TdqIyXV8GaEca5o6K2AZSCdMnXBRqD1rZmctNQ31rfGU/KGqLPu5uXlCgDyRmE+SqjPRGtqqQocgCE26zwKQG28+meAdV5O4AuB+GcEBZGx4fR1JQiJjYA6jZkIlF7InUOnaY4DsxDpwnep32RCo7hh51IkIVMMXMllP2drDDewtwKG3F+kzbHzwszlr67/CLC3qxhxaBvziM5kxAP0OEELxs5X6TrCpmTT47CWpddsTaUfEpvokHgAj+Pak+Kz9/2FbvAHxupVPnMaMuNrE47fxD4mhbJtIa5enF5D0XVW2hMVUorSrqwTkwwa03FIqYlheQ7d6q6oZn9pTbt+Vu9889OGDvszhoSI7CFeSzualqp1mYKqkrr8rLFl2OsE7O69/gTo2C86s0ZRS5sHZ+eFSPaUKBHJknYV2+y79BGbakOhY7tyLpwzUvGo96UvnTQUlOnFNVRd5czEQ+4m/yXZOKyYPVkF4Pb8R/VpWofHn+8EWKKXFIZDJcjLtaJSP1dvmFLQOmcqG0U9+02USOvyR2R1shLxNGczq0Sm27mjdi0SMVkwUNy/NkbzfkxinJRPRN/sFXVV3OcU7E4DKfPy7b6lvXKRbs1o1HtaHyJDnAIpdyCBLJKGGK6KfmWdvuoGVz3Glb/XPe2aJ7/MMcFx/QwZ5Uu7Ur8ujNAUWQs4Jse6qcOQEG15ZqM/3/kuO/owWxsfa7Z058snQ98N7m7ZFrGY56tAe7TGWCqdHVpM2y4tKRNYHJ4lOLbVjRztRiWo7MwYfQXf3lYflRHdNaCx6I8FcdYkbOs9ytctdT9Un1MwTTGp9y5mc96QlbEV3nFWvfPmm/gYy7Yy3Y9dv7evaEy+uzdfV5jq8XXqvX9gX0O3VmWimnY9lYWRavrCAX3JPk1z7Kt4ZX9gHrr/xc436LTY+EX9OWi41alj1D92+9kddlqg6CNJW7hYzl6sZNsCXKYAEtUDf9eyAYn7ONBiUtT/yIX/t6TkTnvXvvGM4Fr1KUqmJdLALmNORRTgswnFA7Tsr+CyaOWWn/CiSk5yoZAAJVvQz5dQ47oyj6qMPaQ/fMrB6ad31crCJYcGUFxWfTHlrJLlqvWvnRHZJPDJ1mieULVclZFBLz/E4KAv90pWGqSm58HA3ha4H3UjrcSv6cJCJfHX8V6pHY6pMa2jqTXmtYAOR6Zpx/yfam5O9DRVx/5idvFL5+9NdBKuYbuTZdxfxSe1Gllb2+pyImezczNKXx+5FrmhY57BioHL+hWu19paVUNruIHcc8Gcod836ky+P1RsCr7ZvI2BPCBX+CA3RF2wyRYEzcs9zbvzZVMAUFh0XiL8fGnWtVr8TRfQ6PsXeKGgw9psCFKaeiO3Xkk3zM2+7Ysffx8Sjqog2UOlTm64byRRfrdF016ms13egVZw1h//tSKKPeph3T75aE/35UT+vPhtldjIpVh0bH/CnBbVJsQtQtFZ2/6lNtuKWhNHM9i/mXxXjraaraZe8YtiWrx2fOTop4UX/zjrevzCIxX6w126vlo2dUXjVM7r9zloQT/EvGG8MnZ2QSlu6KUh+Yr53Lbx7jLo4eyVp5Iu060KunuZjnsBbQnp+Q5hKmmJZUNHhGgKf/iUaT15gm6pJk9QRTPfTFn/ckQjBAXUXCO0vwut0iabVddditXqM8XqV9Ex9oD28r1n7RTvPOJhAxKLYnYS3njHJE7iJqihJDpXqp+9iY/KnaIj3mh556jhyr545v0VZEb6KR7hkFqnvLWoV4dVfbdfD+KOKnnHX7GGWlVNMFqzQ3Oj5dV2yI/5TipzjO66LnIeDcF/2HvADw6ZabMTZP+AbhbHV+aVStTVJxz9Dp2dWMsKRF/EIOnvn9+LFep9jYI77bFEyZdVPGb9Qwqnh/uAm+xgzOb+874ME02e451v2tZiC9ZFSuJ6WVREHCe+0lUaJxhdCbwZKuWG1s7K8rnwL+knn5UNMV4MSlBfG1z+xETaAvVl6eVmPz19RJNvCxhn+zg6JVKKOis78WtVYMedxEh/u3PaQcdH3/fuQz2V+ZWyiVqEa2pkoDvXwv2NNEc914fBjSLE6M5oSbWFK2YtE47tZ1LULhdrl/R6YLLc44quQnrJ0j7GpMEEevpc9/8G/p7keWK4xwR4TN3/p7avDIoj6rYdAgRJAsEJBCYEggYSLDgDBE9wGNwdwuAuE5IAwV2DBXcIrsGCBHd3G9yHQUYeeVWv3o9b96tXt+r92F1dXV379Dln91prd9c5215L90GfWytPdAvL3YeDLMXXZsMMMwmxHyYjNJRt8fXYWneibLBsmNNcw/BeBhKNlj9D5ImxAsuxqfg883qY76kmIUH1AWwl4mwmLgzAeyIpfpnRPPGPS/QgNiOsT5vyhhn4VB+kKfIeKHx8kBQXHz/JHPMoTXjim+viRdGCjmqibbwTmmIQOFHM3AG1o5EJfV81aml8AlQcap399GkWlkjRvpdrjgHQPWNuUrLucXShEeHZ9HzCwTWBlxO1GilAC9HUgvOKSvIMlikXC6QVbfF9zRU4I7k+uwaLr4rvCDYdoKEfJ2sQWrL6VeR35A83pJQ9onJ/smAAZWyMljk77zjHfgGI9AHEdvNTeToFURO8TZyqMvCACqg4CEur1il2qW3qK5s9yQ+8FiLyAAsta2vsHaYW0iEVF5+Juvl0N23Gpph6T2AiVK+UI2ALawp+VcxFTal1sjSta8w458RKQlZv/BvvQeDoRGo6fQKpGCuWPF1xYTmriQoj9sIXKrwTVe4mftrmkmQIgPzqQNNd6Bs44vODCb9sWGEbz1rFoTkvbXhwYvv3U/atp0mOdpU43qJEiaWP9cl94Pzyh0yRFFRzPpOvEtRbPEfsis30PyuwAAhNiG6Y0u+wpsY0uT5mIToEsfeh2cUmwbYFH3zdvK1j60uyt7Ik9+CViqeIz0duq1ybYJ3jSuEy4PkI2b+CvgP5Mk/6qJtEGEMmkPzlB6XoEBvwItrn712R3PWsmv1pF1M4CqRt9e8HctmYSQBz2xO1LQDZeeWyZIdxdnHcYmbiX/YLXxs32QjwbboU8t3pznLZQniWsZDcZQkC+NhN2/jSfnGXFlVVAUr0Ya326H16MRkWelSFxS6BLPHe9+SI+7Hr/fDn6YV2jfqVhpzf12vtbejdViZUeAfkb83b9yJuwXJ96kt7Wtot1k+YWJCFfQDw1+wL7uWe0GSU5h5iDANQO9ImPLElYX/klcm6Ra/4DbJFnICmK/58EQUX+wM0S/OyXP8ZU8DdWaQrrgXbta9+82toUXnIz/Hr4oM8JvlWRMl6KJ3t2trMd0LP+5SY62wKDIVwOI8JlnlrDMQG7i3kJ0TeCS7pMsU9JY8o5e7IN6Ol1fdsLhW4LKERzZbfzMU6b8i3a63mOf+DUmJyGWbqd2edrm3Msk6aOeq9uODJbFee3sUAiOHc7nl6/SOekixxfXBg4Xnl27aYutqwIeWzKCV3EPHxykCvGvfikz/rgZAs9tismWI7Byqv0ix1W9KbpCIXYrqiMhV8Y4JDjfiJMDAffx0tRSYzrauR4UbW49BvIYMcq54UhxU/g8ztfOwMejWLYDPf/kyPpp5ctpSyCXAZT/yqXGtvDTLD98C+YPaZbTowesbb74F1o2UPxE2lplJ33ufVMzpQF9JdV7Ol6vgy9iEaoaRrz5GivRMs4f+O5lZ4tfNpTMvYUxGH0ngvHjwDHLVrsIfEuuv2dcZ6i9NZM5WqhCWjIHNFaI3RdrEfX31jguIZRzVqKSpxyAjJa3IdJZaHwAYEkKe91KzwLkwh9jFccq8Yga0PDymdK/V96tON8wKqakS/RZNgAPA9lxqQxQjUK2+Fw9uPqoj4BHhnrYEBdBGU8BQTtDCKOsukoOKFMlYug2XonPVn6R9NvwTupwDzTVa9fNWD9F9EZ+d0a+oqe0cOhns1cSK+w+wQzBWvN5YNam7aucRdI7AWbW7BJnH6rNK8Cyd9Z2ydICN2wZM/Pbk6pMwm3id6zHH8qjbywYZZYrYTApKKpXXOam0KhVIvCfZGvMp1Q+ZNowDekd4I11nknZYIzqr/U9EgkdH1YZ2MQSGWrE1+HiuX6Twf4q42HNGaAzIuqYCNx1EYQO/0gfOLPrE7bbG1YZE7ga60TwBT5E8O2N3wBRBmKOrH2lFGX3YYVqvOEiRxcq1RUSdib0ImsnWXw4+TfgsQntY/WDe3mXjDwz1PjT4rqi02n/SU32duh8LjhO5+D2pTx7OM1TLMHN9oRo2LeGeJoCWO8mnEq8qeOeaao2a/fgVvzlxVWOgBNayc9qLt5jXtlTVYHqLH1Y4hZcko8bkS4ht7Ep4XGIC3ylB7sJ1lhoXEWXUV44tSyGMxyXyHTwXi4yHqQnQYAOGmu/2eG53C8Sddi9qYk7dBm5mbYxFuJ5oTdgeyr9hYbO2iygfSY4elZe2ouSb2F2hTLraHfiYA10ftUpWdQIQ7sWOpMBBprbR0uG6ohEkX2xlS0Rf9sDVLI/rTzvsRDKANDffp+2NMZptlTqm22ilk8h6fzgJ/uVoOe2+mtdnqDpJ+8dLh/KybfqOEat9Vy6C6mWdq8pVR7XrnRmwLzdSDXkm6w9cKd4vEYzMHvmE71Vqhz/q3zBeaTbpktJ8Hq3blp4D1loKVEzM8PBTuEdC9VOYW7H++A7x+mj0ikubdQf8lGKeos5soZCKO8TcOBmArWUiKy2A0ZDeYtIABcBCt1PkMajRW+Y8LLqYnQDQxgJCZomKNzr0T2T68bYYQkyXgSJrHw3iRFiBNKKNWpkQI+gfXNgbwuw+UAZEsZxqg/UtUeP3Tf3r7oUkI7HHIdAh8T50j9kL2D9mykrawb45/RrSBoeJg7sd+/2fsWo31MesQU9Dpa6jweZG7gyxFl9EScSnsZqp9sTkJ71ZZ7k7t3851OVtiuqaveRpN98tob9RvSKHOfetGYFFJv8KsGm7EZ6s8eqbfdOpLGECHDvRw6ojEhT7TLP4u8kbdW1k4l7irdcgr6QTt1YkBREPPNNc3fO/PXpsDTwX+rbfUE+uOucyIRE3eqH9i/FUpRM/RTkcCOtnKQmoBT5P28QrGMQCHfyszi6qPnxfmOlzxUZjPzaZDu3SL7gkGfvG/F20Sh7s/FeLAAPzbMQAKmRiXzNjtdoTKtrxax7b87WwaKAyOt28OUof9q+Su8v1Eh94EA2g33rCdf5RweY5/EAjnm9gV/kuNAQSGnW9W7D+Z0MIAPne1ryuhZ6apnZ0F1j5DGeTYgWz79J/ERK/bT35JphHfXEegiKCJ3vZ2NKVOEIgckpji0ag3y+1iKHRNI+uscCBowKfGUJ9lJYX4+hE0SNvf/GP0iSHxGJTXSEez4dUYyphvIjwaHhvdjQGUyySbbItxqZDtyYNmc6GLMujUkuFNTm5hCpDSMAZQPZtJ+c09PQAbA6iUp2fe8q6GNrPtzfkVugpEOSR/zzaDHiRjAOT276C0Br/9GnWg7VzjN5yuksCSBYXoW9u+ix5BGZe+Y+mvU+kYwAubll1xDVljUjsN1ConL2ouHIj05Ve2X5ZaM7NPTfGhWgCxRx9ekAzFARFkwCEMQNG2znjTD9rODJUM0za1kPZgGBwIv01zXAG9bLgbAcXQ2fX2m/clYTmemGWSVOkjrBet9fTIW3Jyg6LebUUu8ZLdZ+r6exp7sRhAboiYpQPsbO9Wk+r9iGWQhGzAW5DedEMEa6ScBPcH0+HdZFcwaHlPafGIN+h+BlhAtyTGAyW81qJrhA1FdHH6i5XyDPdTEygwtDoKDLJaEqeis+XaEv9D3JSaFTuqVwHLF/2q1s4pEXyVTWig6qNB943v20R8bM/b9DQ8E+Zf7rYChnL0Xmqjm/pPDJCjsJX+zYJjVtkpcANL7Xd6X62NRSq6fQ4nKdUtOL/NLs3RjToLtlO/1Zp5EX1W5Nsnw7UwOpUx94rCzmY/AeGq320LnOWGeCPi4MQoEjsWDo7g4/5DP9r1/PHXSefreFfpm42jMRkJvhhApPvY+5Z8JvkPFhGZsJW61+tg59Y1HyI47N02R001R6LuI0crokdsi9rIxkSnmAgEk1Xs9uJL6RY9OZw8389r7qPZsHKdkA9paw/W5NtX4o8DCFb3VxPdJrK3KiyFS3ApM5f17VWeigfLjG5r7bDCWNdRTq76fYrB5AuQZ/gYQKZONBDRX2aoOPrsvGLLik50SBA5ynhRkRysrqdAXTIsZjaEkNTKNyoohdqJUj14NL1AvW5Bxz4pfCz69bJCOCGdLnWcMExxd8MdiNNTapfsmexa/wp7QL5XtL5P42ChdX9/QP/RfNmxZkjkQPsl//EW8WC+NwbwR4lTq7xO2rjtLtUJRAEaCtDcnYrzKwubmgy3dx21wFWGCmP18ZvO+lxc8uvQc/x6fub5/jZMnm/3BELIW91oUFJ0txqJ9UtdYqQhJvHZa49NwRG7mOX+zP69tATTD9QW1Dhw+j4KM9m16cVGrkrOVQTXDtmO+8iS1jNJDxE5nLPL/FdWpmKfhlUIbJKaj2sY9y17E00JWto40qvZALKF0ymBixGZ05XuTD4FOVZhE3Tif0hxnLmmgkS4RMiQByzdngL1HrPjDDH6hh+eNkkL8rw8ZoCe5LD39De5W6A2ZIcKTcwCTh5UiOhM6zL5YADdbTqi+KlrTgR8YGB3y6OU6WfBD10nwn7wVPqreBctCxDGxUxRWovFibiVPl1gMg/UCBwW/0xDTsTmxGaTjcNObBdavgkpYbdjfRCR9ol4GlfLn3S5/TO4hxwrqpmiEY2lUREPyaXFtVGT0BmKl2tw75SAEsLgxniLBrKLqgFaCxq6ktTZxFmtKmtfSX/JABHD3g7H6VfJIoSFsLDbVf2JzaYGx+R07cDrSek7sW6eXvHGfBPR0whidJsUMuwX+5GBm3iiYdNVCYm1EnCPlH6Dee9aM67CM1oL+7KodhIdtw8NewecKavOGJJ1bXgxxctyBpSby/7wwZ0OR77x8kZGvxdPbU+TzzfQN29+2Vrc7z7w0sJa+xwnw/6ccPO3JEVr1oQ6iTa29tyrgJrRXfY0BTYDAtdDwSKkci+d+sSndYuvEOgCGLTBzlpoAHPCcTV8OgfL3MmjUnewtGIiWrbJRNt70c1tsHq0fvbfjoDBsK8/94nPH4SNCLDqaWlyMjkkN4B8pOlT9mIkNWLje8D6CRnoSQcR/K1wyHrcqi9DA7Tm4jHFyUFaSyjXTvnIT8YC0f65Ch7yr5+9n9+awM7KIpXX8+vm2ZYyc+uEjES8JqgZpENlKfkNcDEAshNNxwq5eWvO6BbN73aLtAGP22xr7cM9mepaW63HA9Glt7MqtPG1lWpj8L42JzTeUn1aRPp6Jj8ywAyaUjHwgJpwJ/NwN7pLtfa0ItSG9jDNskwypQk1xsJ0m1XuDfz+Kbd+Bi5iE4OPCOmKonLZCrxOQzhx/BGVXXH8Xqd9tFPy9QYa9NGTp7JakEJI5uB67GZvIeMg+kTgokCoB6I4/9Sch2i6Jn90Z+4by873Q8bfHM9R69eaTsttGYM8LsSPeWfy4wUvGHP9ADwSt1NSXTBV1HTZE1541+NMDtcuRNrHmYslQ46bMqdUiXXAPvFP8boWzt7vFc8gBs0ZndlByXgHPerb+yMyw1QlyCg9Dt/vDnEEfPNg+eBepncuIEWNR9DRH+jX0K7mG1G12ifNO7+ypCag4ILKcEvQBc209j4MaTcR4hSv/bs95CY9K4EbnecvkKbCCYVFiVdr32d/BCICyL6Tdrq+W3UgycODyiXzZf1/q8e3o52NxLLgF4KHOfQ/QEclUzKcHyxKthAruTckhh0z47/u+f55OPzJPdpotNcnqtCzQDvuZQVtUa1IUla84EvOEY+hv7t+PY47Smz4gJ55KwzAmRhOsYwBfCqAbtnEYwD0GMCm2xMbho4zzVzxoBD0ZN6USOLwMqhjDW0iOyt7z0LAMz5grfu5An1H9J7hrf25Oeg06WPToW779TIITfoMgAHENrVTgpCQgvFjqmjra3ov0YuZ5XZSaFcyDwwlDwSD1o2+3neR5GRjCKUMvUpkPXuKAfz8CT25Z+Mjdvv4Rltk5e1Nph+Nys1a7uyO42k+XuGxOVAbelopRc/UhxwmhK4BUSXJaNLgPmQkIxqFAVyVBMCgB8dPQMm3d6OiQ9/W3uOhxW07WcQYv0MXCZ74UCGZjjCA99poIQxgoRi6zm462fM4IPZekdbuIkQwAGOnWrTxwYno3UDLYQga635Y1iWCLwR71jAAj+EgHyDyVRQePXMM6uV9twI3mqKRQ65obiD6ZVbTkrjx7Ir3dV2r0ICd3B5EhmUO8qM8s2jlDoBO3DU+TVBWBq2/bEQygpBKvGjS0sjVc/r2vqJoDKCMtVUkCNnOGIgebBHjO5KIhmIAWoK2At/O8pYDODGAeW2vFbYUt1l37EsNhfvheo8BULYXR3e2X5e8IcIAZpc4fd4MIkeobWbboNXpqPvwqC6mkppq7I3DQ2JBu1qMrxUuZv8It2+/+bfJOZKpyOc6RAuZfy8P91w10JXo97UtAcY7zgc/7UUdJq9QPKA4zazTaPsJ9zrowPt/GuveI8Hjj0JnRLnXofeNqhz9sAaPtPv4/xKHXrL7TWEApRhATJPl4jkGwJtgTGAfEms1f/VF5bRY7iv/TO/rvFGUrwKafwwDsJvnQS4MX9/jnNW/1nsRyvMYAMNffLF6lSyYSmbWZUqT9eTlvReAF9DY41lN1mm14/40u9cjQ0bmkQsMAOvfzmHgvoXar53T9yGyyAYq1TBSIuVbQQzsK4vrfAX21xG6rSJ5H6lUI0FDo/SAGfydkUOgMafcBT8L8kVaTPQbW3EqVOO9zAbpNTKPJfrNnZT3To6vaYE+/813gH6IZHpSykYKLVOj94S29ag7mbUmJSHDHNd8T2pyUIlqsUPhTNFPWT5zt3jIXyH4+v04i7uFqYIpI+WXAqZJtzz3V/VKQaFHLmARY36qwLZEuS2sHrAj+Yu7JMrSY2MkIA+V5aIfv2uzTyOGahGdBVkvrYo4NEeOinekwQoGGoYIoxZDKJyu6yURpjXAU0YMoEeT57r6WMak3Ca3ab4F+EOzjigCnHjFDpo9KzplezKU7NI6WgtB7wcBY35GWl3SpQSnqeQz2Jk66r2vaiqIV7Im5PGiLyheslOVEjQ52i3kI8+ZQ0lt6S+mAzMa1XSudl2jCnKS1o8LVxluiRWb7D9v1vG5S4kWjWnU+eNKwDijprmF1C40dfCcL0vYHriZT2b+7kaGwUdxbQft1339dx8ZWnk+Ft46u8Uyks1967wsjzxYcbv+AwaPR5iaqYLYYX/aSLnCWn/wmQFQdgujVzYLEGeaOCceKDFUsSiE3MDg9dOy8nEdbiQPNN+lxzDP7TdMLUevZ3vY2fXi91FllhoSFHIxrNcyDcBh6Kiwm9VgK5QObI78cxv/t+hV+xKRsv3YrHmGru+ykkj4VWd3oE6Dz2cZQSFHVTva8KqK8ZyboACUlYozVYqnu9G7zOk8BciW3tfwolSLZ8MyOSuOYfa23DApydXl5ELxxiIurnhc7QhwQNa7YW+JT6EMTqsjiVrDdDJUVu798ye64q/rqYyo2tSFZEijS9KnD7wFAFAaSH2Hl6+q1d6V578SvcN6CnSGxBTYIiH1drXhocCLUlPvTvSRpCAKgcTRzvM+9Zn7dnaZR9S/u1lSZXoztmSd5t9qtT79VlnFzipir3amnZOPuzUsniGyA82gt6D9La+Rkc0QGNQqPEHhn+cDa/Opj8+WdKTZ4Mfbk87ojyCB6UEDP4JDSCKHPGlqgIHRKY/e0G+0Wb6OlVsmP6kuRMhwpLmkzwRl99lQbWGTa2s9l8QlrxAhndR57qycE9OfWOXkVWzzXyuq/DPGVOyfFFtZJG7wpy0bbV6XFcQbuKE/lGKiBLOJUx2pLI7FiH2KvClyS9j0b6jwTgK0MmWpw2xiZ6q9PWOF7rLX0KLgvNi14oPohJl3vLH6zqAFM+3nEMCah6lCqoqsL1V3pKSjH8eTlqcWNeZkxJASKOOttsEm40KrRqfwydXD2kq2lyObJCroPoT+KajAftHLklok+RfdAQEHXQJsmHwI+FQXarP3MRzd/JCn56RvqD3auIiib944JMIaN4Ql7ZJtOuH4OUk//8ABPf2HQt69LkGu5lpAkK6Yx62WRkatWfqbElbRPcZc3uOOxSpgq/B6m8Q+XuWmOn/v1WBVP10TKMNEyZm/tmDhmOBljLtUISiRG45jRADxL83ZHdSA2Jfn4sTgLVOXKSlejuD+PnyjzVhVEg0VG/xuImdLjSwhcwXmRNnnjdUSVzUbrq5XaMOilvwWaWtAjYdtLVMDtkTcLlZXoffvQ6Kjw4tFZw7vCzY0qQ/bLReuG3gwsu6HPVkN5FN8eib812NL//YM1xWYTFkZ59KerTnfsVPRt51WmmN3bsMVwSWmxBSLTTEVOMUe6Kn76MtptxSFix3aLGBX4rbehTfl+PzPmxTczcni0i9CHAPnCs9vv7w0gDPyk7ex//lSMiR7LALOZXy2ws66flEhbvGad0zre/AO/7yXSrcs2oJZnFdiqJyxu8Hl9zVO7DF6r+L3bOdCPJffX+KZNvtu9NPgFYohs+b+Wi9Gg0/kX/pvFhBdPnmK8h6gUxI0xdDqnk8Z04241ZqTJBBld9vsT7mi1SlpMFK81sj8uv+H/pR6VZO2+c61Qx1Vv22erjNC9GfELTi/IqhMCfk+69aKY56zFZdU2TCeKVOhoqSva2asCDWHLKpykfu1FnMtpxOgDDpZNlDB20/ZYruXI9pjoTmLrBgAmF0tXz96DZj4divaHNa5tqwQwt6O6JEXpS2GukNPwm6x73iIjwmND+dAjaxVTYxzN9fXvGp9S8Z3G6V/11BKPi+hqxSXCpMm6LWikXis/S+f//mhPE0qR91z3W+2g7Uj3ZY3qDNjaQzAXB86yn2jMavQAOxgJZK/EvcQfzTtg7xvTpLlCzyzB3oyV5l3T1r3NA5LQRaD/s+Jjl/sod+EKF05UR509ZcGy1d+q4N7KfSpxx+IirfHAET7tuWutO6Tm49C98+3LUpSktkCPQn89zWWohjrLxBxqD32XukzFJC9VwVcI9f5d1cXrEs43c6J958bM0MvX72ImH9b4eD6f1yQaXGX1LI4PcrLMDMeCMdj8gWyvYusZAPxQlcfFIZ03x6WjqZiAH6Et9+8wH1Cbyu3NfrWF5n2CNGaeK99gW+iCQ7yvbzxxgipOldemKOrHQd+F9C8SsMABl8hizfl64Dnf6Hs2Ike4rZ1p5SVL2i3fvBD0RQrOdrMuu0nucYyFRmQNkZyDKCqE9Wp2DkQnWp17Vt0fHexOR8pR9VdLpkSYYD6kHbreie+dO+TH1k8aP7gMhLK/loE+K6w60gyfocHeE1SIrD6hJ9aM4EISmashkp77d+p1vaN9DF1jwhudJSjH1uxbnzzw5clMgUE5PlDWdbsri22sMVAYyNjL6OBI/m3leLTfXbQJ0cWZuO9IHbq0TSrmtSlksrjPsDR1tSYDZlSBDPHMnF3rRwGoB17We4P6ogpIIi+/Il/Gg59tOJ+LzU/pDWgIv2J5KNE71WX8C07EE+f/V78ABPl0cT1puiiAM0ySnGbtEWNaMH70PjNIazLLz0iFX2N68/huWZDTfcreqDprj3kLM4ZuCcT9Je+L/Am7QeUUjyM9d3tt/CLDyzrPb5O1wHZ9z5RbPodYaXoystsIbW1SR1lIYe+fbsfvbve1JWOU6IUdcpklxVUeqeLi8ci+D24zzXNEV/qOL1KNPTrWtdIeu22Gw27xWS4KaOU2cW/IYqJJScvikJvSmJCzQB/sDaPMQBhxA/GH/Iqdw9aaUh+82T0cxgNroucFdlQnkNupqWqbp0N5r7vpmoCW4eP5ijktM3cUsPOtbMubqbrBfVKGbTBYSpwlyflBqHntSP1FapVU62DgmiIs7qCT0fFEuWolHPaNnLeLXzv9c5mVmzLW3ipFWxod3qv0C1NiG6yhp/+2sFEIMkaD/ZpjWj+dpxzvjlO5YU0o+GIuYjaNmTeWBmq2G+fqDZZ2GY96kUg+pgebhPn2Xgj/9znbtIt5IJfwWp0kFxGEgEBJdkL+35FkL36EaQ2NbOSaLslzbi/dZxwN6NVaDPnHDk/Pr9VrnnmPjrvx+kGClN9qQY/0KOMPTKSa3NefcqPxTlF4/L8e4A3N2pz8nLYWUogTk46f5ByhImoXbHyXmwCiYRNJUq/f3UaVWkNSJQc2fEUPRaqlO3DFdPF3sQTKscAniwQVKxT73dTfJEbNlwNPMJpGCdtejTMqLEoylH4LZAAB+hzZBbBHtY7tq5Z//Gxs35uPrM6ZRhrHrfI+AcZALnaf28UIRsixrV751y8PRBNKjUCU0vxBKxzlYjX9KOa8V/IGxRhtDg+2nV+UqfjsdupZIV+2hFLi39x8oFFgsMEobFYaU2WAskMsp8YEeg9eImdr+a+gAlNqUEoR64Tq0acIMgPqneZhXNdOhDGyaie4ADgLB+kxz+M8PUlM9I3de8ItqJVwf/jdsX/i/rdcL0FM/NBrxOo6B6aNAUvSAijfkwhrKJFQs7INAvrniDPDCBfN1pa8HPDNv1Rn6nB75t1+hoQny9BbxEVK90aVdMbq+auz7ubi2+S99vsn8kuZoylJf3i4SoXXXr9l3w3e91KYi3APZH5a2HS6JVMJnTphbbVKXYviDD8MPfrZ/ZPA5PFI/pz3oBwL7N68PMbkm+j23qUV7Qep17wcq16VX8leTCrxlC8HXtEDS8AkNMZ8Ed18dtzLU6oUf3Yp4YmUoPfYFbN82EU4NguCAMIVz2pHzfXHwy6uyD7zojgRBoflztrj/9197swUIZU4KO2hseI2hq1gMvASHVZLXaXcgHegqQPP0LhHIiVw8W5K/HuMR/CzWPIk6OtBmWXwm3FqZk6Rv83c0cqt8LAlX7Qdwwga6DaugtAheXcQVfqFqXDvDwPBh8caRqkZ/mkef7tKNqMHo5h3VtJ/en5oYF36aW5SKT/kzU6XLMGOTYjmbU2ugo4uUO61e+kU9T3uhrJCGd5q1bu1zYACk5y1bcF1Q/YplRxpF7h5cuTE+r9z2rQ57ETq6XpsT5gdCTZ/5IgSXNpoJmgiu0RuJBsc5mf85naHK9O+qp/uaSHHEt6ngUhw132NLpFjzqXHGvUaE+tOiupkZjMRt40Boea/yAu27LCXK+atGuTHOsc8f1y9SW4a/Nh1TqLIE7EbLFXn4zZSIdV68AHW85tE8kbH2d56fXqNm9EQaYYOmFu8PlDwUKiRHnpmHR559VYeEV7Z/PslVURZ4EJJ4SIx4fRZ5Y6LwSvcQv8zUKBGjvXfygzck9RbUeJh3Y7Lk5sbC1wiaZYGDt99s36G0oCNb5hhTN25C/FJccr0BFU+NBCQlvMfiT9uZu1G3NeRRRUvSH4arW/GW/7HudZn7FCu5p8w31RfLE1oyG1selhx9b1o3bDcT2Br/MTbsuF3S2fPFUkie0Rz6UGtingTf9SMq4zSO+2M1e+R1FWYKR7tCnHuWH0TBZlwtBd+nabwrAjPHludJ4RqDzZWr+axWMmFBOFd9e+acgfmTkmMnU1g8XdB1RMuzqflW8gXRIYWmWXTm+N3MU1W4yfqo2be3OioVjNs8Y3fN5DvT+8Z6TtvrNipCAa5x0s+9oCTre4t6cvXFEoniuixD1yEsNkHQRcMnZFKl1rscgssit2ajlB8p7jGo2/gVcM8KVTzP/VK8lqjvANmYf8cbrwKxKjmqkxOOtTrPF0gbB4ewThbcsAu+oUZTfqmdn7dUJSuThmxIHzlzFRhQ9aK1WkEOy5ScxtfZ2URnoy55fk5D69aSVVzFjPXdMmKKR6PHo5JNyK2P6Vke4KY81+8J8sJiJMjxWbWG/crL3Bkp2Afz2T/9R8MZVJWvCgx/+5rM8M3nc3m5OyJQfYfQDhnPHxVJN8qZVjluOfvZ7tPio04iU28qrgPT5n+z6mkuL6RWSmLqroavyGSn5SH7p5NgsinzvRNs2KHZE7L5FWJJQz/BS9HV7OBfOhV56MAa3ojRkqjni3HtxRRa0BKPfHw96KN2IA8FmKZ9yK1YtD4x+FiJ8tyF3PpNnPhvdM17XNOmAA+1kXexqshc0MbO+tPDzQL9sbzDj5++Leulafv3KNHi+59arRm6M9ohHavP6rkVWwvxZcZz6h/+EeIJexOoqTtcc1sWHKYr8HbAXfZ0/bhR5Au+EizGfiLTwBF2qTRzWxd0UNWZC8GaXpRSPmg8GWUsTaUeoZzS0yN+yP8EgG9R9w8kW9AO7Tb8AM6duVbBiKZmGlH+of/ePFrQc566uxV+p5UV/2Lwbqib35PN6ZOj3kjt3Fg3aH7fBzGsJZf49aki3o0Hs23M5/PzkESWpa4l94I3gV3IXQQiNQBi0IpHN0yMnfJ6tcgKRXrMcj6hUBzdobSd1kMnfYaX7aJjIsD+bqk6X46GlG30q9m+E7/b8TfEBuEHcJJViFryTbcrHO17gbA8D/RPA6dNQg7b0wENtLVU82TtjV6OdjM8GuQFVdvVe1DJpmFapv/yfg9B+Ba4TNFn8YwD1KIbVPzK1C4R34MKYvVoLeu3KXw6nMw6o1+Y84jQ1d+it/BncrJo0eZ/GXYzM6WY/kiX9AHBbweoU9iy5iY4fdxV9NZM5YiTjhuphGXdEVNZaBnn9h19ma04GD77pvp5jOFInF4TapHKU0doPsFVfPQB7Kw/CKH/JnQeg40pUzmh3ctYeOGXK/0G96G+e2z1H4YqqXIBXFFvKW39I3Icjz+BPiPemfz44t0vfaiHV+ncmGFq+rH5kl3Etcod/v0QGJ+Vt5X1kHBvcL+TclpA5J+pIPUSAj9iHuVp3z9Xi86/Ll9itwhec3NBjyy/6IcVa8H/C3A6hY7l5k6+Ny3NL2BWi2yXK6bz+UrvJyfeLoO8gZuRl7/ZuNUa7ObCjLEu+66hfZNfynySqY+BnR9yNHpH4d3pV/TS9tUOa2Igw1dTd8q83JP9wzPCjSWqO8/56029lY5Up7LoD/sYbszduQ1B/Bd8KoE0Se3ZeNHfzAMI/HINjM6k/QUcNZQOK4csILc/Wy/U8fC0VSLdVqHewj/H7dJzrAYsSRDgLR5a5japhUjNC+62sSr032dFl+ytQR6aUTnzNNAKxQEdtfxJdajPTcmnYREFB05YbgOno5dp/beX7PV1661ay3s7kGdbusLuVFlH/26vHHXm97dBjDLDkiMg0i8FLnoH6a0PmgpShHZwrADuH7FiYWxm7Hmvf/HGgFzSHqT4TDABcq9F5yd4rLK6wNoKpK/KnWV0VzA3frXZUfM+0P9kx1NUsBMq7NhUGcjlq/Zf5eZRPHvmqIe8iQUJynK/8MZb/kJ3O6/XBHvhGuNuytXLNeWv5O+4aaxTyMi1FYpEJQaKO8z4t7NsKzzEMqyiWPhlIb72uaJ7Y/F9X22gNfGDm8uZc7Nha1qSO18dF/CU3ebgc91nJ9lEhrdTJHZMfmSIVjgcI1/xEqBiiKKOtLYtn7kPI6fGIlwrlH03soFW0xCX5mAXpJdqJd7vYh/AuWuiuSXYj/hfVn3Sosc3gpOIlX8Y7EE1QhrG2ed026vxXRpaXSwL+7QNX95zODV9+2xIh2Z8ATz9hXsQQsxfzHC1wpSeD9n86BarbCTGC1InxcSM4RdbZZ4D1u/2do/x8aNnnKvcqgGYzV1QvKTnq3URcp8xJCjrWBfjuGXRpTt3GbH79g8LZXkh8OqckrH/r0bjbRK6TTN7y5EKQo4bXwTo4ve6MODiJe0h3qkaP/BhbSfh+ydjfZWCZffqNR0ytoOkc/jW86N96OY1XMrdOcnEyyOZjMeFfNdab+aIeLen4xTnDg2GCaWGA1Te2F2K1GExFbGgjyyvXKOHly5BN0VzP4ELVVXxdxm7gE1cth6rhbzWBIcWo62FNJMRqmymtrdJJOJtKE43uEBRYATCWAinkTlu+OzeGFeerVQVpI23d64Dm/OBOaCgGhNXgpR6Ey7Dg+bU9UbF3kx2DQ6rNFxU2GU0Sw1VTBx58cWYqILHwvcVrq2DSGLGd1L5WuUEtCyo/OhodvyxQB5BVvgylCAaq4H2TIg/9TwvDf2Xv+ZsU8nij7iDOBYAfITysGyVs1GT7GAX7gA32+P8UysCImGsusbq8C09Ax6ykyGXJuSqtrawhJKoSKcdqe8GB9Dyts+UWfckEYqzlvdOBz0LD7s5Ox6Tti3FJBwzOyfVcZ8kC6qNRT9OwAMV92xKVk2FFtFo7tL1nC7H74vToYKZmVq28AsBMP1MYtk2XfXyFdI/z/FFb/V3HcH/DzQvVfhI00T5qmyrOz5nwWUrLuSopnJKU6r2Q7e/P1aHNpvLqYfkpNgt7e2eFVXbdMm64cP02xk5OzDPnnGAmFreiuAv336Q8BNKwFn8314v+aquE/alRfZs1Jobmi0fsoYSZYMSl3+ofMgany+WVOmJScdcE111DMcO3mQksGsBuc1MFTAtuTIX+8zxBkpkpOmPRf0QgbM/+/AFBLBwgmzJ0kN6wAAMSxAABQSwMEFAAIAAgAJLlrQwAAAAAAAAAAAAAAABYAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzSyvNSy7JzM9TSE9P8s/zzMss0dBUqK7lAgBQSwcIRczeXRoAAAAYAAAAUEsDBBQACAAIACS5a0MAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s5VzbctvGGb52nmKHFxk5lag9YAEwkZKRnUmijpVoLNfONE49ILAkYYIAAoAi5aZ3fZTe9wVylzfpk/TfXQAkAYokeJDV1Ja4BLCn//vPi12dfTUdBehWJKkfhect0sYtJEI38vywf94aZ70Tu/XVl5+c9UXUF93EQb0oGTnZecto09asHVy1uSUb+955q9frYdHD3RPR8zonRrdnnjjUpicWd1nP7jkGZlATTVP/8zD63hmJNHZcceMOxMh5EblOpvocZFn8+enpZDJpF6O3o6R/2u9329PUayGYeZiet/Ivn0N3C40mTFWnGJPTH69e6O5P/DDNnNAVLSSpGvtffvLkbOKHXjRBE9/LBoAB6dgtNBB+fwB02iZM9VTWioHYWLiZfytSaDt3qYjORnFLVXNC+fyJ/oaCkp4W8vxb3xPJeQu3qWXSDrMpw8xmHYuxFooSX4RZXpnkg54W3Z3d+mKi+5Xf1JBGC2VRFHQd2SX69VdEMcXoWBZEFxQK09SPsL6HmS6oLgxdcF3H0M0NXdXQdQxdx4A53vqp3w0EsNgJUsDQD3sJ8K+8TrO7QKj55Ddm5JNjoCn1P0BlhgFTDTrcx/hY/prwa+Ac7DkiydyoWTJeOah+PjdmMSIhdoMh6U6EspJMRupjUr58THuOl0Ty6ldEJJNUwZBkD1FskoWRX5r60lIFwbog+UNbfnTkhbkb40oQ+RyGQIb6Ub91pq0aUnNpzyOyVUyrjni/nMwPeNI5Zp1jYhL7mBCrPqRpPDSRBu5YeyeTmFIw4QPuHncIq40qSV9iZ3RJ8nL/8C+B4uy0sIJn+YRQOpB1c8OQiVEqp8g6iCvJJ4iDKpkWGDCOSAcKS6oURYQjg8MlsZEpSwsxqUUGYshGsh5hSNk9bsOHYanOTMShM3nX0rqGmIE4Q0SZSwMBDkiZXECFMqjBOeLQSA5PqOyCmcgw4YrZyIA5SmtrSVVn0BCuYXiKGEFMNiYWoiYyZX/EkFbctOXUoUuKTIxMhTwYbDDW2lBDfRsxSQ1oXxylfonuQARxAZLC0Q/jcbaAnTvyiq9ZFJc8VLW9yB0+K7HOnwgnzeargauaeUTtuhYc5pOzwOmKAOKKGykICN06gTSWaoReFGaoEAJb3+snTjzw3fRGZBm0StF759Z54WRi+g3UToux1dDKkZ+JsRv4nu+Er0FKZBeyQzTz69IHFH7dtEw9jBtFiXdzl4LsoOlfRRKdtzq8zQ2DmgaItYktDnDe6SeMmG1K4BZ82AbD8CR1HSnznLcxYYYNoQ2HZ1If7pY/AkulBha3JWXOVJT0oH7il6yQ3y/TZ1HglY/jyA+z506cjRMVowFNiSTpIuwHQkGrHBhEO+6wG01vNKZM9/XqLhayiZpAt/88CqIEgUZSzqFCXnZ1qerImZW1sKqDVQ1cMMn3yuekQ1UNVXZ1qWoB1/XUckpJQSXBxTB+qmwNdL4gZUpmZOw0Dv3sRXGR+e4wJ5XoBt+PR10Qtxy3xT7Jvvo8O61I2NlQJKEItBiFwMtxNE61YJfC+eRsnIprJxtchN5L0QeVvHakWcyga111NmVPuP4IGur7OXiOZOxfYKr6rif6iShIDFRYrKFVT/G8UNduq66+SaLRZXj7CqSmNlWIjROQJJiEtB2L0zs7Lag9S93Ej6Xooi5Y8aGYSafnpw74AG9eOwGaFDpxVZeZn0mIv3ZS9MZJU5F0xeD3fwWAxijyRBCg3u+/JcgTIbocxeMgbSFnnA0ikC7AMAEeoe+BtJEThugodQfjIB7cpf5w4g/9tieewgzAQkjRQzciBp0GDoJZBvmX9iEQIwixUaa0QClSKQ3PVfAu2Y6i7nuwWlVxmXEJni9VCaU8DkzIkRF+Dnng3MEM5vmp+rsCYiusKUAHSxRrGYyF0OKrJwxfYuhOaf0czxSvUzSFgAW3O5wTiFh4h1kYUi5Q+zu4b7QxI9xgpkktG5s2mK0POtnTmY1EQhqKBZus71ZkCFRAg1iDMxyPBPCnxOtKcleBCq3HeR+0GHIB6Dwe2BRnPIcyqaGM51D+oddLRaagoRoJeykP8l7SQKZnaORrrzlypirHyv0Hk+ntVMGGwZZ3IEuybWpa2NBd83anY5gd2wa/wZgpA9KePxWlLQch9j+AlVhU+ZlpzMDZDSHZS3Vil1tq9eU73wONKOe5gazgZbKywLxpnMBYspMc+G4iIIB6F4Brn0KnDH2G0l+S7Egx8qn28atZXvZQ4brRpsqbmrYFyTW1zYb8XT3v51f5jJ+jP6Ej3OYw8WImxwhS7fkbT1uL2l8nqmIWrrazC6atCJJFVxfbGoaZepM2AQWWYgc/HQaRiRY82u5Y2LaZ0YE4Htsm3492LwH6ukD6SkF9jMDikOaQXj8Apmw3TEHZD4HpSvX5VoBDk9mP3x+CtFa1iH1s28k3tZ04t528tJ08t51Y2k5qG9iCT2IyTA2rcFFgPTsGmFVsMAr+iz+Y+QSTsRcDGpe2s8JJsD/aG25gQ+O6+TQLxm9nMFcO51UHw0ulrGkohFfqJt5UkEDkSklyumkUjDNx40L4G86WibV0FDkexrmkGUTJHIiWySWAhTDllDSQJvoAznglj2qWYP88Wm0KNlJ2uU6+EY/skkfczlnEOd2JRY0VHs+4hJeF13MZ34ZMelllEn9MTNpBkRjOmUQ5/t/Wo4pVfvf3l8IdZOk/6uHqw3JuztMyo2GaghvylZZ8NZlZGEhmPKz2beVu1yeb9zJ0edb5IAwlGuITa4u8c2uGWsR6SIZuqqkQdzvxbF3pVeIE8H99XDXMoyqCTtFLiKV0RgoZyCLXn8Lj/NFn1UebRF7DupuldYmgMt0HqjhZHuisJuU1MBQerg4TgbL7TFWNsk0IKwatkEeM3eLKGnE37iBxwqHIqcuHnXGlxrBNJl92WsuG+F4n7+azLsZDJ1UmbDJbty5DDaa5gQAN8mkOjrKn6BzNzdYF2YBHRydD+JItxbY3DtUibGvW2xqrOKe7+wz18bbGZzU4kxyciQYHjC9AoZBakYDVQJkcHJSV6z3NY6d5UNxoNHJCD4Xqxeu1WniZvfBz8HlrejH103z246y4e6E7ypuvWcG52G79hlD9kkmVG6yXr5SdfayXF5GtKg+yZHZBcpE8mh5dPD1Gd/AJdpA3XTODfrZbMtPOShZdXWyLdx01fjjU6Dxqhd/Q6DVGjj4e5Ojh5Y3djxxceY3RY/9X6Bkr0WuutcbjQ+9wWjsotHZAtf89KiLAkwUnLOP09UFsPVZZq8gfIVjZ0i9f9lrQd1Is7c2cs8Lp0372BVIgwmxJ8SYVObSW51a9eDdxxulqT17DVbfZL7SbrlQdANob0Zf3K7hKPyyhvKhB5qyGK827K4Bw6kgtvIE5kAzmWpnC5BT3LoIgmgivtn9jpu+8Yi1nY22R8YtfQt0k1Rtk/FEc+C6kRAWagYyyLkO5p0VPsL4LZihELLcf/RBC4h+mch95dfvLwvLA7VZ8NnI+s7puNGN09+MwGu/MaMh6Hj2rN1/Ye1bsDroIPziD2quxTVb2DmS7DroX4809iYP0D02jkDePMXlgBwtD3ixkD1RjR7cH7xHmD/sCr7pYENz1o7BqUXODSnUAotB1mJaqqol97UuzNcx9rfOO6DZO3mSivhjyC1m33KCnUq5gFh1vFy3saMcX1ykob8a+Nab8flNYCz3erdXjxsQczi2Vbw03ij/WsO8jO6UaJ/aRijwUI05YJUAw/0CcmCxjxW76fXiVOKF/SE4ssU4bbE4rTh40DZln71gLUPeUOFXVZbXh4o+ASesSp3qMdJlHSJd6oeZrCLlvHXlO56fBz43elVzuvmv+kSzJ3JNPltFPNdYZNUsnR1sph8aJ4J1fKh3Mca+R/wOYoUW2fVNK5NL1tMr70f/8899/y1+Qwq+Zr69hHaYWZ5HmmDxwwg8Nl9NUk41dkhuFnq+zR6j+Q147qkuC3G4w23Ww00mTpXy0Cj7SZmqzBv/FJWCF+apl4DXcoFuwg/7R+bEIQDeKAuHM6I+qKybzh70OZ7bnCZ55aoNw/Q7CXn3iIT+6uLD/u+7nXoskcMY9BAwWfl+E691e/C5ZvvNmt/01stsKyvaet9a8EtOsWBH69JdxlH3xFmykPiGH3qIYnLi+Lc9lvHBeiR9/it8FP8tVj/z+22P03V1+sYyoDEZoLQ538MB6N5flp4rQaiykjhKnwKBeefDc/yCu8r9too8Y41YRkBXrA/Lco9otgXIfaBgms21sUIYt3qG2DjJxW/65Dk5tym3bsCxz4STdOukj+zgeQPZ8PGDJPOk+5kkPeYzBHzn9mSg+8wNPD9fzwYxqz2Q5PU44sTuEdT3TJpZnMJNx28C25+Euf3sxzqJ3XTAh7fdxPxep8JnjDvtJNA7r8jYnI6E6GaxmrM9D3Vtjbhn3udTG2cG0O7jxdL+L16Spjm2/k7PJqlZ9F+TCMbKKlB0j3HSR9vXjOaNnVM6TkUMe0VsMxV4D4VFSCcDk4UgZVb2uRVO3qyOpW91bgeDtwZP7+QN7s5DBWpXcN09uILlf/GfsL9efO3OfOxcXzIFIfSesmYdc/NerynWpKtdSV2J1pLWpfjzEecsN9cNarh+HOW65kX5cawW5rilI3EhB4h0S/ObRUnX1i+5LQcx9rn5toRHXTf0+q/r9Lu90u8wjwsEdaroeNXomYQZ3PYtbvY6l/X4/+f23sP3n628fj+PffnvBMr+/6+bZ3f3+6fzf/ZDXxV/x+/K/UEsHCEGIaPT4DQAAdVAAAFBLAQIUABQACAAIACS5a0OMx+dMK58AAC+pAAAuAAAAAAAAAAAAAAAAAAAAAAA3YWY1MTUxODkxM2JkNjgxN2Q0MzYzNTg0MDhkZDBiNVxBdXRvX2JsYXUuanBnUEsBAhQAFAAIAAgAJLlrQybMnSQ3rAAAxLEAAC8AAAAAAAAAAAAAAAAAh58AAGI1OWJiM2QxZWEwOTI2Y2QyNGY2MTM0NWNkNzU3Zjk3XEF1dG9fZ3LDvG4uSlBHUEsBAhQAFAAIAAgAJLlrQ0XM3l0aAAAAGAAAABYAAAAAAAAAAAAAAAAAG0wBAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgACAAkuWtDQYho9PgNAAB1UAAADAAAAAAAAAAAAAAAAAB5TAEAZ2VvZ2VicmEueG1sUEsFBgAAAAAEAAQANwEAAKtaAQAAAA==" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "false" />
| + | |
| | + | {{#widget:Iframe |
| | + | |url=https://www.geogebra.org/material/iframe/id/jGJRWYCw/width/1325/height/666/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/true/rc/false/ld/false/sdz/false/ctl/false |
| | + | |width=1000 |
| | + | |height=500 |
| | + | |border=0 |
| | + | }} |
| | + | |
| | + | ====Bewegung als Translation und Rotation==== |
| | + | *Die Bewegung eines Körpers kann man als eine Überlagerung einer Translation im Raum und eine Drehung in sich beschreiben. |
| | + | |
| | + | *Die Bewegung wird durch die Menge an Impuls <math>\vec p</math> (Schwung) für die Translation und Drehimpuls <math>\vec L</math> (Drehschwung) für die Rotation angegeben. |
| | + | |
| | + | *Sowohl Impuls als auch Drehimpuls haben eine Richtung und sind vektorielle Größen. Sie geben an, wieviel Schwung, bzw. Drehschwung ein Gegenstand hat, also wieviel "Bewegungsmenge" in dem Körper steckt. Außerdem gibt er an in welche Richtung er sich bewegt, bzw. um welche Achse er sich dreht. |
| | + | |
| | + | *In der Schulphysik betrachtet man in der Regel Bewegungen von Gegenständen, bei denen die Drehbewegung keine Rolle spielt und beschreibt nur die Translation. |
| | | | |
| | ==Trägheitsgesetz (1. Newtonsches Axiom)== | | ==Trägheitsgesetz (1. Newtonsches Axiom)== |
| Zeile 69: |
Zeile 82: |
| | | | |
| | ==Veränderungsgesetz (2. Newtonsches Axiom)== | | ==Veränderungsgesetz (2. Newtonsches Axiom)== |
| − | [[Image:Mechanik_Änderung_Bewegungszustand.jpg|thumb|Eine Veränderung der Bewegungsmenge durch eine Kraft. Der Wagen wird langsamer.]] | + | [[Image:Mechanik_Änderung_Bewegungszustand.jpg|thumb|Eine Veränderung der Bewegungsmenge durch eine Kraft. Der Impuls des Wagens nimmt ab.]] |
| | | | |
| | {|class="wikitable" | | {|class="wikitable" |
| | |style="border-style: solid; border-width: 4px "| | | |style="border-style: solid; border-width: 4px "| |
| − | Drückt (zieht) man mit einer Kraft <math>\vec F</math> an einem Gegenstand, | + | Drückt (zieht) man mit einer [[Die Kraft|Kraft]] <math>\vec F</math> an einem Gegenstand, |
| | <br> so wird die Richtung oder die Menge des Impulses <math>\vec p</math> verändert. | | <br> so wird die Richtung oder die Menge des Impulses <math>\vec p</math> verändert. |
| | | | |
| Zeile 79: |
Zeile 92: |
| | <br> so wird die Richtung oder die Menge des Drehimpulses <math>\vec L</math> verändert. | | <br> so wird die Richtung oder die Menge des Drehimpulses <math>\vec L</math> verändert. |
| | |} | | |} |
| | + | |
| | + | ==Aufgaben== |
| | + | ;1) Berechne jeweils die Impulsmenge |
| | + | :a) Ein Vogel mit der Masse 100 g fliegt mit 36 km/h. |
| | + | :b) Ein Fußgänger (m=72 kg) läuft mit 5 km/h. |
| | + | :c) Ein Auto (m=1 t) fährt mit 36 km/h. |
| | + | |
| | + | ;2) Anke und ihr Papa fahren zusammen Rad. |
| | + | :Anke wiegt 40 kg, ihr Vater 90 kg, jedes ihrer Räder 10kg. Sie fahren mit 18 km/h nebeneinander. |
| | + | :a) Wieviel Impuls steckt in Anna, in ihrem Vater und wieviel in den beiden Rädern? |
| | + | :Stelle dies mit dem Wasserbehältermodell dar. |
| | + | :b) Wie schnell muss Anke fahren, um genausoviel Impuls wie ihr Vater zu haben? (mit Rädern) |
| | + | :Stelle auch dies im Wasserbehältermodell dar. |
| | + | |
| | + | ;3) Ball und Gewehrkugel |
| | + | :Ein Tennisball (m=57g) kann bei einer Geschwindigkeit von 5 km/h einen Holzklotz umschmeißen. |
| | + | :Wie schnell muß dazu eine Luftgewehrkugel sein, wenn sie nur 0,541 g Masse hat? |
| | + | |
| | + | ===[[Aufgaben zum Impuls als Bewegungsmenge - Lösungen|Lösungen]]=== |
| | | | |
| | ==Links== | | ==Links== |
| − | *[https://www.univie.ac.at/physikwiki/index.php/LV001:LV-Uebersicht/Videos/Rollende_Zylinder Video] von herabrollender Dose und Zylinder. (Fakultät für Physik Uni Wien; eLearning) | + | *[https://www.univie.ac.at/physikwiki/index.php/LV001:LV-Uebersicht/Videos/Rollende_Zylinder Video] von herabrollender Dose und Zylinder. (Fakultät für Physik Uni Wien; eLearning) Probleme mit Flash-Player |
| | + | *[https://www.youtube.com/watch?v=hebr1xH-Wsw Video] von herabrollenden Zylindern mit unterschiedlicher Messeverteilung. (youtube: "Versuch auf schiefer Ebene - Versuch" von "Noob Physik") |
| | *[http://www.youtube.com/watch?v=4OD4aDlAiZI Video] der Drehschwingung eines Menschen auf einem Drehstuhl. (youtube: "Trägheitsmomente" von "Wissenschaftskanal1") | | *[http://www.youtube.com/watch?v=4OD4aDlAiZI Video] der Drehschwingung eines Menschen auf einem Drehstuhl. (youtube: "Trägheitsmomente" von "Wissenschaftskanal1") |
| − |
| |
| | | | |
| | ==Fußnoten== | | ==Fußnoten== |
| | <references /> | | <references /> |
Weitere Beispiele sind der Luftkissenpuck (Fußball), ein Mensch auf einem Bürodrehstuhl oder Experimente am Luftkissentisch oder -bahn.
Mit Hilfe der Regler kann man die Masse und die Geschwindigkeit des Autos verändern. (Die Massen- und Geschwindigkeitsangaben sind in kg und in m/s und deshalb etwas ;) unrealistisch.)