Aufgaben zum Impuls als Bewegungsmenge (Lösungen): Unterschied zwischen den Versionen
Aus Schulphysikwiki
(→3) Ball und Gewehrkugel) |
|||
| (9 dazwischenliegende Versionen des gleichen Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | *[[Aufgaben zum Impuls als Bewegungsmenge|'''Zurück zu den Aufgaben''']] | |
| + | |||
| + | ====1) Impulsmengen berechnen==== | ||
| + | Berechne jeweils die Impulsmenge | ||
:a) Ein Vogel mit der Masse 100 g fliegt mit 36 km/h. | :a) Ein Vogel mit der Masse 100 g fliegt mit 36 km/h. | ||
:Um die Impulsmenge in Huygens berechnen zu können, muss man zunächst die Masse in kg und die Geschwindigkeit in m/s angeben: | :Um die Impulsmenge in Huygens berechnen zu können, muss man zunächst die Masse in kg und die Geschwindigkeit in m/s angeben: | ||
| Zeile 10: | Zeile 13: | ||
::<math>p = m\, v = \mathrm{1000\, kg \cdot 10\frac{m}{s} = 10000\, Hy} </math> | ::<math>p = m\, v = \mathrm{1000\, kg \cdot 10\frac{m}{s} = 10000\, Hy} </math> | ||
| − | + | ====2) Bewegungsmenge im Wasserbehältermodell==== | |
| − | + | Anke und ihr Papa fahren zusammen Rad. Anke wiegt 40 kg, ihr Vater 90 kg, jedes ihrer Räder 10kg. Sie fahren mit 18 km/h nebeneinander. | |
:a) Wieviel Impuls steckt in Anna, in ihrem Vater und wieviel in den beiden Rädern? | :a) Wieviel Impuls steckt in Anna, in ihrem Vater und wieviel in den beiden Rädern? | ||
:Stelle dies mit dem Wasserbehältermodell dar. | :Stelle dies mit dem Wasserbehältermodell dar. | ||
| − | :b) Wie schnell muss Anke fahren, um | + | :Umrechnen der Geschwindigkeit: |
| + | ::<math>18\rm\frac{km}{h}= 18\frac{1000\,m}{3600\,s}=5\frac{m}{s} </math> | ||
| + | Damit kann man zwei Wasserbehälter für Anke und ihren Vater zeichnen: | ||
| + | :{| | ||
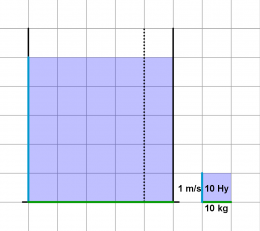
| + | |[[Datei:Wasserbehältermodell Aufgabe Anke Fahrrad.png|thumb|260px|none|Weil Anke und ihr Fahrrad gemeinsam fahren, reicht ein Behälter zur Darstellung. Die gestrichelte Linie trennt Anke mit der Masse von 40kg von ihrem Fahrrad mit 10kg ab.]] | ||
| + | | | ||
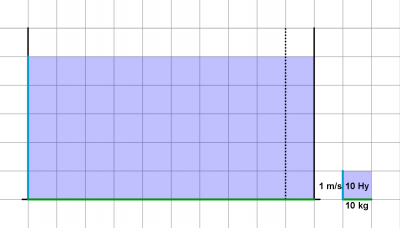
| + | [[Datei:Wasserbehältermodell Aufgabe Anke Fahrrad Vater.png|thumb|400px|none|Ankes Vater hat eine größere Masse, also hat der Behälter einen größeren Boden. Weil Anke und ihr Vater gleich schnell sind, steht das Wasser auch gleich hoch.]] | ||
| + | |} | ||
| + | |||
| + | Berechnung der Impulsmengen: | ||
| + | {| | ||
| + | |style="text-align:right"| | ||
| + | :Anke: | ||
| + | | | ||
| + | <math>p = m\, v = \mathrm{40\, kg \cdot 5\frac{m}{s} = 200\, Hy} </math> | ||
| + | |- | ||
| + | |style="text-align:right"| | ||
| + | :Vater: | ||
| + | | | ||
| + | <math>p = m\, v = \mathrm{90\, kg \cdot 5\frac{m}{s} = 450\, Hy} </math> | ||
| + | |- | ||
| + | |style="text-align:right"| | ||
| + | :ein Rad: | ||
| + | | | ||
| + | <math>p = m\, v = \mathrm{10\, kg \cdot 5\frac{m}{s} = 50\, Hy} </math> | ||
| + | |} | ||
| + | |||
| + | :b) Wie schnell muss Anke fahren, um genauso viel Impuls wie ihr Vater zu haben? (mit Rädern) | ||
:Stelle auch dies im Wasserbehältermodell dar. | :Stelle auch dies im Wasserbehältermodell dar. | ||
| + | Anke hat zusammen mit ihrem Rad nur eine Masse von 50 kg. Deshalb muss sie schneller fahren als ihr Vater, um den gleichen Impuls zu haben. Ihr Papa hat zusammen mit seinem Rad eine Masse von 100kg. | ||
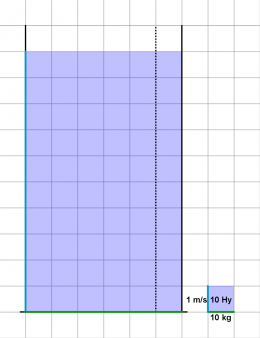
| + | :[[Datei:Wasserbehältermodell_Aufgabe_Anke_Fahrrad_schnell.png|thumb|260px|none|Im Wasserbehältermodell ist schnell klar, wie hoch das Wasser stehen muss.]] | ||
| − | + | Ein einfacher rechnerischer Lösungsweg sieht so aus: | |
| − | :Ein | + | <br>Zuerst berechnet man die Impulsmenge von Ankes Vater mit Fahrrad: |
| + | :<math>p_{Vater}= 450\,\rm Hy + 50\,\rm Hy = 500\,\rm Hy</math> | ||
| + | Anke soll mit Rad nun genausoviel Impuls haben wie ihr Vater. Der Impuls berechnet sich als Masse mal Geschwindigkeit: | ||
| + | :<math>50\,{\rm kg} \cdot v =500\,\rm Hy</math> | ||
| + | Teilt man die Gleichung durch die Masse, erhält man die Geschwindigkeit: | ||
| + | :<math> | ||
| + | \begin{alignat}{2} | ||
| + | 50\,{\rm kg} \cdot v &=500\,\rm Hy & \quad | :50\,{\rm kg} \\ | ||
| + | \Rightarrow \quad v &= 10\,\rm \frac{m}{s} = 36 \rm \frac{km}{h} | ||
| + | \end{alignat} | ||
| + | </math> | ||
| + | |||
| + | Dieses Ergebnis überrascht nicht wirklich, das hätte man sich auch anders überlegen können: Weil Anke nur die halbe Masse hat, muss sie doppelt so schnell fahren, um 500 Huygens Impuls zu haben: | ||
| + | ::<math>p = m\, v \quad \Rightarrow \quad v = \frac{p}{m} = \frac{500\,\rm Hy}{50\,\rm kg} = 10\,\rm \frac{m}{s}=36\,\rm\frac{km}{h}</math> | ||
| + | |||
| + | ====3) Ball und Gewehrkugel==== | ||
| + | :Ein Tennisball (m=57g) kann bei einer Geschwindigkeit von 5 km/h einen Holzklotz umschmeißen. | ||
:Wie schnell muß dazu eine Luftgewehrkugel sein, wenn sie nur 0,541 g Masse hat? | :Wie schnell muß dazu eine Luftgewehrkugel sein, wenn sie nur 0,541 g Masse hat? | ||
| + | :Zuerst berechnet man den Impuls, der in dem Tennisball enthalten ist: | ||
| + | ::<math>\mathrm{57\,g=0{,}057\, kg \qquad 5\frac{km}{h}= 5\frac{1000\,m}{3600\,s}\approx 1{,}39\rm \frac{m}{s}}</math> | ||
| + | ::<math>p_{Ball}= 0{,}057\, kg \cdot 1{,}39\rm \frac{m}{s} \approx 0{,}079\,\rm Hy</math> | ||
| + | :Die Luftgewehrkugel soll den gleichen Impuls haben wie der Ball. Dann teilt man die Gleichung durch die Masse der Gewehrkugel: | ||
| + | ::<math> | ||
| + | \begin{alignat}{2} | ||
| + | m_{Kugel}\cdot v_{Kugel} &= 0{,}079\,\rm Hy \\ | ||
| + | 0,000541 \,{\rm kg} \cdot v_{Kugel} &= 0{,}079\,\rm Hy & \quad | :0,000541 \,\rm kg \\ | ||
| + | \Rightarrow \quad v_{Kugel} &\approx 146\,\rm \frac{m}{s} \approx 536 \rm \frac{km}{h} | ||
| + | \end{alignat} | ||
| + | </math> | ||
| + | :Das ist ganz schön schnell, immerhin die halbe Schallgeschwindigkeit! | ||
| + | |||
| + | :Ein zweiter Lösungsweg verlangt etwas mehr mathematische Kenntnisse: | ||
| + | :Der Ansatz ist der gleiche, Ball und Kugel sollen den gleichen Impuls haben. | ||
| + | :Dann löst man nach der Kugel-Geschwindigkeit auf, indem man die Gleichung durch die Masse der Kugel teilt: | ||
| + | ::<math> | ||
| + | \begin{alignat}{2} | ||
| + | m_{Kugel}\cdot v_{Kugel} &= m_{Ball}\cdot v_{Ball}& \quad | :m_{Kugel} \\ | ||
| + | \Rightarrow \quad v_{Kugel} &= \frac{m_{Ball}}{m_{Kugel}}\cdot v_{Ball}\\ | ||
| + | \end{alignat} | ||
| + | </math> | ||
| + | :Nachdem die Gleichung passend umgestellt ist, kann man nun die Werte einsetzen. In diesem Fall muss man die Masse nicht unbedingt in kg umrechnen, weil sich die Einheit der Masse wegkürzt: | ||
| + | ::<math>v_{Kugel} = \frac{57\,\rm g\!\!\! /}{0{,}541\,\rm g\!\!\! /} \cdot 5\,\rm\frac{km}{h} \approx 105 \cdot 5\,\rm\frac{km}{h} = 525\,\rm\frac{km}{h}</math> | ||
| + | :Man erhält natürlich in etwa das gleiche Ergebnis. Wegen der unterschiedlichen Rundungen stimmt es nicht exakt überein. | ||
Aktuelle Version vom 12. Mai 2019, 20:45 Uhr
1) Impulsmengen berechnen
Berechne jeweils die Impulsmenge
- a) Ein Vogel mit der Masse 100 g fliegt mit 36 km/h.
- Um die Impulsmenge in Huygens berechnen zu können, muss man zunächst die Masse in kg und die Geschwindigkeit in m/s angeben:
- [math]\mathrm{100\,g=0{,}1\, kg \qquad 36\frac{km}{h}= 36\frac{1000\,m}{3600\,s}=10\frac{m}{s}} [/math]
- [math]p = m\, v = \mathrm{0{,}1\, kg \cdot 10\frac{m}{s} = 1\, Hy} [/math]
- b) Ein Fußgänger (m=72 kg) läuft mit 5 km/h.
- [math]p = m\, v = \mathrm{72\, kg \cdot 1{,}39\frac{m}{s} = 100\, Hy} [/math]
- c) Ein Auto (m=1 t) fährt mit 36 km/h.
- [math]p = m\, v = \mathrm{1000\, kg \cdot 10\frac{m}{s} = 10000\, Hy} [/math]
2) Bewegungsmenge im Wasserbehältermodell
Anke und ihr Papa fahren zusammen Rad. Anke wiegt 40 kg, ihr Vater 90 kg, jedes ihrer Räder 10kg. Sie fahren mit 18 km/h nebeneinander.
- a) Wieviel Impuls steckt in Anna, in ihrem Vater und wieviel in den beiden Rädern?
- Stelle dies mit dem Wasserbehältermodell dar.
- Umrechnen der Geschwindigkeit:
- [math]18\rm\frac{km}{h}= 18\frac{1000\,m}{3600\,s}=5\frac{m}{s} [/math]
Damit kann man zwei Wasserbehälter für Anke und ihren Vater zeichnen:
Weil Anke und ihr Fahrrad gemeinsam fahren, reicht ein Behälter zur Darstellung. Die gestrichelte Linie trennt Anke mit der Masse von 40kg von ihrem Fahrrad mit 10kg ab.
Ankes Vater hat eine größere Masse, also hat der Behälter einen größeren Boden. Weil Anke und ihr Vater gleich schnell sind, steht das Wasser auch gleich hoch.
Berechnung der Impulsmengen:
|
[math]p = m\, v = \mathrm{40\, kg \cdot 5\frac{m}{s} = 200\, Hy} [/math] |
|
[math]p = m\, v = \mathrm{90\, kg \cdot 5\frac{m}{s} = 450\, Hy} [/math] |
|
[math]p = m\, v = \mathrm{10\, kg \cdot 5\frac{m}{s} = 50\, Hy} [/math] |
- b) Wie schnell muss Anke fahren, um genauso viel Impuls wie ihr Vater zu haben? (mit Rädern)
- Stelle auch dies im Wasserbehältermodell dar.
Anke hat zusammen mit ihrem Rad nur eine Masse von 50 kg. Deshalb muss sie schneller fahren als ihr Vater, um den gleichen Impuls zu haben. Ihr Papa hat zusammen mit seinem Rad eine Masse von 100kg.
Im Wasserbehältermodell ist schnell klar, wie hoch das Wasser stehen muss.
Ein einfacher rechnerischer Lösungsweg sieht so aus:
Zuerst berechnet man die Impulsmenge von Ankes Vater mit Fahrrad:
- [math]p_{Vater}= 450\,\rm Hy + 50\,\rm Hy = 500\,\rm Hy[/math]
Anke soll mit Rad nun genausoviel Impuls haben wie ihr Vater. Der Impuls berechnet sich als Masse mal Geschwindigkeit:
- [math]50\,{\rm kg} \cdot v =500\,\rm Hy[/math]
Teilt man die Gleichung durch die Masse, erhält man die Geschwindigkeit:
- [math] \begin{alignat}{2} 50\,{\rm kg} \cdot v &=500\,\rm Hy & \quad | :50\,{\rm kg} \\ \Rightarrow \quad v &= 10\,\rm \frac{m}{s} = 36 \rm \frac{km}{h} \end{alignat} [/math]
Dieses Ergebnis überrascht nicht wirklich, das hätte man sich auch anders überlegen können: Weil Anke nur die halbe Masse hat, muss sie doppelt so schnell fahren, um 500 Huygens Impuls zu haben:
- [math]p = m\, v \quad \Rightarrow \quad v = \frac{p}{m} = \frac{500\,\rm Hy}{50\,\rm kg} = 10\,\rm \frac{m}{s}=36\,\rm\frac{km}{h}[/math]
3) Ball und Gewehrkugel
- Ein Tennisball (m=57g) kann bei einer Geschwindigkeit von 5 km/h einen Holzklotz umschmeißen.
- Wie schnell muß dazu eine Luftgewehrkugel sein, wenn sie nur 0,541 g Masse hat?
- Zuerst berechnet man den Impuls, der in dem Tennisball enthalten ist:
- [math]\mathrm{57\,g=0{,}057\, kg \qquad 5\frac{km}{h}= 5\frac{1000\,m}{3600\,s}\approx 1{,}39\rm \frac{m}{s}}[/math]
- [math]p_{Ball}= 0{,}057\, kg \cdot 1{,}39\rm \frac{m}{s} \approx 0{,}079\,\rm Hy[/math]
- Die Luftgewehrkugel soll den gleichen Impuls haben wie der Ball. Dann teilt man die Gleichung durch die Masse der Gewehrkugel:
- [math] \begin{alignat}{2} m_{Kugel}\cdot v_{Kugel} &= 0{,}079\,\rm Hy \\ 0,000541 \,{\rm kg} \cdot v_{Kugel} &= 0{,}079\,\rm Hy & \quad | :0,000541 \,\rm kg \\ \Rightarrow \quad v_{Kugel} &\approx 146\,\rm \frac{m}{s} \approx 536 \rm \frac{km}{h} \end{alignat} [/math]
- Das ist ganz schön schnell, immerhin die halbe Schallgeschwindigkeit!
- Ein zweiter Lösungsweg verlangt etwas mehr mathematische Kenntnisse:
- Der Ansatz ist der gleiche, Ball und Kugel sollen den gleichen Impuls haben.
- Dann löst man nach der Kugel-Geschwindigkeit auf, indem man die Gleichung durch die Masse der Kugel teilt:
- [math] \begin{alignat}{2} m_{Kugel}\cdot v_{Kugel} &= m_{Ball}\cdot v_{Ball}& \quad | :m_{Kugel} \\ \Rightarrow \quad v_{Kugel} &= \frac{m_{Ball}}{m_{Kugel}}\cdot v_{Ball}\\ \end{alignat} [/math]
- Nachdem die Gleichung passend umgestellt ist, kann man nun die Werte einsetzen. In diesem Fall muss man die Masse nicht unbedingt in kg umrechnen, weil sich die Einheit der Masse wegkürzt:
- [math]v_{Kugel} = \frac{57\,\rm g\!\!\! /}{0{,}541\,\rm g\!\!\! /} \cdot 5\,\rm\frac{km}{h} \approx 105 \cdot 5\,\rm\frac{km}{h} = 525\,\rm\frac{km}{h}[/math]
- Man erhält natürlich in etwa das gleiche Ergebnis. Wegen der unterschiedlichen Rundungen stimmt es nicht exakt überein.
