*: Unterschied zwischen den Versionen
(→Leere Seite) |
|||
| Zeile 6: | Zeile 6: | ||
|} | |} | ||
__NOTOC__ | __NOTOC__ | ||
| + | ==Aufgaben zur Impulsmenge und zum 2. Newtonschen Gesetz== | ||
| + | ====1) Impulsmengen berechnen==== | ||
| + | [[Datei:Möve_fliegend.jpg|thumb|140px]] | ||
| + | Berechne jeweils die Impulsmenge: | ||
| + | :a) Ein Vogel mit der Masse 100 g fliegt mit 36 km/h. | ||
| + | :b) Ein Fußgänger (m=72 kg) läuft mit 5 km/h. | ||
| + | :c) Ein Auto (m=1 t) fährt mit 36 km/h. | ||
| − | == | + | ====2) Bewegungsmenge im Wasserbehältermodell==== |
| − | = | + | Anke und ihr Papa fahren zusammen Rad. Anke wiegt 40 kg, ihr Vater 90 kg, jedes ihrer Räder 10kg. Sie fahren mit 18 km/h nebeneinander. |
| − | + | :a) Wieviel Impuls steckt in Anna, in ihrem Vater und wieviel in den beiden Rädern? | |
| − | + | :Stelle dies mit dem Wasserbehältermodell dar. | |
| + | :b) Wie schnell muss Anke fahren, um genausoviel Impuls wie ihr Vater zu haben? (mit Rädern) | ||
| + | :Stelle auch dies im Wasserbehältermodell dar. | ||
| − | === | + | ====3) Ball und Gewehrkugel==== |
| − | + | Ein Tennisball (m=57g) kann bei einer Geschwindigkeit von 5 km/h einen Holzklotz umschmeißen. | |
| − | + | :Wie schnell muß dazu eine Luftgewehrkugel sein, wenn sie nur 0,541 g Masse hat? | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | ===4 | + | ====4) Das Wasserbehältermodell I==== |
| − | + | *In der Tabelle ist außer der ersten Spalte einiges durcheinandergeraten. Sortiere es wieder richtig. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | {|class="wikitable" | |
| − | + | !Bewegung | |
| + | !Wasserbehälter | ||
| + | |- | ||
| + | || Impulsmenge || Grundfläche | ||
| + | |- | ||
| + | || Masse || Wassermenge | ||
| + | |- | ||
| + | || Geschwindigkeit || Abflussrate | ||
| + | |- | ||
| + | || Kraft || Zuflussrate | ||
| + | |- | ||
| + | || Reibungskraft || Wasserhöhe | ||
| + | |} | ||
| − | ===5 | + | ====5) Jemanden anschieben==== |
| − | + | Moritz wird von Karla wird auf einem Bürodrehstuhl angeschoben. Seine (träge) Masse beträgt 70kg und die des Stuhls 10kg. Dabei wird er 2 m/sec schnell. | |
| − | + | *Wieviel Impuls steckt in Moritz und wieviel im Stuhl? | |
| − | * | + | *Mit welcher mittleren Kraft schiebt Karla, wenn sie eine halbe (ganze) Sekunde lang geschoben hat? |
| − | * | + | |
| − | + | ||
| − | ===6 | + | ====6) Roller fahren==== |
| − | + | [[Datei:Tretroller.jpg|thumb|100px]] | |
| − | + | Tina steht mit ihrem Roller auf einer ebenen Straße. Zusammen haben sie eine Masse von 50kg. Dann schubst sie sich zweimal von der Straße ab. Beim ersten Mal eine Sekunde lang mit einer Kraft von 100N, beim zweiten Mal eine halbe Sekunde lang mit einer Kraft von 60N. Dazwischen rollt sie für zwei Sekunden. | |
| + | *Wieviel Impuls hat Tina nach dem ersten und nach dem zweiten Anschubsen und wie schnell ist sie jeweils? (Rechne ohne Reibung, also ohne Impulsverlust.) | ||
| − | + | Die gerade eben noch vernachlässigte Reibungskraft beträgt für Tina und ihren Roller konstant 10 Newton. | |
| − | + | *Wie lange nach dem zweimaligen Anschubsen kann Tina noch rollen, bevor sie stehen bleibt? | |
| − | + | *Wie könnte sie sich in regelmäßigen Abständen vom Boden abstoßen, um mit gleichbleibender Geschwindigkeit zu fahren? | |
| − | === | + | ====7) Das Wasserbehältermodell II==== |
| − | + | Beschreibe jeweils die Situationen oder Abläufe, indem du passende Wasserbehältermodelle mit dem richtigen Zu- und Abfluß zeichnest. | |
| − | + | ||
| − | [[Datei: | + | *Paul und Pauline fahren Skatebord |
| − | + | :Paul und Pauline stehen mit ihrem Skateboard auf der Straße. Beide stoßen sich für eine halbe Sekunde mit einer Kraft von 80 Newton vom Boden ab. Paul hat aber doppelt so viel Masse wie Pauline. | |
| − | + | ||
| − | + | *Pauline und Antonia fahren zusammen Fahrrad | |
| − | + | :Beide haben in etwa die gleiche Masse und sind auch gleichschnell. Vor der Ampel kommt Pauline innerhalb von drei Sekunden zum Stehen. Antonia dagegen kann mit ihren besseren Bremsen sogar in anderthalb Sekunden anhalten. | |
| − | + | ||
| − | + | *Pauline fährt Rad | |
| − | [ | + | :Zuerst steht sie an der Ampel. Dann tritt sie mit einer gleichbleibenden Kraft in die Pedale, bis sie schließlich mit konstanter Geschwindigkeit fährt. Nach einer Weile hört sie auf zu treten und läßt es gemütlich ausrollen. |
| − | + | ||
| − | [[ | + | ====8) Widerstände beim Radfahren==== |
| − | + | [[Datei:Fahrrad_Widerstandsdiagramm.png|thumb|250px]] | |
| + | In diesem Widerstandsdiagramm ist die Reibungskraft F über die Geschwindigkeit aufgetragen. Die Reibungskraft setzt sich aus dem geschwindigkeitsunabhängigen Rollwiderstand und der Luftreibung zusammen. | ||
| + | |||
| + | Paula fährt auf ebener Strecke mit einer konstanten Geschwindigkeit von 6 m/s. | ||
| + | *Wie groß ist jetzt die Reibungskraft und wie groß die antreibende Kraft? | ||
| + | Danach tritt Paula so in die Pedale, dass die antreibende Kraft auf 40N ansteigt. | ||
| + | *Wie schnell wird sie jetzt? | ||
| + | |||
| + | ====9) Die Weltraumwaage SLAMMD==== | ||
| + | Das "Space Linear Acceleration Mass Measurement Device", kurz SLAMMD bestimmt auf der ISS (International Space Station) die Masse von AstronautInnen durch eine lineare Beschleunigung. ([http://www.youtube.com/watch?v=qE4OoE93fX0 Demovideo]) | ||
| + | |||
| + | Bei einer Messung wurde die Person durch eine Kraft von 50 Newton in 1,2 Sekunden auf eine Geschwindigkeit von 0,8 Meter pro Sekunde beschleunigt. | ||
| + | |||
| + | *Wie groß ist deren (träge) Masse? | ||
| + | |||
| + | ====10) Der Anschnallgurt==== | ||
| + | Der Gurt verhindert bei einem Autounfall stärkere Verletzungen. | ||
| + | |||
| + | Wie groß sind wohl die Kräfte auf den Kopf der FahrerIn bei einem Aufprall mit 50 km/h auf ein festes Hindernis mit und ohne Gurt? | ||
| + | |||
| + | Mit Hilfe dieses [http://www.youtube.com/watch?v=QiEtaTROW_4&feature=related Videos vom TCS] wurde die Zeitdauer des Abremsens des Kopfes mit und ohne Gurt abgeschätzt. In den Zeitlupenaufnahmen wurden ca. 500 Bilder pro Sekunde aufgenommen, also alle 2 msec ein Bild gemacht. | ||
| + | |||
| + | :Abremsen durch Aufprall auf Frontscheibe und Lenkrad: ca. 6 msec | ||
| + | :Abremsen durch den Gurt: ca. 44 msec | ||
| + | |||
| + | Ein menschlicher Kopf hat eine Masse von ca. 3-4kg ([http://hypertextbook.com/facts/2006/DmitriyGekhman.shtml], [http://www.smf.org/docs/articles/pdf/chingtechbrief.pdf]). | ||
| − | + | *Berechne die wirkenden Kräfte beim Abbremsen und vergleiche sie mit der Gewichtskraft des Kopfes. | |
Version vom 13. Mai 2019, 05:56 Uhr
Leere Seite
Aufgaben zur Impulsmenge und zum 2. Newtonschen Gesetz
1) Impulsmengen berechnen
Berechne jeweils die Impulsmenge:
- a) Ein Vogel mit der Masse 100 g fliegt mit 36 km/h.
- b) Ein Fußgänger (m=72 kg) läuft mit 5 km/h.
- c) Ein Auto (m=1 t) fährt mit 36 km/h.
2) Bewegungsmenge im Wasserbehältermodell
Anke und ihr Papa fahren zusammen Rad. Anke wiegt 40 kg, ihr Vater 90 kg, jedes ihrer Räder 10kg. Sie fahren mit 18 km/h nebeneinander.
- a) Wieviel Impuls steckt in Anna, in ihrem Vater und wieviel in den beiden Rädern?
- Stelle dies mit dem Wasserbehältermodell dar.
- b) Wie schnell muss Anke fahren, um genausoviel Impuls wie ihr Vater zu haben? (mit Rädern)
- Stelle auch dies im Wasserbehältermodell dar.
3) Ball und Gewehrkugel
Ein Tennisball (m=57g) kann bei einer Geschwindigkeit von 5 km/h einen Holzklotz umschmeißen.
- Wie schnell muß dazu eine Luftgewehrkugel sein, wenn sie nur 0,541 g Masse hat?
4) Das Wasserbehältermodell I
- In der Tabelle ist außer der ersten Spalte einiges durcheinandergeraten. Sortiere es wieder richtig.
| Bewegung | Wasserbehälter |
|---|---|
| Impulsmenge | Grundfläche |
| Masse | Wassermenge |
| Geschwindigkeit | Abflussrate |
| Kraft | Zuflussrate |
| Reibungskraft | Wasserhöhe |
5) Jemanden anschieben
Moritz wird von Karla wird auf einem Bürodrehstuhl angeschoben. Seine (träge) Masse beträgt 70kg und die des Stuhls 10kg. Dabei wird er 2 m/sec schnell.
- Wieviel Impuls steckt in Moritz und wieviel im Stuhl?
- Mit welcher mittleren Kraft schiebt Karla, wenn sie eine halbe (ganze) Sekunde lang geschoben hat?
6) Roller fahren
Tina steht mit ihrem Roller auf einer ebenen Straße. Zusammen haben sie eine Masse von 50kg. Dann schubst sie sich zweimal von der Straße ab. Beim ersten Mal eine Sekunde lang mit einer Kraft von 100N, beim zweiten Mal eine halbe Sekunde lang mit einer Kraft von 60N. Dazwischen rollt sie für zwei Sekunden.
- Wieviel Impuls hat Tina nach dem ersten und nach dem zweiten Anschubsen und wie schnell ist sie jeweils? (Rechne ohne Reibung, also ohne Impulsverlust.)
Die gerade eben noch vernachlässigte Reibungskraft beträgt für Tina und ihren Roller konstant 10 Newton.
- Wie lange nach dem zweimaligen Anschubsen kann Tina noch rollen, bevor sie stehen bleibt?
- Wie könnte sie sich in regelmäßigen Abständen vom Boden abstoßen, um mit gleichbleibender Geschwindigkeit zu fahren?
7) Das Wasserbehältermodell II
Beschreibe jeweils die Situationen oder Abläufe, indem du passende Wasserbehältermodelle mit dem richtigen Zu- und Abfluß zeichnest.
- Paul und Pauline fahren Skatebord
- Paul und Pauline stehen mit ihrem Skateboard auf der Straße. Beide stoßen sich für eine halbe Sekunde mit einer Kraft von 80 Newton vom Boden ab. Paul hat aber doppelt so viel Masse wie Pauline.
- Pauline und Antonia fahren zusammen Fahrrad
- Beide haben in etwa die gleiche Masse und sind auch gleichschnell. Vor der Ampel kommt Pauline innerhalb von drei Sekunden zum Stehen. Antonia dagegen kann mit ihren besseren Bremsen sogar in anderthalb Sekunden anhalten.
- Pauline fährt Rad
- Zuerst steht sie an der Ampel. Dann tritt sie mit einer gleichbleibenden Kraft in die Pedale, bis sie schließlich mit konstanter Geschwindigkeit fährt. Nach einer Weile hört sie auf zu treten und läßt es gemütlich ausrollen.
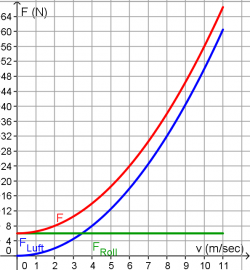
8) Widerstände beim Radfahren
In diesem Widerstandsdiagramm ist die Reibungskraft F über die Geschwindigkeit aufgetragen. Die Reibungskraft setzt sich aus dem geschwindigkeitsunabhängigen Rollwiderstand und der Luftreibung zusammen.
Paula fährt auf ebener Strecke mit einer konstanten Geschwindigkeit von 6 m/s.
- Wie groß ist jetzt die Reibungskraft und wie groß die antreibende Kraft?
Danach tritt Paula so in die Pedale, dass die antreibende Kraft auf 40N ansteigt.
- Wie schnell wird sie jetzt?
9) Die Weltraumwaage SLAMMD
Das "Space Linear Acceleration Mass Measurement Device", kurz SLAMMD bestimmt auf der ISS (International Space Station) die Masse von AstronautInnen durch eine lineare Beschleunigung. (Demovideo)
Bei einer Messung wurde die Person durch eine Kraft von 50 Newton in 1,2 Sekunden auf eine Geschwindigkeit von 0,8 Meter pro Sekunde beschleunigt.
- Wie groß ist deren (träge) Masse?
10) Der Anschnallgurt
Der Gurt verhindert bei einem Autounfall stärkere Verletzungen.
Wie groß sind wohl die Kräfte auf den Kopf der FahrerIn bei einem Aufprall mit 50 km/h auf ein festes Hindernis mit und ohne Gurt?
Mit Hilfe dieses Videos vom TCS wurde die Zeitdauer des Abremsens des Kopfes mit und ohne Gurt abgeschätzt. In den Zeitlupenaufnahmen wurden ca. 500 Bilder pro Sekunde aufgenommen, also alle 2 msec ein Bild gemacht.
- Abremsen durch Aufprall auf Frontscheibe und Lenkrad: ca. 6 msec
- Abremsen durch den Gurt: ca. 44 msec
Ein menschlicher Kopf hat eine Masse von ca. 3-4kg ([1], [2]).
- Berechne die wirkenden Kräfte beim Abbremsen und vergleiche sie mit der Gewichtskraft des Kopfes.