Aufgaben zur Impulsveränderung durch Kraft (Lösungen): Unterschied zwischen den Versionen
(→Das Wasserbehältermodell I) |
(→Roller fahren) |
||
| Zeile 94: | Zeile 94: | ||
:Die Geschwindigkeiten erhält man durch Division durch die Masse: | :Die Geschwindigkeiten erhält man durch Division durch die Masse: | ||
::<math>p=m\, v \quad \Rightarrow \quad v = \frac{p}{m}</math> | ::<math>p=m\, v \quad \Rightarrow \quad v = \frac{p}{m}</math> | ||
| − | ::<math>v(\rm 1\, s)=\frac{100\, Hy}{50 \, kg}= 2\,\frac{m}{s}\approx 7\, \frac{km}{h} </math> <math> | + | ::<math>v(\rm 1\, s)=\frac{100\, Hy}{50 \, kg}= 2\,\frac{m}{s}\approx 7\, \frac{km}{h} </math> <math>\text{}\qquad v(\rm 3{,}5\, s)=\frac{130\, Hy}{50 \, kg}= 2{,}6\,\frac{m}{s}\approx 9{,}5\, \frac{km}{h}.</math> |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
Die gerade eben noch vernachlässigte Reibungskraft beträgt für Tina und ihren Roller konstant 10 Newton. | Die gerade eben noch vernachlässigte Reibungskraft beträgt für Tina und ihren Roller konstant 10 Newton. | ||
| Zeile 124: | Zeile 107: | ||
:Tina kann also noch 9,5 Sekunden lang rollen ohne sich abzustoßen. | :Tina kann also noch 9,5 Sekunden lang rollen ohne sich abzustoßen. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
*Wie könnte sie sich in regelmäßigen Abständen vom Boden abstoßen, um mit gleichbleibender Geschwindigkeit zu fahren? | *Wie könnte sie sich in regelmäßigen Abständen vom Boden abstoßen, um mit gleichbleibender Geschwindigkeit zu fahren? | ||
Version vom 13. Mai 2019, 11:30 Uhr
(Physik Sekundarstufe I > Kraft und Bewegung ("Dynamik"))
Inhaltsverzeichnis
Grundlagen
2. Newtonsches Gesetz
- Wie lautet das 2. Newtonsche Gesetz?
- Je fester an einem Gegenstand gedrückt (gezogen) wird und je länger das geschieht, desto mehr ändert sich seine Impulsmenge.
- [math]\Delta p = F\, \Delta t [/math]
- Die Kraft ist die Änderung des Impulses pro Zeit.
- [math]F=\frac{\Delta p}{\Delta t}[/math]
- Erläutere es auch an einem selbstgewählten Beispiel.
- Ich stehe auf einem Skateboard und drücke mich eine halbe Sekunde von der Straße mit einer Kraft von 100 Newton ab. Dabei vergrößert sich mein Impuls um 50 Huygens:
- [math]\Delta p = F\, \Delta t = 100\,\rm N \cdot 0{,}5\,\rm s = 50\,\rm Hy[/math]
- Dann lasse ich den Fuß am Boden schleifen und bremse dadurch. Mein Impuls nimmt innerhalb von 5 Sekunden um 20 Huygens ab. Die Bremskraft betrug daher gerade 4 Newton.
- [math]F=\frac{\Delta p}{\Delta t}= \mathrm{\frac{20\,Hy}{5\,s} = 4\,N}[/math]
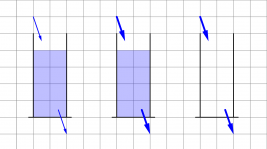
Das Wasserbehältermodell I
|
|
Einheitenpuzzle und Sprachwirrwarr
In der jeweils linken Spalte stehen die richtigen Aussagen!
| Der Impuls gibt die Bewegungsmenge an. | Der Impuls bestimmt die Kraft der Bewegung. |
| Der Impuls eines Körpers verändert sich nicht ohne eine Kraft. | Ein Körper verändert sich nicht ohne Impuls. |
| Beim Losfahren bekommt man Impuls. | Beim Losfahren bekommt man einen Impuls. |
| Das Auto fährt durch die große Kraft ruckartig los. | Das Auto fährt durch den großen Impuls ruckartig los. |
| Wenn das Auto anfährt, drückt es Peter nach vorn und gibt ihm Impuls. | Wenn das Auto fährt, erfährt Peters Körper seinen Impuls. |
| Eine Kraft führt Impuls zu und verändert die Impulsmenge. | Ein Impuls ist eine zugeführte Kraft, die Veränderung erbringt. |
| Peter kann mit einer großen Kraft drücken. | Peter hat viel Kraft. |
Jemanden anschieben
Eine Person wird auf einem Bürodrehstuhl angeschoben. Ihre (träge) Masse beträgt 70kg und die des Stuhls 10kg. Dabei wird sie 2m/sec schnell.
- Die Impulsmengen betragen:
- Person: [math]p= m\, v = 70\, \rm kg \cdot 2\, \rm m/s = 140\, \rm Hy[/math]
- Stuhl: [math]p= m\, v = 10\, \rm kg \cdot 2\, \rm m/s = 20\, \rm Hy[/math]
- Zusammen also [math]160 \,\rm Hy[/math]
- Weil hier der Stuhl vor der Beschleunigung in Ruhe war, also noch keinen Impuls hatte, ist die Impulsänderung genau die Impulsmenge nach dem Anschubsen. Nach dem Veränderungsgesetz ist die Kraft Impulsänderung pro Zeit:
- [math]F=\frac{\triangle p }{ \triangle t}= \frac{160 \, \rm{Hy}}{1\, \rm{s}}= 160\frac{\rm Hy}{\rm s}=160\,\rm N[/math]
- Bei einer Sekunde hat man also mit 160N geschoben, bei der halben Zeitspanne muss die mittlere Kraft doppelt so groß gewesen sein.
Losfahren
Eine RadlerIn beschleunigt aus dem Stand 10 Sekunden lang mit einer mittleren Kraft von 30 Newton. Zusammen mit dem Rad hat sie eine (träge) Masse von 60kg.
- Weil hier das Rad vor der Beschleunigung in Ruhe war, ist die Impulsänderung genau die Impulsmenge nach den ersten zehn Sekunden. Nach dem Veränderungsgesetz ändert sich der Impuls um:
- [math]\triangle \, p = F\, \triangle \, t = \mathrm{30\, N \cdot 10\, s = 300\, Hy}[/math]
- Aus der Definition des Impulses folgt:
- [math]p= m\, v = 300 \, \mathrm{Hy = 60\, kg} \cdot v [/math]
- [math] \Rightarrow \quad v =\mathrm{ 5\, \frac{m}{s} = 18\, \frac{km}{h}}[/math]
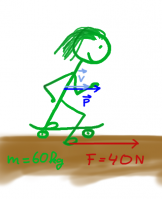
Roller fahren
Tina steht mit ihrem Roller auf einer ebenen Straße. Zusammen haben sie eine Masse von 50kg. Dann schubst sie sich zweimal von der Straße ab. Beim ersten Mal eine Sekunde lang mit einer Kraft von 100N, beim zweiten Mal eine halbe Sekunde lang mit einer Kraft von 60N. Dazwischen rollt sie für zwei Sekunden.
- Wieviel Impuls hat Tina nach dem ersten und nach dem zweiten Anschubsen und wie schnell ist sie jeweils? (Rechne ohne Reibung, also ohne Impulsverlust.)
- Die Impulsänderungen betragen:
- [math]\triangle p = F \, \triangle t = 100 \, \rm N \cdot 1\, s = 100 \, Hy[/math]
- [math]\triangle p = F \, \triangle t = 60\, \rm N \cdot 0{,}5 \, s = 30 \, Hy[/math]
- Tina hat nach dem ersten Anschubsen eine Impulsmenge von 100Hy, nach dem zweiten Anschubsen von 130Hy:
- [math]p(\rm 1\, s)=100\, Hy [/math] [math].\qquad p(\rm 3{,}5\, s)=130\, Hy .[/math]
- Die Geschwindigkeiten erhält man durch Division durch die Masse:
- [math]p=m\, v \quad \Rightarrow \quad v = \frac{p}{m}[/math]
- [math]v(\rm 1\, s)=\frac{100\, Hy}{50 \, kg}= 2\,\frac{m}{s}\approx 7\, \frac{km}{h} [/math] [math]\text{}\qquad v(\rm 3{,}5\, s)=\frac{130\, Hy}{50 \, kg}= 2{,}6\,\frac{m}{s}\approx 9{,}5\, \frac{km}{h}.[/math]
Die gerade eben noch vernachlässigte Reibungskraft beträgt für Tina und ihren Roller konstant 10 Newton.
- Wie lange nach dem zweimaligen Anschubsen kann Tina noch rollen, bevor sie stehen bleibt?
- Berücksichtigt man die Reibungskraft von 10N, so gehen in jeder Sekunde 10Hy Impuls verloren. Während der 3,5s dauernden Anschubsphase sind das:
- [math]\Delta p = 10\,\rm N \cdot 3{,}5\,\rm s = 35\,\rm Hy[/math]
Tina hat also nach dem Anschubsen nur 95 Huygens Impuls!
- In jeder Sekunde verliert sie davon 10 Huygens. Damit kann man die Ausrollzeit bestimmen:
- [math]\Delta p = F\, \Delta t \quad \Rightarrow \quad \Delta t = \frac{\Delta p}{F} = \mathrm{\frac{95\,Hy}{10\,N}=9{,}5\,s}[/math]
- Tina kann also noch 9,5 Sekunden lang rollen ohne sich abzustoßen.
- Wie könnte sie sich in regelmäßigen Abständen vom Boden abstoßen, um mit gleichbleibender Geschwindigkeit zu fahren?
- Tina muss im Durchschnitt 10 Huygens pro Sekunde Impuls erhalten, denn soviel geht durch die Reibung verloren.
- Sie könnte sich eine Sekunde lang mit 20 Newton abstoßen, dann eine Sekunde lang rollen und so weiter.
- Oder sie stößt sich eine Sekunde lang mit 30 Newton ab, dann kann sie zwei Sekunden lang rollen und so weiter.
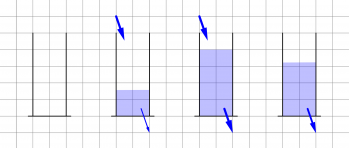
Das Wasserbehältermodell II
Beschreibe jeweils die Situationen oder Abläufe, indem du passende Wasserbehältermodelle findest.
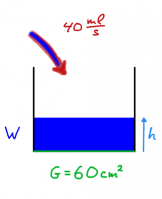
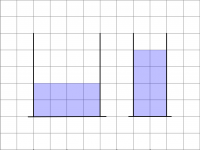
- Paul und Pauline fahren Skatebord
- Paul und Pauline stehen mit ihrem Skateboard auf der Straße. Beide stoßen sich für eine halbe Sekunde mit einer Kraft von 80 Newton vom Boden ab. Paul hat aber doppelt so viel Masse wie Pauline.
- Beide stoßen sich auf die gleiche Weise vom Boden ab und erhalten deswegen beide die gleiche Impulsmenge von 40 Huygens. Weil Paul die doppelte Masse hat, ist er nur halb so schnell wie Paula.
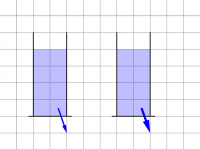
- Pauline und Antonia fahren zusammen Fahrrad
- Beide haben in etwa die gleiche Masse und sind auch gleichschnell. Vor der Ampel kommt Pauline innerhalb von drei Sekunden zum Stehen. Antonia dagegen kann mit ihren besseren Bremsen sogar in anderthalb Sekunden anhalten.
- Beide haben den gleichen Impuls, den sie aber unterschiedlich schnell verlieren. Bei Pauline wirkt im gleichen Zeitraum eine halb so große Kraft wie bei Antonia.
- Paul zieht Pauline auf dem Schlitten
- Zunächst geht es mit einer gleichbleibenden Geschwindigkeit über den Schnee. Dann aber kommt eine Straße und Paul zieht so, dass sie trotzdem die Geschwindigkeit beibehalten. Schließlich aber bleibt der Schlitten stecken und trotz Ziehens ist der Schlitten nicht mehr zu bewegen.
- Schnee
Bei konstanter Geschwindigkeit ist auch die Impulsmenge konstant. Durch das Ziehen am Schlitten führt Paul dem Schlitten und Pauline Impuls zu. Aber gleichzeitig geht durch die Reibung die gleiche Impulsmenge wieder verloren. - Straße
Auch hier ist die Impulsmenge konstant. Aber wegen der größeren Reibung muss Paul fester ziehen. - Straße, steckengeblieben
Weil der Schlitten steht, ist kein Impuls im Schlitten oder in Paula. Wegen der starken Haftung am Boden geht sämtlicher Impuls, den Paul durch sein Ziehen hineinsteckt, sofort wieder verloren.
- Pauline fährt Rad
- Zuerst steht sie an der Ampel. Dann tritt sie mit einer gleichbleibenden Kraft in die Pedale, bis sie schließlich mit konstanter Geschwindigkeit fährt. Nach einer Weile hört sie auf zu treten und läßt es gemütlich ausrollen.
- Stehen
Beim Stehen hat Pauline noch keinen Impuls. - Losfahren
Wenn sie losfährt wird durch ihr gleichmäßiges Treten der Impuls gleichmäßig zunehmen. Wenn sie langsam fährt, ist ihre Reibung noch gering und es geht wenig Impuls verloren. - konstante Geschwindigkeit
Je schneller sie fährt, desto größer wird auch ihre Reibung, vor allem wegen des Luftwiderstandes. Durch ihr Treten ist ihre Impulsmenge schließlich so groß geworden, bis genausoviel Impuls reingeht wie rausgeht. - Ausrollen
Es kommt kein Impuls mehr hinzu. Durch die Reibungskraft nimmt deswegen der Impuls wieder ab.
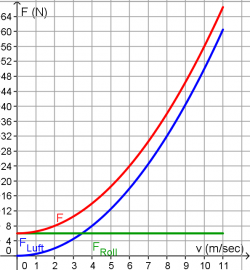
Widerstände beim Radfahren
In diesem Widerstandsdiagramm ist die Reibungskraft F über die Geschwindigkeit aufgetragen. Die Reibungskraft setzt sich aus dem geschwindigkeitsunabhängigen Rollwiderstand und der Luftreibung zusammen.
Paula fährt auf ebener Strecke mit einer konstanten Geschwindigkeit von 6 m/s.
- Wie groß ist jetzt die Reibungskraft und wie groß die antreibende Kraft?
- Wenn Paula mit einer konstanten Geschwindigkeit fährt, dann verändert sich auch der Impuls nicht. Deshalb muss durch Paulas antreibende Kraft genausoviel Impuls reingehen, wie durch die Reibungskraft wieder rausgeht.
- Beide Krafte sind also gleich groß, Paula ist im "Kräftegleichgewicht".
- Am Diagramm kann man ablesen, dass die gesamte Reibungskraft bei 6 m/s gerade 24N beträgt. Paula treibt sich also mit einer Kraft von 24N an.
Danach tritt Paula so in die Pedale, dass die antreibende Kraft auf 40N ansteigt.
- Wie schnell wird sie jetzt?
- Auch jetzt wird sie so schnell, dass wieder Kräftegleichgewicht eintritt. Das ist bei einer Geschwindigkeit von ca. 8,2 m/s (30 km/h) der Fall.
Praktische Anwendungen
Die Weltraumwaage SLAMMD
Das "Space Linear Acceleration Mass Measurement Device", kurz SLAMMD bestimmt auf der ISS (International Space Station) die Masse von AstronautInnen durch eine lineare Beschleunigung. (Demovideo)
Bei einer Messung wurde die Person durch eine Kraft von 50 Newton in 1,2 Sekunden auf eine Geschwindigkeit von 0,8 Meter pro Sekunde beschleunigt.
- Man kann den Impuls der Astronautin auf zwei Arten bestimmen. Einmal über das Veränderungsgesetz als Ergebnis der Kraftwirkung und einmal über die Definition des Impulses als Masse mal Geschwindigkeit. Auch hier ist die Impulsänderung genau die Impulsmenge nach der Beschleunigung, weil die Astronautin zu Beginn noch keinen Impuls hat:
- [math] m\, v = \triangle \, p = F\, \triangle \, t[/math]
- Nach der Masse aufgelöst:
- [math]m= \frac{F\, \triangle \, t}{v} = \rm \frac{50\, \rm N \cdot \, 1{,}2\, s}{0{,}8\, m/s} = \frac{60\, \rm Hy}{0{,}8\, m/s} = 75\,kg[/math]
- Die Masse beträgt 75kg.
Der Anschnallgurt
Der Gurt verhindert bei einem Autounfall stärkere Verletzungen.
Wie groß sind wohl die Kräfte auf den Kopf der FahrerIn bei einem Aufprall mit 50 km/h auf ein festes Hindernis mit und ohne Gurt?
Mit Hilfe dieses Videos vom TCS wurde die Zeitdauer des Abremsens des Kopfes mit und ohne Gurt abgeschätzt. In den Zeitlupenaufnahmen wurden ca. 500 Bilder pro Sekunde aufgenommen, also alle 2 msec ein Bild gemacht.
- Abremsen durch Aufprall auf Frontscheibe und Lenkrad: ca. 6 msec
- Abremsen durch den Gurt: ca. 44 msec
Ein menschlicher Kopf hat eine Masse von ca. 3-4kg ([1], [2]).
- Berechne die wirkenden Kräfte beim Abbremsen und vergleiche sie mit der Gewichtskraft des Kopfes.
Weihnachtsbaumtransport
In diesem Video des ADAC wurde der Transport eines Weihnachtsbaumes auf dem Autodach untersucht.
Zitat: "Eine mannshohe Tanne bringt um die 30kg auf die Waage. Bei einem Aufprall mit 50km/h zerren in diesem Fall 750kg am Dachträger."
- Mit den 30kg ist sicherlich die Masse der Tanne gemeint, die vor der Fahrt gewogen wurde. Während des Abbremsens muss der Dachträger mit einer großen Kraft an der Tanne drücken, um sie anzuhalten. Nun kann man zum Vergleich diese Bremskraft in eine Gewichtskraft einer fiktiven Tanne umrechnen. Hätte die Tanne eine Masse von 750kg, so würde deren Gewichtskraft der Bremskraft entsprechen.
- Die Tanne bewegt sich mit einer Geschwindigkeit von:
- [math]v= 50\; \colon 3{,}6\rm\frac{m}{s} = 13{,}9\rm\frac{m}{s}[/math]
- Der Impuls der Tanne beträgt daher:
- [math]p=m\,v = 30\,\rm kg \cdot 13{,}9\rm\frac{m}{s} = 416\,\rm Hy[/math]
- Die Bremskraft soll einer Gewichtskraft von 750kg entsprechen:
- [math]F=750\,\rm kg \cdot 10\rm\frac{N}{kg}=7500\,\rm N[/math]
- Die Kraft gibt an, wie schnell sich der Impuls ändert. Das 2. Newtonsche Gesetz löst man dann nach der Zeit auf:
- [math]\Delta p = F\, \Delta t \quad \Rightarrow \quad \Delta t= \frac{\Delta p}{F} = \frac{416\,\rm Hy}{7500\,\rm N} = 0{,}055\,\rm s = 55\,ms[/math]
- Der Baum wird also in ca. 6 Hundertstel Sekunden abgebremst.