Gruppenpuzzle Kinematik-Dynamik: Unterschied zwischen den Versionen
(→Auswertung eines 10-Meter Laufs) |
(→Die Weltraumwaage SLAMMD) |
||
| (11 dazwischenliegende Versionen des gleichen Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | == | + | ==Bremswege== |
| − | + | Aus Sicherheitsgründen wird oft die Einrichtung einer Tempo 30 Zone gefordert, vor allem in Wohngebieten, bei denen auch viele Kinder spielen. Aber bringt denn der Unterschied zwischen 50km/h und 30km/h so viel? | |
| − | + | ||
| − | + | Dazu kann man die verschiedenen Bremswege vergleichen. Auf der Seite www.unfallaufnahme.info findet man folgende Werte für die Bremsverzögerungen bei Vollbremsungen. Die Werte geben an, wie sich die Geschwindigkeit in einer Sekunde verringert. | |
| − | + | {| | |
| − | + | |Trockene Asphaltfahrbahn / Schwarzdecke: ||7,5 - 8,0 m/s<sup>2</sup> | |
| − | + | |- | |
| + | |Schneebedeckte Fahrbahn: || 2,0 - 3,0 m/s<sup>2</sup> | ||
| + | |- | ||
| + | |Motorrad (nur Hinterrad wird abgebremst): || 4,0 m/s<sup>2</sup> | ||
| + | |- | ||
| + | |Motorrad (nur Vorderrad wird abgebremst): || 6,5 m/s<sup>2</sup> | ||
| + | |- | ||
| + | |Motorrad (optimaler Bremseinsatz): || 10 m/s<sup>2</sup> | ||
| + | |} | ||
| + | '''a)''' Rechne die Geschwindigkeit in m/s um und zeichne für ein Auto die beiden Geschwindigkeitsdiagramme einer Vollbremsung auf trockener Fahrbahn von 50km/h und 30km/h zusammen in ein Koordinatensystem. | ||
| + | |||
| + | Bestimme aus den Diagrammen die verschiedenen Bremswege. | ||
| + | |||
| + | '''b)''' Begründe folgende allgemeine Formeln für die Bremszeit und den Bremsweg: | ||
| + | :<math>t_{brems} = \frac{v_0}{a} </math> | ||
| + | :<math>s_{brems} = \frac{1}{2} \frac{v_0^2}{a}</math> | ||
| + | |||
| + | Wie verändert sich der Bremsweg und die Bremszeit, wenn sich die Ausgangsgeschwindigkeit verdoppelt oder halbiert? | ||
| + | |||
| + | '''c)''' Stelle mit Hilfe der Formel für den Bremsweg eine Tabelle auf mit den Bremswegen bei 50km/h und 30km/h für alle verschiedenen Verzögerungwerte aus der oberen Übersicht. | ||
==Mit dem Fahrrad bergab rollen== | ==Mit dem Fahrrad bergab rollen== | ||
| Zeile 15: | Zeile 33: | ||
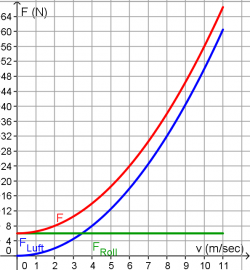
Dazu bestimmt sie das Gefälle der Straße zu 10%, ihre Masse zu 50 kg, die Masse des Rads zu 10 kg und im Internet findet sie noch ein Diagramm, das ihr angibt wie die Widerstandskraft von der Geschwindigkeit abhängt. | Dazu bestimmt sie das Gefälle der Straße zu 10%, ihre Masse zu 50 kg, die Masse des Rads zu 10 kg und im Internet findet sie noch ein Diagramm, das ihr angibt wie die Widerstandskraft von der Geschwindigkeit abhängt. | ||
| − | + | '''a)''' Warum kann man für die Betrachtung der ersten drei Sekunden der Bewegung den Luftwiderstand noch vernachlässigen und Annas Bewegung als gleichmäßig beschleunigt ansehen? | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | :<math> \ | + | '''b)''' Um die beschleunigende Kraft zu berechnen, findet Anna folgende Formel: |
| − | + | :<math>F_{Hang} \approx m\,g\cdot \text{Gefälle}</math> | |
| − | + | und dann zieht sie von diesem Ergebnis noch 6 Newton ab. | |
| − | + | Berechne damit die beschleunigende Kraft und daraus die Beschleunigung. | |
| − | + | '''c)''' Wie schnell wird Anna innerhalb der ersten drei Sekunden? Und wie weit rollt sie dabei? | |
| − | + | ||
| − | + | ||
| + | Rechne dazu mit den Bewegungsgesetzen der gleichmäßig beschleunigten Bewegung und zeichne ein Geschwindigkeitsdiagramm (x: Zeit ; y: Geschwindigkeit) der ersten drei Sekunden. | ||
| + | |||
| + | '''d)''' Nach ca. einer Minute Rollen hat Anna schon ihre maximale Geschwindigkeit erreicht. | ||
| + | |||
| + | Bestimme mit Hilfe des Widerstands-Diagramms Annas maximale Geschwindigkeit. | ||
| + | |||
| + | Zeichne das Geschwindigkeitsdiagramm der ersten Minute so gut es möglich ist. | ||
==Die Weltraumwaage SLAMMD== | ==Die Weltraumwaage SLAMMD== | ||
| − | Das "Space Linear Acceleration Mass Measurement Device", kurz SLAMMD bestimmt auf der ISS (International Space Station) die Masse von AstronautInnen durch eine lineare Beschleunigung. ([ | + | Das "Space Linear Acceleration Mass Measurement Device", kurz SLAMMD bestimmt auf der ISS (International Space Station) die Masse von AstronautInnen durch eine lineare Beschleunigung. ([https://vimeo.com/465955155 Demovideo]) |
| + | |||
| + | Bei einer Messung wurde die Person durch eine Kraft von 50 Newton längs einer Strecke von 60cm beschleunigt, wofür 1,2 Sekunden benötigt wurden. | ||
| + | |||
| + | '''a)''' Welche Art von Bewegung führt die AstronautIn aus? | ||
| − | + | '''b)''' Berechne die Beschleunigung mit Hilfe des Orts-Gesetzes. | |
| + | |||
| + | '''c)''' Welche maximale Geschwindigkeit hat sie erreicht? | ||
| − | + | '''d)''' Wie groß ist ihre (träge) Masse? (Dazu gibt es zwei Lösungswege: Entweder über den Impuls <math>p=m\,v</math> mit <math>F=\frac{\Delta p}{\Delta t}</math> oder über die Beschleunigung <math>a=\frac{F}{m}</math>) | |
==Auswertung eines 100-Meter Laufs== | ==Auswertung eines 100-Meter Laufs== | ||
| Zeile 96: | Zeile 120: | ||
|} | |} | ||
| − | '''a)''' Wie groß ist ihre | + | '''a)''' Wie groß ist ihre Durchschnittsgeschwindigkeit in den gesamten 100 Metern? |
'''b)''' In welchen Wegintervall erreicht sie die höchste und in welchem die niedrigste Durchschnittsgeschwindigkeit? | '''b)''' In welchen Wegintervall erreicht sie die höchste und in welchem die niedrigste Durchschnittsgeschwindigkeit? | ||
'''c)''' Man kann die erste Phase des Laufes vereinfacht als gleichmäßig beschleunigte Bewegung ansehen. Wie groß ist dann ihre Beschleunigung auf den ersten 5 Metern? Mit welcher Kraft hat sie beschleunigt? | '''c)''' Man kann die erste Phase des Laufes vereinfacht als gleichmäßig beschleunigte Bewegung ansehen. Wie groß ist dann ihre Beschleunigung auf den ersten 5 Metern? Mit welcher Kraft hat sie beschleunigt? | ||
Aktuelle Version vom 14. September 2021, 15:33 Uhr
Inhaltsverzeichnis
Bremswege
Aus Sicherheitsgründen wird oft die Einrichtung einer Tempo 30 Zone gefordert, vor allem in Wohngebieten, bei denen auch viele Kinder spielen. Aber bringt denn der Unterschied zwischen 50km/h und 30km/h so viel?
Dazu kann man die verschiedenen Bremswege vergleichen. Auf der Seite www.unfallaufnahme.info findet man folgende Werte für die Bremsverzögerungen bei Vollbremsungen. Die Werte geben an, wie sich die Geschwindigkeit in einer Sekunde verringert.
| Trockene Asphaltfahrbahn / Schwarzdecke: | 7,5 - 8,0 m/s2 |
| Schneebedeckte Fahrbahn: | 2,0 - 3,0 m/s2 |
| Motorrad (nur Hinterrad wird abgebremst): | 4,0 m/s2 |
| Motorrad (nur Vorderrad wird abgebremst): | 6,5 m/s2 |
| Motorrad (optimaler Bremseinsatz): | 10 m/s2 |
a) Rechne die Geschwindigkeit in m/s um und zeichne für ein Auto die beiden Geschwindigkeitsdiagramme einer Vollbremsung auf trockener Fahrbahn von 50km/h und 30km/h zusammen in ein Koordinatensystem.
Bestimme aus den Diagrammen die verschiedenen Bremswege.
b) Begründe folgende allgemeine Formeln für die Bremszeit und den Bremsweg:
- [math]t_{brems} = \frac{v_0}{a} [/math]
- [math]s_{brems} = \frac{1}{2} \frac{v_0^2}{a}[/math]
Wie verändert sich der Bremsweg und die Bremszeit, wenn sich die Ausgangsgeschwindigkeit verdoppelt oder halbiert?
c) Stelle mit Hilfe der Formel für den Bremsweg eine Tabelle auf mit den Bremswegen bei 50km/h und 30km/h für alle verschiedenen Verzögerungwerte aus der oberen Übersicht.
Mit dem Fahrrad bergab rollen
Anna rollt aus dem Stand den Schauinsland herunter. Sie möchte gerne wissen, wie schnell sie nach einer gewissen Zeit wird und welche maximale Geschwindigkeit sie erreichen kann.
Dazu bestimmt sie das Gefälle der Straße zu 10%, ihre Masse zu 50 kg, die Masse des Rads zu 10 kg und im Internet findet sie noch ein Diagramm, das ihr angibt wie die Widerstandskraft von der Geschwindigkeit abhängt.
a) Warum kann man für die Betrachtung der ersten drei Sekunden der Bewegung den Luftwiderstand noch vernachlässigen und Annas Bewegung als gleichmäßig beschleunigt ansehen?
b) Um die beschleunigende Kraft zu berechnen, findet Anna folgende Formel:
- [math]F_{Hang} \approx m\,g\cdot \text{Gefälle}[/math]
und dann zieht sie von diesem Ergebnis noch 6 Newton ab.
Berechne damit die beschleunigende Kraft und daraus die Beschleunigung.
c) Wie schnell wird Anna innerhalb der ersten drei Sekunden? Und wie weit rollt sie dabei?
Rechne dazu mit den Bewegungsgesetzen der gleichmäßig beschleunigten Bewegung und zeichne ein Geschwindigkeitsdiagramm (x: Zeit ; y: Geschwindigkeit) der ersten drei Sekunden.
d) Nach ca. einer Minute Rollen hat Anna schon ihre maximale Geschwindigkeit erreicht.
Bestimme mit Hilfe des Widerstands-Diagramms Annas maximale Geschwindigkeit.
Zeichne das Geschwindigkeitsdiagramm der ersten Minute so gut es möglich ist.
Die Weltraumwaage SLAMMD
Das "Space Linear Acceleration Mass Measurement Device", kurz SLAMMD bestimmt auf der ISS (International Space Station) die Masse von AstronautInnen durch eine lineare Beschleunigung. (Demovideo)
Bei einer Messung wurde die Person durch eine Kraft von 50 Newton längs einer Strecke von 60cm beschleunigt, wofür 1,2 Sekunden benötigt wurden.
a) Welche Art von Bewegung führt die AstronautIn aus?
b) Berechne die Beschleunigung mit Hilfe des Orts-Gesetzes.
c) Welche maximale Geschwindigkeit hat sie erreicht?
d) Wie groß ist ihre (träge) Masse? (Dazu gibt es zwei Lösungswege: Entweder über den Impuls [math]p=m\,v[/math] mit [math]F=\frac{\Delta p}{\Delta t}[/math] oder über die Beschleunigung [math]a=\frac{F}{m}[/math])
Auswertung eines 100-Meter Laufs
Bei einem 100m-Lauf wurden für eine Läuferin (m=60kg) die folgenden Zeiten für verschiedene Ort gemessen (Achtung, für s=40m und s=60m gibt es keine Messwerte!):
|
t (in s) |
0 |
1,54 |
2,88 |
3,91 |
5,25 |
6,94 |
8,77 |
9,75 |
10,62 |
11,35 |
|
s (in m) |
0 |
5 |
10 |
20 |
30 |
50 |
70 |
80 |
90 |
100 |
a) Wie groß ist ihre Durchschnittsgeschwindigkeit in den gesamten 100 Metern?
b) In welchen Wegintervall erreicht sie die höchste und in welchem die niedrigste Durchschnittsgeschwindigkeit?
c) Man kann die erste Phase des Laufes vereinfacht als gleichmäßig beschleunigte Bewegung ansehen. Wie groß ist dann ihre Beschleunigung auf den ersten 5 Metern? Mit welcher Kraft hat sie beschleunigt?