Aufgaben zu Schwingungen: Unterschied zwischen den Versionen
(→Schaukeltier) |
(→Schwingmännchen II) |
||
| (70 dazwischenliegende Versionen des gleichen Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | ([[Inhalt_Kursstufe|'''Kursstufe''']] > [[Inhalt_Kursstufe#Mechanische Schwingungen|''' Mechanische Schwingungen''']]) | |
| + | |||
| + | |||
====Energieformen==== | ====Energieformen==== | ||
| − | Nennen Sie zwei verschiedene | + | Nennen Sie zwei verschiedene Beispiele für eine Schwingung und beschreiben Sie kurz wann dabei welche Energieformen auftreten. |
| + | [[Datei:Schaukeltier_mit_Kind.jpg|thumb]] | ||
====Schaukeltier==== | ====Schaukeltier==== | ||
| − | |||
| − | |||
Ein Kind "reitet" auf einem Feder-Schaukeltier. Erklären Sie anhand dieses Beispiels die Begriffe: | Ein Kind "reitet" auf einem Feder-Schaukeltier. Erklären Sie anhand dieses Beispiels die Begriffe: | ||
*Ruhelage | *Ruhelage | ||
| Zeile 15: | Zeile 16: | ||
Nennen Sie noch ein weiteres Beispiel für eine mechanische Schwingung und machen Sie sich wiederum diese Begriffe klar. | Nennen Sie noch ein weiteres Beispiel für eine mechanische Schwingung und machen Sie sich wiederum diese Begriffe klar. | ||
| − | ==== | + | ====Zeigermodell==== |
| − | + | Wie kann man eine harmonische Schwingung mit einem Zeiger beschreiben? | |
| − | + | ||
| − | + | ||
| − | + | Beschreiben Sie dazu den im Unterricht durchgeführten Versuch. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | [[Datei:Wecker.jpg|thumb|100px]] | |
| + | ====Uhrzeiger==== | ||
| + | Eine Uhr hat einen Stunden-, einen Minuten- und einen Sekundenzeiger. | ||
| + | *Begründen Sie warum der Sekundenzeiger eine Winkelgeschwindigkeit von <math>\omega = \frac{2\, \pi}{60\, \rm s}</math> hat. | ||
| + | *Welche Frequenz und welche Periodendauer hat der Sekundenzeiger? | ||
| + | *Mit welcher Geschwindigkeit <math>v</math> bewegt sich die Spitze des Sekundenzeigers, wenn er 10cm lang ist? | ||
| + | *Suchen Sie eine Armbanduhr oder eine Wanduhr und bestimmen Sie für alle drei Zeiger die Größen: <math>\omega</math>, <math>f</math>, <math>T</math> und <math>v</math>. | ||
| + | <br style="clear: both" /> | ||
====Schwingmännchen==== | ====Schwingmännchen==== | ||
| − | + | Ein Schwingmännchen schwingt mit einer Periodendauer von <math>\rm T = 0{,}5\, s</math> und einer Amplitude von <math>\hat y = \rm 3\, cm</math>. | |
| − | + | ||
| − | = | + | |
| − | + | ||
| − | = | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | Die Zeit <math>t</math> wird ab dem Durchgang von unten nach oben durch die Ruhelage gemessen. | |
| − | + | ||
| − | + | *Zeichnen Sie für folgende Zeitpunkte den Zeiger in ein Koordinatensystem: <math>t_1 = 0{,}25\, s</math>, <math>t_2 = 0{,}125\, s</math>, <math>t_3 = 0{,}4375\, s</math> | |
| − | + | ||
| − | + | *Bestimmen Sie zeichnerisch jeweils die Auslenkungen <math>y(t_i)</math>. | |
| − | + | ||
| − | + | ||
| − | + | [[Datei:Stimmgabel.jpg|thumb]] | |
| − | + | [[Datei:Verrußte_Glasplatte_Stimmgabel.jpg|thumb]] | |
| − | ==== | + | ====Stimmgabel==== |
| − | + | Die Zinken einer Stimmgabel schwingen mit einer Frequenz von 440 Hz<ref>Das ist der Kammerton a. (Siehe auch [http://de.wikipedia.org/wiki/Kammerton Wikipedia: Kammerton])</ref> und durch eine Messung an einer verußten Glasplatte bestimmt man die größte Amplitude zu <math>\hat y = 2 \, \rm mm</math>. | |
| + | *Welche Periodendauer und welche Winkelgeschwindigkeit hat die Schwingung? | ||
| + | *Stellen Sie für einen Zinken der Stimmgabel die Bewegungsgleichungen auf: | ||
| + | :<math>y(t)</math>, <math>v(t)</math>, <math>a(t)</math>, | ||
| + | *Bestimmen Sie daraus die maximale Geschwindigkeit und die maximale Beschleunigug eines Zinkens der Stimmgabel. | ||
| + | <br style="clear: both" /> | ||
| − | ==== | + | ====Horizontales Federpendel==== |
| − | + | {| | |
| − | + | |valign="top"| | |
| − | + | Ein Wagen schwingt horizontal an einer Feder. Die folgenden Graphen beschreiben den Verlauf seiner Bewegung im Koordinatensystem: | |
| − | + | |valign="top"| | |
| − | + | ||
| − | ==== | + | {{#widget:Iframe |
| − | + | |url=https://tube.geogebra.org/material/iframe/id/332117/width/300/height/170/border/888888/rc/false/ai/false/sdz/false/smb/false/stb/false/stbh/true/ld/false/sri/true/at/preferhtml5 | |
| + | |width=200 | ||
| + | |height=114 | ||
| + | |border=0 | ||
| + | }} | ||
| − | + | |} | |
| − | + | ||
| − | + | ||
| − | + | [[Datei:Aufgabe_Schwingung_y-t-Diagramm.png|500px]] | |
| − | + | [[Datei:Aufgabe_Schwingung_v-t-Diagramm.png|500px]] | |
| − | + | [[Datei:Aufgabe_Schwingung_a-t-Diagramm.png|500px]] | |
| − | + | *Woran kann man erkennen, dass die Schwingung nicht gedämpft ist, also keine Energie verliert? | |
| − | + | ||
| − | + | *Wie wurde dem Wagen zu Beginn Energie zugeführt? Wurde er ausgelenkt und losgelassen? (und wenn ja, in welche Richtung?) Wurde er angeschubst? (und wenn ja, in welche Richtung?) | |
| − | + | Der Graph der Geschwindigkeit ist gegenüber dem der Auslenkung um eine Viertel Periode (<math>\frac{T}{4}</math> oder <math>\frac{2\, \pi}{4}</math>) verschoben. | |
| − | + | ||
| − | + | Der Graph der Beschleunigung ist gegenüber dem der Auslenkung um eine Halbe Periode (<math>\frac{T}{2}</math> oder <math>\frac{2\, \pi}{2}</math>) verschoben und hat immer ein anderes Vorzeichen als die Auslenkung. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | *Erklären Sie das anhand der Bewegung des Wagens. (Nicht mathematisch über die Ableitung.) | |
| − | + | *Berechnen Sie die maximale Geschwindigkeit <math>\hat v</math> und die maximale Beschleunigung <math>\hat a</math> aus der Winkelgeschwindigkeit <math>\omega</math>. | |
| + | :Kontrollieren Sie ihr Ergebnis an den Graphen von <math>v(t)</math> und <math>a(t)</math>. | ||
| − | + | ====Schwingmännchen II==== | |
| + | Das Männchen schwingt mit einer Auslenkung y von: | ||
| − | + | :<math>y(t)=5\, {\rm cm} \cdot \sin(3\, {\rm Hz} \cdot t)</math> | |
| + | *Wie groß sind Amplitude, Frequenz und Periodendauer? | ||
| − | + | *Zeichnen Sie das Ortsdiagramm, das Geschwindigkeitsdiagramm und das Beschleunigungsdiagramm jeweils in ein Koordinatensystem. | |
| − | + | ||
| − | + | ||
| − | + | *Zeichen Sie zum Ortsdiagramm die Zeiger für die Zeitpunkte t=0 sec, t=0,25 sec und t=1 sec. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | *Lesen Sie an den Diagrammen ab wo das Männchen nach 1,6 Sekunden ist und wie schnell es sich bewegt. | |
| − | + | ||
| − | [[ | + | ====Eine "Schwingungswaage"==== |
| + | [[Datei:Waage_weltraum.jpg|thumb]] | ||
| + | In der International Space Station (ISS) funktionieren die "normalen" Waagen nicht mehr, weil man dort die Gewichtskraft nicht messen kann. Aber trotzdem kann man sich auch dort wiegen! | ||
| − | + | Der Sitz dieser "Weltraumwaage" ist zwischen zwei Federn gespannt und kann so frei schwingen. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | *Erläutern Sie, warum man mit dieser Waage die Masse der Astronautin bestimmen kann. Benutzen Sie hierfür die Begriffe Trägheit und beschleunigende Kraft/Rückstellkraft. | |
| − | + | *Wie verändert sich die Frequenz, wenn man die Amplitude der Schwingung verändert? Warum ist das für die Weltraumwaage sehr praktisch? | |
| − | + | ||
| − | + | Der leere Stuhl hat eine Masse von <math>m_0=2\, \rm kg</math> und schwingt mit einer Periode von <math>T=0{,}33\, \rm s</math>. | |
| − | + | *Bestimmen Sie hieraus die Härte <math>D</math> der Feder. | |
| + | Nun steigt die Astronautin in den Stuhl und die Periodendauer verlängert sich auf <math>T=1{,}87\, \rm s</math>. | ||
| + | *Welche Masse hat die Astronautin? | ||
| − | + | In einem Modellversuch schwingt ein Wagen zwischen zwei Federn. Die Federkonstante einer Feder beträgt D= 3 N/m. Zusammen wirken sie wie eine Feder mit der doppelten Federkonstante. Der Wagen hat eine Masse von 190,6g. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | *Wie schwer ist eine am Wagen befestigte Batterie, wenn der Wagen mit ihr nun in 5,6 Sekunden viermal schwingt? | |
| − | + | ||
| + | (Ein Video mit einer ähnlichen "body mass measurement device" der NASA findet sich [http://www.youtube.com/watch?v=8rt3udip7l4 hier].) | ||
| + | (Auch LEIFI beschäftigt sich [http://www.leifiphysik.de/themenbereiche/mechanische-schwingungen/aufgaben#lightbox=/themenbereiche/mechanische-schwingungen/lb/mechanische-schwingungen-massebestimmung-im-weltall-0 hier] damit.) | ||
| − | + | ====Schaukeltier II==== | |
| + | Große und kleine Kinder schaukeln auf dem gleichen Tier unterschiedlich. Was ist der Unterschied? | ||
| − | + | ====Schwingmännchen III==== | |
| + | [[Datei:Schwingmännchen.jpg|thumb|Eine Schwingprinzessin]] | ||
| + | Das Männchen bringt 200g auf die Waage und verlängert beim Dranhängen die vorher unbelastete Feder um 40cm. | ||
| − | + | *Wieso beträgt die Federkonstante (D) gerade 1/20 N/cm = 0,05 N/cm? | |
| + | *Zeichnen Sie den Zusammenhang von Rückstellkraft und Auslenkung, also den Graphen von <math>F(y)</math> in ein Koordinatensystem. | ||
| − | + | *Mit welcher Frequenz wird das Männchen schwingen? | |
| − | + | Hängt man das Männchen nur an die Hälfte der Feder, so wird bereits bei der halben Auslenkung die entsprechende Kraft erreicht. Die Federkonstante D verdoppelt sich also. Entsprechendes ergibt sich, wenn man zwei Federn aneinander hängt: Die Federkonstante halbiert sich. | |
| − | + | *An welcher Stelle der Feder muss man festhalten, damit sich dadurch die Frequenz verdoppelt? | |
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ==== | + | ====Schwingmännchen IV==== |
| − | + | Wie kann man es erreichen, dass das Männchen "doppelt so schnell", also mit doppelter Frequenz, schwingt? | |
| − | ==== | + | ====Schwingmännchen V==== |
| − | + | Wie verändert sich die Frequenz und die Energie des Männchens, wenn sich | |
| − | + | *die Federkonstante verdoppelt | |
| + | *die Masse verdoppelt | ||
| + | *die Amplitude verdoppelt | ||
| + | und dabei die jeweils anderen Größen unverändert bleiben? | ||
| − | + | ====Schaukeltier III==== | |
| + | Worauf müssen die Kinder beim "Anschubsen" achten? | ||
| + | |||
| + | ====Schwingungskategorien==== | ||
| + | Nennen Sie für jede der verschiedenen Kategorien von Schwingungen ein Beispiel und erläutern Sie es kurz. | ||
| + | *frei | ||
| + | *angeregt | ||
| + | *selbsterregt | ||
| + | *erzwungen | ||
| + | |||
| + | ====Wackelnder Rückspiegel==== | ||
| + | Fahre ich mit meinem Auto ca. 90 km/h , so wackelt der Rückspiegel und das Bild wird dadurch unscharf. | ||
| + | |||
| + | Was könnte ich alles tun, damit der Spiegel aufhört zu schwingen? | ||
| + | |||
| + | ====harmonische Schwingung==== | ||
| + | Woran erkennt man eine "harmonische" Schwingung? | ||
| + | |||
| + | ====Energie==== | ||
| + | Welche Energie hat eine schwingender Körper der Masse 1kg, wenn er eine Periodendauer von 1s und eine Amplitude von 1cm hat? | ||
| + | |||
| + | ====Energie II==== | ||
| + | Wie muss ein Körper der Masse 1kg schwingen, damit die Schwingung 1J Energie hat? | ||
| + | |||
| + | ====Energie III==== | ||
| + | Zwei gleichschwere Körper schwingen mit der gleichen Amplitude, aber der eine doppelt so schnell wie der andere. Vergleichen sie die Energiemengen. | ||
| − | Die | + | ====Zwei schwingende Wagen==== |
| − | + | [[Datei:Schwingende_Wagen.jpg|thumb|Die Wagen stehen auf einer Schiene und sind mit einer Feder verbunden.]] | |
| − | + | Wenn die Wagen schwingen haben sie zu unterschiedlichen Phasen der Schwingung unterschiedlich viel Impuls. Der Impuls nach rechts soll als positiv gewertet werden. | |
| − | + | Ebenso ändert sich die Energiemenge in der Feder und in den Wagen. | |
| − | + | *Ergänze in der Tabelle qualitativ die Angaben von Impuls und Energie. | |
| + | <br style="clear: both" /> | ||
| − | + | {|class="wikitable" | |
| − | + | !Phase | |
| + | !Bild | ||
| + | !colspan="2"|Impuls | ||
| + | !colspan="2"|Energie | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | |width="100px"|links | ||
| + | |width="100px"|rechts | ||
| + | |width="100px"|Feder | ||
| + | |width="100px"|Kugeln | ||
| + | |- | ||
| + | |<math>t=0\,\rm s</math> <br> Ruhelage | ||
| + | |[[Datei:Schwingung zwei Körper Ruhelage.png|497px]] | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |- | ||
| + | |<math>t=\frac{1}{4} \, T </math> <br> innere Umkehrpunkte | ||
| + | |[[Datei:Schwingung zwei Körper Umkehrpunkt innen.png|497px]] | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |- | ||
| + | |<math>t=\frac{1}{2}\, T \,\rm s</math> <br> Ruhelage | ||
| + | |[[Datei:Schwingung zwei Körper Ruhelage.png|497px]] | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |- | ||
| + | |<math>t=\frac{3}{4}\, T </math> <br> äußere Umkehrpunkte | ||
| + | |[[Datei:Schwingung zwei Körper Umkehrpunkt aussen.png|497px]] | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |- | ||
| + | |<math>t=T </math> <br> Ruhelage | ||
| + | |[[Datei:Schwingung zwei Körper Ruhelage.png|497px]] | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |} | ||
| − | ==== | + | ====Wasserstoffmolekül==== |
| − | Ein H<sub>2</sub>-Molekül kann man idealisiert als zwei, mit einer Feder verbundene, Körper auffassen. | + | Ein H<sub>2</sub>-Molekül kann man idealisiert als zwei, mit einer Feder verbundene, Körper auffassen. (So wie [[Energie_und_Impuls_einer_mechanischen_Schwingung#Animation|hier]].) |
Durch eine Messung regt man das Molekül zum Schwingen an und bestimmt die Frequenz der Schwingung zu 9,2 10<sup>11</sup> Hz. | Durch eine Messung regt man das Molekül zum Schwingen an und bestimmt die Frequenz der Schwingung zu 9,2 10<sup>11</sup> Hz. | ||
| Zeile 186: | Zeile 236: | ||
Wieviel Energie steckt im Molekül, wenn beide Atome mit einer Amplitude von 10<sup>-10</sup>m schwingen? | Wieviel Energie steckt im Molekül, wenn beide Atome mit einer Amplitude von 10<sup>-10</sup>m schwingen? | ||
| − | + | (Fehlende Angaben entnehmen sie dem Buch oder dem www.) | |
| − | + | ====Molekül-Spektroskopie==== | |
| − | + | Bei der TransmissionsSpektroskopie bestrahlt man ein Gas oder einen anderen Stoff mit einer elektromagnetischen Welle und führt ihm so Energie mit einer bestimmten Frequenz zu. Auf der anderen Seite wird gemessen, wieviel Energie noch ankommt. Die fehlende Energie ist absorbiert oder in eine andere Richtung abgestrahlt worden. | |
| − | + | ||
| − | + | ||
| − | + | *Bei großen oder langen Molekülen findet man viele Frequenzen, bei denen die Energie nicht auf der anderen Seite ankommt. Bei einem Molekül wie Kohlenmonoxid (CO) nur eine <ref>Das ist etwas vereinfacht, aber es gibt wesentlich weniger Absorptionsfrequenzen.</ref>. Wie kann man das erklären? | |
| − | + | *Bei Kohlenmonoxid misst man eine Absorption bei der Frequenz <math>f=6{,}5\cdot 10^{13}\,\rm Hz</math>. Als Modell für das Molekül kann man vereinfachend zwei punktförmige Massen annehmen, die mit einer masselosen Feder verbunden sind. (So wie [[Energie_und_Impuls_einer_mechanischen_Schwingung#Animation|hier]].) | |
| + | :Bestimmen Sie die "Federkonstante" des Moleküls. | ||
| + | :(Fehlende Angaben finden Sie in Physik- oder Chemiebüchern oder im www.) | ||
| + | ====Schwebung von Stimmgabeln==== | ||
| + | Zwei Stimmgabeln erzeugen eine Schwebung, weil die eine mit einem Reiter versehen wurde. Die Frequenz derjenigen ohne Reiter beträgt 440 Hz, die andere hat eine Frequenz von 438 Hz. | ||
| + | :Was kann man hören? | ||
| + | ====Zeigeraddition bei einer Schwebung==== | ||
| + | Zwei Stimmgabeln bewirken an einem Ort Luftdruckschwankungen des Normaldrucks von: | ||
| + | :<math>p_1(t)=0{,}02\, \rm Pa \cdot \sin(2\pi \cdot 1000\, Hz \cdot t)</math> | ||
| + | :<math>p_2(t)=0{,}01\, \rm Pa \cdot \sin(2\pi \cdot 998\, Hz \cdot t)</math> | ||
| + | *Welche Stimmgabel erzeugt den lauteren Ton, welche den höheren und woran erkennt man das? | ||
| + | *Welche Periode und welche Frequenz haben die beiden Luftschwingungen? | ||
| + | *Wie sehen die Zeiger für die verschiedenen Zeitpunkte aus? | ||
| + | :{| | ||
| + | ||<math>t= 0 \,\rm s</math>||...||<math>t= 1 \,\rm s</math>||...||<math>t= \frac{1}{2} \,\rm s</math>||...||<math>t= \frac{1}{4} \,\rm s</math>||...||<math>t= \frac{3}{4} \,\rm s</math>||...||<math>t= \frac{1}{8} \,\rm s</math> | ||
| + | |} | ||
| + | *Welcher Druck herrscht zu den unterschiedlichen Zeitpunkten? | ||
| + | |||
| + | ====Überlagerung zweier Schwingungen==== | ||
| + | Bestimmen Sie jeweils die Schwingung, die aus der Überlagerung von y<sub>1</sub> und y<sub>2</sub> entsteht mit Hilfe des Zeigerdiagramms: | ||
| + | |||
| + | #<math>y_1 = {\rm 2\, cm} \cdot \sin(2t)\qquad y_2 = {\rm 4 \, cm} \cdot \sin(2t+\pi)</math> | ||
| + | #<math>y_1 = {\rm 2\, cm} \cdot \sin(2t)\qquad y_2 = {\rm 4\, cm} \cdot \sin(2t+\pi/2)</math> | ||
| + | #<math>y_1 = {\rm 2\, cm} \cdot \sin(2t)\qquad y_2 = {\rm 2\, cm} \cdot \sin(2t+\pi)</math> | ||
| + | |||
| + | ==Schwieriges und Anderes== | ||
| + | ====7 Schwingung bei bekannter Energie==== | ||
| + | Zwei Wagen, die beide eine Masse von 600g haben, sind mit einer Feder der Härte 1N/cm verbunden. | ||
| + | Wie schwingen die Wagen, wenn ihnen eine Energie von 1Joule zugeführt wird? | ||
====9 E<sub>kin</sub> = E<sub>Spann</sub>==== | ====9 E<sub>kin</sub> = E<sub>Spann</sub>==== | ||
Für welche Auslenkung verteilt sich die Energie eines (horizontalen) Federpendels gerade je zur Hälfte auf die Feder und den Impuls? | Für welche Auslenkung verteilt sich die Energie eines (horizontalen) Federpendels gerade je zur Hälfte auf die Feder und den Impuls? | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
====10 Zeitlicher Mittelwert von E<sub>kin</sub> und E<sub>Spann</sub>==== | ====10 Zeitlicher Mittelwert von E<sub>kin</sub> und E<sub>Spann</sub>==== | ||
Bestimmen sie das zeitliche Mittel der kinetischen und potentiellen Energie (Spannenergie der Feder) eines (horizontalen) Federpendels an einem selbst gewählten Beispiel. | Bestimmen sie das zeitliche Mittel der kinetischen und potentiellen Energie (Spannenergie der Feder) eines (horizontalen) Federpendels an einem selbst gewählten Beispiel. | ||
| + | Hinweise: | ||
| + | :<math>E_{kin}(t)= \frac{1}{2} m \, v(t)^2 \qquad E_{pot} = \frac{1}{2} D\, y(t)^2</math> | ||
| + | |||
| + | Den Mittelwert einer Funktion f(x) von x<sub>1</sub> bis x<sub>2</sub> bestimmt man mit Hilfe des Integrals: | ||
| + | |||
| + | :<math>\bar f = \frac{1}{t_2 - t_1} \int_{t_1}^{t_2}f(t) dt</math> | ||
| + | |||
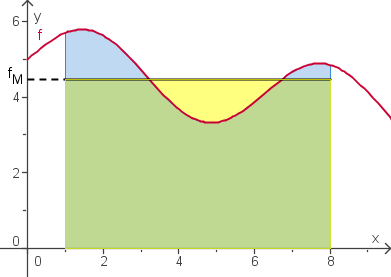
| + | Anschaulich bestimmt man zur Fläche zwischen Schaubild und x-Achse ein Rechteck gleicher Fläche. Die Höhe des Rechtecks ist gerade der Mittelwert. | ||
| + | |||
| + | [[Bild:Mittelwert_einer_Funktion.png|none]] | ||
| + | |||
| + | ==[[Aufgaben zu Schwingungen (Lösungen)|Lösungen]]== | ||
| + | |||
| + | ==Fußnoten== | ||
| + | <references /> | ||
Aktuelle Version vom 7. Oktober 2021, 07:46 Uhr
(Kursstufe > Mechanische Schwingungen)
Inhaltsverzeichnis
- 1 Energieformen
- 2 Schaukeltier
- 3 Zeigermodell
- 4 Uhrzeiger
- 5 Schwingmännchen
- 6 Stimmgabel
- 7 Horizontales Federpendel
- 8 Schwingmännchen II
- 9 Eine "Schwingungswaage"
- 10 Schaukeltier II
- 11 Schwingmännchen III
- 12 Schwingmännchen IV
- 13 Schwingmännchen V
- 14 Schaukeltier III
- 15 Schwingungskategorien
- 16 Wackelnder Rückspiegel
- 17 harmonische Schwingung
- 18 Energie
- 19 Energie II
- 20 Energie III
- 21 Zwei schwingende Wagen
- 22 Wasserstoffmolekül
- 23 Molekül-Spektroskopie
- 24 Schwebung von Stimmgabeln
- 25 Zeigeraddition bei einer Schwebung
- 26 Überlagerung zweier Schwingungen
- 27 Schwieriges und Anderes
- 28 Lösungen
- 29 Fußnoten
Energieformen
Nennen Sie zwei verschiedene Beispiele für eine Schwingung und beschreiben Sie kurz wann dabei welche Energieformen auftreten.
Schaukeltier
Ein Kind "reitet" auf einem Feder-Schaukeltier. Erklären Sie anhand dieses Beispiels die Begriffe:
- Ruhelage
- Elongation
- Amplitude
- Rückstellkraft
- Periodendauer
- Frequenz
Nennen Sie noch ein weiteres Beispiel für eine mechanische Schwingung und machen Sie sich wiederum diese Begriffe klar.
Zeigermodell
Wie kann man eine harmonische Schwingung mit einem Zeiger beschreiben?
Beschreiben Sie dazu den im Unterricht durchgeführten Versuch.
Uhrzeiger
Eine Uhr hat einen Stunden-, einen Minuten- und einen Sekundenzeiger.
- Begründen Sie warum der Sekundenzeiger eine Winkelgeschwindigkeit von [math]\omega = \frac{2\, \pi}{60\, \rm s}[/math] hat.
- Welche Frequenz und welche Periodendauer hat der Sekundenzeiger?
- Mit welcher Geschwindigkeit [math]v[/math] bewegt sich die Spitze des Sekundenzeigers, wenn er 10cm lang ist?
- Suchen Sie eine Armbanduhr oder eine Wanduhr und bestimmen Sie für alle drei Zeiger die Größen: [math]\omega[/math], [math]f[/math], [math]T[/math] und [math]v[/math].
Schwingmännchen
Ein Schwingmännchen schwingt mit einer Periodendauer von [math]\rm T = 0{,}5\, s[/math] und einer Amplitude von [math]\hat y = \rm 3\, cm[/math].
Die Zeit [math]t[/math] wird ab dem Durchgang von unten nach oben durch die Ruhelage gemessen.
- Zeichnen Sie für folgende Zeitpunkte den Zeiger in ein Koordinatensystem: [math]t_1 = 0{,}25\, s[/math], [math]t_2 = 0{,}125\, s[/math], [math]t_3 = 0{,}4375\, s[/math]
- Bestimmen Sie zeichnerisch jeweils die Auslenkungen [math]y(t_i)[/math].
Stimmgabel
Die Zinken einer Stimmgabel schwingen mit einer Frequenz von 440 Hz[1] und durch eine Messung an einer verußten Glasplatte bestimmt man die größte Amplitude zu [math]\hat y = 2 \, \rm mm[/math].
- Welche Periodendauer und welche Winkelgeschwindigkeit hat die Schwingung?
- Stellen Sie für einen Zinken der Stimmgabel die Bewegungsgleichungen auf:
- [math]y(t)[/math], [math]v(t)[/math], [math]a(t)[/math],
- Bestimmen Sie daraus die maximale Geschwindigkeit und die maximale Beschleunigug eines Zinkens der Stimmgabel.
Horizontales Federpendel
|
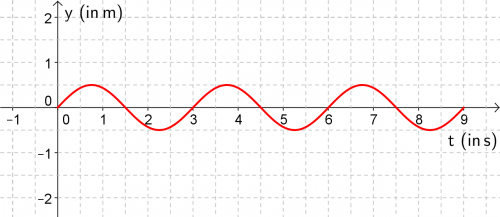
Ein Wagen schwingt horizontal an einer Feder. Die folgenden Graphen beschreiben den Verlauf seiner Bewegung im Koordinatensystem: |
|
- Woran kann man erkennen, dass die Schwingung nicht gedämpft ist, also keine Energie verliert?
- Wie wurde dem Wagen zu Beginn Energie zugeführt? Wurde er ausgelenkt und losgelassen? (und wenn ja, in welche Richtung?) Wurde er angeschubst? (und wenn ja, in welche Richtung?)
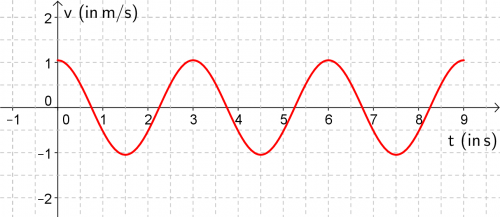
Der Graph der Geschwindigkeit ist gegenüber dem der Auslenkung um eine Viertel Periode ([math]\frac{T}{4}[/math] oder [math]\frac{2\, \pi}{4}[/math]) verschoben.
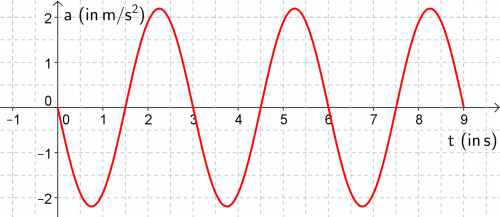
Der Graph der Beschleunigung ist gegenüber dem der Auslenkung um eine Halbe Periode ([math]\frac{T}{2}[/math] oder [math]\frac{2\, \pi}{2}[/math]) verschoben und hat immer ein anderes Vorzeichen als die Auslenkung.
- Erklären Sie das anhand der Bewegung des Wagens. (Nicht mathematisch über die Ableitung.)
- Berechnen Sie die maximale Geschwindigkeit [math]\hat v[/math] und die maximale Beschleunigung [math]\hat a[/math] aus der Winkelgeschwindigkeit [math]\omega[/math].
- Kontrollieren Sie ihr Ergebnis an den Graphen von [math]v(t)[/math] und [math]a(t)[/math].
Schwingmännchen II
Das Männchen schwingt mit einer Auslenkung y von:
- [math]y(t)=5\, {\rm cm} \cdot \sin(3\, {\rm Hz} \cdot t)[/math]
- Wie groß sind Amplitude, Frequenz und Periodendauer?
- Zeichnen Sie das Ortsdiagramm, das Geschwindigkeitsdiagramm und das Beschleunigungsdiagramm jeweils in ein Koordinatensystem.
- Zeichen Sie zum Ortsdiagramm die Zeiger für die Zeitpunkte t=0 sec, t=0,25 sec und t=1 sec.
- Lesen Sie an den Diagrammen ab wo das Männchen nach 1,6 Sekunden ist und wie schnell es sich bewegt.
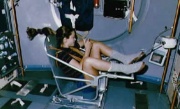
Eine "Schwingungswaage"
In der International Space Station (ISS) funktionieren die "normalen" Waagen nicht mehr, weil man dort die Gewichtskraft nicht messen kann. Aber trotzdem kann man sich auch dort wiegen!
Der Sitz dieser "Weltraumwaage" ist zwischen zwei Federn gespannt und kann so frei schwingen.
- Erläutern Sie, warum man mit dieser Waage die Masse der Astronautin bestimmen kann. Benutzen Sie hierfür die Begriffe Trägheit und beschleunigende Kraft/Rückstellkraft.
- Wie verändert sich die Frequenz, wenn man die Amplitude der Schwingung verändert? Warum ist das für die Weltraumwaage sehr praktisch?
Der leere Stuhl hat eine Masse von [math]m_0=2\, \rm kg[/math] und schwingt mit einer Periode von [math]T=0{,}33\, \rm s[/math].
- Bestimmen Sie hieraus die Härte [math]D[/math] der Feder.
Nun steigt die Astronautin in den Stuhl und die Periodendauer verlängert sich auf [math]T=1{,}87\, \rm s[/math].
- Welche Masse hat die Astronautin?
In einem Modellversuch schwingt ein Wagen zwischen zwei Federn. Die Federkonstante einer Feder beträgt D= 3 N/m. Zusammen wirken sie wie eine Feder mit der doppelten Federkonstante. Der Wagen hat eine Masse von 190,6g.
- Wie schwer ist eine am Wagen befestigte Batterie, wenn der Wagen mit ihr nun in 5,6 Sekunden viermal schwingt?
(Ein Video mit einer ähnlichen "body mass measurement device" der NASA findet sich hier.) (Auch LEIFI beschäftigt sich hier damit.)
Schaukeltier II
Große und kleine Kinder schaukeln auf dem gleichen Tier unterschiedlich. Was ist der Unterschied?
Schwingmännchen III
Das Männchen bringt 200g auf die Waage und verlängert beim Dranhängen die vorher unbelastete Feder um 40cm.
- Wieso beträgt die Federkonstante (D) gerade 1/20 N/cm = 0,05 N/cm?
- Zeichnen Sie den Zusammenhang von Rückstellkraft und Auslenkung, also den Graphen von [math]F(y)[/math] in ein Koordinatensystem.
- Mit welcher Frequenz wird das Männchen schwingen?
Hängt man das Männchen nur an die Hälfte der Feder, so wird bereits bei der halben Auslenkung die entsprechende Kraft erreicht. Die Federkonstante D verdoppelt sich also. Entsprechendes ergibt sich, wenn man zwei Federn aneinander hängt: Die Federkonstante halbiert sich.
- An welcher Stelle der Feder muss man festhalten, damit sich dadurch die Frequenz verdoppelt?
Schwingmännchen IV
Wie kann man es erreichen, dass das Männchen "doppelt so schnell", also mit doppelter Frequenz, schwingt?
Schwingmännchen V
Wie verändert sich die Frequenz und die Energie des Männchens, wenn sich
- die Federkonstante verdoppelt
- die Masse verdoppelt
- die Amplitude verdoppelt
und dabei die jeweils anderen Größen unverändert bleiben?
Schaukeltier III
Worauf müssen die Kinder beim "Anschubsen" achten?
Schwingungskategorien
Nennen Sie für jede der verschiedenen Kategorien von Schwingungen ein Beispiel und erläutern Sie es kurz.
- frei
- angeregt
- selbsterregt
- erzwungen
Wackelnder Rückspiegel
Fahre ich mit meinem Auto ca. 90 km/h , so wackelt der Rückspiegel und das Bild wird dadurch unscharf.
Was könnte ich alles tun, damit der Spiegel aufhört zu schwingen?
harmonische Schwingung
Woran erkennt man eine "harmonische" Schwingung?
Energie
Welche Energie hat eine schwingender Körper der Masse 1kg, wenn er eine Periodendauer von 1s und eine Amplitude von 1cm hat?
Energie II
Wie muss ein Körper der Masse 1kg schwingen, damit die Schwingung 1J Energie hat?
Energie III
Zwei gleichschwere Körper schwingen mit der gleichen Amplitude, aber der eine doppelt so schnell wie der andere. Vergleichen sie die Energiemengen.
Zwei schwingende Wagen
Wenn die Wagen schwingen haben sie zu unterschiedlichen Phasen der Schwingung unterschiedlich viel Impuls. Der Impuls nach rechts soll als positiv gewertet werden.
Ebenso ändert sich die Energiemenge in der Feder und in den Wagen.
- Ergänze in der Tabelle qualitativ die Angaben von Impuls und Energie.
Wasserstoffmolekül
Ein H2-Molekül kann man idealisiert als zwei, mit einer Feder verbundene, Körper auffassen. (So wie hier.) Durch eine Messung regt man das Molekül zum Schwingen an und bestimmt die Frequenz der Schwingung zu 9,2 1011 Hz.
Bestimmen sie die "Federkonstante" der gedachten Feder zwischen den Molekülen. Wieviel Energie steckt im Molekül, wenn beide Atome mit einer Amplitude von 10-10m schwingen?
(Fehlende Angaben entnehmen sie dem Buch oder dem www.)
Molekül-Spektroskopie
Bei der TransmissionsSpektroskopie bestrahlt man ein Gas oder einen anderen Stoff mit einer elektromagnetischen Welle und führt ihm so Energie mit einer bestimmten Frequenz zu. Auf der anderen Seite wird gemessen, wieviel Energie noch ankommt. Die fehlende Energie ist absorbiert oder in eine andere Richtung abgestrahlt worden.
- Bei großen oder langen Molekülen findet man viele Frequenzen, bei denen die Energie nicht auf der anderen Seite ankommt. Bei einem Molekül wie Kohlenmonoxid (CO) nur eine [2]. Wie kann man das erklären?
- Bei Kohlenmonoxid misst man eine Absorption bei der Frequenz [math]f=6{,}5\cdot 10^{13}\,\rm Hz[/math]. Als Modell für das Molekül kann man vereinfachend zwei punktförmige Massen annehmen, die mit einer masselosen Feder verbunden sind. (So wie hier.)
- Bestimmen Sie die "Federkonstante" des Moleküls.
- (Fehlende Angaben finden Sie in Physik- oder Chemiebüchern oder im www.)
Schwebung von Stimmgabeln
Zwei Stimmgabeln erzeugen eine Schwebung, weil die eine mit einem Reiter versehen wurde. Die Frequenz derjenigen ohne Reiter beträgt 440 Hz, die andere hat eine Frequenz von 438 Hz.
- Was kann man hören?
Zeigeraddition bei einer Schwebung
Zwei Stimmgabeln bewirken an einem Ort Luftdruckschwankungen des Normaldrucks von:
- [math]p_1(t)=0{,}02\, \rm Pa \cdot \sin(2\pi \cdot 1000\, Hz \cdot t)[/math]
- [math]p_2(t)=0{,}01\, \rm Pa \cdot \sin(2\pi \cdot 998\, Hz \cdot t)[/math]
- Welche Stimmgabel erzeugt den lauteren Ton, welche den höheren und woran erkennt man das?
- Welche Periode und welche Frequenz haben die beiden Luftschwingungen?
- Wie sehen die Zeiger für die verschiedenen Zeitpunkte aus?
[math]t= 0 \,\rm s[/math] ... [math]t= 1 \,\rm s[/math] ... [math]t= \frac{1}{2} \,\rm s[/math] ... [math]t= \frac{1}{4} \,\rm s[/math] ... [math]t= \frac{3}{4} \,\rm s[/math] ... [math]t= \frac{1}{8} \,\rm s[/math]
- Welcher Druck herrscht zu den unterschiedlichen Zeitpunkten?
Überlagerung zweier Schwingungen
Bestimmen Sie jeweils die Schwingung, die aus der Überlagerung von y1 und y2 entsteht mit Hilfe des Zeigerdiagramms:
- [math]y_1 = {\rm 2\, cm} \cdot \sin(2t)\qquad y_2 = {\rm 4 \, cm} \cdot \sin(2t+\pi)[/math]
- [math]y_1 = {\rm 2\, cm} \cdot \sin(2t)\qquad y_2 = {\rm 4\, cm} \cdot \sin(2t+\pi/2)[/math]
- [math]y_1 = {\rm 2\, cm} \cdot \sin(2t)\qquad y_2 = {\rm 2\, cm} \cdot \sin(2t+\pi)[/math]
Schwieriges und Anderes
7 Schwingung bei bekannter Energie
Zwei Wagen, die beide eine Masse von 600g haben, sind mit einer Feder der Härte 1N/cm verbunden. Wie schwingen die Wagen, wenn ihnen eine Energie von 1Joule zugeführt wird?
9 Ekin = ESpann
Für welche Auslenkung verteilt sich die Energie eines (horizontalen) Federpendels gerade je zur Hälfte auf die Feder und den Impuls?
10 Zeitlicher Mittelwert von Ekin und ESpann
Bestimmen sie das zeitliche Mittel der kinetischen und potentiellen Energie (Spannenergie der Feder) eines (horizontalen) Federpendels an einem selbst gewählten Beispiel. Hinweise:
- [math]E_{kin}(t)= \frac{1}{2} m \, v(t)^2 \qquad E_{pot} = \frac{1}{2} D\, y(t)^2[/math]
Den Mittelwert einer Funktion f(x) von x1 bis x2 bestimmt man mit Hilfe des Integrals:
- [math]\bar f = \frac{1}{t_2 - t_1} \int_{t_1}^{t_2}f(t) dt[/math]
Anschaulich bestimmt man zur Fläche zwischen Schaubild und x-Achse ein Rechteck gleicher Fläche. Die Höhe des Rechtecks ist gerade der Mittelwert.
Lösungen
Fußnoten
- ↑ Das ist der Kammerton a. (Siehe auch Wikipedia: Kammerton)
- ↑ Das ist etwas vereinfacht, aber es gibt wesentlich weniger Absorptionsfrequenzen.