|
|
| Zeile 4: |
Zeile 4: |
| | |height="800x"| | | |height="800x"| |
| | | | |
| | + | |} |
| | + | ==Übersicht== |
| | + | Je nach der Art der Energiezufuhr oder des Verlustes kann man Schwingungen in verschiedene Kategorien einteilen: |
| | + | ====Energieabgabe==== |
| | + | {| |
| | + | |valign="top"| |
| | + | ;gedämpfte und ungedämpfte Schwingungen |
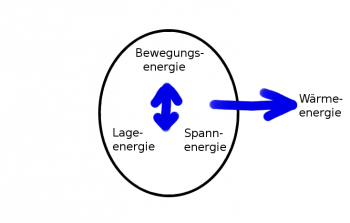
| | + | :Gedämpfte Schwingungen verlieren Energie an die Umgebung, dabei nimmt die Amplitude ab. Bei allen realen mechanischen Schwingungen tritt Reibung auf, weshalb alle Schwingungen auch mehr oder weniger stark gedämpft sind. |
| | + | | |
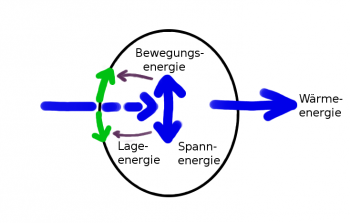
| | + | [[Datei:Schwingungen_schematisch_nach_Energiezufuhr_gedämpft.png|thumb|none|350px|Energieflußdiagramm einer freien, gedämpften Schwingung.]] |
| | + | |- |
| | + | |valign="top"| |
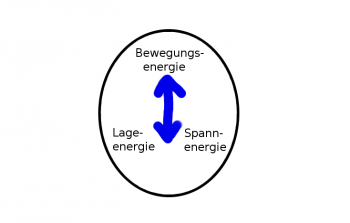
| | + | :Ungedämpfte Schwingungen ohne Energieabgabe gibt es in Reinform nur als abstrakte Idee, da es eine reibungslose Bewegung nicht gibt. Nur durch ständige Energiezufuhr kann erreicht werden, dass die Energiemenge der Schwingung, und somit auch die Amplitude, konstant bleibt. |
| | + | | |
| | + | [[Datei:Schwingungen_schematisch_nach_Energiezufuhr_ungedämpft.png|thumb|none|350px|Energieflußdiagramm einer freien, ungedämpften Schwingung.]] |
| | |} | | |} |
| | | | |
| − | =Fehlerrechnung= | + | ====Energiezufuhr==== |
| − | ==Systematische und zufällige Messfehler== | + | {| |
| − | | + | |valign="top"| |
| − | *Jede Messung ermittelt nur einen ungenauen Wert einer Größe.
| + | ; freie Schwingungen |
| − | *Dabei enthaltene Messfehler teilt man in systematische und zufällige Fehler ein.
| + | : Bei einer freien Schwingung wird von Außen gar keine Energie zugeführt. Man beeinflußt die Schwingung nicht. |
| − | :Systematische Fehler entstehen z.B. durch einen falschen Versuchsaufbau. Sie verschieben die gemessenen Werte um einen festen Betrag. Sie sind schwer abzuschätzen oder zu korrigieren. | + | |- |
| − | :Bei zufälligen Fehlern geht man davon aus, dass die Messwerte um den korrekten Wert schwanken. Zufällige Fehler werden durch Schwankungen der Messgröße, der Messgeräte, der Umwelt, durch den Beobachter etc. verursacht. Sie sind unvermeidbar, können aber abgeschätzt und durch Wiederholung verringert werden. Dazu verwendet man die Statistik. | + | |valign="top"| |
| − | | + | ; erzwungene und angeregte Schwingungen |
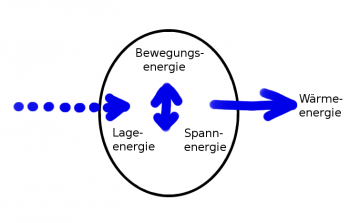
| − | :{| | + | : Bei einer erzwungenen Schwingung wird durch eine periodische Anregung die Frequenz der Schwingung festgelegt. Je nachdem wie gut die Anregungsfrequenz "paßt", nimmt die Schwingung mehr oder weniger Energie auf. |
| − | <gallery widths=162px heights=162px perrow=2 caption="Graphische Veranschaulichung der Fehlertypen">
| + | :Beispiele sind Vibrationen beim Auto, die bei bestimmten Geschwindigkeiten auftreten. |
| − | Bild:Fehlerdarstellung Zielscheibe systematisch-klein zufällig-klein.png|Kleiner zufälliger Fehler<br/>Kleiner systematischer Fehler
| + | | |
| − | Bild:Fehlerdarstellung Zielscheibe systematisch-groß zufällig-klein.png|Kleiner zufälliger Fehler<br/>Großer systematischer Fehler
| + | [[Datei:Schwingungen_schematisch_nach_Energiezufuhr_erzwungen.png|thumb|none|350px|Energieflußdiagramm einer erzwungenen, gedämpften Schwingung.]] |
| − | Bild:Fehlerdarstellung Zielscheibe systematisch-klein zufällig-groß.png|Großer zufälliger Fehler<br/>Kleiner systematischer Fehler
| + | |- |
| − | Bild:Fehlerdarstellung Zielscheibe systematisch-groß zufällig-groß.png|Großer zufälliger Fehler<br/>Großer systematischer Fehler
| + | |valign="top"| |
| − | </gallery>
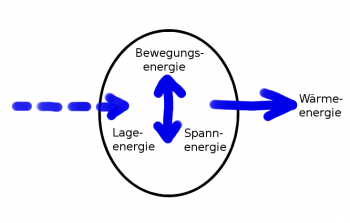
| + | :Erfolgt die Energiezufuhr in der Eigenfrequenz, spricht man von einer angeregten Schwingung. Eine angeregte Schwingung ist also einer erzwungene Schwingung in der "passenden" Frequenz. |
| | + | :Durch die Energiezufuhr wird die Dämpfung quasi aufgehoben, aber die Frequenz nicht vorgegeben. Die Schwingung verhält sich wie eine freie, ungedämpfte Schwingung. |
| | + | :Beispiele sind Kinderschaukeln, die Unruhe oder das Pendel einer mechanischen Uhr und der Schwingquarz bei einer Quarzuhr. |
| | + | | |
| | + | [[Datei:Schwingungen_schematisch_nach_Energiezufuhr_angeregt.png|thumb|none|350px|Energieflußdiagramm einer angeregten, gedämpften Schwingung.]] |
| | + | |- |
| | + | |valign="top"| |
| | + | ; selbsterregte Schwingungen: So bezeichnet man angeregte Schwingungen, bei denen die Steuerung der Energiezufuhr durch das vorgegebene System selbst geschieht. |
| | + | :Beispiele sind die Selbsterregung von im Wind wackelnden Blättern ("Espenlaub"), das Streichen einer Violinsaite mit dem Bogen oder die menschliche Stimme. Eine Uhr als Ganzes führt auch eine selbsterregte Schwingung durch, denn das Uhrwerk steuert selbst die Energiezufuhr. |
| | + | | |
| | + | [[Datei:Schwingungen_schematisch_nach_Energiezufuhr_selbsterregt.png|thumb|none|350px|Energieflußdiagramm einer selbsterregten, gedämpften Schwingung.]] |
| | |} | | |} |
| − |
| |
| − | ==Angabe von Messfehlern==
| |
| − | *Als absolute Angabe mit Einheiten: <math>l=2\,\rm m \ (\pm 0,01\,\rm m) \qquad \qquad l = l_0 \pm \Delta l</math>
| |
| − | *Als relative Angabe ohne Einheiten: <math>l=2\,\rm m \ (\pm 0,05)\ (\pm 5 \%) \qquad (\pm \frac{\Delta l}{l})</math>
| |
| − | *Mit Hilfe von geltenden Ziffern, wobei nur die letzte Ziffer fehlerbehaftet ist: <math>l=2,000\,\rm m</math>
| |
| − |
| |
| − | ==Statistische Beurteilung von zufälligen Fehlern==
| |
| − |
| |
| − | *Dazu müssen eine möglichst große Anzahl von <math>N</math> Messungen der gleichen Größe <math>x</math> durchgeführt werden.
| |
| − | [[Bild:Gausskurve_sw.jpg|thumb|Gaußsche Glockenkurve]]
| |
| − | *Häufig kann man annehmen, dass der Messwert normalverteilt ist, die Häufigkeiten also der Gaußschen Glockenkurve entsprechen. (Das liegt daran, dass eine zufällige Größe, die von sehr vielen voneinander unabhängigen Einflüssen abhängt, normalverteilt ist. (Sogenannter "zentraler Grenzwertsatz"))
| |
| − |
| |
| − | *Der Verlauf der Kurve und damit die Messwerte werden durch die Angabe des Mittelwerts (<math>\bar x</math>) und der Standardabweichung (<math>s</math> oder <math>\sigma</math>) vollständig festgelegt. Der Mittelwert gibt den Ort des Maximums an, die Standardabweichung gibt den Abstand der Wendestellen von der Extremstelle an.
| |
| − |
| |
| − | :<math>\bar x = \frac{\sum_{i=1}^N x_i}{N} \qquad \sigma = s = \sqrt{\frac{\sum_{i=1}^N (\bar x - x_i)^2}{N-1}}</math>
| |
| − |
| |
| − | [[Bild:Gausskurve_mit_Vertrauensgrenzen.jpg|thumb|Gausskurve mit Vertrauengrenzen]]
| |
| − | *Die Standardabweichung der Messwerte gibt an, wie genau die Messungen waren. Kleine Abweichung = Genaue Messung. Man kann damit auch die Wahrscheinlichkeit angeben, dass ein Messwert innerhalb eines Bereichs liegt.
| |
| − | Maximale absolute Abweichung | Vertrauensniveau
| |
| − | s | 68% (ca. 2/3)
| |
| − | 2 s | 95%
| |
| − | 2,5 s | 99%
| |
| − | *Für das Gesamtergebnis ist aber nicht der einzelne Messwert, sondern der Mittelwert der N Messwerte interessant. Dies berücksichtigt dann auch die Tatsache, dass der Mittelwert immer weniger unsicher wird, je mehr Messungen durchgeführt werden!
| |
| − |
| |
| − | :Für den Mittelwert gibt es auch eine Wahrscheinlichkeitsverteilung mit einer anderen Glockenkurve. Daraus ergibt sich die Standardabweichung des Mittelwertes <math>s_M</math>. Sie ergibt eine Abschätzung für den Fehler des Mittelwertes und wird als '''Fehler der Messung''' angegeben.
| |
| − |
| |
| − | :<math>s_M = \frac{s}{\sqrt{N}}</math>
| |
| − | :Mit einer Wahrscheinlichkeit von 68% liegt also der Mittelwert der N Messungen im Bereich <math>\bar x \pm s_M</math>.
| |
| − |
| |
| − |
| |
| − | ==Fehlerfortpflanzung==
| |
| − | *Häufig werden eine oder mehrere fehlerbehaftete Ergebnisse verwendet, um ein Gesamtergebnis zu berechnen, das natürlich auch fehlerbehaftet ist. Man spricht von Fehlerfortpflanzung.
| |
| − |
| |
| − | ===Summen und Differenzen===
| |
| − | *Die absoluten Fehler addieren sich.
| |
| − | ;Beispiel:
| |
| − | Es wird die Dicke eines Blatt Papiers zu <math>0{,}2\,\rm mm \ (\pm 0{,}01\,\rm mm)</math> bestimmt. Für die Dicke von 50 Blättern ergibt sich: <math>10\,\rm mm \ (\pm 0{,}5\,\rm mm)</math>
| |
| − |
| |
| − | ===Produkte und Quotienten===
| |
| − | *Die relativen Fehler addieren sich.
| |
| − | '''Beispiel:'''
| |
| − | Zur Bestimmung der Geschwindigkeit wurde die Strecke und die Zeit gemessen:
| |
| − |
| |
| − | :<math>s = 5\,\rm m \ (\pm 0{,}01 \,\rm m) \ (\pm 0{,}2\%)</math>
| |
| − |
| |
| − | :<math>t = 2 \,\rm s \ (\pm 0{,}1 \,\rm s) \ (\pm 5\%)</math>
| |
| − |
| |
| − | :<math>v=\frac{s}{t}= 2{,}5 \,\rm m/s \ (\pm 5{,}2\%)</math>
| |
| − |
| |
| − | Aus dem relativen Fehler ist es nun auch möglich wieder den absoluten Fehler zu berechnen.
| |
| − |
| |
| − | ===Potenzen und Wurzeln===
| |
| − | *Die relativen Fehler werden mit der Potenz gewichtet und addiert.
| |
| − | ;Beispiel:
| |
| − | Bestimmung der kinetischen Energie eines Radfahrers.
| |
| − | :<math>
| |
| − | \begin{alignat}{2}
| |
| − | E_{kin} &= \frac{1}{2}\, m\, v^2 & \qquad (v \textrm{ in } \rm\frac{m}{s} )\\
| |
| − | &= \frac{1}{2}\, m\, \frac{v^2}{3{,}6^2} & \qquad (v \textrm{ in } \rm\frac{km}{h} )
| |
| − | \end{alignat}
| |
| − | </math>
| |
| − | :<math>m = 85,3\,\rm kg \ (\pm 0,1\,\rm kg) \ (\pm 0{,}12\%)</math>
| |
| − | :<math>v = 18\,\rm \frac{km}{h} \ (\pm 1 \,\rm\frac{km}{h}) \ (\pm 5{,}6\%) </math>
| |
| − |
| |
| − | Der relative Messfehler der Geschwindigkeit wird nun doppelt gewichtet (mit zwei multipliziert):
| |
| − | :<math>E_{kin} = 1066{,}66\,\rm J \ (\pm 11{,}32\%)</math>
| |
| − | Um diese Messung zu verbessern, muss man vor allem die Geschwindigkeit genauer messen.
| |
| − |
| |
| − | ;Beispiel:
| |
| − | Bestimmung der Periodendauer eines Pendels.
| |
| − |
| |
| − | :<math>T = 2\pi \, \frac{\sqrt{l}}{\sqrt{g}} = 2\pi \, \frac{l^{1/2}}{g^{1/2}}</math>
| |
| − |
| |
| − | :<math>l = 0{,}6\,\rm m \ (\pm 0{,}1\%)</math>
| |
| − |
| |
| − | :<math>g = 9{,}81 \,\rm m/s^2 \ (\pm 0{,}01\%)</math>
| |
| − |
| |
| − | Die relativen Messfehler werden nun mit 1/2 gewichtet (multipliziert) und addiert:
| |
| − |
| |
| − | :<math>T = 1{,}5539 s \ (\pm 0,055\%)</math>
| |
| − |
| |
| − | In diesem Fall ist also der Gesamtfehler kleiner als der größte Einzelfehler!
| |
Je nach der Art der Energiezufuhr oder des Verlustes kann man Schwingungen in verschiedene Kategorien einteilen: