Messunsicherheit und Fehlerrechnung: Unterschied zwischen den Versionen
(→Statistische Beurteilung von zufälligen Fehlern) |
K (→Wie lang ist das Zimmer?) |
||
| (8 dazwischenliegende Versionen des gleichen Benutzers werden nicht angezeigt) | |||
| Zeile 5: | Zeile 5: | ||
Zunächst schätzen wir die Länge. | Zunächst schätzen wir die Länge. | ||
| − | Zur Messung verwenden wir Zollstöcke. | + | Zur Messung verwenden wir Zollstöcke. Mit einem Zollstock kann man die Länge bis auf einen halben Zentimeter genau ablesen. |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| + | Hier die Urliste der Daten: | ||
| + | Messergebnisse in Metern: | ||
| + | 10,5 | 11,04 | 11,06 | 11,09 | 11,07 | 11,09 | | ||
| + | 11,05 | 10,7 | 11,07 | 11,00 | 11,045 | 11,64 | | ||
| + | Manche Längen kommen häufiger vor als andere, hier die sortierte Liste: | ||
| + | 10,5 | 10,7 | 11,00 | 11,04 | 11,045 | 11,05 | 11,06 | 11,64 | 11,07 | 11,07 | 11,09 | 11,09 | | ||
| + | Um die Häufigkeit eines Messwertes angeben zu können, teilt man den Messbereich in Klassen ein und gibt die Anzahl der Messwerte in dieser Klasse an: | ||
| + | Bereich | Häufigkeit | ||
| + | 10,5 <= x < 11 | 2 | ||
| + | 11 <= x < 11,5 | 9 | ||
| + | 11,5 <= x < 12 | 1 | ||
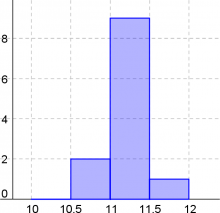
Und das entsprechende Häufigkeitsdiagramm: | Und das entsprechende Häufigkeitsdiagramm: | ||
| − | + | :[[Datei:Histogramm Zimmerlänge.png|220px|none]] | |
Auffällig ist, dass Werte abseits des Mittelwertes weniger häufig auftreten. Bei einer Messung treten also oft Werte um den Mittelwert auf. | Auffällig ist, dass Werte abseits des Mittelwertes weniger häufig auftreten. Bei einer Messung treten also oft Werte um den Mittelwert auf. | ||
Es ist deshalb naheliegend, den Mittelwert der Messwerte als vermutliche Länge des Zimmers zu nehmen: | Es ist deshalb naheliegend, den Mittelwert der Messwerte als vermutliche Länge des Zimmers zu nehmen: | ||
| − | + | :<math>\bar l = 11{,}03 \,\rm m</math> | |
Aber wie genau ist nun unsere Messung? Auf den Millimeter? Oder doch nur +/- einen Zentimeter? | Aber wie genau ist nun unsere Messung? Auf den Millimeter? Oder doch nur +/- einen Zentimeter? | ||
| Zeile 30: | Zeile 36: | ||
==Systematische und zufällige Messfehler== | ==Systematische und zufällige Messfehler== | ||
| − | *Jede Messung | + | *Jede Messung ermittelt nur einen ungenauen Wert einer Größe. |
| − | *Dabei | + | *Dabei enthaltene Messfehler teilt man in systematische und zufällige Fehler ein. |
| − | : | + | :Systematische Fehler entstehen z.B. durch einen falschen Versuchsaufbau. Sie verschieben die gemessenen Werte um einen festen Betrag. Sie sind schwer abzuschätzen oder zu korrigieren. |
| − | :Bei zufälligen Fehlern geht man davon aus, dass die Messwerte um den korrekten Wert schwanken. | + | :Bei zufälligen Fehlern geht man davon aus, dass die Messwerte um den korrekten Wert schwanken. Zufällige Fehler werden durch Schwankungen der Messgröße, der Messgeräte, der Umwelt, durch den Beobachter etc. verursacht. Sie sind unvermeidbar, können aber abgeschätzt und durch Wiederholung verringert werden. Dazu verwendet man die Statistik. |
| − | + | ||
| + | :{| | ||
| + | <gallery widths=162px heights=162px perrow=2 caption="Graphische Veranschaulichung der Fehlertypen"> | ||
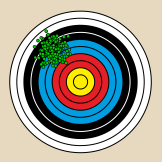
| + | Bild:Fehlerdarstellung Zielscheibe systematisch-klein zufällig-klein.png|Kleiner zufälliger Fehler<br/>Kleiner systematischer Fehler | ||
| + | Bild:Fehlerdarstellung Zielscheibe systematisch-groß zufällig-klein.png|Kleiner zufälliger Fehler<br/>Großer systematischer Fehler | ||
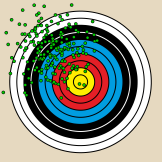
| + | Bild:Fehlerdarstellung Zielscheibe systematisch-klein zufällig-groß.png|Großer zufälliger Fehler<br/>Kleiner systematischer Fehler | ||
| + | Bild:Fehlerdarstellung Zielscheibe systematisch-groß zufällig-groß.png|Großer zufälliger Fehler<br/>Großer systematischer Fehler | ||
| + | </gallery> | ||
| + | |} | ||
==Angabe von Messfehlern== | ==Angabe von Messfehlern== | ||
| − | *Als absolute Angabe mit Einheiten: <math>l= | + | *Als absolute Angabe mit Einheiten: <math>l=2\,\rm m \ (\pm 0,01\,\rm m) \qquad \qquad l = l_0 \pm \Delta l</math> |
| − | *Als relative Angabe ohne Einheiten: <math>l= | + | *Als relative Angabe ohne Einheiten: <math>l=2\,\rm m \ (\pm 0,05)\ (\pm 5 \%) \qquad (\pm \frac{\Delta l}{l})</math> |
| − | *Mit Hilfe von geltenden Ziffern, wobei nur die letzte Ziffer fehlerbehaftet ist: <math>l=2, | + | *Mit Hilfe von geltenden Ziffern, wobei nur die letzte Ziffer fehlerbehaftet ist: <math>l=2,000\,\rm m</math> |
==Statistische Beurteilung von zufälligen Fehlern== | ==Statistische Beurteilung von zufälligen Fehlern== | ||
| Zeile 96: | Zeile 110: | ||
===Summen und Differenzen=== | ===Summen und Differenzen=== | ||
*Die absoluten Fehler addieren sich. | *Die absoluten Fehler addieren sich. | ||
| − | + | ;Beispiel: | |
| − | Es wird die Dicke eines Blatt Papiers zu <math>0,2 mm (\pm 0, | + | Es wird die Dicke eines Blatt Papiers zu <math>0{,}2\,\rm mm \ (\pm 0{,}01\,\rm mm)</math> bestimmt. Für die Dicke von 50 Blättern ergibt sich: <math>10\,\rm mm \ (\pm 0{,}5\,\rm mm)</math> |
===Produkte und Quotienten=== | ===Produkte und Quotienten=== | ||
| Zeile 104: | Zeile 118: | ||
Zur Bestimmung der Geschwindigkeit wurde die Strecke und die Zeit gemessen: | Zur Bestimmung der Geschwindigkeit wurde die Strecke und die Zeit gemessen: | ||
| − | :<math>s = 5 m (\pm 0,01 | + | :<math>s = 5\,\rm m \ (\pm 0{,}01 \,\rm m) \ (\pm 0{,}2\%)</math> |
| − | :<math>t = 2 s (\pm 0,1 | + | :<math>t = 2 \,\rm s \ (\pm 0{,}1 \,\rm s) \ (\pm 5\%)</math> |
| − | :<math>v=\frac{s}{t}= 2,5 m/s | + | :<math>v=\frac{s}{t}= 2{,}5 \,\rm m/s \ (\pm 5{,}2\%)</math> |
Aus dem relativen Fehler ist es nun auch möglich wieder den absoluten Fehler zu berechnen. | Aus dem relativen Fehler ist es nun auch möglich wieder den absoluten Fehler zu berechnen. | ||
| Zeile 114: | Zeile 128: | ||
===Potenzen und Wurzeln=== | ===Potenzen und Wurzeln=== | ||
*Die relativen Fehler werden mit der Potenz gewichtet und addiert. | *Die relativen Fehler werden mit der Potenz gewichtet und addiert. | ||
| − | + | ;Beispiel: | |
| + | Bestimmung der kinetischen Energie eines Radfahrers. | ||
| + | :<math> | ||
| + | \begin{alignat}{2} | ||
| + | E_{kin} &= \frac{1}{2}\, m\, v^2 & \qquad (v \textrm{ in } \rm\frac{m}{s} )\\ | ||
| + | &= \frac{1}{2}\, m\, \frac{v^2}{3{,}6^2} & \qquad (v \textrm{ in } \rm\frac{km}{h} ) | ||
| + | \end{alignat} | ||
| + | </math> | ||
| + | :<math>m = 85,3\,\rm kg \ (\pm 0,1\,\rm kg) \ (\pm 0{,}12\%)</math> | ||
| + | :<math>v = 18\,\rm \frac{km}{h} \ (\pm 1 \,\rm\frac{km}{h}) \ (\pm 5{,}6\%) </math> | ||
| + | |||
| + | Der relative Messfehler der Geschwindigkeit wird nun doppelt gewichtet (mit zwei multipliziert): | ||
| + | :<math>E_{kin} = 1066{,}66\,\rm J \ (\pm 11{,}32\%)</math> | ||
| + | Um diese Messung zu verbessern, muss man vor allem die Geschwindigkeit genauer messen. | ||
| + | |||
| + | ;Beispiel: | ||
Bestimmung der Periodendauer eines Pendels. | Bestimmung der Periodendauer eines Pendels. | ||
| − | :<math>T = 2\ | + | :<math>T = 2\pi \, \frac{\sqrt{l}}{\sqrt{g}} = 2\pi \, \frac{l^{1/2}}{g^{1/2}}</math> |
| − | :<math>l = 0, | + | :<math>l = 0{,}6\,\rm m \ (\pm 0{,}1\%)</math> |
| − | :<math>g = 9,81 m/s^2 (\pm 0,01\%)</math> | + | :<math>g = 9{,}81 \,\rm m/s^2 \ (\pm 0{,}01\%)</math> |
Die relativen Messfehler werden nun mit 1/2 gewichtet (multipliziert) und addiert: | Die relativen Messfehler werden nun mit 1/2 gewichtet (multipliziert) und addiert: | ||
| − | :<math>T = 1,5539 s (\pm 0,055\%)</math> | + | :<math>T = 1{,}5539 s \ (\pm 0,055\%)</math> |
In diesem Fall ist also der Gesamtfehler kleiner als der größte Einzelfehler! | In diesem Fall ist also der Gesamtfehler kleiner als der größte Einzelfehler! | ||
| Zeile 134: | Zeile 163: | ||
==Links== | ==Links== | ||
| − | |||
*[http://www.jgiesen.de/Divers/Fehler/Fehlerrechnung.pdf Einfache Übersicht zu Fehlerrechnung und Ausgleichsgeraden.] (Von Jürgen Giesen) | *[http://www.jgiesen.de/Divers/Fehler/Fehlerrechnung.pdf Einfache Übersicht zu Fehlerrechnung und Ausgleichsgeraden.] (Von Jürgen Giesen) | ||
| + | *Video: [https://www.youtube.com/watch?v=Fegwu402YrM Vorlesung Physik II : Fehlerrechnung] (Professor Eckehard Müller, Fachbereich Mechatronik und Maschinenbau der Hochschule Bochum) | ||
*[http://www.idn.uni-bremen.de/cvpmm/content/fehlerrechnung/show.php?modul=2&ident=2021 Selbstlerneinheit Fehlerrechnung der Uni Bremen] (Von Dr. Stefan Käding und Dr. Elgar Fokkens) | *[http://www.idn.uni-bremen.de/cvpmm/content/fehlerrechnung/show.php?modul=2&ident=2021 Selbstlerneinheit Fehlerrechnung der Uni Bremen] (Von Dr. Stefan Käding und Dr. Elgar Fokkens) | ||
*[http://de.wikipedia.org/wiki/Physikalische_Gr%C3%B6%C3%9Fe Wikipedia: Physikalische Größen] | *[http://de.wikipedia.org/wiki/Physikalische_Gr%C3%B6%C3%9Fe Wikipedia: Physikalische Größen] | ||
Aktuelle Version vom 18. Januar 2022, 08:21 Uhr
(Kursstufe > Experimentell-induktives Vorgehen am Beispiel einer Schwingung)
Inhaltsverzeichnis
Wie lang ist das Zimmer?
Zunächst schätzen wir die Länge.
Zur Messung verwenden wir Zollstöcke. Mit einem Zollstock kann man die Länge bis auf einen halben Zentimeter genau ablesen.
Hier die Urliste der Daten:
Messergebnisse in Metern: 10,5 | 11,04 | 11,06 | 11,09 | 11,07 | 11,09 | 11,05 | 10,7 | 11,07 | 11,00 | 11,045 | 11,64 |
Manche Längen kommen häufiger vor als andere, hier die sortierte Liste:
10,5 | 10,7 | 11,00 | 11,04 | 11,045 | 11,05 | 11,06 | 11,64 | 11,07 | 11,07 | 11,09 | 11,09 |
Um die Häufigkeit eines Messwertes angeben zu können, teilt man den Messbereich in Klassen ein und gibt die Anzahl der Messwerte in dieser Klasse an:
Bereich | Häufigkeit 10,5 <= x < 11 | 2 11 <= x < 11,5 | 9 11,5 <= x < 12 | 1
Und das entsprechende Häufigkeitsdiagramm:
Auffällig ist, dass Werte abseits des Mittelwertes weniger häufig auftreten. Bei einer Messung treten also oft Werte um den Mittelwert auf. Es ist deshalb naheliegend, den Mittelwert der Messwerte als vermutliche Länge des Zimmers zu nehmen:
- [math]\bar l = 11{,}03 \,\rm m[/math]
Aber wie genau ist nun unsere Messung? Auf den Millimeter? Oder doch nur +/- einen Zentimeter?
Als Qualitätsmerkmal einer genauen Messung kann man die "Breite" der graphischen Darstellung annehmen. Je schmaler der Berg, desto besser die Messung.
Als Messfehler kann man nun eine Abweichung vom Mittelwert wählen, sodass bei einer erneuten Messung der Wert zu 50% oder zu 75% oder zu 90% oder zu 99% innerhalb des Abweichungsbereichs liegt. Die Wahrscheinlichkeit mit der ein Messwert innerhalb der Fehlerschranken liegt (das "Vertrauensniveau") kann man also wählen. Häufig liegt sie bei 67%.
(Bei einem Vertrauensniveau von 90% liegen 5% aller Werte unterhalb vom sogenannten Quantil [math]Q_{0.05}[/math] und 5% oberhalb vom Quantil [math]Q_{0.95}[/math] )
Systematische und zufällige Messfehler
- Jede Messung ermittelt nur einen ungenauen Wert einer Größe.
- Dabei enthaltene Messfehler teilt man in systematische und zufällige Fehler ein.
- Systematische Fehler entstehen z.B. durch einen falschen Versuchsaufbau. Sie verschieben die gemessenen Werte um einen festen Betrag. Sie sind schwer abzuschätzen oder zu korrigieren.
- Bei zufälligen Fehlern geht man davon aus, dass die Messwerte um den korrekten Wert schwanken. Zufällige Fehler werden durch Schwankungen der Messgröße, der Messgeräte, der Umwelt, durch den Beobachter etc. verursacht. Sie sind unvermeidbar, können aber abgeschätzt und durch Wiederholung verringert werden. Dazu verwendet man die Statistik.
- Graphische Veranschaulichung der Fehlertypen
Angabe von Messfehlern
- Als absolute Angabe mit Einheiten: [math]l=2\,\rm m \ (\pm 0,01\,\rm m) \qquad \qquad l = l_0 \pm \Delta l[/math]
- Als relative Angabe ohne Einheiten: [math]l=2\,\rm m \ (\pm 0,05)\ (\pm 5 \%) \qquad (\pm \frac{\Delta l}{l})[/math]
- Mit Hilfe von geltenden Ziffern, wobei nur die letzte Ziffer fehlerbehaftet ist: [math]l=2,000\,\rm m[/math]
Statistische Beurteilung von zufälligen Fehlern
- Dazu müssen eine möglichst große Anzahl von [math]N[/math] Messungen der gleichen Größe [math]x[/math] durchgeführt werden.
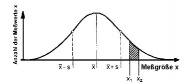
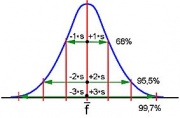
- Häufig kann man annehmen, dass der Messwert normalverteilt ist, die Häufigkeiten also der Gaußschen Glockenkurve entsprechen. (Das liegt daran, dass eine zufällige Größe, die von sehr vielen voneinander unabhängigen Einflüssen abhängt, normalverteilt ist. (Sogenannter "zentraler Grenzwertsatz"))
- Der Verlauf der Kurve und damit die Messwerte werden durch die Angabe des Mittelwerts ([math]\bar x[/math]) und der Standardabweichung ([math]s[/math] oder [math]\sigma[/math]) vollständig festgelegt. Der Mittelwert gibt den Ort des Maximums an, die Standardabweichung gibt den Abstand der Wendestellen von der Extremstelle an.
- [math]\bar x = \frac{\sum_{i=1}^N x_i}{N} \qquad \sigma = s = \sqrt{\frac{\sum_{i=1}^N (\bar x - x_i)^2}{N-1}}[/math]
- Die Standardabweichung der Messwerte gibt an, wie genau die Messungen waren. Kleine Abweichung = Genaue Messung. Man kann damit auch die Wahrscheinlichkeit angeben, dass ein Messwert innerhalb eines Bereichs liegt.
Maximale absolute Abweichung | Vertrauensniveau
s | 68% (ca. 2/3)
2 s | 95%
2,5 s | 99%
- Für das Gesamtergebnis ist aber nicht der einzelne Messwert, sondern der Mittelwert der N Messwerte interessant. Dies berücksichtigt dann auch die Tatsache, dass der Mittelwert immer weniger unsicher wird, je mehr Messungen durchgeführt werden!
- Für den Mittelwert gibt es auch eine Wahrscheinlichkeitsverteilung mit einer anderen Glockenkurve. Daraus ergibt sich die Standardabweichung des Mittelwertes [math]s_M[/math]. Sie ergibt eine Abschätzung für den Fehler des Mittelwertes und wird als Fehler der Messung angegeben.
- [math]s_M = \frac{s}{\sqrt{N}}[/math]
- Mit einer Wahrscheinlichkeit von 68% liegt also der Mittelwert der N Messungen im Bereich [math]\bar x \pm s_M[/math].
Beispielmessung einer Raumgröße
Die Länge eines Raumes wird von 12 Personen je einmal mit Hilfe eines Zollstocks gemessen.
Messergebnisse in Metern: 10,5 | 11,04 | 11,06 | 11,09 | 11,07 | 11,09 | 11,05 | 10,7 | 11,07 | 11,00 | 11,045 | 11,64 |
Mittelwert: 11,03 m Standardabweichung der Messwerte: 0,265 m Standardabweichung des Mittelwerts: 0,077 m
Endergebnis: l = 11,03 m (+- 7,7 cm)
Statistik-Auswertung mit dem GTR (TI-83)
Die Auswertung erfolgt in den folgenden Schritten:
- Eingabe der Daten mit STAT -> 1:Edit in die Listen L1, L2,...
- Berechnung und Anzeige von Werten mit STAT -> CALC -> 1: 1-Var Stats. Möchte man mehrere Listen bearbeiten, so gibt man z.B. 1-Var Stats L2 für die zweite Liste ein.
- Dabei ist Sx die Standardabweichung einer Stichprobe, die man benötigt, [math]\sigma x[/math] ist die Standardabweichung der Grundgesamtheit, die wir hier nicht benötigen.
- Berechnung der Standardabweichung des Mittelwertes ist im Rechenfenster möglich, indem man Sx durch die Wurzel der Anzahl der Messungen teilt.
- Will man Sx nicht abtippen, so kann man aus dem Variablenmenü VARS -> 5:Statistics -> 3: Sx wählen. Dort findet man auch Variablen für die Anzahl der Eingaben und den Mittelwert usw.
- Graphische Anzeigemöglichkeiten hat man zB. durch die Darstellung der Werte in einem Histogramm.
- In STAT PLOT -> 1:Plot1 stellt man die Anzeige auf On und wählt den Typ mit dem Balkendiagramm. Als Xlist wählt man L1.
- Mit GRAPH erhält man nun eine Darstellung der Häufigkeiten in einem Balkendiagramm.
- Eventuell muss man mit Hilfe von WINDOW oder ZOOM die Fenstergröße sinnvoll einstellen.
Fehlerfortpflanzung
- Häufig werden eine oder mehrere fehlerbehaftete Ergebnisse verwendet, um ein Gesamtergebnis zu berechnen, das natürlich auch fehlerbehaftet ist. Man spricht von Fehlerfortpflanzung.
Summen und Differenzen
- Die absoluten Fehler addieren sich.
- Beispiel
Es wird die Dicke eines Blatt Papiers zu [math]0{,}2\,\rm mm \ (\pm 0{,}01\,\rm mm)[/math] bestimmt. Für die Dicke von 50 Blättern ergibt sich: [math]10\,\rm mm \ (\pm 0{,}5\,\rm mm)[/math]
Produkte und Quotienten
- Die relativen Fehler addieren sich.
Beispiel: Zur Bestimmung der Geschwindigkeit wurde die Strecke und die Zeit gemessen:
- [math]s = 5\,\rm m \ (\pm 0{,}01 \,\rm m) \ (\pm 0{,}2\%)[/math]
- [math]t = 2 \,\rm s \ (\pm 0{,}1 \,\rm s) \ (\pm 5\%)[/math]
- [math]v=\frac{s}{t}= 2{,}5 \,\rm m/s \ (\pm 5{,}2\%)[/math]
Aus dem relativen Fehler ist es nun auch möglich wieder den absoluten Fehler zu berechnen.
Potenzen und Wurzeln
- Die relativen Fehler werden mit der Potenz gewichtet und addiert.
- Beispiel
Bestimmung der kinetischen Energie eines Radfahrers.
- [math] \begin{alignat}{2} E_{kin} &= \frac{1}{2}\, m\, v^2 & \qquad (v \textrm{ in } \rm\frac{m}{s} )\\ &= \frac{1}{2}\, m\, \frac{v^2}{3{,}6^2} & \qquad (v \textrm{ in } \rm\frac{km}{h} ) \end{alignat} [/math]
- [math]m = 85,3\,\rm kg \ (\pm 0,1\,\rm kg) \ (\pm 0{,}12\%)[/math]
- [math]v = 18\,\rm \frac{km}{h} \ (\pm 1 \,\rm\frac{km}{h}) \ (\pm 5{,}6\%) [/math]
Der relative Messfehler der Geschwindigkeit wird nun doppelt gewichtet (mit zwei multipliziert):
- [math]E_{kin} = 1066{,}66\,\rm J \ (\pm 11{,}32\%)[/math]
Um diese Messung zu verbessern, muss man vor allem die Geschwindigkeit genauer messen.
- Beispiel
Bestimmung der Periodendauer eines Pendels.
- [math]T = 2\pi \, \frac{\sqrt{l}}{\sqrt{g}} = 2\pi \, \frac{l^{1/2}}{g^{1/2}}[/math]
- [math]l = 0{,}6\,\rm m \ (\pm 0{,}1\%)[/math]
- [math]g = 9{,}81 \,\rm m/s^2 \ (\pm 0{,}01\%)[/math]
Die relativen Messfehler werden nun mit 1/2 gewichtet (multipliziert) und addiert:
- [math]T = 1{,}5539 s \ (\pm 0,055\%)[/math]
In diesem Fall ist also der Gesamtfehler kleiner als der größte Einzelfehler!
Literatur
- Walcher, Wilhelm; Praktikum der Physik - Stuttgart : Teubner, 1994. - 415 S. : ISBN 3-519-13038-6 (LB 85/205 = Lehrbuchsammlung II, Institutsviertel)
Links
- Einfache Übersicht zu Fehlerrechnung und Ausgleichsgeraden. (Von Jürgen Giesen)
- Video: Vorlesung Physik II : Fehlerrechnung (Professor Eckehard Müller, Fachbereich Mechatronik und Maschinenbau der Hochschule Bochum)
- Selbstlerneinheit Fehlerrechnung der Uni Bremen (Von Dr. Stefan Käding und Dr. Elgar Fokkens)
- Wikipedia: Physikalische Größen