*: Unterschied zwischen den Versionen

Aus Schulphysikwiki
Wechseln zu: Navigation, Suche
(→‎Leere Seite)
Zeile 5: Zeile 5:
 
|}
 
|}
 
__NOTOC__
 
__NOTOC__
 +
==Erklärung durch Überlagerung von Wellen als "Stehende Welle"==
 +
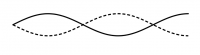
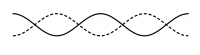
[[Datei:Standing waves1.gif|right|framed|Zwei Wellenzüge gleicher Wellenlänge und Amplitude überlagern sich.]][[Datei:Interferenz_Lautsprecher_Erklärung.jpg|thumb|Die stehende Welle zwischen zwei Quellen in 2D.]]
 +
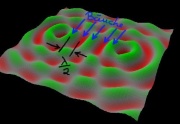
[[Datei:Interferenz_Lautsprecher_Erklärung_3d.jpg|thumb|und in 3D (Standbilder der [http://www.falstad.com/ripple/ Wellenwanne] von Paul Falstad.)]]
  
−
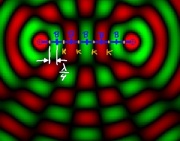
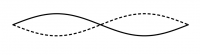
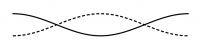
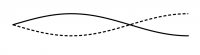
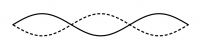
=Zeigermodell und Wellengleichung einer ebenen harmonischen Welle=
+
Überlagern sich zwei gegenläufige Wellen mit gleicher Wellenlänge und gleicher Amplitude, so ergibt sich in regelmäßigen Abständen von einem Viertel der Wellenlänge konstruktive und destruktive Interferenz. Dieses Phänomen hat man auch bei der [[Interferenz#Zwei-Quellen-Interferenz|Zwei-Quellen-Interferenz]] in dem Gebiet zwischen zwei Lautsprechern beobachten können.  
−
[[Bild:Welle_Phasenverschiebung.png|thumb|right|600px|Die Welle breitet sich nach rechts aus. Links sind die rotierenden Zeiger von A und B zu sehen. Die Schwingungen B, C,... hinken dem linken Nachbar jeweils um <math>2\pi / 8</math>, also 45° hinterher. (Aus den [http://www.geogebra.org/de/upload/files/dynamische_arbeitsblaetter/lwolf/wellen/welle2.html dynamischen Arbeitsblättern zur Wellenlehre].)]]
+
Die Überlagerung sieht aus wie eine "Stehende Welle" und heißt deswegen auch so. Die Stellen mit konstruktiver Interferenz heißen ''Bäuche'', die mit destruktiver Interferenz ''Knoten''. ([http://www.pk-applets.de/phy/interferenz/interferenz.html Animation])
  
−
Im Falle einer räumlich unbegrenzten, linearen harmonischen Welle kann man die Welle relativ einfach beschreiben. In einer solchen Welle sind alle Schwingungen harmonisch und die Welle breitet sich nur längs einer Raumrichtung aus. Kugelwellen, Kreiswellen oder Zylinderwellen sind also keine solchen Wellen, ebene Wellen schon. Außerdem werden räumlich begrenzte Wellenpakete ausgeschlossen.
+
Stehende Wellen sind aber keine Wellen mehr, sondern eine Schwingung durch die Formveränderung eines Körpers.
 +
Denn bei einer stehenden Welle wird überhaupt keine Energie oder Impuls transportiert. Beide Wellen haben die gleiche [[Energietransport_einer_Welle_(Intensität)|Intensität]], aber in gegenläufigen Richtungen.
  
−
Bei einer Welle regt eine Schwingung ihren Nachbarn in
+
Man kann die Eigenschwingungen von ausgedehnten Körpern aber sehr schön mit Hilfe von Wellen beschreiben.
−
Ausbreitungsrichtung zu erzwungenen Schwingungen an. Alle schwingen mit
+
An den Rändern des schwingenden Gegenstandes wird die Welle reflektiert. Je nach Art des Randes aber unterschiedlich, was man in [[Media:Welle_Reflektion_loses_festes_Ende.ogg|diesem Video]] sehen kann.
−
der gleichen Frequenz und der gleichen Amplitude. Die Schwinger hinken aber in
+
An einem offenen (losen) Ende wird ein Wellenberg als Wellenberg reflektiert. An einem geschlossenen (festen) Ende als Tal. Man kann auch sagen, dass die Welle bei einem festen Ende einen Phasensprung von <math>\pi</math> macht.
−
Ausbreitungsrichtung der ursprünglichen Schwingung hinterher, wodurch
+
 
−
sich eine Phasenverschiebung ergibt. Im Abstand einer halben
+
Überlagert sich die einlaufende Welle mit der reflektierten, so entsteht eine stehende Welle. Das ist in dieser [http://www.walter-fendt.de/ph14d/stwellerefl.htm Animation] nachzuvollziehen.
−
Wellenlänge beträgt sie gerade <math>\pi</math>, so dass die Schwingungen gegenphasig sind, bei einer ganzen Wellenlänge sind es <math>2 \ \pi</math>, womit die Schwingungen wieder in Phase sind.  
+
 
−
<br style="clear: both" />
+
 
 +
 
 +
<gallery widths=200px heights=70px  perrow=3 >
 +
Bild:Stehende_Welle_gg0.png|<math>\text{ } \quad \lambda_0= \frac{4}{2} \, l \qquad f_0=\frac{2}{4}\, \frac{c}{l} </math>
 +
Bild:Stehende_Welle_oo0.png|<math>\text{ } \quad \lambda_0= \frac{4}{2} \, l \qquad f_0=\frac{2}{4}\, \frac{c}{l} </math>
 +
Bild:Stehende_Welle_go0.png|<math>\text{ } \quad \lambda_0= \frac{4}{1} \, l \qquad f_0=\frac{1}{4}\, \frac{c}{l} </math>
 +
Bild:Stehende_Welle_gg1.png|<math>\text{ } \quad \lambda_1= \frac{4}{4} \, l \qquad f_1=\frac{4}{4}\, \frac{c}{l} </math>
 +
Bild:Stehende_Welle_oo1.png|<math>\text{ } \quad \lambda_1= \frac{4}{4} \, l \qquad f_1=\frac{4}{4}\, \frac{c}{l} </math>
 +
Bild:Stehende_Welle_go1.png|<math>\text{ } \quad \lambda_1= \frac{4}{3} \, l \qquad f_1=\frac{3}{4}\, \frac{c}{l} </math>
 +
Bild:Stehende_Welle_gg2.png|<math>\text{ } \quad \lambda_2= \frac{4}{6} \, l \qquad f_2=\frac{6}{4}\, \frac{c}{l} </math>
 +
Bild:Stehende_Welle_oo2.png|<math>\text{ } \quad \lambda_2= \frac{4}{6} \, l \qquad f_2=\frac{6}{4}\, \frac{c}{l} </math>
 +
Bild:Stehende_Welle_go2.png|<math>\text{ } \quad \lambda_2= \frac{4}{5} \, l \qquad f_2=\frac{5}{4}\, \frac{c}{l} </math>
 +
Bild:Stehende_Welle_gg3.png|<math>\text{ } \quad \lambda_3= \frac{4}{8} \, l \qquad f_3=\frac{8}{4}\, \frac{c}{l} </math>
 +
Bild:Stehende_Welle_oo3.png|<math>\text{ } \quad \lambda_3= \frac{4}{8} \, l \qquad f_3=\frac{8}{4}\, \frac{c}{l} </math>
 +
Bild:Stehende_Welle_go3.png|<math>\text{ } \quad \lambda_3= \frac{4}{7} \, l \qquad f_3=\frac{7}{4}\, \frac{c}{l} </math>
 +
</gallery>
 +
 
 +
 
 +
Die Eigenfrequenzen unterscheiden sich also je nachdem, ob beide Randbedingungen gleich (offen-offen und geschlossen-geschlossen) oder unterschiedlich sind.
 +
 
 +
{|class="wikitable"
 +
|style="border-style: solid; border-width: 4px "|
 +
Bei symmetrischen Randbedingen sind alle Vielfache der Grundfrequenz Eigenfrequenzen.
 +
:<math> f_n=\frac{2 \,(n+1)}{4}\, \frac{c}{l} \qquad f_n=(n+1)\, f_0 </math>  
 +
 
 +
Bei unsymmetrischen Randbedingen sind nur ungeradzahlige Vielfache der Grundfrequenz Eigenfrequenzen.
 +
:<math> f_n=\frac{2 \,(n+1)-1}{4}\, \frac{c}{l} \qquad f_n=(2\,(n+1)-1)\, f_0 </math>
 +
|}

Version vom 2. Februar 2022, 19:21 Uhr

Leere Seite

Erklärung durch Überlagerung von Wellen als "Stehende Welle"

Zwei Wellenzüge gleicher Wellenlänge und Amplitude überlagern sich.
Die stehende Welle zwischen zwei Quellen in 2D.
und in 3D (Standbilder der Wellenwanne von Paul Falstad.)

Überlagern sich zwei gegenläufige Wellen mit gleicher Wellenlänge und gleicher Amplitude, so ergibt sich in regelmäßigen Abständen von einem Viertel der Wellenlänge konstruktive und destruktive Interferenz. Dieses Phänomen hat man auch bei der Zwei-Quellen-Interferenz in dem Gebiet zwischen zwei Lautsprechern beobachten können. Die Überlagerung sieht aus wie eine "Stehende Welle" und heißt deswegen auch so. Die Stellen mit konstruktiver Interferenz heißen Bäuche, die mit destruktiver Interferenz Knoten. (Animation)

Stehende Wellen sind aber keine Wellen mehr, sondern eine Schwingung durch die Formveränderung eines Körpers. Denn bei einer stehenden Welle wird überhaupt keine Energie oder Impuls transportiert. Beide Wellen haben die gleiche Intensität, aber in gegenläufigen Richtungen.

Man kann die Eigenschwingungen von ausgedehnten Körpern aber sehr schön mit Hilfe von Wellen beschreiben. An den Rändern des schwingenden Gegenstandes wird die Welle reflektiert. Je nach Art des Randes aber unterschiedlich, was man in diesem Video sehen kann. An einem offenen (losen) Ende wird ein Wellenberg als Wellenberg reflektiert. An einem geschlossenen (festen) Ende als Tal. Man kann auch sagen, dass die Welle bei einem festen Ende einen Phasensprung von [math]\pi[/math] macht.

Überlagert sich die einlaufende Welle mit der reflektierten, so entsteht eine stehende Welle. Das ist in dieser Animation nachzuvollziehen.


  • [math]\text{ } \quad \lambda_0= \frac{4}{2} \, l \qquad f_0=\frac{2}{4}\, \frac{c}{l} [/math]

  • [math]\text{ } \quad \lambda_0= \frac{4}{2} \, l \qquad f_0=\frac{2}{4}\, \frac{c}{l} [/math]

  • [math]\text{ } \quad \lambda_0= \frac{4}{1} \, l \qquad f_0=\frac{1}{4}\, \frac{c}{l} [/math]

  • [math]\text{ } \quad \lambda_1= \frac{4}{4} \, l \qquad f_1=\frac{4}{4}\, \frac{c}{l} [/math]

  • [math]\text{ } \quad \lambda_1= \frac{4}{4} \, l \qquad f_1=\frac{4}{4}\, \frac{c}{l} [/math]

  • [math]\text{ } \quad \lambda_1= \frac{4}{3} \, l \qquad f_1=\frac{3}{4}\, \frac{c}{l} [/math]

  • [math]\text{ } \quad \lambda_2= \frac{4}{6} \, l \qquad f_2=\frac{6}{4}\, \frac{c}{l} [/math]

  • [math]\text{ } \quad \lambda_2= \frac{4}{6} \, l \qquad f_2=\frac{6}{4}\, \frac{c}{l} [/math]

  • [math]\text{ } \quad \lambda_2= \frac{4}{5} \, l \qquad f_2=\frac{5}{4}\, \frac{c}{l} [/math]

  • [math]\text{ } \quad \lambda_3= \frac{4}{8} \, l \qquad f_3=\frac{8}{4}\, \frac{c}{l} [/math]

  • [math]\text{ } \quad \lambda_3= \frac{4}{8} \, l \qquad f_3=\frac{8}{4}\, \frac{c}{l} [/math]

  • [math]\text{ } \quad \lambda_3= \frac{4}{7} \, l \qquad f_3=\frac{7}{4}\, \frac{c}{l} [/math]


Die Eigenfrequenzen unterscheiden sich also je nachdem, ob beide Randbedingungen gleich (offen-offen und geschlossen-geschlossen) oder unterschiedlich sind.

Bei symmetrischen Randbedingen sind alle Vielfache der Grundfrequenz Eigenfrequenzen.

[math] f_n=\frac{2 \,(n+1)}{4}\, \frac{c}{l} \qquad f_n=(n+1)\, f_0 [/math]

Bei unsymmetrischen Randbedingen sind nur ungeradzahlige Vielfache der Grundfrequenz Eigenfrequenzen.

[math] f_n=\frac{2 \,(n+1)-1}{4}\, \frac{c}{l} \qquad f_n=(2\,(n+1)-1)\, f_0 [/math]
Von „http://schulphysikwiki.de/index.php?title=*&oldid=16227“