Lösungen der Aufgaben zum Licht als Teilchen: Unterschied zwischen den Versionen
(→Sonnenbrand) |
(→Compton-Effekt) |
||
| (15 dazwischenliegende Versionen des gleichen Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | ([[Inhalt_Kursstufe|'''Kursstufe''']] > [[Inhalt_Kursstufe#Licht als Teilchen|'''Licht als Teilchen''']]) | ||
| + | |||
====Energie von Photonen==== | ====Energie von Photonen==== | ||
Lichtart Wellenlänge Frequenz mit <math>c= \, \lambda \, f</math> Energie mit <math>E=h\, f</math> und in eV mit <math>E= \, e\, U</math> | Lichtart Wellenlänge Frequenz mit <math>c= \, \lambda \, f</math> Energie mit <math>E=h\, f</math> und in eV mit <math>E= \, e\, U</math> | ||
| Zeile 23: | Zeile 25: | ||
====Photoeffekt: Geschwindigkeit eines Elektrons==== | ====Photoeffekt: Geschwindigkeit eines Elektrons==== | ||
| − | + | Die Energie des Photons wird dazu gebraucht, um das Elektron aus dem Atom auszulösen. Die restliche Energie erhält das Elektron als kinetische Energie: | |
| + | :<math>E_{Ph}=E_{Aus}+E_{kin}</math> | ||
| + | Die Ionisierungsenergie beträgt in Joule: | ||
| + | :<math>E_{Aus}=4,34\cdot 1,6\cdot 10^{-19}\, \rm J = 6,9\cdot 10^{-19}\, \rm J</math> | ||
| + | Die Energie des Photons mit <math>f=\frac{c}{\lambda}</math>: | ||
| + | :<math>E_{Ph}=h\, f = \frac{h\, c}{\lambda}= 9,9\cdot 10^{-19}\, \rm J</math> | ||
| + | Nun kann man über die kinetische Energie die Geschwindigkeit berechnen: | ||
| + | :<math>E_{kin}=\frac{1}{2}\, m\, v^2 =9,9\cdot 10^{-19}\, \rm J - 6,9\cdot 10^{-19}\, \rm J = 3,0\cdot 10^{-19}\, \rm J</math> | ||
| + | :<math>v=\sqrt{\frac{2 \cdot E_{kin}}{m}} = 812000 \, \rm \frac{m}{s}</math> | ||
| + | Das sind ca. 3% der Lichtgeschwindigkeit. | ||
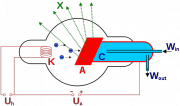
====Röntgenröhre==== | ====Röntgenröhre==== | ||
[[Datei:Roentgen-Roehre.png|thumb|left]] | [[Datei:Roentgen-Roehre.png|thumb|left]] | ||
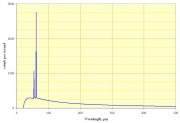
[[Datei:Bremsstrahlung Rh 60kV.jpg|thumb|right|Intensität in Abhängigkeit von der Wellenlänge. Anodenmaterial: Rhodium]] | [[Datei:Bremsstrahlung Rh 60kV.jpg|thumb|right|Intensität in Abhängigkeit von der Wellenlänge. Anodenmaterial: Rhodium]] | ||
| − | |||
| − | + | Die kinetische Energie eines Elektrons wird von der Beschleunigungsspannung festgelegt. Wird ein Elektron vollständig abgebremst, kann es seine gesamte kinetische Energie an das entstehende Lichtteilchen abgeben. Lichteilchen, die mehr Energie enthalten, können also nicht entstehen. Demnach hat das ausgesandte Röntgenlicht eine maximale Frequenz und somit eine minimale Wellenlänge. | |
| − | + | Die kleinste Wellenlänge der ausgesandten Strahlung beträgt ungefähr <math>20\, \rm pm=20\cdot 10^{-12} \rm m</math>. | |
| − | + | ||
| − | + | ||
| + | Demnach beträgt die maximale Energie der Photonen: | ||
| + | :<math>E=h \, f = \frac{h\, c}{\lambda}= \frac{6{,}6\cdot 10^{-34} \rm \frac{J}{Hz}\ 3\cdot10^8\, \frac{m}{s}}{20\cdot10^{-12} \rm m}=9{,}9\cdot 10^{-15} \rm J = 61900 \, \rm eV</math> | ||
| + | Logischerweise betrug die Beschleunigungsspannung also <math>61900 \, \rm V</math>! | ||
====Bestimmung von h mit der Gegenfeldmethode==== | ====Bestimmung von h mit der Gegenfeldmethode==== | ||
| Zeile 54: | Zeile 65: | ||
====Masse und Impuls eines Photons==== | ====Masse und Impuls eines Photons==== | ||
| − | + | Für die Wellenlänge und den Impuls eines Photons gilt: | |
| + | :<math>p=m\, c</math> | ||
| + | :<math>\lambda=\frac{h}{p}</math> | ||
| + | Also folgt daraus für die Photonenmasse: | ||
| + | :<math>m=\frac{h}{\lambda \, c}</math> | ||
| + | Lichtart Wellenlänge Masse Impuls | ||
| + | Röntgenstrahlung 0,01 nm 2 10^-31 kg 7 10^-23 Hy | ||
| + | blaues Licht 450 nm 5 10^-36 kg 1 10^-27 Hy | ||
| + | Radiowellen 3 m (UKW) 1 10^-43 kg 2 10^-34 Hy | ||
| + | |||
| + | Die Masse eines Photons der Röntgenstrahlung liegt also im Bereich der Elektronenmasse. Bei langwelligerer Strahlung ist die Masse extrem klein. | ||
====Licht als Antrieb==== | ====Licht als Antrieb==== | ||
| Zeile 62: | Zeile 83: | ||
Die Kraft, die auf die Lampe wirkt, kann man, wie bei einer Rakete, über die Impulsänderung berechnen: <math>F=\frac{p}{t}</math>. | Die Kraft, die auf die Lampe wirkt, kann man, wie bei einer Rakete, über die Impulsänderung berechnen: <math>F=\frac{p}{t}</math>. | ||
*Wieviel Impuls erhält ein Photon, dass von der Lampe ausgesendet wird? | *Wieviel Impuls erhält ein Photon, dass von der Lampe ausgesendet wird? | ||
| + | |||
| + | Der Einfachheit halber betrachtet man die "roten Photonen" (650 nm), die auch in der Mehrzahl von der Lampe ausgesendet werden. | ||
| + | Ihr Impuls beträgt: | ||
| + | :<math>p=\frac{h}{\lambda}= \frac{6{,6}\cdot10^{-34}\rm \frac{J}{Hz}}{650\cdot10^{-9}\rm m}= 1{,0}\cdot10^{-27}\rm Hy</math> | ||
| + | |||
| + | |||
*Berechnen Sie die Anzahl der Photonen pro Sekunde bei einer idealen 3Watt-Lampe und daraus die auf die Lampe wirkende Kraft. | *Berechnen Sie die Anzahl der Photonen pro Sekunde bei einer idealen 3Watt-Lampe und daraus die auf die Lampe wirkende Kraft. | ||
| + | Die Energie eines Photons beträgt: | ||
| + | :<math>E=h\, f = \frac{h\, c}{\lambda}= \frac{6{,6}\cdot10^{-34}\rm \frac{J}{Hz}\, 3\cdot 10^8 \rm \frac{m}{s}}{650\cdot10^{-9}\rm m}= 3{,0}\cdot10^{-19}\rm J </math> | ||
| + | Die Lampe strahlt in der Sekunde 3 Joule Energie ab, das entspricht daher <math>10^{19}</math> Photonen pro Sekunde: | ||
| + | :<math>E_{Lampe}=3\, \rm J = 10^{19} \cdot 3{,0}\cdot10^{-19}\rm J </math> | ||
| − | Bei einem Sonnensegel eines Satelliten versucht man das von der Sonne ausgesendete Licht möglichst in die Gegenrichtung zu reflektieren. Wegen der Impulserhaltung erhält dabei das Segel von jedem Photon den doppelten Impulsbetrag. | + | Der Impuls, den alle Photonen pro Sekunde erhalten, also die Kraft beträgt daher: |
| − | + | :<math>F=\frac{p}{t}= 10^{19}\cdot 1{,0}\cdot10^{-27}\rm N = 1\cdot10^{-7}\rm N</math> | |
| + | |||
| + | Das ist nicht gerade viel, aber immerhin... | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | *Bei einem Sonnensegel eines Satelliten versucht man das von der Sonne ausgesendete Licht möglichst in die Gegenrichtung zu reflektieren. Wegen der Impulserhaltung erhält dabei das Segel von jedem Photon den doppelten Impulsbetrag. | ||
| + | |||
| + | :Berechnen Sie die maximale Kraft auf ein Sonnensegel mit einer Fläche von 5m^2. Dabei befindet sich das Segel in Erdnähe. Dort beträgt die Strahlungsleistung ca. 1350Watt pro m^2. (Auf der Erde kommt ca. die Hälfte davon noch an!) | ||
| + | |||
| + | Man kann von der 3Watt-Lampe der vorherigen Aufgabe ausgehen. Pro Watt beträgt die Kraft auf die Photonen aus der Ruhe im Mittel: | ||
| + | :<math>\frac{F}{P}=\frac{1\cdot10^{-7}\rm N}{3 W}= 3{,}3\cdot10^{-8}\rm \frac{N}{W}</math> | ||
| + | Durch die Reflektion ist die Impulsänderung, also auch die Kraft doppelt sogroß. | ||
| + | |||
| + | Jetzt muss man nur noch ausrechnen, wieviel "Watt vom Sonnensegel aufgefangen" wird: | ||
| + | :<math>P_{Segel}=5\cdot1350 \, \rm W = 6750\, \rm W</math> | ||
| + | |||
| + | Also beträgt die Kraft auf den Satelliten: | ||
| + | :<math>F_{Satellit}=2\cdot 6750 \, \rm W \cdot 3{,}3\cdot10^{-8}\rm \frac{N}{W}= 4{,}5\cdot10^{-4}\rm N</math> | ||
| + | Nun ja, immerhin schon fast ein milliNewton. | ||
| + | |||
| + | Einen Satellit, mit der Masse von 100kg könnte man so innerhalb eines Jahres beschleunigen: | ||
| + | :<math>p=m\, v = F\, t</math> | ||
| + | :<math>v=\frac{F\, t}{m}= \frac{4{,}5\cdot10^{-4}\rm N\, 365\cdot 24\cdot 60\cdot 60 \, \rm s}{100\, \rm kg}= 140 \, \rm \frac{m}{s}=500\, \rm \frac{km}{h}</math> | ||
| + | Wenn man viel Zeit hat, dann kann man das Sonnensegel also tatsächlich nutzen. | ||
====Compton-Effekt==== | ====Compton-Effekt==== | ||
Trifft eine em-Welle auf ein ruhendes Elektron, so wird die Welle in alle Richtungen gestreut. Man kann beobachten, dass die Wellenlänge der gestreuten Welle mit dem Ablenkungswinkel zunimmt. | Trifft eine em-Welle auf ein ruhendes Elektron, so wird die Welle in alle Richtungen gestreut. Man kann beobachten, dass die Wellenlänge der gestreuten Welle mit dem Ablenkungswinkel zunimmt. | ||
*Erklären sie das Phänomen mit dem Teilchenmodell. Machen Sie eine Zeichnung der Impulsvektoren von Photon und Elektron für einen Ablenkungswinkel von 90° und von 180° (Rückwärtsstreuung). | *Erklären sie das Phänomen mit dem Teilchenmodell. Machen Sie eine Zeichnung der Impulsvektoren von Photon und Elektron für einen Ablenkungswinkel von 90° und von 180° (Rückwärtsstreuung). | ||
| + | |||
| + | Im Teilchenmodell des Lichts hängt die Wellenlänge mit dem Impuls des Photons zusammen: | ||
| + | :<math>\lambda=\frac{h}{p}</math> | ||
| + | Je größer der Impuls, desto kleiner die Wellenlänge. | ||
| + | |||
| + | Den Zusammenstoß von Photon und Elektron kann man sich vereinfacht als den Zusammenstoß zweier Kugeln vorstellen. Dabei verändert sich der Impuls des Photons in Richtung und Betrag. Je größer der Ablenkungswinkel ist, desto mehr nimmt der Impulsbetrag des gestreuten Photons ab. Das kann man gut durch die Vektoraddition der Impulse sehen. | ||
| + | |||
| + | |||
| + | Bei dieser Animation wird die Impulsänderung beim Stoß veranschaulicht. Das Elektron ruht vor dem Zusammenstoß. | ||
| + | |||
| + | Man kann die Masse des Photons als Anteil der Elektronenmasse einstellen. Zu Beginn beträgt sie 5% der Elektronenmasse. | ||
| + | |||
| + | Mit dem grünen Schieberegler kann man den Auftreffpunkt des Photons auf das Elektron verschieben. | ||
| + | |||
| + | {{#widget:Iframe | ||
| + | |url=https://www.geogebra.org/material/iframe/id/veJsvDRB/width/800/height/530/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/false/rc/false/ld/false/sdz/false/ctl/false | ||
| + | |width=600 | ||
| + | |height=400 | ||
| + | |border=0 | ||
| + | }} | ||
| + | |||
| + | (Zur [https://www.geogebra.org/material/show/id/veJsvDRB Datei] und zum [https://www.geogebra.org/download?lang=de Programm]) | ||
| + | |||
*Warum ist der Effekt für Photonen mit größerer Wellenlänge, also kleinem Impuls zu vernachlässigen? Vergleichen Sie dazu den Zusammenstoß einer leichten und einer schweren Kugel mit einer ruhenden bei diesem [http://www.pk-applets.de/phy/stoss/stoss.html Applet]. | *Warum ist der Effekt für Photonen mit größerer Wellenlänge, also kleinem Impuls zu vernachlässigen? Vergleichen Sie dazu den Zusammenstoß einer leichten und einer schweren Kugel mit einer ruhenden bei diesem [http://www.pk-applets.de/phy/stoss/stoss.html Applet]. | ||
| + | |||
| + | Photonen mit großer Wellenlänge haben eine im Vergleich zum Elektron kleine Masse. Daher werden sie beim Zusammenstoß mit dem Elektron mit fast dem gleichen Impulsbetrag reflektiert und die Wellenlänge ändert sich fast nicht. (So ähnlich wie ein Ball an einer Wand.) | ||
| + | |||
| + | Photonen von Röntgenlicht (ab 1nm) und noch kurzwelligerer Strahlung haben eine Masse von 2% und mehr der Elektronenmasse. Beim Zusammenstoß mit einem Elektron verändert sich der Impulsbetrag und damit die Wellenlänge merklich. | ||
Aktuelle Version vom 9. Februar 2023, 15:56 Uhr
(Kursstufe > Licht als Teilchen)
Inhaltsverzeichnis
Energie von Photonen
Lichtart Wellenlänge Frequenz mit [math]c= \, \lambda \, f[/math] Energie mit [math]E=h\, f[/math] und in eV mit [math]E= \, e\, U[/math] UV-Licht 200 nm 1,5 10^15 Hz 9,9 10^-19 J 6,2 eV blaue 450 nm 6,7 10^14 Hz 4,4 10^-19 J 2,8 eV rot 650 nm 4,6 10^14 Hz 3 10^-19 J 1,9 eV Handywellen 15 cm (E-Netz) 2 10^ 9 Hz 1,3 10^-24 J 8,3 10^-6 eV Radiowellen 3 m (UKW) 1 10^ 8 Hz 6,6 10^-26 J 4,1 10^-7 eV
Ionisierungsenergie von Ammoniak
Ionisierungsenergie in Joule: [math]E= 10{,}16 \cdot 1{,}6\cdot 10^{-19}\rm J = 1{,}626 \cdot 10^{-18} \rm J[/math]
Mit [math]c=\lambda \, f[/math] und [math]E = h \, f[/math] folgt:
- [math]\lambda = \frac{h\, c}{E} = 1{,}22\cdot 10^{-7} \rm m = 122 \, \rm nm[/math]
Das ist die Wellenlänge von kurzwelligem UV-Licht (UV-C-Strahlen).
Sonnenbrand
Sonnenbrand bekommt man durch Ionisation der Moleküle des Gewebes, also durch den Photoeffekt.
Aus Sicht der Wellentheorie spielt dabei die Frequenz der em-Welle keine Rolle, da bei allen Frequenzen durch eine große Amplitude genügend Energie transportiert werden kann.
Aus Sicht der Teilchentheorie ist es verständlich, daß ein Photon erst ab einer gewissen Energiemenge ein Elektron aus dem Atom herauslösen kann. Die Energiemenge eines Photons hängt aber von der Frequenz ab [math]E=h\, f[/math]. Die Lichtteilchen von sichtbarem Licht haben zu wenig Energie, erst die Photonen von UV-Licht sind energiereich genug.
Photoeffekt: Geschwindigkeit eines Elektrons
Die Energie des Photons wird dazu gebraucht, um das Elektron aus dem Atom auszulösen. Die restliche Energie erhält das Elektron als kinetische Energie:
- [math]E_{Ph}=E_{Aus}+E_{kin}[/math]
Die Ionisierungsenergie beträgt in Joule:
- [math]E_{Aus}=4,34\cdot 1,6\cdot 10^{-19}\, \rm J = 6,9\cdot 10^{-19}\, \rm J[/math]
Die Energie des Photons mit [math]f=\frac{c}{\lambda}[/math]:
- [math]E_{Ph}=h\, f = \frac{h\, c}{\lambda}= 9,9\cdot 10^{-19}\, \rm J[/math]
Nun kann man über die kinetische Energie die Geschwindigkeit berechnen:
- [math]E_{kin}=\frac{1}{2}\, m\, v^2 =9,9\cdot 10^{-19}\, \rm J - 6,9\cdot 10^{-19}\, \rm J = 3,0\cdot 10^{-19}\, \rm J[/math]
- [math]v=\sqrt{\frac{2 \cdot E_{kin}}{m}} = 812000 \, \rm \frac{m}{s}[/math]
Das sind ca. 3% der Lichtgeschwindigkeit.
Röntgenröhre
Die kinetische Energie eines Elektrons wird von der Beschleunigungsspannung festgelegt. Wird ein Elektron vollständig abgebremst, kann es seine gesamte kinetische Energie an das entstehende Lichtteilchen abgeben. Lichteilchen, die mehr Energie enthalten, können also nicht entstehen. Demnach hat das ausgesandte Röntgenlicht eine maximale Frequenz und somit eine minimale Wellenlänge.
Die kleinste Wellenlänge der ausgesandten Strahlung beträgt ungefähr [math]20\, \rm pm=20\cdot 10^{-12} \rm m[/math].
Demnach beträgt die maximale Energie der Photonen:
- [math]E=h \, f = \frac{h\, c}{\lambda}= \frac{6{,}6\cdot 10^{-34} \rm \frac{J}{Hz}\ 3\cdot10^8\, \frac{m}{s}}{20\cdot10^{-12} \rm m}=9{,}9\cdot 10^{-15} \rm J = 61900 \, \rm eV[/math]
Logischerweise betrug die Beschleunigungsspannung also [math]61900 \, \rm V[/math]!
Bestimmung von h mit der Gegenfeldmethode
Den Versuchsaufbau kann man sich hier noch einmal anschauen. Als Anodenmaterial wird Cäsium verwendet. Folgende Messwerte sind das Ergebnis der Messung:
Wellenlänge (nm)| Gegenspannung (V)| kin. Energie in J |
411 | 0,81 | |
447 | 0,62 | |
492 | 0,41 | |
534 | 0,28 | |
590 | - | |
- Ergänzen Sie die kinetische Energie des ausgelösten Elektrons und tragen Sie die kinetische Energie über die Frequenz in einem Diagramm auf.
- Bestimmen Sie aus dem Diagramm das Plancksche Wirkungsquantum und die Auslösearbeit für Cäsium.
Masse und Impuls eines Photons
Für die Wellenlänge und den Impuls eines Photons gilt:
- [math]p=m\, c[/math]
- [math]\lambda=\frac{h}{p}[/math]
Also folgt daraus für die Photonenmasse:
- [math]m=\frac{h}{\lambda \, c}[/math]
Lichtart Wellenlänge Masse Impuls Röntgenstrahlung 0,01 nm 2 10^-31 kg 7 10^-23 Hy blaues Licht 450 nm 5 10^-36 kg 1 10^-27 Hy Radiowellen 3 m (UKW) 1 10^-43 kg 2 10^-34 Hy
Die Masse eines Photons der Röntgenstrahlung liegt also im Bereich der Elektronenmasse. Bei langwelligerer Strahlung ist die Masse extrem klein.
Licht als Antrieb
Kann man das Licht einer Taschenlampe als Antrieb im All nutzen?
Die Kraft, die auf die Lampe wirkt, kann man, wie bei einer Rakete, über die Impulsänderung berechnen: [math]F=\frac{p}{t}[/math].
- Wieviel Impuls erhält ein Photon, dass von der Lampe ausgesendet wird?
Der Einfachheit halber betrachtet man die "roten Photonen" (650 nm), die auch in der Mehrzahl von der Lampe ausgesendet werden. Ihr Impuls beträgt:
- [math]p=\frac{h}{\lambda}= \frac{6{,6}\cdot10^{-34}\rm \frac{J}{Hz}}{650\cdot10^{-9}\rm m}= 1{,0}\cdot10^{-27}\rm Hy[/math]
- Berechnen Sie die Anzahl der Photonen pro Sekunde bei einer idealen 3Watt-Lampe und daraus die auf die Lampe wirkende Kraft.
Die Energie eines Photons beträgt:
- [math]E=h\, f = \frac{h\, c}{\lambda}= \frac{6{,6}\cdot10^{-34}\rm \frac{J}{Hz}\, 3\cdot 10^8 \rm \frac{m}{s}}{650\cdot10^{-9}\rm m}= 3{,0}\cdot10^{-19}\rm J [/math]
Die Lampe strahlt in der Sekunde 3 Joule Energie ab, das entspricht daher [math]10^{19}[/math] Photonen pro Sekunde:
- [math]E_{Lampe}=3\, \rm J = 10^{19} \cdot 3{,0}\cdot10^{-19}\rm J [/math]
Der Impuls, den alle Photonen pro Sekunde erhalten, also die Kraft beträgt daher:
- [math]F=\frac{p}{t}= 10^{19}\cdot 1{,0}\cdot10^{-27}\rm N = 1\cdot10^{-7}\rm N[/math]
Das ist nicht gerade viel, aber immerhin...
- Bei einem Sonnensegel eines Satelliten versucht man das von der Sonne ausgesendete Licht möglichst in die Gegenrichtung zu reflektieren. Wegen der Impulserhaltung erhält dabei das Segel von jedem Photon den doppelten Impulsbetrag.
- Berechnen Sie die maximale Kraft auf ein Sonnensegel mit einer Fläche von 5m^2. Dabei befindet sich das Segel in Erdnähe. Dort beträgt die Strahlungsleistung ca. 1350Watt pro m^2. (Auf der Erde kommt ca. die Hälfte davon noch an!)
Man kann von der 3Watt-Lampe der vorherigen Aufgabe ausgehen. Pro Watt beträgt die Kraft auf die Photonen aus der Ruhe im Mittel:
- [math]\frac{F}{P}=\frac{1\cdot10^{-7}\rm N}{3 W}= 3{,}3\cdot10^{-8}\rm \frac{N}{W}[/math]
Durch die Reflektion ist die Impulsänderung, also auch die Kraft doppelt sogroß.
Jetzt muss man nur noch ausrechnen, wieviel "Watt vom Sonnensegel aufgefangen" wird:
- [math]P_{Segel}=5\cdot1350 \, \rm W = 6750\, \rm W[/math]
Also beträgt die Kraft auf den Satelliten:
- [math]F_{Satellit}=2\cdot 6750 \, \rm W \cdot 3{,}3\cdot10^{-8}\rm \frac{N}{W}= 4{,}5\cdot10^{-4}\rm N[/math]
Nun ja, immerhin schon fast ein milliNewton.
Einen Satellit, mit der Masse von 100kg könnte man so innerhalb eines Jahres beschleunigen:
- [math]p=m\, v = F\, t[/math]
- [math]v=\frac{F\, t}{m}= \frac{4{,}5\cdot10^{-4}\rm N\, 365\cdot 24\cdot 60\cdot 60 \, \rm s}{100\, \rm kg}= 140 \, \rm \frac{m}{s}=500\, \rm \frac{km}{h}[/math]
Wenn man viel Zeit hat, dann kann man das Sonnensegel also tatsächlich nutzen.
Compton-Effekt
Trifft eine em-Welle auf ein ruhendes Elektron, so wird die Welle in alle Richtungen gestreut. Man kann beobachten, dass die Wellenlänge der gestreuten Welle mit dem Ablenkungswinkel zunimmt.
- Erklären sie das Phänomen mit dem Teilchenmodell. Machen Sie eine Zeichnung der Impulsvektoren von Photon und Elektron für einen Ablenkungswinkel von 90° und von 180° (Rückwärtsstreuung).
Im Teilchenmodell des Lichts hängt die Wellenlänge mit dem Impuls des Photons zusammen:
- [math]\lambda=\frac{h}{p}[/math]
Je größer der Impuls, desto kleiner die Wellenlänge.
Den Zusammenstoß von Photon und Elektron kann man sich vereinfacht als den Zusammenstoß zweier Kugeln vorstellen. Dabei verändert sich der Impuls des Photons in Richtung und Betrag. Je größer der Ablenkungswinkel ist, desto mehr nimmt der Impulsbetrag des gestreuten Photons ab. Das kann man gut durch die Vektoraddition der Impulse sehen.
Bei dieser Animation wird die Impulsänderung beim Stoß veranschaulicht. Das Elektron ruht vor dem Zusammenstoß.
Man kann die Masse des Photons als Anteil der Elektronenmasse einstellen. Zu Beginn beträgt sie 5% der Elektronenmasse.
Mit dem grünen Schieberegler kann man den Auftreffpunkt des Photons auf das Elektron verschieben.
- Warum ist der Effekt für Photonen mit größerer Wellenlänge, also kleinem Impuls zu vernachlässigen? Vergleichen Sie dazu den Zusammenstoß einer leichten und einer schweren Kugel mit einer ruhenden bei diesem Applet.
Photonen mit großer Wellenlänge haben eine im Vergleich zum Elektron kleine Masse. Daher werden sie beim Zusammenstoß mit dem Elektron mit fast dem gleichen Impulsbetrag reflektiert und die Wellenlänge ändert sich fast nicht. (So ähnlich wie ein Ball an einer Wand.)
Photonen von Röntgenlicht (ab 1nm) und noch kurzwelligerer Strahlung haben eine Masse von 2% und mehr der Elektronenmasse. Beim Zusammenstoß mit einem Elektron verändert sich der Impulsbetrag und damit die Wellenlänge merklich.