Gewichtskraft und Ortsfaktor: Unterschied zwischen den Versionen
Aus Schulphysikwiki
(→Massenanziehung (Gravitation)) |
(→Der Ortsfaktor g) |
||
| (2 dazwischenliegende Versionen des gleichen Benutzers werden nicht angezeigt) | |||
| Zeile 33: | Zeile 33: | ||
:Man gibt sie in Newton an: <math>F_G = 1\,\rm N</math> (auf der Erde!) | :Man gibt sie in Newton an: <math>F_G = 1\,\rm N</math> (auf der Erde!) | ||
::::::::<math>F_G = 0{,}16\,\rm N</math> (auf dem Mond!) | ::::::::<math>F_G = 0{,}16\,\rm N</math> (auf dem Mond!) | ||
| + | |} | ||
| + | |||
| + | ==Der Ortsfaktor <math>g</math>== | ||
| + | |||
| + | {|class="wikitable" style="border-style: solid; border-width: 4px " | ||
| + | | | ||
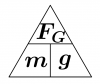
| + | [[Datei:Merkregel_Dreisatz_Fmg.png|thumb|100px]] | ||
| + | *Die Gewichtskraft <math>F_G</math> ist zur Masse <math>m</math> proportional. Bei der doppelten Masse hat man auch die doppelte Gewichtskraft. | ||
| + | *Das Verhältnis (oder Quotient) von Gewichtskraft und Masse beträgt auf der Erde ungefähr <math>9{,}81\,\rm \frac{N}{kg}</math>. Es gibt an mit wieviel Newton ein Kilogramm angezogen wird. Es heißt Ortsfaktor. | ||
| + | :<math>F_G = m\cdot g \qquad g= \frac{F_G}{m} \qquad m= \frac{F_G}{g} </math> | ||
|} | |} | ||
Aktuelle Version vom 6. Oktober 2024, 23:29 Uhr
Die Ausrüstung des Astronauts ist auf dem Mond "leichter" als auf der Erde.
Video: Astronaut mit einem Hammer auf dem Mond.
Inhaltsverzeichnis
Messung von Gewichtskräften
Mit einem Federkraftmesser kann man messen wie stark an etwas gezogen wird:
Ziehe an dem pinken Punkt!
Masse und Gewichtskraft
- Ein Kilogramm Mehl wird auch auf dem Mond nicht weniger, fühlt sich aber leichter an.
- Das Mehl wird weniger stark angezogen als auf der Erde, die Gewichtskraft des Mehls ist auf dem Mond kleiner.
- Man misst die Masse des Mehls in Kilogramm auf einer Balkenwaage.
- Man misst die Gewichtskraft des Mehls in Newton durch Verformung einer Stahlfeder in einem Kraftmesser.
|
Der Ortsfaktor [math]g[/math]
|
Links
- Praktikum Gewichtskraft (Thomas Unkelbach)
- Praktikum: Kraftmesser selbst bauen mit einem Gummiring. (Gymnasium Friedberg, Bayern)