*: Unterschied zwischen den Versionen
(→Leere Seite) |
(→Leere Seite) |
||
| (241 dazwischenliegende Versionen des gleichen Benutzers werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
==Leere Seite== | ==Leere Seite== | ||
{| | {| | ||
| − | |height=" | + | |height="960px"| |
| − | + | ||
|} | |} | ||
| − | = | + | ==Aufgaben zu Energieverlust und Wirkungsgrad== |
| − | + | '''1)''' "Ein Automotor hat einen Wirkungsgrad von ca. <math>1/3 \approx 33 \%</math>." | |
| + | :Was ist damit gemeint? | ||
| − | + | {| | |
| − | + | |style="vertical-align:top;"| | |
| − | : | + | '''2)''' In diesem Energieflussdiagramm ist der Weg der Energie bei einem Kohlekraftwerk dargestellt. |
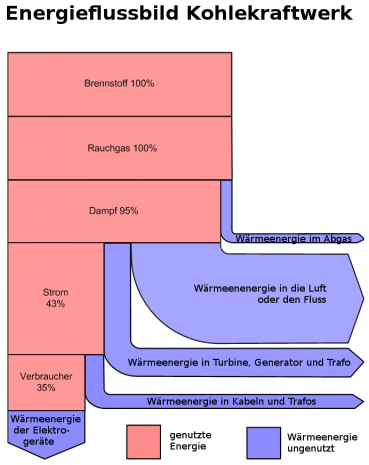
| − | :Bei | + | :'''a)''' Wie geht die meiste Energie der Kohle "verloren"? |
| − | + | :'''b)''' Welchen Wirkungsgrad hat das Kohlekraftwerk ohne Energietransport zum Verbraucher und mit Transport zum Verbraucher? | |
| − | + | :'''c)''' Bei einem Kraftwerk mit "Kraft-Wärme-Kopplung" werden die umliegenden Gebäude durch die Wärme des Kraftwerks geheizt und mit warmem Wasser versorgt. Durch große Rohre wird diese "Fernwärme" bis in die Häuser geleitet. Kleinere Anlagen werden auch "Blockheizkraftwerk" genannt. | |
| − | + | :Erkläre was der Vorteil der "Kraft-Wärme-Kopplung" gegenüber einem normalen Kraftwerk ist. Warum macht es einen Unterschied, ob es Sommer oder Winter ist? | |
| − | + | | | |
| − | + | [[Datei:Energieflussbild Kohlekraftwerk.png|369px]] | |
| − | + | ||
| − | + | ||
| − | + | ||
|} | |} | ||
| + | '''3)''' Werden viele Energieumlader zu einer Kette geschaltet, so berechnet sich der Gesamt-Wirkungsgrad, indem man alle einzelnen Wirkungsgrade multipliziert. ([[Energieverluste_und_der_Wirkungsgrad_von_Energiewandlern#Wirkungsgrad|Tabelle von Wirkungsgraden]]) | ||
| + | <br/>Fährt zum Beispiel ein Mensch Fahrrad, der vorher ein Brot gegessen hat, so wird die Energie zuerst von der Weizenpflanze von Licht auf das Weizenkorn umgeladen. Der Mensch lädt die Energie des Korns auf die Bewegung um: | ||
| − | + | [[Datei:Energieumladerkette_Vegetarier.png|514px]] | |
| − | + | :<math> 35\% \cdot 30\% = 0{,}35 \cdot 0{,}3 = 0{,}105 =10{,}5 \%</math> | |
| − | + | Der Wirkungsgrad beträgt insgesamt ca. 10%. Das heißt ca. 10% der Energie aus dem Sonnenlicht ist in der Bewegung angekommen. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | [[ | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | '''a)''' Berechne den Gesamt-Wirkungsgrad von: | |
| − | + | #einer Glühlampe, die von einem Kohlekraftwerk betrieben wird. | |
| − | ''' | + | #der Energieumladerkette der Dampfmaschine: Dampfmotor > Generator > Glühlampe. |
| − | + | ||
| − | : | + | '''b)''' Vergleiche den Wirkungsgrad von: |
| + | #einem Benzinauto mit einem Elektroauto, das den Akku mit einem Kohlekraftwerk lädt. | ||
| + | #einer Gasheizung mit einer Elektroheizung, die von einem Kohlekraftwerk angetrieben wird. | ||
| − | + | ==Energie im Haushalt== | |
| + | '''1) Energie sparen im Haushalt''' | ||
| − | + | In einem Haushalt braucht man Energie für die vielen elektrischen Geräte, wie Waschmaschine, Lampen, Computer,... und für die Heizung, das warme Wasser und für das Auto. | |
| + | |||
| + | *Zeichne ein Diagramm, aus dem hervorgeht, wofür ein durchschnittlicher Haushalt viel Energie benötigt und wofür weniger. (Infos im Artikel: [https://www.ndr.de/ratgeber/klimawandel/CO2-Ausstoss-in-Deutschland-Sektoren,kohlendioxid146.html Energiebedarf in Deutschland]) | ||
| − | + | ||
| − | + | '''2) Energiemengen und Kosten berechnen''' | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | Peters Schreibtischlampe hat eine Leistung von 20 Watt. Er schaltet sie am Tag ca. 2 Stunden an. Für eine Kilowattstunde Energie verlangt sein Stromanbieter 25 Cent. | |
| − | + | ||
| − | + | ||
| − | + | *Wieviel Energie benötigt man um die Lampe eine Sekunde, eine Minute oder eine Stunde anzuschalten? | |
| − | + | *Was kostet Peter die Schreibtischlampe pro Monat und pro Jahr? | |
| − | |||
| − | + | '''3) Verschiedene Lichtquellen''' | |
| − | + | Herbert mag das Licht von Energiesparlampen nicht und beleuchtet sein Wohnzimmer deshalb mit einer Glühlampe. Andrea hat sich dagegen für die gesamte Wohnung Energiesparlampen zugelegt, während Maria sich für LED-Lampen entschieden hat. | |
| − | + | *Vergleiche die verschiedenen Lampentypen bezüglich Energiebedarf, Wärmeentwicklung und Lebensdauer. | |
| − | + | Ein Glühwürmchen kann auch Licht produzieren und zwar mit einem Wirkungsgrad von über 90% | |
| + | *Was ist damit gemeint? | ||
| − | + | ==Fußnoten== | |
| + | <references /> | ||
Version vom 4. November 2024, 09:08 Uhr
Leere Seite
Aufgaben zu Energieverlust und Wirkungsgrad
1) "Ein Automotor hat einen Wirkungsgrad von ca. [math]1/3 \approx 33 \%[/math]."
- Was ist damit gemeint?
|
2) In diesem Energieflussdiagramm ist der Weg der Energie bei einem Kohlekraftwerk dargestellt.
|
3) Werden viele Energieumlader zu einer Kette geschaltet, so berechnet sich der Gesamt-Wirkungsgrad, indem man alle einzelnen Wirkungsgrade multipliziert. (Tabelle von Wirkungsgraden)
Fährt zum Beispiel ein Mensch Fahrrad, der vorher ein Brot gegessen hat, so wird die Energie zuerst von der Weizenpflanze von Licht auf das Weizenkorn umgeladen. Der Mensch lädt die Energie des Korns auf die Bewegung um:
- [math] 35\% \cdot 30\% = 0{,}35 \cdot 0{,}3 = 0{,}105 =10{,}5 \%[/math]
Der Wirkungsgrad beträgt insgesamt ca. 10%. Das heißt ca. 10% der Energie aus dem Sonnenlicht ist in der Bewegung angekommen.
a) Berechne den Gesamt-Wirkungsgrad von:
- einer Glühlampe, die von einem Kohlekraftwerk betrieben wird.
- der Energieumladerkette der Dampfmaschine: Dampfmotor > Generator > Glühlampe.
b) Vergleiche den Wirkungsgrad von:
- einem Benzinauto mit einem Elektroauto, das den Akku mit einem Kohlekraftwerk lädt.
- einer Gasheizung mit einer Elektroheizung, die von einem Kohlekraftwerk angetrieben wird.
Energie im Haushalt
1) Energie sparen im Haushalt
In einem Haushalt braucht man Energie für die vielen elektrischen Geräte, wie Waschmaschine, Lampen, Computer,... und für die Heizung, das warme Wasser und für das Auto.
- Zeichne ein Diagramm, aus dem hervorgeht, wofür ein durchschnittlicher Haushalt viel Energie benötigt und wofür weniger. (Infos im Artikel: Energiebedarf in Deutschland)
2) Energiemengen und Kosten berechnen
Peters Schreibtischlampe hat eine Leistung von 20 Watt. Er schaltet sie am Tag ca. 2 Stunden an. Für eine Kilowattstunde Energie verlangt sein Stromanbieter 25 Cent.
- Wieviel Energie benötigt man um die Lampe eine Sekunde, eine Minute oder eine Stunde anzuschalten?
- Was kostet Peter die Schreibtischlampe pro Monat und pro Jahr?
3) Verschiedene Lichtquellen
Herbert mag das Licht von Energiesparlampen nicht und beleuchtet sein Wohnzimmer deshalb mit einer Glühlampe. Andrea hat sich dagegen für die gesamte Wohnung Energiesparlampen zugelegt, während Maria sich für LED-Lampen entschieden hat.
- Vergleiche die verschiedenen Lampentypen bezüglich Energiebedarf, Wärmeentwicklung und Lebensdauer.
Ein Glühwürmchen kann auch Licht produzieren und zwar mit einem Wirkungsgrad von über 90%
- Was ist damit gemeint?