|
|
| (482 dazwischenliegende Versionen des gleichen Benutzers werden nicht angezeigt) |
| Zeile 1: |
Zeile 1: |
| | __NOTOC__ | | __NOTOC__ |
| − | ==Praktikum: Untersuchung einer schwingenden Stange (physikalisches Pendel)==
| + | {| |
| − | * Untersuchen Sie experimentell, wovon die Frequenz, bzw. die Schwingungsdauer einer Schaukel oder des Uhrenpendels abhängt.
| + | |height="900px"| |
| − | | + | |
| − | * Als vereinfachtes Modell der Schaukel oder des Uhrenpendels nehmen wir eine schwingende Stange. Wir nehmen also an, dass die Masse gleichmäßig ab dem Aufhängepunkt verteilt ist.
| + | |
| − | *Ein solches Pendel, bei dem der schwingende Körper nicht als Massepunkt vereinfacht wird, heißt auch "physikalisches Pendel".
| + | |
| − | | + | |
| − | Mögliche Beeinflussungen durch:
| + | |
| − | | + | |
| − | * halbe Stangenlänge l (Die halbe Stangenlänge entspricht dem Abstand zwischen Drehpunkt und Schwerpunkt. So läßt sich das Ergebnis besser mit dem Fadenpendel vergleichen.)
| + | |
| − | * Masse <math>m</math>
| + | |
| − | * Amplitude <math>\hat y</math>
| + | |
| − | * Reibung
| + | |
| − | * Antrieb
| + | |
| − | Man darf immer nur eine Größe variieren und dann jeweils die Periode messen. Misst man z.B. für verschiedene Amplituden die Periode erhält man einen Zusammenhang zwischen Amplitude und Periodendauer, der streng genommen nur für die gewählte Länge, Masse usw. gilt.
| + | |
| − | <br>Ändert sich die Periode bei Variation einer Größe nicht, so ist sie davon unabhängig.
| + | |
| − | | + | |
| − | Den Zusammenhang zwischen der Periodendauer und der Reibung bzw. des Antriebs kann man mit diesem Versuchsaufbau nicht untersuchen.
| + | |
| − | | + | |
| − | ;Aufbau:
| + | |
| − | [[Bild:Schwingender_Stab_Versuchsaufbau.jpg|thumb|right|Der schwingende Stab]]
| + | |
| − | | + | |
| − | Mittels einer Klemme wird eine Stange senkrecht an einem Tisch angebracht. An dieser Stange wird ein Geodreieck sowie eine kleinere, senkrecht zur Ersten stehenden Stange befestigt. Das Geodreieck hat die Funktion, die Amplitude zu messen und wird daher so angebracht, dass die längere Seite oben ist und und die auf das Geodreieck aufgetragene Senkrechte genau auf der Stange verläuft.
| + | |
| − | An der Querstange wird nun die bewegliche Stange aufgehängt.
| + | |
| − | | + | |
| − | ;Beobachtung/Messwerte:
| + | |
| − | | + | |
| − | *Abhängigkeit von der Masse m:
| + | |
| − | :Durch Zusammenkleben zweier gleicher Stangen kann man die Masse verdoppeln.
| + | |
| − | | + | |
| − | halbe Stangenlänge <math>l \rm \text{ in } m</math>:
| + | |
| − | | + | |
| − | Amplitude <math>\hat y \rm \text{ in } ^{\circ} </math>:
| + | |
| − | | + | |
| − | {| class="wikitable" | + | |
| − | |- | + | |
| − | | <math>m \rm \text{ in } kg</math>
| + | |
| − | | style="height:30px; width:80px;" |
| + | |
| − | | style="height:30px; width:80px;" |
| + | |
| − | |-
| + | |
| − | |<math>10 \, T \rm \text{ in } s</math>
| + | |
| − | | style="height:30px; width:80px;" |
| + | |
| − | | style="height:30px; width:50px;" |
| + | |
| − | |-
| + | |
| − | |<math>T \rm \text{ in } s</math>
| + | |
| − | | style="height:30px; width:80px;" |
| + | |
| − | | style="height:30px; width:50px;" |
| + | |
| | |} | | |} |
| | + | ==Das Potential im elektrischen Stromkreis== |
| | | | |
| − | *Abhängigkeit von der halben Stangenlänge l:
| + | ====Übertragung des Drucks im Wasserstromkreis auf den elektrischen Stromkreis==== |
| | + | Der Druck im Wasserstromkreis entspricht dem elektrischen Potential <math>\varphi</math>. Es wird in Volt (nach [https://de.wikipedia.org/wiki/Alessandro_Volta Alessandro Volta] 1745-1827) gemessen. |
| | | | |
| − | Masse <math>m \rm \text{ in } kg</math>:
| + | {|class="wikitable" style="border-style: solid; border-width: 4px " |
| − | | + | | |
| − | Amplitude <math>\hat y \rm \text{ in } ^{\circ} </math>:
| + | *Die Batterie erzeugt hinter sich ein hohes Potential und vor sich ein geringes Potential. |
| − | | + | *Dieser Potentialunterschied treibt den elektrischen Strom an. Die Elektrizität fließt vom hohen Potential zum niedrigen Potential. |
| − | {| class="wikitable" | + | *Bei einer Verzweigung ändert sich das Potential nie! |
| − | |-
| + | *Bei einem Lämpchen (oder einem anderem Widerstand) kann das Potential abfallen. |
| − | ||<math>l \rm \text{ in } m</math>
| + | |
| − | | style="height:30px; width:80px;" |
| + | |
| − | | style="height:30px; width:80px;" |
| + | |
| − | | style="height:30px; width:80px;" |
| + | |
| − | | style="height:30px; width:80px;" |
| + | |
| − | | style="height:30px; width:80px;" |
| + | |
| − | | style="height:30px; width:80px;" |
| + | |
| − | |-
| + | |
| − | |<math>10 \, T \rm \text{ in } s</math>
| + | |
| − | | style="height:30px; width:80px;" |
| + | |
| − | | style="height:30px; width:50px;" |
| + | |
| − | | style="height:30px; width:50px;" |
| + | |
| − | | style="height:30px; width:50px;" |
| + | |
| − | | style="height:30px; width:50px;" |
| + | |
| − | | style="height:30px; width:50px;" |
| + | |
| − | |-
| + | |
| − | |<math>T \rm \text{ in } s</math>
| + | |
| − | | style="height:30px; width:80px;" |
| + | |
| − | | style="height:30px; width:50px;" | | + | |
| − | | style="height:30px; width:50px;" |
| + | |
| − | | style="height:30px; width:50px;" |
| + | |
| − | | style="height:30px; width:50px;" |
| + | |
| − | | style="height:30px; width:50px;" |
| + | |
| − | |-
| + | |
| − | |<math> \frac{T}{l} \text{ in } {\rm \frac{s}{m} }</math>
| + | |
| − | | style="height:30px; width:80px;" |
| + | |
| − | | style="height:30px; width:50px;" |
| + | |
| − | | style="height:30px; width:50px;" |
| + | |
| − | | style="height:30px; width:50px;" |
| + | |
| − | | style="height:30px; width:50px;" |
| + | |
| − | | style="height:30px; width:50px;" |
| + | |
| − | |-
| + | |
| − | |<math> \frac{T}{l^2} \text{ in } {\rm \frac{s}{m^2} }</math>
| + | |
| − | | style="height:30px; width:80px;" |
| + | |
| − | | style="height:30px; width:50px;" |
| + | |
| − | | style="height:30px; width:50px;" |
| + | |
| − | | style="height:30px; width:50px;" |
| + | |
| − | | style="height:30px; width:50px;" |
| + | |
| − | | style="height:30px; width:50px;" |
| + | |
| − | |-
| + | |
| − | |<math> \frac{T}{\sqrt{l}} \text{ in } {\rm \frac{s}{\sqrt{m}} }</math>
| + | |
| − | | style="height:30px; width:80px;" |
| + | |
| − | | style="height:30px; width:50px;" |
| + | |
| − | | style="height:30px; width:50px;" |
| + | |
| − | | style="height:30px; width:50px;" |
| + | |
| − | | style="height:30px; width:50px;" |
| + | |
| − | | style="height:30px; width:50px;" |
| + | |
| | |} | | |} |
| | | | |
| − | *Abhängigkeit von der Amplitude <math>\hat y</math>:
| + | ====Messen des Potentialunterschiedes: die Spannung <math>U</math>==== |
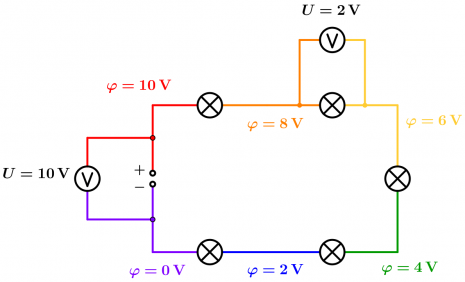
| | + | Wie misst man das Potential an einer Stelle eines Stromkreises? Verbindet man mit einem Kabel ein sogenanntes Voltmeter mit der Stelle, so passiert nichts! Man benötigt auch noch ein zweites Kabel. Das Voltmeter kann nämlich nur Potential''unterschiede'' zwischen zwei Stellen messen! |
| | | | |
| − | Masse <math>m \rm \text{ in } kg</math>:
| + | Deswegen legt man das Potential einer beliebigen Stelle als neutral, also <math>0\,\rm V</math> , fest. An diese Stelle wird eines der beiden Kabel gesteckt. Steckt man das andere Kabel an eine andere Stelle, so zeigt das Voltmeter den Unterschied zu <math>0\,\rm V</math> , also das dortige Potential, an. |
| | | | |
| − | halbe Stangenlänge <math>l \rm \text{ in } m</math>:
| + | [[Datei:Stromkreis Spannungsmessung Voltmeter.png|465px]] |
| | | | |
| − | {| class="wikitable" | + | {|class="wikitable" style="border-style: solid; border-width: 4px " |
| − | |-
| + | | |
| − | |<math>\hat y \rm \text{ in } ^{\circ} </math>
| + | *Ein Voltmeter kann nur den Potentialunterschied <math>\Delta \varphi</math> messen. Er heißt "Spannung" (<math>U</math>) und wird auch in Volt gemessen. |
| − | | style="height:30px; width:80px;" | 5°
| + | *Das Potential <math>0\,\rm V</math> kann man an eine beliebige Stelle legen. Meistens ist es der Minuspol ("Masse" oder "Erde"). |
| − | | style="height:30px; width:80px;" | 10°
| + | |
| − | | style="height:30px; width:80px;" | 20°
| + | |
| − | | style="height:30px; width:80px;" | 40°
| + | |
| − | | style="height:30px; width:80px;" | 60°
| + | |
| − | | style="height:30px; width:80px;" | 80°
| + | |
| − | |-
| + | |
| − | |<math>10 \, T \rm \text{ in } s</math>
| + | |
| − | | style="height:30px; width:80px;" |
| + | |
| − | | style="height:30px; width:50px;" | | + | |
| − | | style="height:30px; width:50px;" |
| + | |
| − | | style="height:30px; width:50px;" |
| + | |
| − | | style="height:30px; width:50px;" |
| + | |
| − | | style="height:30px; width:50px;" |
| + | |
| − | |-
| + | |
| − | |<math>T \rm \text{ in } s</math>
| + | |
| − | | style="height:30px; width:80px;" |
| + | |
| − | | style="height:30px; width:50px;" |
| + | |
| − | | style="height:30px; width:50px;" |
| + | |
| − | | style="height:30px; width:50px;" |
| + | |
| − | | style="height:30px; width:50px;" |
| + | |
| − | | style="height:30px; width:50px;" |
| + | |
| − | |-
| + | |
| − | |<math> \frac{T}{\hat y} \text{ in } {\rm \frac{s}{\circ} }</math>
| + | |
| − | | style="height:30px; width:80px;" |
| + | |
| − | | style="height:30px; width:50px;" |
| + | |
| − | | style="height:30px; width:50px;" |
| + | |
| − | | style="height:30px; width:50px;" |
| + | |
| − | | style="height:30px; width:50px;" |
| + | |
| − | | style="height:30px; width:50px;" |
| + | |
| − | |-
| + | |
| − | |<math> \frac{T}{\hat y^2} \text{ in } {\rm \frac{s}{\circ ^2} }</math>
| + | |
| − | | style="height:30px; width:80px;" |
| + | |
| − | | style="height:30px; width:50px;" |
| + | |
| − | | style="height:30px; width:50px;" |
| + | |
| − | | style="height:30px; width:50px;" |
| + | |
| − | | style="height:30px; width:50px;" |
| + | |
| − | | style="height:30px; width:50px;" |
| + | |
| − | |-
| + | |
| − | |<math> \frac{T}{\sqrt{\hat y}} \text{ in } {\rm \frac{s}{\sqrt{\circ}} }</math>
| + | |
| − | | style="height:30px; width:80px;" |
| + | |
| − | | style="height:30px; width:50px;" |
| + | |
| − | | style="height:30px; width:50px;" |
| + | |
| − | | style="height:30px; width:50px;" |
| + | |
| − | | style="height:30px; width:50px;" |
| + | |
| − | | style="height:30px; width:50px;" |
| + | |
| | |} | | |} |
| − |
| |
| − | ;Erklärung/Auswertung:
| |
| − |
| |
| − | Die gemessenen Zusammenhänge werden jeweils in ein Koordinatensystem gezeichnet. Man trägt zum Beispiel die Periodendauer (y-Achse) über die halbe Stangenlänge (x-Achse) auf.
| |
| − |
| |
| − | Um einen rechnerischen Zusammenhang zwischen den Größen zu finden, sucht man nach konstanten Quotienten oder Produkten der Messgrößen. Diese werden in die Tabelle eingetragen.
| |
| − |
| |
| − | Als Beispiel hier der Zusammenhang zwischen Periodendauer und Pendellänge. Es kommen mehrere Möglichkeiten in Betracht:
| |
| − | #<math>T = c \cdot l \quad \Leftrightarrow \quad c = \frac{T}{l}</math>
| |
| − | #<math>T = c \cdot l^2 \quad \Leftrightarrow \quad c = \frac{T}{l^2}</math>
| |
| − | #<math>T = c \cdot \sqrt{l} \quad \Leftrightarrow \quad c = \frac{T}{\sqrt{l}}</math>
| |
| − |
| |
| − | Man berechnet daher alle Quotienten und untersucht, ob ein Quotient für alle Messungen ungefähr gleich bleibt. Wenn dies der Fall ist, so nimmt man den Mittelwert der Quotienten, um damit eine Formel aufzustellen.
| |