*: Unterschied zwischen den Versionen
Aus Schulphysikwiki
| (477 dazwischenliegende Versionen des gleichen Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
__NOTOC__ | __NOTOC__ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{| | {| | ||
| − | | | + | |height="900px"| |
| − | + | |} | |
| − | | | + | ==Das Potential im elektrischen Stromkreis== |
| − | + | ====Übertragung des Drucks im Wasserstromkreis auf den elektrischen Stromkreis==== | |
| − | + | Der Druck im Wasserstromkreis entspricht dem elektrischen Potential <math>\varphi</math>. Es wird in Volt (nach [https://de.wikipedia.org/wiki/Alessandro_Volta Alessandro Volta] 1745-1827) gemessen. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| + | {|class="wikitable" style="border-style: solid; border-width: 4px " | ||
| + | | | ||
| + | *Die Batterie erzeugt hinter sich ein hohes Potential und vor sich ein geringes Potential. | ||
| + | *Dieser Potentialunterschied treibt den elektrischen Strom an. Die Elektrizität fließt vom hohen Potential zum niedrigen Potential. | ||
| + | *Bei einer Verzweigung ändert sich das Potential nie! | ||
| + | *Bei einem Lämpchen (oder einem anderem Widerstand) kann das Potential abfallen. | ||
|} | |} | ||
| − | + | ====Messen des Potentialunterschiedes: die Spannung <math>U</math>==== | |
| − | + | Wie misst man das Potential an einer Stelle eines Stromkreises? Verbindet man mit einem Kabel ein sogenanntes Voltmeter mit der Stelle, so passiert nichts! Man benötigt auch noch ein zweites Kabel. Das Voltmeter kann nämlich nur Potential''unterschiede'' zwischen zwei Stellen messen! | |
| − | + | ||
| − | + | Deswegen legt man das Potential einer beliebigen Stelle als neutral, also <math>0\,\rm V</math> , fest. An diese Stelle wird eines der beiden Kabel gesteckt. Steckt man das andere Kabel an eine andere Stelle, so zeigt das Voltmeter den Unterschied zu <math>0\,\rm V</math> , also das dortige Potential, an. | |
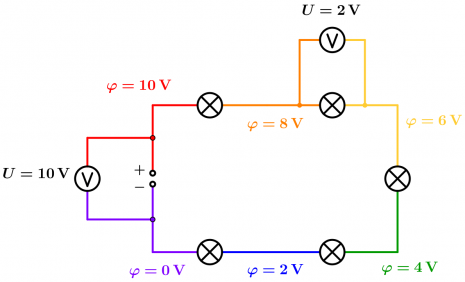
| − | + | [[Datei:Stromkreis Spannungsmessung Voltmeter.png|465px]] | |
| − | + | {|class="wikitable" style="border-style: solid; border-width: 4px " | |
| − | + | | | |
| − | + | *Ein Voltmeter kann nur den Potentialunterschied <math>\Delta \varphi</math> messen. Er heißt "Spannung" (<math>U</math>) und wird auch in Volt gemessen. | |
| − | + | *Das Potential <math>0\,\rm V</math> kann man an eine beliebige Stelle legen. Meistens ist es der Minuspol ("Masse" oder "Erde"). | |
| − | + | |} | |
| − | + | ||
| − | * | + | |
| − | + | ||
Version vom 9. April 2025, 07:28 Uhr
Das Potential im elektrischen Stromkreis
Übertragung des Drucks im Wasserstromkreis auf den elektrischen Stromkreis
Der Druck im Wasserstromkreis entspricht dem elektrischen Potential φ. Es wird in Volt (nach Alessandro Volta 1745-1827) gemessen.
|
Messen des Potentialunterschiedes: die Spannung U
Wie misst man das Potential an einer Stelle eines Stromkreises? Verbindet man mit einem Kabel ein sogenanntes Voltmeter mit der Stelle, so passiert nichts! Man benötigt auch noch ein zweites Kabel. Das Voltmeter kann nämlich nur Potentialunterschiede zwischen zwei Stellen messen!
Deswegen legt man das Potential einer beliebigen Stelle als neutral, also 0V , fest. An diese Stelle wird eines der beiden Kabel gesteckt. Steckt man das andere Kabel an eine andere Stelle, so zeigt das Voltmeter den Unterschied zu 0V , also das dortige Potential, an.
|