Energietransport einer Welle (Intensität): Unterschied zwischen den Versionen
(→Lineare Welle) |
(→Intensitätsrückgang bei Kugel-, Kreis- und Zylinderwellen) |
||
| Zeile 30: | Zeile 30: | ||
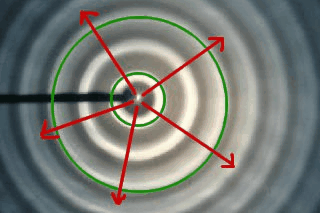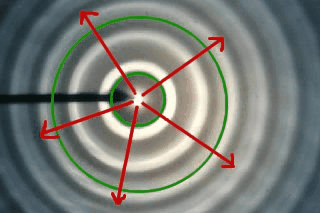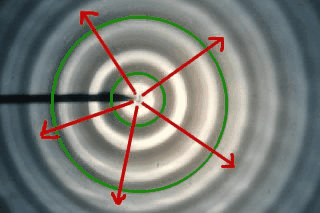
==Intensitätsrückgang bei Kugel-, Kreis- und Zylinderwellen== | ==Intensitätsrückgang bei Kugel-, Kreis- und Zylinderwellen== | ||
| − | + | [[Datei:Welle_Kreiswelle_animiert.gif|right|framed|Bei der Kreiswelle verteilt sich der Energiefluss auf immer größere Kreise.]] | |
| − | + | Anders als bei einer ebenen Welle verteilt sich mit zunehmendem Abstand von der Quelle die Energie immer mehr im Raum. Das heisst, dass die Intensität mit dem Abstand zur Quelle sinkt. | |
| + | |||
| + | Eine annähernd punktförmige Quelle, die mit z.B. 5 Watt Leistung sendet, verteilt diesen Energiestrom auf eine immer größere Kugelfläche. Die Energiemenge pro Zeit ist für jede Fläche ist konstant! Für die einzelnen Wellen ergibt sich daraus die Intensität in einem Abstand r von der Quelle: | ||
| + | |||
| + | *Kreiswelle: Die Leistung P verteilt sich auf einen Kreis. | ||
| + | :<math>I(r)= \frac{P}{2 \ \Pi \ r} \quad \sim \frac{1}{r}</math> | ||
| + | *Kugelwelle: Die Leistung verteilt sich auf eine Kugeloberfläche. | ||
| + | :<math>I(r)=\frac{P}{4 \ \Pi \ r^2} \quad \sim \frac{1}{r^2}</math> | ||
| + | *Zylinderwelle: Die Leistung verteilt sich auf einen Zylindermantel der Länge l mit dem Radius r. | ||
| + | :<math>I(r,l)= \frac{P}{2 \ \Pi \ r \ l} \quad \sim \frac{1}{r}</math> | ||
| + | |||
| + | |||
| + | |||
*und wie die Amplitude? | *und wie die Amplitude? | ||
Version vom 9. Februar 2011, 13:26 Uhr
Unter der Intensität einer Welle versteht man bei einer dreidimensionalen Welle die Stärke des Energiestroms pro Fläche. Sie gibt also an, wieviel Energie pro Zeit und pro Fläche transportiert wird.
Im Falle einer zweidimensionalen Welle ist die Intensität die Leistung pro Länge.
Im Falle einer eindimensionalen Welle ist es einfach die Leistung.
Inhaltsverzeichnis
Beispiele
- Hängt der Lärm vom Wetter ab? Dämpfung, Brechung, Streuung, Beugung und Reflexion von Schallwellen im Hinblick auf Lärmberuhigung. (DLR Institut für Physik der Atmosphäre)
Ebene Welle
Um die Intensität einer ebenen Welle zu bestimmen, betrachtet man ein quaderförmiges Raumgebiet mit der Stirnfläche A und der Länge x = ct. In der Zeit t wird also die Fläche A von der in diesem Gebiet enthaltenen Energie durchströmt.
Die enthaltene Energie kann man über die in den Schwingungen gespeicherte Energie bestimmen:
[math]E = \frac{M}{2}\omega^2 \hat y^2[/math]
Die Masse berechnet man aus Dichte und Volumen:
[math]E = \frac{\rho V}{2}\omega^2 \hat y^2[/math]
Das Volumen aus Fläche A und Länge x:
[math]E = \frac{\rho A c t}{2}\omega^2 \hat y^2[/math]
Für die Energie pro Zeit und Fläche folgt daher:
[math]I = \frac{1}{2} \ \rho \ c \ \omega^2 \hat y^2[/math]
Die Intensität ist proportional zur Dichte des Mediums, zur Ausbreitungsgeschwindigkeit,
zum Quadrat der Frequenz und zum Quadrat der Amplitude!
Intensitätsrückgang bei Kugel-, Kreis- und Zylinderwellen
Anders als bei einer ebenen Welle verteilt sich mit zunehmendem Abstand von der Quelle die Energie immer mehr im Raum. Das heisst, dass die Intensität mit dem Abstand zur Quelle sinkt.
Eine annähernd punktförmige Quelle, die mit z.B. 5 Watt Leistung sendet, verteilt diesen Energiestrom auf eine immer größere Kugelfläche. Die Energiemenge pro Zeit ist für jede Fläche ist konstant! Für die einzelnen Wellen ergibt sich daraus die Intensität in einem Abstand r von der Quelle:
- Kreiswelle: Die Leistung P verteilt sich auf einen Kreis.
- [math]I(r)= \frac{P}{2 \ \Pi \ r} \quad \sim \frac{1}{r}[/math]
- Kugelwelle: Die Leistung verteilt sich auf eine Kugeloberfläche.
- [math]I(r)=\frac{P}{4 \ \Pi \ r^2} \quad \sim \frac{1}{r^2}[/math]
- Zylinderwelle: Die Leistung verteilt sich auf einen Zylindermantel der Länge l mit dem Radius r.
- [math]I(r,l)= \frac{P}{2 \ \Pi \ r \ l} \quad \sim \frac{1}{r}[/math]
- und wie die Amplitude?
Energie"verlust" durch Dämpfung
- Durch Reibung entsteht Wärme (Entropie).
- Wie groß ist der Effekt?
- Beispielrechnung für eine Schallwelle. Wie weit kann man sie hören, wenn sie mit 5Watt sendet?
- Rechner zur bestimmung der Dämpfung in db/m in Abhängigkeit von Temperatur, Luftfeuchtigkeit und Frequenz. (Thomas Jahnke)
Empfundene Lautstärke
- Wikipedia:Lautstärke
- Schluss mit Lärm! (Europäische Woche für Sicherheit und Gesundheit bei der Arbeit)
- Schalldruck p ist der Differenzdruck zum Normaldruck (P(t) kann zB. sinusförmig sein, dann ist der effektive Unterschied zum Normaldruck [math]\hat p / \sqrt{2}[/math].
- Es gilt Intensität=Ausbreitungsgeschwindigkeit * Schalldruck