Materiewellen nach de Broglie: Unterschied zwischen den Versionen

Aus Schulphysikwiki
Wechseln zu: Navigation, Suche
(→‎Elektronenbeugung Debey-Scherrer-Verfahren)
(→‎Animation: Braggsche Reflektionsbedingung)
Zeile 7: Zeile 7:
  
 
====Animation: Braggsche Reflektionsbedingung====
 
====Animation: Braggsche Reflektionsbedingung====
 +
Dargestellt sind zwei Atomebenen im Abstand d.
 
<ggb_applet width="736" height="633"  version="4.0" ggbBase64="UEsDBBQACAgIAAtpPkIAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIAAtpPkIAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7V3bctvGGb5OnmLLi4ydmBR2F4tDIiUjyZatWLQzsZvptJPJgMSSggUCDABKpCYXveq0T9HbXjfvkbxDnqT/7gI8ASABkpKopBzLOO3x+/7THggefjUe+OiaR7EXBkcN3NIaiAfd0PWC/lFjlPSaVuOrLz8+7POwzzuRg3phNHCSo4YuUnruUYMQammuxZo6sTpNvdfrNTvcIE2NUkxc28Zd2msgNI69z4PwjTPg8dDp8nfdSz5wLsKuk8iKL5Nk+PnBwc3NTSurqhVG/YN+v9Max24DQTOD+KiRnnwOxS1kuqEyOdE0fPCX9oUqvukFceIEXd5Aogsj78uPPzq88QI3vEE3nptcHjVMXW+gS+71L6FPpmE10IFINARAhrybeNc8hqxzl7LPyWDYkMmcQDz/SJ0hf9qdBnK9a8/l0VFDazHbME0d25TpFrVM3EBh5PEgSdPitM6DrLTDa4/fqGLFmawRWpmEod9xRInop58Q0YiGnokDVgcCB8NQjzR1T6PqQNRBVwem0ugqu66S6iqNrtLotIGuvdjr+Pyo0XP8GBD0gl4E7E2v42Tic9me9Mas9/gZ9Cn2biEx1UBMFORwX9OeiT8D/nTx4GCxk3iu1iQa1aw0q9KkRvUqyVYdpVmduhCj5ToJK+mmsaJS1e8q/cRsDlqoSv6Tf7ka6apuLteorrer0NDvpYuHB5mqHKbageJLkTaVnoQPYqEv1EbMFmKPEQPdMEyQcoawDQeTINAGhBnSGVxiCxniaCJqwgMdUWQhkQ5TJJWDWfCfbsrCDMSgMHHXBJ1EGCrSEaMIS53SEWgSknoJOkoopGAMMcgkqsdEFEENpBtwRS2kQxuFSpoYElLICNdQPUEUIyoyYxMRAxmiPKwLVTcs0XQokiBDQwYWBYJWg0YrbYb0FqKiN0YKlxcMR8kCRN2Bm50m4XDKBaQGezSzeso+LRjFjw59p8N98BPvBJMIXTu+0AhZUS8MEpSRSNS9fuQML71u/I4nCeSK0Qfn2rlwEj4+g9RxVrdM2w2D+JsoTE5DfzQIYoS6oa9N2xz6eO6cTFsNF3TugT7/gM09MObOzcJ6Q3iCRjGH+sMozpI7rnsuUsxMAyD5NvAnJxF3roaht9iNwwPpcg75qOt7rucE34GwiloELmjqgYS5yjyQobGsIWHkvpvEIMFo/FcehWCqTPC58x/IN0kfYday5z9Cg7qOUD7dXnwCHm5S+khWza+nDDljPutsPxKaPXdxHp+E/uyW7P+pM0xGkQweQEcj0avjoO9zKSPS3IJn7l51wvE7JRxUlfV+MuQii2xBpy9xR2AbCGOQID121FGmEU2bptJkGk2m0DJp89zpc2wTmUIeO+ooU4H4qqalXcVZN7GWVePF0qJpjVRvMmslhF84+lHgJRfZReJ1r9KuYpXhzWjQ4VMRWiwT76rMw4MlGTu84lHA/VSkgcxROIqVhs5Ju8u73gAu1YMUEkfQ9WdogLrr8n7Es4b7MjBTgMmn2ry05m7Los6icHAeXL8HWVhqwOFB1srDuBt5QyFzqANu4IrPpMr1Yge8iDufT+ggdL0rvAXAkwhoTiKn329+y3s+vxL3QVtHyWUI5H/jJBFAiN5AGwdOEIBmXI784eUk9q5uvCuv5YpqwA4B2EJbfT6A4AwlUiKlUE+ZeSOjPkEBCjsfwBQuUzcHLiQolE8pyQ7U74jYMEXKdyY8WqBBFtgO3WVEgTDZbbAMQyUQQ86VLKkWw8kQipMquGDZoPsxGosY3wLvPDlqNI2WCFtuVdiv4l7RXaGZC9Zc3V2iF2ROIZXDLBgNOCA+BcWXqEHOUZqftFIlXkAyjTtUnpm2zOM4tQaanur6DEmcQ1IrRDJNF/siPEcDL1DtQQMHsBHUdGJwOgmMUEDug9kIRTUvNdoQ3onxD+Sw5JAJ0GSGPOt5Yz51qSB/3i3on7PQo5nRScAfXkHQH8tQMkltoDx55bkuD6bNXSZe9DdHvVZE/TxP3XAAGuCiQMZh30jZnsUFDnjY8TEYpxT4UZLdPVEFpdnXKMlJXkkWqK2gI9pKDSnmdYca0sw4lSTvQD/W4z4pxP1VHdxfbWicMFFKJY8VDNSdw6+l6JOWiFZ2Dv95kIDzBHwKRR85uIyN0zpsnD6oFuTBbN6fLBfbkOM66B0/fhtC7tSGnHpR1+fHUXcJ+1MlwK/gQFLMF1jgq1mAyMrrDp1oxgTfQcizBRWFvpKs9pUwluLBNTQVhm4IjbV0WnOiZWRkd8Y404sJTm/d4jmmBiJyHKPjLP1xluoYsG1aLcsSccgxTcs91rPijtlcV/mPgepBrIJ4bzD0va6XTLnxhRhNrRKIXT5Sv+J8KIZIb4P3kRPEYhJWpZkbAWytoc/raOjzR6+h9+/ki2F/UQf2F48e9ru1i9VhP6sD+9mjh53uCewv68D+8tHD3tw17quH2u7yUJtm1dUdapdPWWwx0NbSYTatPcw2jWyYrbGHHmYXkl6uG9/JSGRJOZ5oz5D2VAVr4rzpPs2pyvVqVVERzpTG64cN1ApGHDQV+VlZGwRzc1OLafzUhfCUx54TpPKVwLW0P2i+9iV9K6dHBlS+k/Alhl4qcq7zFuwTZxjGX9SyY2mW/RgSTm3SlKHdOoMyRI/LED2uj+jxfiFKHgbRkzJET+ojerJfiOKHQfS0DNHT+oie7hWiObN8P4A+LwP0eX1An+8VoA8koS/KAH1RH9AXewXoAxnRszJAz+oDerZXgN6xny8a9PEciud18DvfBjnMaAXs7nx9FYIBE5s20bBh67pJxGa6icCeELinGdiyCCY6vgNGvnUmxf7sPEeLs5qWCErKQHc2I2XVYu02cUEOxkkx5mtHHmzNNPLDzttuGqH8gDeIUSDTZqNHsdGvrw4ddXi0kcp5GbDn9f3AeZkfuP8V2bWGCVTKNE3bsqmFsWmZzL4fyzSVPGWhZiAv2qkq4C9Yq21c8B7YrKbVAkdmGhrTLKpjk1iP1oS1vSjKzXydrlxiT4WCbGLDyB7asLuZbi8E9nwVsOebOIfzLZ3DHdmxavGVZt6rGSMLZuwHXGbI1jFQYMqK8C8zZt0wcD0VwIq9yWnqgTPG6Ld//Rtp6Ld//kfMwZPFS6outzWIeEODKLiaFBL7yIO4Ygu46PmKFfbrOor69R5ZPojaDJPaukZtU9eJxmz9RVN85eXuIrpic5jGAeuN4sbh3T4GeVVjPHov1vHrBau4OsTbMNCrG+79viwkkTT+fkLGt1FyGfbDwPEvoPHFoaNTIked1bIj0JgKRGdfVktL9bVotqi51VLqKmp3wkgJL70avPT2hZf86IwUM5PGmQ/ATNlGZmfe83VydLyu4+le30dksXJKdo4Su2Ub1LawTXQG6JvpMJq0sIGJqWGd6IZOLZbaRLE9c/ZtObJDR7cG+Xn8ezn8L+rgf7FHkd0S/IZdjL9dCD/dIfzveF/cL7ZFr3OA91cDHqelZYj292T1hrR0mzFiYGzppkYtMnUNWBggG55iYhBs0Sq+YbrxCe+l319J6UWO0st6lF7uK6XpzMUSoRUcyqOk87Wi87QkTujWI7W73RTvTrdWMA1iBGpZmBHbwKZZzKtSVNqiBoTqlm5BzG4ZjNFHG62XaO28/8vrrlePZu/uaa4afyzzbOEV+rtMM2WPiGY+HkbQMDFKznYWxw0Ed4FQHvSTy791v0efofTc+169MWLN3uQ4/z1g3dAgaNAM3YQ4mlG9ug3G65ssxvRpo6NwFLhPKPoUPfFRE7nx06foANEqzZalLDV8KkQbtbTqmn3pVPKH6pMkH/bE8+1yync6mCJ7oi0V1wiqzIVdVaf26lFSW2eqas+JLtr/5OQYbdcZ7rXvaTL57jdB6S1m6pgyS7OIzXTTZqlQaMxglhhEWiaEwCa7g3nowm9ctMt2Qo1WE7T0NYvRfWwsqBiQ4JbFIN5gBkQkOowPDTP7qjfoFjNNYEBjzLQNY/uFtDrfw5Aut72ao7JdOKOyXTijKusDy2Td316QPzBl7TLK2vVX1tr3uqZWNfAvMWbAmq2DF8OWZsIQwDbI/VmzgpAih/9NLWW5+b+aVFSTebHe/RadWnufZpn2SmMecItOIfDt9ZsB2ptuBmg/wGaAijRUtVt3sRmgmIcKDNTbozbL9BiQz4W/9+UvZnZCEtAunVu4reUzbh/Lvovt/E7O7egP4HaW/MMm9M9bwZy9WxCDQS0xGPxBxYA8nBhUiUGKp+ffKP7foM/QEzeWryFYZt+N1wQhy5P0IsNW0eMOp+lnr49bnF1OX3XJWpbOMNVs07CppjN9c+4eeP7pbBTIQpf4jb3gCUGfol//Lqa7x6iJxk/eyPlu/ylwPoELJQFjdUbUGTwSufz8KIL7/prXhvWylkzHEjLPQ48n6nO6dkGB5BcUJGr1FxVIfjXEWPyw6pO31RpP842nmzWeLjee7XBFRL4wumTpWMlr2QryL/9dLafyhcTTfkDqpV5oLZ0QRjFjVLeEjbBT67DDb6QStgMhXrOfzIm6syhSz6Z1fT+8kS9IHkuEq5qZIjoWVjRSUvIrvb/8XIuOn9fSYdH/01FEx/kCES9zRPz6jzpEQOrVROB1LKx6pdQGJLzt9WKeqJm4dM/ZnlGUN7fv+TjJVp8/+XEUJl+0nbE3GA0QBAMQEKC3kRuMgv6f1MNG3uwmUEJjsbidRdnVbXVNlxtDH2QocCyw424u3pG/DBGDP+nNfkVB/hKA1sjCqEy8Fl/shFt2ugNXb2FS9m6nYiJIIRG3N9zbjIkawW4pE+RRMzH/OxSYznhZuF/tBVwVNhGd5ixaUG98Emy/Vr6rtYTlFwJW3Oe3JyOQg/nfXhDX2a91ffk/UEsHCPpmJxxADgAASmwAAFBLAQIUABQACAgIAAtpPkLWN725GQAAABcAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAICAgAC2k+QvpmJxxADgAASmwAAAwAAAAAAAAAAAAAAAAAXQAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAADXDgAAAAA=" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />
 
<ggb_applet width="736" height="633"  version="4.0" ggbBase64="UEsDBBQACAgIAAtpPkIAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIAAtpPkIAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7V3bctvGGb5OnmLLi4ydmBR2F4tDIiUjyZatWLQzsZvptJPJgMSSggUCDABKpCYXveq0T9HbXjfvkbxDnqT/7gI8ASABkpKopBzLOO3x+/7THggefjUe+OiaR7EXBkcN3NIaiAfd0PWC/lFjlPSaVuOrLz8+7POwzzuRg3phNHCSo4YuUnruUYMQammuxZo6sTpNvdfrNTvcIE2NUkxc28Zd2msgNI69z4PwjTPg8dDp8nfdSz5wLsKuk8iKL5Nk+PnBwc3NTSurqhVG/YN+v9Max24DQTOD+KiRnnwOxS1kuqEyOdE0fPCX9oUqvukFceIEXd5Aogsj78uPPzq88QI3vEE3nptcHjVMXW+gS+71L6FPpmE10IFINARAhrybeNc8hqxzl7LPyWDYkMmcQDz/SJ0hf9qdBnK9a8/l0VFDazHbME0d25TpFrVM3EBh5PEgSdPitM6DrLTDa4/fqGLFmawRWpmEod9xRInop58Q0YiGnokDVgcCB8NQjzR1T6PqQNRBVwem0ugqu66S6iqNrtLotIGuvdjr+Pyo0XP8GBD0gl4E7E2v42Tic9me9Mas9/gZ9Cn2biEx1UBMFORwX9OeiT8D/nTx4GCxk3iu1iQa1aw0q9KkRvUqyVYdpVmduhCj5ToJK+mmsaJS1e8q/cRsDlqoSv6Tf7ka6apuLteorrer0NDvpYuHB5mqHKbageJLkTaVnoQPYqEv1EbMFmKPEQPdMEyQcoawDQeTINAGhBnSGVxiCxniaCJqwgMdUWQhkQ5TJJWDWfCfbsrCDMSgMHHXBJ1EGCrSEaMIS53SEWgSknoJOkoopGAMMcgkqsdEFEENpBtwRS2kQxuFSpoYElLICNdQPUEUIyoyYxMRAxmiPKwLVTcs0XQokiBDQwYWBYJWg0YrbYb0FqKiN0YKlxcMR8kCRN2Bm50m4XDKBaQGezSzeso+LRjFjw59p8N98BPvBJMIXTu+0AhZUS8MEpSRSNS9fuQML71u/I4nCeSK0Qfn2rlwEj4+g9RxVrdM2w2D+JsoTE5DfzQIYoS6oa9N2xz6eO6cTFsNF3TugT7/gM09MObOzcJ6Q3iCRjGH+sMozpI7rnsuUsxMAyD5NvAnJxF3roaht9iNwwPpcg75qOt7rucE34GwiloELmjqgYS5yjyQobGsIWHkvpvEIMFo/FcehWCqTPC58x/IN0kfYday5z9Cg7qOUD7dXnwCHm5S+khWza+nDDljPutsPxKaPXdxHp+E/uyW7P+pM0xGkQweQEcj0avjoO9zKSPS3IJn7l51wvE7JRxUlfV+MuQii2xBpy9xR2AbCGOQID121FGmEU2bptJkGk2m0DJp89zpc2wTmUIeO+ooU4H4qqalXcVZN7GWVePF0qJpjVRvMmslhF84+lHgJRfZReJ1r9KuYpXhzWjQ4VMRWiwT76rMw4MlGTu84lHA/VSkgcxROIqVhs5Ju8u73gAu1YMUEkfQ9WdogLrr8n7Es4b7MjBTgMmn2ry05m7Los6icHAeXL8HWVhqwOFB1srDuBt5QyFzqANu4IrPpMr1Yge8iDufT+ggdL0rvAXAkwhoTiKn329+y3s+vxL3QVtHyWUI5H/jJBFAiN5AGwdOEIBmXI784eUk9q5uvCuv5YpqwA4B2EJbfT6A4AwlUiKlUE+ZeSOjPkEBCjsfwBQuUzcHLiQolE8pyQ7U74jYMEXKdyY8WqBBFtgO3WVEgTDZbbAMQyUQQ86VLKkWw8kQipMquGDZoPsxGosY3wLvPDlqNI2WCFtuVdiv4l7RXaGZC9Zc3V2iF2ROIZXDLBgNOCA+BcWXqEHOUZqftFIlXkAyjTtUnpm2zOM4tQaanur6DEmcQ1IrRDJNF/siPEcDL1DtQQMHsBHUdGJwOgmMUEDug9kIRTUvNdoQ3onxD+Sw5JAJ0GSGPOt5Yz51qSB/3i3on7PQo5nRScAfXkHQH8tQMkltoDx55bkuD6bNXSZe9DdHvVZE/TxP3XAAGuCiQMZh30jZnsUFDnjY8TEYpxT4UZLdPVEFpdnXKMlJXkkWqK2gI9pKDSnmdYca0sw4lSTvQD/W4z4pxP1VHdxfbWicMFFKJY8VDNSdw6+l6JOWiFZ2Dv95kIDzBHwKRR85uIyN0zpsnD6oFuTBbN6fLBfbkOM66B0/fhtC7tSGnHpR1+fHUXcJ+1MlwK/gQFLMF1jgq1mAyMrrDp1oxgTfQcizBRWFvpKs9pUwluLBNTQVhm4IjbV0WnOiZWRkd8Y404sJTm/d4jmmBiJyHKPjLP1xluoYsG1aLcsSccgxTcs91rPijtlcV/mPgepBrIJ4bzD0va6XTLnxhRhNrRKIXT5Sv+J8KIZIb4P3kRPEYhJWpZkbAWytoc/raOjzR6+h9+/ki2F/UQf2F48e9ru1i9VhP6sD+9mjh53uCewv68D+8tHD3tw17quH2u7yUJtm1dUdapdPWWwx0NbSYTatPcw2jWyYrbGHHmYXkl6uG9/JSGRJOZ5oz5D2VAVr4rzpPs2pyvVqVVERzpTG64cN1ApGHDQV+VlZGwRzc1OLafzUhfCUx54TpPKVwLW0P2i+9iV9K6dHBlS+k/Alhl4qcq7zFuwTZxjGX9SyY2mW/RgSTm3SlKHdOoMyRI/LED2uj+jxfiFKHgbRkzJET+ojerJfiOKHQfS0DNHT+oie7hWiObN8P4A+LwP0eX1An+8VoA8koS/KAH1RH9AXewXoAxnRszJAz+oDerZXgN6xny8a9PEciud18DvfBjnMaAXs7nx9FYIBE5s20bBh67pJxGa6icCeELinGdiyCCY6vgNGvnUmxf7sPEeLs5qWCErKQHc2I2XVYu02cUEOxkkx5mtHHmzNNPLDzttuGqH8gDeIUSDTZqNHsdGvrw4ddXi0kcp5GbDn9f3AeZkfuP8V2bWGCVTKNE3bsqmFsWmZzL4fyzSVPGWhZiAv2qkq4C9Yq21c8B7YrKbVAkdmGhrTLKpjk1iP1oS1vSjKzXydrlxiT4WCbGLDyB7asLuZbi8E9nwVsOebOIfzLZ3DHdmxavGVZt6rGSMLZuwHXGbI1jFQYMqK8C8zZt0wcD0VwIq9yWnqgTPG6Ld//Rtp6Ld//kfMwZPFS6outzWIeEODKLiaFBL7yIO4Ygu46PmKFfbrOor69R5ZPojaDJPaukZtU9eJxmz9RVN85eXuIrpic5jGAeuN4sbh3T4GeVVjPHov1vHrBau4OsTbMNCrG+79viwkkTT+fkLGt1FyGfbDwPEvoPHFoaNTIked1bIj0JgKRGdfVktL9bVotqi51VLqKmp3wkgJL70avPT2hZf86IwUM5PGmQ/ATNlGZmfe83VydLyu4+le30dksXJKdo4Su2Ub1LawTXQG6JvpMJq0sIGJqWGd6IZOLZbaRLE9c/ZtObJDR7cG+Xn8ezn8L+rgf7FHkd0S/IZdjL9dCD/dIfzveF/cL7ZFr3OA91cDHqelZYj292T1hrR0mzFiYGzppkYtMnUNWBggG55iYhBs0Sq+YbrxCe+l319J6UWO0st6lF7uK6XpzMUSoRUcyqOk87Wi87QkTujWI7W73RTvTrdWMA1iBGpZmBHbwKZZzKtSVNqiBoTqlm5BzG4ZjNFHG62XaO28/8vrrlePZu/uaa4afyzzbOEV+rtMM2WPiGY+HkbQMDFKznYWxw0Ed4FQHvSTy791v0efofTc+169MWLN3uQ4/z1g3dAgaNAM3YQ4mlG9ug3G65ssxvRpo6NwFLhPKPoUPfFRE7nx06foANEqzZalLDV8KkQbtbTqmn3pVPKH6pMkH/bE8+1yync6mCJ7oi0V1wiqzIVdVaf26lFSW2eqas+JLtr/5OQYbdcZ7rXvaTL57jdB6S1m6pgyS7OIzXTTZqlQaMxglhhEWiaEwCa7g3nowm9ctMt2Qo1WE7T0NYvRfWwsqBiQ4JbFIN5gBkQkOowPDTP7qjfoFjNNYEBjzLQNY/uFtDrfw5Aut72ao7JdOKOyXTijKusDy2Td316QPzBl7TLK2vVX1tr3uqZWNfAvMWbAmq2DF8OWZsIQwDbI/VmzgpAih/9NLWW5+b+aVFSTebHe/RadWnufZpn2SmMecItOIfDt9ZsB2ptuBmg/wGaAijRUtVt3sRmgmIcKDNTbozbL9BiQz4W/9+UvZnZCEtAunVu4reUzbh/Lvovt/E7O7egP4HaW/MMm9M9bwZy9WxCDQS0xGPxBxYA8nBhUiUGKp+ffKP7foM/QEzeWryFYZt+N1wQhy5P0IsNW0eMOp+lnr49bnF1OX3XJWpbOMNVs07CppjN9c+4eeP7pbBTIQpf4jb3gCUGfol//Lqa7x6iJxk/eyPlu/ylwPoELJQFjdUbUGTwSufz8KIL7/prXhvWylkzHEjLPQ48n6nO6dkGB5BcUJGr1FxVIfjXEWPyw6pO31RpP842nmzWeLjee7XBFRL4wumTpWMlr2QryL/9dLafyhcTTfkDqpV5oLZ0QRjFjVLeEjbBT67DDb6QStgMhXrOfzIm6syhSz6Z1fT+8kS9IHkuEq5qZIjoWVjRSUvIrvb/8XIuOn9fSYdH/01FEx/kCES9zRPz6jzpEQOrVROB1LKx6pdQGJLzt9WKeqJm4dM/ZnlGUN7fv+TjJVp8/+XEUJl+0nbE3GA0QBAMQEKC3kRuMgv6f1MNG3uwmUEJjsbidRdnVbXVNlxtDH2QocCyw424u3pG/DBGDP+nNfkVB/hKA1sjCqEy8Fl/shFt2ugNXb2FS9m6nYiJIIRG3N9zbjIkawW4pE+RRMzH/OxSYznhZuF/tBVwVNhGd5ixaUG98Emy/Vr6rtYTlFwJW3Oe3JyOQg/nfXhDX2a91ffk/UEsHCPpmJxxADgAASmwAAFBLAQIUABQACAgIAAtpPkLWN725GQAAABcAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAICAgAC2k+QvpmJxxADgAASmwAAAwAAAAAAAAAAAAAAAAAXQAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAADXDgAAAAA=" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />
  

Version vom 30. Januar 2013, 13:14 Uhr

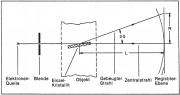
Elektronenbeugung Debey-Scherrer-Verfahren

Aufbau
Versuchsaufbau Elektronenbeugung


Beobachtung
Erklärung

Animation: Braggsche Reflektionsbedingung

Dargestellt sind zwei Atomebenen im Abstand d.

Bitte installiere Java, um diese Seite nutzen zu können.
Interferenzbedingungen


Links

Von „http://schulphysikwiki.de/index.php?title=Materiewellen_nach_de_Broglie&oldid=5596“