Materiewellen nach de Broglie: Unterschied zwischen den Versionen

Aus Schulphysikwiki
Wechseln zu: Navigation, Suche
(→‎Animation: Braggsche Reflektionsbedingung)
(→‎Animation: Braggsche Reflektionsbedingung)
Zeile 8: Zeile 8:
 
====Animation: Braggsche Reflektionsbedingung====
 
====Animation: Braggsche Reflektionsbedingung====
 
Dargestellt sind zwei Atomebenen im Abstand d.  
 
Dargestellt sind zwei Atomebenen im Abstand d.  
−
<ggb_applet width="736" height="633"  version="4.0" ggbBase64="UEsDBBQACAgIAAtpPkIAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIAAtpPkIAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7V3bctvGGb5OnmLLi4ydmBR2F4tDIiUjyZatWLQzsZvptJPJgMSSggUCDABKpCYXveq0T9HbXjfvkbxDnqT/7gI8ASABkpKopBzLOO3x+/7THggefjUe+OiaR7EXBkcN3NIaiAfd0PWC/lFjlPSaVuOrLz8+7POwzzuRg3phNHCSo4YuUnruUYMQammuxZo6sTpNvdfrNTvcIE2NUkxc28Zd2msgNI69z4PwjTPg8dDp8nfdSz5wLsKuk8iKL5Nk+PnBwc3NTSurqhVG/YN+v9Max24DQTOD+KiRnnwOxS1kuqEyOdE0fPCX9oUqvukFceIEXd5Aogsj78uPPzq88QI3vEE3nptcHjVMXW+gS+71L6FPpmE10IFINARAhrybeNc8hqxzl7LPyWDYkMmcQDz/SJ0hf9qdBnK9a8/l0VFDazHbME0d25TpFrVM3EBh5PEgSdPitM6DrLTDa4/fqGLFmawRWpmEod9xRInop58Q0YiGnokDVgcCB8NQjzR1T6PqQNRBVwem0ugqu66S6iqNrtLotIGuvdjr+Pyo0XP8GBD0gl4E7E2v42Tic9me9Mas9/gZ9Cn2biEx1UBMFORwX9OeiT8D/nTx4GCxk3iu1iQa1aw0q9KkRvUqyVYdpVmduhCj5ToJK+mmsaJS1e8q/cRsDlqoSv6Tf7ka6apuLteorrer0NDvpYuHB5mqHKbageJLkTaVnoQPYqEv1EbMFmKPEQPdMEyQcoawDQeTINAGhBnSGVxiCxniaCJqwgMdUWQhkQ5TJJWDWfCfbsrCDMSgMHHXBJ1EGCrSEaMIS53SEWgSknoJOkoopGAMMcgkqsdEFEENpBtwRS2kQxuFSpoYElLICNdQPUEUIyoyYxMRAxmiPKwLVTcs0XQokiBDQwYWBYJWg0YrbYb0FqKiN0YKlxcMR8kCRN2Bm50m4XDKBaQGezSzeso+LRjFjw59p8N98BPvBJMIXTu+0AhZUS8MEpSRSNS9fuQML71u/I4nCeSK0Qfn2rlwEj4+g9RxVrdM2w2D+JsoTE5DfzQIYoS6oa9N2xz6eO6cTFsNF3TugT7/gM09MObOzcJ6Q3iCRjGH+sMozpI7rnsuUsxMAyD5NvAnJxF3roaht9iNwwPpcg75qOt7rucE34GwiloELmjqgYS5yjyQobGsIWHkvpvEIMFo/FcehWCqTPC58x/IN0kfYday5z9Cg7qOUD7dXnwCHm5S+khWza+nDDljPutsPxKaPXdxHp+E/uyW7P+pM0xGkQweQEcj0avjoO9zKSPS3IJn7l51wvE7JRxUlfV+MuQii2xBpy9xR2AbCGOQID121FGmEU2bptJkGk2m0DJp89zpc2wTmUIeO+ooU4H4qqalXcVZN7GWVePF0qJpjVRvMmslhF84+lHgJRfZReJ1r9KuYpXhzWjQ4VMRWiwT76rMw4MlGTu84lHA/VSkgcxROIqVhs5Ju8u73gAu1YMUEkfQ9WdogLrr8n7Es4b7MjBTgMmn2ry05m7Los6icHAeXL8HWVhqwOFB1srDuBt5QyFzqANu4IrPpMr1Yge8iDufT+ggdL0rvAXAkwhoTiKn329+y3s+vxL3QVtHyWUI5H/jJBFAiN5AGwdOEIBmXI784eUk9q5uvCuv5YpqwA4B2EJbfT6A4AwlUiKlUE+ZeSOjPkEBCjsfwBQuUzcHLiQolE8pyQ7U74jYMEXKdyY8WqBBFtgO3WVEgTDZbbAMQyUQQ86VLKkWw8kQipMquGDZoPsxGosY3wLvPDlqNI2WCFtuVdiv4l7RXaGZC9Zc3V2iF2ROIZXDLBgNOCA+BcWXqEHOUZqftFIlXkAyjTtUnpm2zOM4tQaanur6DEmcQ1IrRDJNF/siPEcDL1DtQQMHsBHUdGJwOgmMUEDug9kIRTUvNdoQ3onxD+Sw5JAJ0GSGPOt5Yz51qSB/3i3on7PQo5nRScAfXkHQH8tQMkltoDx55bkuD6bNXSZe9DdHvVZE/TxP3XAAGuCiQMZh30jZnsUFDnjY8TEYpxT4UZLdPVEFpdnXKMlJXkkWqK2gI9pKDSnmdYca0sw4lSTvQD/W4z4pxP1VHdxfbWicMFFKJY8VDNSdw6+l6JOWiFZ2Dv95kIDzBHwKRR85uIyN0zpsnD6oFuTBbN6fLBfbkOM66B0/fhtC7tSGnHpR1+fHUXcJ+1MlwK/gQFLMF1jgq1mAyMrrDp1oxgTfQcizBRWFvpKs9pUwluLBNTQVhm4IjbV0WnOiZWRkd8Y404sJTm/d4jmmBiJyHKPjLP1xluoYsG1aLcsSccgxTcs91rPijtlcV/mPgepBrIJ4bzD0va6XTLnxhRhNrRKIXT5Sv+J8KIZIb4P3kRPEYhJWpZkbAWytoc/raOjzR6+h9+/ki2F/UQf2F48e9ru1i9VhP6sD+9mjh53uCewv68D+8tHD3tw17quH2u7yUJtm1dUdapdPWWwx0NbSYTatPcw2jWyYrbGHHmYXkl6uG9/JSGRJOZ5oz5D2VAVr4rzpPs2pyvVqVVERzpTG64cN1ApGHDQV+VlZGwRzc1OLafzUhfCUx54TpPKVwLW0P2i+9iV9K6dHBlS+k/Alhl4qcq7zFuwTZxjGX9SyY2mW/RgSTm3SlKHdOoMyRI/LED2uj+jxfiFKHgbRkzJET+ojerJfiOKHQfS0DNHT+oie7hWiObN8P4A+LwP0eX1An+8VoA8koS/KAH1RH9AXewXoAxnRszJAz+oDerZXgN6xny8a9PEciud18DvfBjnMaAXs7nx9FYIBE5s20bBh67pJxGa6icCeELinGdiyCCY6vgNGvnUmxf7sPEeLs5qWCErKQHc2I2XVYu02cUEOxkkx5mtHHmzNNPLDzttuGqH8gDeIUSDTZqNHsdGvrw4ddXi0kcp5GbDn9f3AeZkfuP8V2bWGCVTKNE3bsqmFsWmZzL4fyzSVPGWhZiAv2qkq4C9Yq21c8B7YrKbVAkdmGhrTLKpjk1iP1oS1vSjKzXydrlxiT4WCbGLDyB7asLuZbi8E9nwVsOebOIfzLZ3DHdmxavGVZt6rGSMLZuwHXGbI1jFQYMqK8C8zZt0wcD0VwIq9yWnqgTPG6Ld//Rtp6Ld//kfMwZPFS6outzWIeEODKLiaFBL7yIO4Ygu46PmKFfbrOor69R5ZPojaDJPaukZtU9eJxmz9RVN85eXuIrpic5jGAeuN4sbh3T4GeVVjPHov1vHrBau4OsTbMNCrG+79viwkkTT+fkLGt1FyGfbDwPEvoPHFoaNTIked1bIj0JgKRGdfVktL9bVotqi51VLqKmp3wkgJL70avPT2hZf86IwUM5PGmQ/ATNlGZmfe83VydLyu4+le30dksXJKdo4Su2Ub1LawTXQG6JvpMJq0sIGJqWGd6IZOLZbaRLE9c/ZtObJDR7cG+Xn8ezn8L+rgf7FHkd0S/IZdjL9dCD/dIfzveF/cL7ZFr3OA91cDHqelZYj292T1hrR0mzFiYGzppkYtMnUNWBggG55iYhBs0Sq+YbrxCe+l319J6UWO0st6lF7uK6XpzMUSoRUcyqOk87Wi87QkTujWI7W73RTvTrdWMA1iBGpZmBHbwKZZzKtSVNqiBoTqlm5BzG4ZjNFHG62XaO28/8vrrlePZu/uaa4afyzzbOEV+rtMM2WPiGY+HkbQMDFKznYWxw0Ed4FQHvSTy791v0efofTc+169MWLN3uQ4/z1g3dAgaNAM3YQ4mlG9ug3G65ssxvRpo6NwFLhPKPoUPfFRE7nx06foANEqzZalLDV8KkQbtbTqmn3pVPKH6pMkH/bE8+1yync6mCJ7oi0V1wiqzIVdVaf26lFSW2eqas+JLtr/5OQYbdcZ7rXvaTL57jdB6S1m6pgyS7OIzXTTZqlQaMxglhhEWiaEwCa7g3nowm9ctMt2Qo1WE7T0NYvRfWwsqBiQ4JbFIN5gBkQkOowPDTP7qjfoFjNNYEBjzLQNY/uFtDrfw5Aut72ao7JdOKOyXTijKusDy2Td316QPzBl7TLK2vVX1tr3uqZWNfAvMWbAmq2DF8OWZsIQwDbI/VmzgpAih/9NLWW5+b+aVFSTebHe/RadWnufZpn2SmMecItOIfDt9ZsB2ptuBmg/wGaAijRUtVt3sRmgmIcKDNTbozbL9BiQz4W/9+UvZnZCEtAunVu4reUzbh/Lvovt/E7O7egP4HaW/MMm9M9bwZy9WxCDQS0xGPxBxYA8nBhUiUGKp+ffKP7foM/QEzeWryFYZt+N1wQhy5P0IsNW0eMOp+lnr49bnF1OX3XJWpbOMNVs07CppjN9c+4eeP7pbBTIQpf4jb3gCUGfol//Lqa7x6iJxk/eyPlu/ylwPoELJQFjdUbUGTwSufz8KIL7/prXhvWylkzHEjLPQ48n6nO6dkGB5BcUJGr1FxVIfjXEWPyw6pO31RpP842nmzWeLjee7XBFRL4wumTpWMlr2QryL/9dLafyhcTTfkDqpV5oLZ0QRjFjVLeEjbBT67DDb6QStgMhXrOfzIm6syhSz6Z1fT+8kS9IHkuEq5qZIjoWVjRSUvIrvb/8XIuOn9fSYdH/01FEx/kCES9zRPz6jzpEQOrVROB1LKx6pdQGJLzt9WKeqJm4dM/ZnlGUN7fv+TjJVp8/+XEUJl+0nbE3GA0QBAMQEKC3kRuMgv6f1MNG3uwmUEJjsbidRdnVbXVNlxtDH2QocCyw424u3pG/DBGDP+nNfkVB/hKA1sjCqEy8Fl/shFt2ugNXb2FS9m6nYiJIIRG3N9zbjIkawW4pE+RRMzH/OxSYznhZuF/tBVwVNhGd5ixaUG98Emy/Vr6rtYTlFwJW3Oe3JyOQg/nfXhDX2a91ffk/UEsHCPpmJxxADgAASmwAAFBLAQIUABQACAgIAAtpPkLWN725GQAAABcAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAICAgAC2k+QvpmJxxADgAASmwAAAwAAAAAAAAAAAAAAAAAXQAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAADXDgAAAAA=" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />
 
  
 +
Nur bei bestimmten Winkeln ist der Gangunterschied ein Vielfaches der Wellenlänge. Für diese Fälle liegt konstruktive Interferenz vor.
 +
 +
<ggb_applet width="736" height="619"  version="4.0" ggbBase64="UEsDBBQACAgIAEa1PkIAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgICABGtT5CAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbO1dyXLbRho+J0/Rw0PKTkwK3Y3GkkhJSbJlK5bsVOxJTc1UKgUSTQoWCDAAKJGqHOY0NfMUc51zcvQ7OO+QJ5m/uwFuAEiApCQqCcsytl6/7996Ibj/1ajvoysexV4YHDRwS2sgHnRC1wt6B41h0m1aja++/Hi/x8Meb0cO6oZR30kOGrpI6bkHDUKopbkWa+rEajf1brfbbHODNDVKMXFtG3dot4HQKPY+D8JXTp/HA6fD33QueN85CztOIiu+SJLB53t719fXrayqVhj19nq9dmsUuw0EzQzig0Z68jkUN5fpmsrkRNPw3t/Oz1TxTS+IEyfo8AYSXRh6X3780f61F7jhNbr23OTioGHqegNdcK93AX0yDauB9kSiAQAy4J3Eu+IxZJ25lH1O+oOGTOYE4vlH6gz5k+40kOtdeS6PDhpai9mGaerYpky3qGXiBgojjwdJmhande5lpe1fefxaFSvOZI3QyiQM/bYjSkQ//YSIRjT0RBywOhA4GIZ6pKl7GlUHog66OjCVRlfZdZVUV2l0lUanDXTlxV7b5weNruPHgKAXdCNgb3IdJ2Ofy/akN6a9x0+gT7F3A4mpBmKiIIf7mvZE/Bnwp4sHe/OdxDO1JtGwZqVZlSYxqldJNuoozerUhRgt1klYSTeNJZWqflfpJ2Yz0EJV8p/8y9VIl3VzsUZ1vVmFhn4nXdzfy1RlP9UOFF+ItKn0JLwfC32hNmK2EHuMGOiGYYKUM4RtOJgEgTYgzJDO4BJbyBBHE1ETHuiIIguJdJgiqRzMgv90UxZmIAaFibsm6CTCUJGOGEVY6pSOQJOQ1EvQUUIhBWOIQSZRPSaiCGog3YAraiEd2ihU0sSQkEJGuIbqCaIYUZEZm4gYyBDlYV2oumGJpkORBBkaMrAoELQaNFppM6S3EBW9MVK4vGAwTOYg6vTd7DQJBxMuIDXYo6nVU/Zpzih+tO87be6Dn3gjmEToyvGFRsiKumGQoIxEou71Imdw4XXiNzxJIFeM3jlXzpmT8NEJpI6zumXaThjE30Rhchz6w34QI9QJfW3S5tDHM+dk0mq4oDMP9NkHbOaBMXNuFtYbwhM0jDnUH0Zxltxx3VORYmoaAMnXgT8+irhzOQi9+W7s70mXs8+HHd9zPSf4DoRV1CJwQRMPJMxV5oGYjbOGhJH7ZhyDBKPR33kUgqkywefOfiDfOH2EWcue/YD6xR1HKJ9uzz8BDzcue2SouvnVhCJnxKe97UVCtWcuTuOj0J/ekgAcO4NkGMnoAZQ0Et06DHo+l0Ii7S245s5lOxy9UdJBVVlvxwMussgWtHsSeATGgTAGCdJjWx1lGtG0SSpNptFkCi0TN8+dPMc2kSnksa2OMhXIr2pa2lWcdRNrWTVeLE2a1kgVJzNXQvqFpx8GXnKWXSRe5zLtKlYZXg37bT6Rofky8bbK3N9bELL9Sx4F3E9lGsgchsNYqeiMuLu84/XhUj1IIXEEXX+FBqi7Lu9FPGu4LyMzBZh8qs2Ka+62LOokCvunwdVbkIWFBuzvZa3cjzuRNxAyh9rgBy75VKpcL3bAjbiz+YQSQtc7wl0APImA5ihyer3mt7zr80txH9R1mFyEQP43ThIBhOgVtLHvBAGoxsXQH1yMY+/y2rv0Wq6oBgwRgC3U1ed9iM5QIiVSCvWEmVcy7BMUoLD9DmzhInUz4EKCQvmUkuxA/Y4IDlOkfGfMozkaZIHnobuIKBAmuw2mYaAEYsC5kiXVYjgZQHFSBedMG3Q/RiMR5FtgH8YHjabREnHLjYr7VeAruis0c86cq7sL9ILMKaRymAXDPgfEJ6B8eC9hg6zDtADSSrV4Dso08lCZpuoyC+TEHGh6quxTKHEOSq0QyjRd7IsAHfW9QLUH9R0AR3DTjsHtJDBGAcEPpmMU1bzUbEOAJ0ZAkMOSgyaAkxnyrOuN+MSpggB6N6CAzlyPplYnAY94CWF/LIPJJDWC8uSF57o8mDR3kXnR3xz3WhH3s0R1wj6ogIsCGYl9I4V7Ghk44GNHh2CdUuCHSXb3SBWUZl+hJUd5LZmjtoKSaEtVpJjXLapIM+NUkrwFBVmN+7gQ9xd1cH+xpnXCRCmVPFawULcOv5aiT1oiXtk6/KdBAt4T8CkUfeTgMjaO67BxfK9akAezeXeyXGxDDuugd/jwbQi5VRty7EUdnx9GnQXsj5UAv4ADSTGfY4EvZwFCK68zcKIpE3wLMc8GVBT6SrLcV8JoigdX0FQYvCE00tKJzbGWkZHdGeFML8Y4vXWDZ5jqi9BxhA6z9IdZqkPAtmm1LEvEIYc0LfdQz4o7ZDNd5T8GqgexiuK9/sD3Ol4y4cYXYjSxSiB2+VD9kvOBGCO9Dt5GThCLaViVZmYIsLGGPq2joU8fvIbevZMvhv1ZHdifPXjYb9cuVof9pA7sJw8edrojsD+vA/vzBw97c9u4Lx9ru4tDbZpVV3eoXT5nscFAW0uH2bT2MNs0smG2xu57mF1IerlufCcjkQXleKQ9QdpjFayJ86b7OKcqV8tVRUU4Exqv7jdQKxhx0FTkp2WtEczNzC2m8VMHwlMee06QylcC19L+oNnaF/StnB4ZUPlOwhcYeq7IucpbsE+cQRh/UcuOpVl2Y0g4sUkThrbrDMoQPSxD9LA+ooe7hSi5H0SPyhA9qo/o0W4hiu8H0eMyRI/rI3q8U4jmzPLdAPq0DNCn9QF9ulOA3pOEPisD9Fl9QJ/tFKD3ZERPygA9qQ/oyU4Best+vmjQx3MontbB73QT5DCjFbC79QVWCAZMbNpEw4at6yYR2+nGAntC4J5mYMsimOj4Fhj51hkX+7PTHC3OcloiKCkD3VmPlGWLtZvEBTkYx8WYrxx5sBXTyPc7b7tuhPIDXiNGgUzrjR7FVr+eOrTV4cFGKqdlwJ7W9wOnZX7g7ldkVxomUCnTNG3LphbGpmUy+24s00TylIWagjxvp6qAP2etNnHBO2CzmlYLHJlpaEyzqI5NYj1YE3buRVFu5ut46RJ7KhRkHRtGdtCG3c50eyGwp8uAPV3HOZxu6BxuyY5Vi680807NGJkzYz/gMkO2ioECU1aEf5kx64SB66kAVuxOTlP3nRFGv/3nv0hDv/37f2IOnsxfUnW5qUHEaxpEwdW4kNgHHsQVW8B5z1essF/XUdSvd8jyQdRmmNTWNWqbuk40ZuvPmuJLL7cX0RWbwzQOWG0U1w7vdjHIqxrj0Tuxjl/PWcXlId6agV7dcO/3ZSGJpPH3EzK+jpKLsBcGjn8GjS8OHZ0SOWovlx2BxkQg2ruyWlqqr0WzRc2NllKXUbsVRkp46dbgpbsrvORHZ6SYmTTOvAdmyjYyO7Oer52j42UdT/fyLiKLpVOyM5TYLdugtoVtojNA30yH0aSFDUxMDetEN3RqsdQmiu2Z0+/LkS06uhXIz+LfzeF/Vgf/sx2K7BbgN+xi/O1C+OkW4X/De+J+sS16mQO8txzwOC0tQ7S3I6s3pKXbjBEDY0s3NWqRiWvAwgDZ8BQTg2CLVvENk41PeCf9/lJKz3KUXtSj9GJXKU1nLhYIreBQHiSdLxWdxyVxQqceqZ3Npni3urWCaRAjUMvCjNgGNs1iXpWi0hY1IFS3dAtidstgjD7YaL1Ea2f9X153vXo0e7dPc9X4Y5FnCy/R30WaKXtANPPRIIKGiVFytrM4biC4C4TyoJdc/KPzPfoMpefe9+qdESv2Jsf57wHrhgZBg2boJsTRjOrVbTBe3WQxpk8bHYXDwH1E0afo0Yf3qInc+PFjtIdolXbLYhZaPpGitZpaddG+dC75XfVZknc74vq2Oec7GU2RHVGXiosEVSbDLqtTe/kgqa0zV7XjRBdtgHJyjJ7XGe+d39Fs8u3vgtJbzNQxZZZmEZvpps1SodCYwSwxirRMiIFNdgsT0YVfuTgv2wo1XE7Qwvcshnexs6BiRIJbFoOAgxkQkugwQDTM7LveoFvMNIEBjTHTNozNV9LqfBFD+tzz5RyVbcMZlm3DGVZZIFgk6+42g/yBKTsvo+y8/tLa+Z0uqlWN/EuMGbBm6+DFsKWZMAawDXJ31qwgpMjhf11LWa7/VJOKajIr1tvfo1Nr89M0005pzD3u0SkE/nz1boDzdXcDnN/DboCKNFS1W7exG6CYhwoM1NukNs30EJDPhb935S+mdkIScF46t3BTy2fcPJSNF5v5nZzb0e/B7Sz4h3Xon7WCOXs3Jwb9WmLQ/4OKAbk/MagSgxTPz79S/L9Cn6FHbizfQ7DIvhuvCEIWZ+lFho2ixy3O00/fHzc/vZy+7JK1LJ1hqtmmYVNNZ/r63N3z/NPJMJCFLvAbe8Ejgj5Fv/5TzHePUBONHr2S890f3j8G0sdwpURgpM6IOoNHItuH9/lxBPf9FW8O62ZtmYwmZJ77HlHUZ3XlmgLJryko2OqvK5D8iogx/2HV52+rtZ7mW0/XbD1dbD3b4qqIfG10yfqxEtmyZeQPPy+XVPla4unbaX/Or+3ohDCKGaO6JeyEnVqILX4tlbAtiPGKTWVO1JlGkno2tev74bV8TfJIIlzV1BTRMbeqkZKSX+798EstOn5ZSYdF/6SjiI7TOSKe54j49V91iIDUy4nAq1hY9l6pNUh43e3GPFGzcenGsx2jKG9v3/JRki1Bf/LjMEy+OHdGXn/YRxAQQFCAXkduMAx6f1EPG3mzm0AJjfnithZpV7fVNZ1uDH2QwcChwI67uZhH/kBEDP6kO/0xBfl7AFojC6Uy8Zp/uxNu2ek2XL2FSdkLnoqJIIVE3Fxzbz0magS8pUyQB83E7M9RYDrlZe5+tbdwVdhJdJyzaEG9MUqw+Xr5ttYTFt8KWHGz346MQvZmf4FBXGc/2vXl/wFQSwcIhPB11UoOAABRbAAAUEsBAhQAFAAICAgARrU+QkXM3l0aAAAAGAAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgICABGtT5ChPB11UoOAABRbAAADAAAAAAAAAAAAAAAAABeAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAOIOAAAAAA==" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "false" />
 
<br style="clear: both" />  
 
<br style="clear: both" />  
  

Version vom 30. Januar 2013, 22:56 Uhr

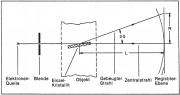
Elektronenbeugung Debey-Scherrer-Verfahren

Aufbau
Versuchsaufbau Elektronenbeugung


Beobachtung
Erklärung

Animation: Braggsche Reflektionsbedingung

Dargestellt sind zwei Atomebenen im Abstand d.

Nur bei bestimmten Winkeln ist der Gangunterschied ein Vielfaches der Wellenlänge. Für diese Fälle liegt konstruktive Interferenz vor.

Bitte installiere Java, um diese Seite nutzen zu können.
Interferenzbedingungen


Animation: Maxima des Debey-Scherrer-Verfahrens / Pulver-Verfahrens

Dargestellt ist einer der vielen kleinen Kristalle des Pulvers. Der Kristall kann in seiner Lage durch die Angabe des Winkels [math]\varphi[/math] verändert werden.

Für manche Winkel ist die Braggsche Interferenzbedingung für das erste, zweite, usw. Maxima erfüllt. Im Pulver sind die kleinen Kristalle in allen möglichen Lagen vorhanden, weswegen es auch für alle Winkel Kristalle gibt, welche die Interferenzbedingung erfüllen.

Trifft der Elektronenstrahl auf den fluoreszierenden Schirm, so sieht man dort einen Fleck.

Bitte installiere Java, um diese Seite nutzen zu können.

Links

Von „http://schulphysikwiki.de/index.php?title=Materiewellen_nach_de_Broglie&oldid=5600“