Ortsdiagramme von Bewegungen: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „===Versuch: Ortsdiagramm mit Ultraschallsensor=== ;Aufbau Ein Ultraschallsensor sendet für den Menschen nicht hörbare kurze Schallsignale aus. Werden diese an e…“) |
K (→Versuch: Ortsdiagramm mit Ultraschallsensor) |
||
| Zeile 9: | Zeile 9: | ||
;Messungen | ;Messungen | ||
| + | |||
| + | Hier sollen Bilder von Ergebnissen hin. | ||
;Auswertung | ;Auswertung | ||
| Zeile 21: | Zeile 23: | ||
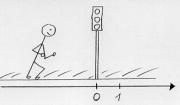
[[Image:Mechanik_Koordinatensystem_geradlinig.jpg|thumb|Die Ampel dient als Koordinatenursprung]] | [[Image:Mechanik_Koordinatensystem_geradlinig.jpg|thumb|Die Ampel dient als Koordinatenursprung]] | ||
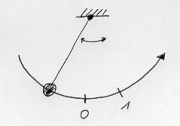
| − | [[Image:Mechanik_Koordinatensystem_gebogen.jpg|thumb|Gebogenes Koordinatensystem für ein Fadenpendel]] | + | [[Image:Mechanik_Koordinatensystem_gebogen.jpg|thumb|Gebogenes Koordinatensystem für ein Fadenpendel]] |
| + | |||
== Wann ist der Gegenstand wo? == | == Wann ist der Gegenstand wo? == | ||
Zur genaueren Beschreibung einer Bewegung muss man ein Orts-Koordinatensystem festlegen. Dies kann geradlinig oder auch gebogen sein, wie im Falle eines Fadenpendels. Bei vielen Fällen reicht ein eindimensionales Koordinatensystem, bei dem sich der Körper nur nach vorne und hinten bewegen kann, aus. Mit einem negativen Vorzeichen wird eine Position vor dem Ursprung angegeben. | Zur genaueren Beschreibung einer Bewegung muss man ein Orts-Koordinatensystem festlegen. Dies kann geradlinig oder auch gebogen sein, wie im Falle eines Fadenpendels. Bei vielen Fällen reicht ein eindimensionales Koordinatensystem, bei dem sich der Körper nur nach vorne und hinten bewegen kann, aus. Mit einem negativen Vorzeichen wird eine Position vor dem Ursprung angegeben. | ||
Version vom 18. September 2014, 01:03 Uhr
Versuch: Ortsdiagramm mit Ultraschallsensor
- Aufbau
Ein Ultraschallsensor sendet für den Menschen nicht hörbare kurze Schallsignale aus. Werden diese an einem Gegenstand reflektiert, so kann der Sensor das Echo wieder registrieren. Aus der gemessenen Zeitdauer und der bekannten Schallgeschwindigkeit kann man daraus die Entfernung zwischen Sensor und Gegenstand berechnen.
Mit Hilfe des Sensors kann von einer Software 25 mal in der Sekunde die Position eines Gegenstandes bestimmt werden. Diese Werte werden in eine Tabelle geschrieben und über der Zeit als Diagramm aufgetragen.
- a) Eine Person läuft
- b) Ein Federpendel schwingt
- c) Ein Fadenpendel schwingt
- Messungen
Hier sollen Bilder von Ergebnissen hin.
- Auswertung
Aus dem Ortsdiagramm kann man ablesen wann die Person wo war, wie weit sie gelaufen ist, wann sie steht und wann sie läuft, in welche Richtung sie läuft und wie schnell sie läuft.
- Beschreibung einer Bewegung als "Geschichte".
- Berechnung von positiven und negativen Durchschnittsgeschwindigkeiten
- Berechnung einer Momentangeschwindigkeit
Wann ist der Gegenstand wo?
Zur genaueren Beschreibung einer Bewegung muss man ein Orts-Koordinatensystem festlegen. Dies kann geradlinig oder auch gebogen sein, wie im Falle eines Fadenpendels. Bei vielen Fällen reicht ein eindimensionales Koordinatensystem, bei dem sich der Körper nur nach vorne und hinten bewegen kann, aus. Mit einem negativen Vorzeichen wird eine Position vor dem Ursprung angegeben.
Das Koordinatensystem kann aber auch zwei- oder dreidimensional sein. Bei Bewegungen in der Fläche oder im Raum ist der Ort eine vektorielle Größe, die man als [math]\vec s[/math] notiert.
In diesem Koordinatensystem kann man nun die Position eines festen Punktes des Körpers, häufig des Schwerpunkts S, mit Hilfe von Koordinaten exakt angeben.
Ordnet man jedem Zeitpunkt einem Ort zu, so erhält man das Ortsgesetz [math]s(t)[/math] der Bewegung. Das Schaubild dieser Zuordnung ist das Ort-Zeit-Diagramm.
- Die Steigung einer Tangente des Schaubildes ist die Momentangeschwindigkeit [math]v=\dot s[/math] des Körpers,
- die Sekantensteigung ist die mittlere Geschwindigkeit [math]\bar v = \frac{\Delta s}{\Delta t}[/math].