Reflektion und Brechung einer Welle: Unterschied zwischen den Versionen

Version vom 27. November 2014, 12:27 Uhr

(Kursstufe > Mechanische Wellen)

Versuch: Über eine Geschwindigkeitsgrenze laufen

Aufbau

Auf dem Rasen laufen wir langsamer als auf dem Asphalt. Wir bilden eine Kette und laufen schräg über die Grenze zwischen Rasen und Asphalt. Dabei soll die Kette immer senkrecht zur Bewegungsrichtung bleiben.

(Weil es an diesem Tag geschneit hat, haben wir das Drinnen simuliert :)

Beobachtung

Wenn wir die Grenze überschreiten, macht die Menschenkette einen Knick. Nach dem Überschreiten hat die Kette eine andere Richtung als vorher.

Das sieht man einigermaßen auf diesen Videos:

Video: Übergang von großer zu kleiner Geschwindigkeit

Video: Übergang von kleiner zu großer Geschwindigkeit

Wie man gut erkennt, ist es für die laufenden Personen zwar klar, wie schnell sie nach Überschreiten der Grenze laufen sollen, aber nicht in welche Richtung.

Ergebnis

An einer Geschwindigkeitsgrenze ändert sich die Ausbreitungsrichtung einer Menschenkette. Kann man das auf die Ausbreitung einer Welle übertragen?

Versuch: Geschwindigkeitsgrenzen in der Wellenwanne

Aufbau

Die Wasserwellen in der Wanne sind eine Mischung aus Schwerewellen und Kapillarwellen. Die Ausbreitungsgeschwindigkeit der Schwerewellen hängt von der Wassertiefe ab. Durch in die Wanne gelegte Kunststoffplatten kann man gezielt an manchen Orten die Phasengeschwindigkeit verkleinern. Da die Kappillarwellen nun stören, kann man sie durch die Hinzugabe von Spülmittel reduzieren. Denn so verkleinert sich die Oberflächenspannung.

Eine Sammellinse

Eine ebene Welle trifft auf ein konvex geformtes Gebiet niedriger Wassertiefe.

Eine Zersteuungslinse

Eine ebene Welle trifft auf ein konkav geformtes Gebiet niedrigerer Wassertiefe.

Eine planparallele Platte

Die ebene Welle trifft auf einen parallelen Streifen mit niedrigerer Wassertiefe.

Beobachtung

Am besten Fotos....

Bei der Sammellinse passiert tatsächlich das, was der Name ja schon sagt: Die ebene Welle wird zweimal gebrochen, nämlich beim Eintritt und beim Austritt der Linse. Dadurch läuft sie hinter der Linse auf einen Punkt, den Brennpunkt der Linse, zu.

Bei der Zerstreuungslinse ist der gegenteilige Effekt zu beobachten. Nach der zweimaligne Brechung läuft die Welle auseinander.

Bei der planparallelen Platte erkennt man, wie die Welle im Bereich der Platte eine andere Ausbreitungsrichtung hat und danach wieder die ursprüngliche.

• 

  Video (Youtube "Refraction - Refracción" von "razzmatazz1974")

• 
• 

Ergebnisse

Eine Welle ändert an der Grenze zweier Gebiete mit unterschiedlicher Phasengeschwindigkeit ihre Richtung.

Beim Übergang von der geringen zur großen Geschwindigkeit bricht die Welle vom Lot weg. (Umgekehrt zum Lot hin.)

Die Wasserwellen verhalten sich so, wie man das aus der Optik von der Ausbreitung des Lichtes her kennt! Demnach kann man die Lichtbrechung durch die unterschiedliche Phasengeschwindigkeit von Licht in verschiedenen Medien erklären.

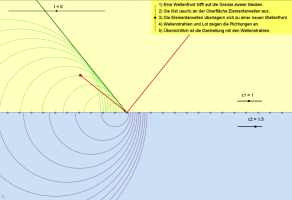
Erklärung der Brechung mit dem Huygensschen Prinzip

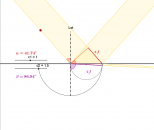
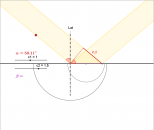
Animation: Brechung einer Welle

Animation: Konstruktion der gebrochenen Welle nach Huygens

An dem roten Punkt läßt sich der Einfallswinkel verändern.

Mit den Schiebereglern lassen sich die Phasengeschwindigkeiten der Welle in den zwei Medien verändern.

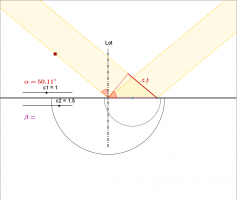
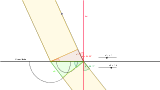
Totalreflektion

Vergrößert sich bei einem Übergang in ein anderes Medium die Ausbreitungsgeschwindigkeit der Welle, so stellt man fest, dass die Welle unter Umständen gar nicht in das neue Medium hineingeht, sondern ausschließlich reflektiert wird.

Mit dem Huygenschen Prinzip läßt sich das erklären: Trifft die Welle mit einem relativ großen Einfallswinkel auf die Grenzfläche, so interferieren die an der Grenzfläche ausgelösten Elementarwellen nicht mehr zu einer Wellenfront.

Diese Totalreflektion beobachtet man bei Licht beim Übergang von Wasser oder Glas in Luft.

• 

  Die Elementarwellen sind "zu schnell".

• 

  Grenzwinkel der Totalreflektion

• 

  Totalreflektion

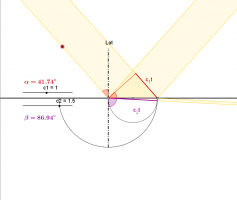
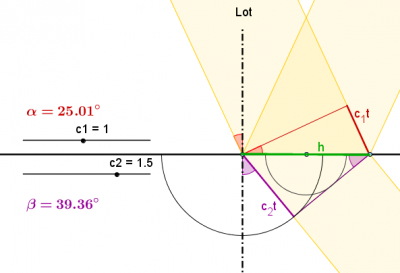
Das Brechungsgesetz

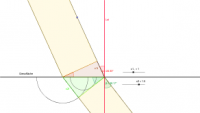
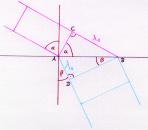
Zwischen dem Einfallswinkel [math]\alpha[/math], dem Brechungswinkel [math]\beta[/math] und den Phasengeschwindigkeiten muss es einen Zusammenhang geben. Denn bei der Konstruktion der Brechung nach Huygens reicht die Angabe von [math]\alpha[/math] und den beiden Geschwindigkeiten aus, der Brechungswinkel [math]\beta[/math] liegt dann fest.

In der Konstruktionszeichnung treten zwei rechtwinklige Dreiecke auf. Die gemeinsame Hypothenuse soll [math]h[/math] heißen.

In diesen Dreiecken tauchen jeweils der Einfalls- bzw. Brechungswinkel auf.

Für den Sinus im oberen und unteren Dreieck folgt:

[math]\left. \begin{matrix}\sin(\alpha) = \frac{c_1 \, t}{h} \quad |: c_1 \, t \\ \sin(\beta) = \frac{c_2 \, t}{h} \quad |: c_2 \, t \end{matrix} \right\} \Longrightarrow \left. \frac{\sin(\alpha)}{c_1 \, t} = \frac{1}{h} = \frac{\sin(\beta)}{c_2 \, t} \right|\cdot \,t [/math]

Mit Brechungsindex

Häufig findet man das Brechungsgesetz für Licht mit Angabe der sogenannten Brechungsindizes [math]n_1[/math] und [math]n_2[/math]. Ist [math]c[/math] die Lichtgeschwindigkeit im Vakuum, so legt man fest:

[math]n_1 = \frac{c}{c_1}[/math] und [math]n_2 = \frac{c}{c_2} [/math] (Beträgt der Brechungsindex 2, so ist das Licht in diesem Medium nur halb so schnell wie im Vakuum.)

Damit schreibt sich das Brechungsgesetz so:

[math]\sin(\alpha) \, n_1 = \sin(\beta) \, n_2 \quad \Longleftrightarrow \quad \frac{\sin(\alpha)}{\sin(\beta)} = \frac{n_2}{n_1} [/math]

Ich finde, das macht es nicht übersichtlicher....

Sonstiges

• Video der Reflektion am losen und festen Ende bei einer Wellenmaschine (Drehpendelkette).
  

  

Links

• Bilder einer Wellenwanne von der Uni Harvard: "Harvard Natural Sciences Lecture Demonstrations"