Energieübertragung mit einer Kraft (Goldene Regel der Mechanik): Unterschied zwischen den Versionen
(→Eine Rampe (die schiefe Ebene)) |
(→Goldene Regel der Mechanik) |
||
| Zeile 76: | Zeile 76: | ||
==Goldene Regel der Mechanik== | ==Goldene Regel der Mechanik== | ||
| − | Überträgt man Energie mit Hilfe einer Kraft, so kann man | + | Überträgt man Energie mit Hilfe einer Kraft, so kann man mit Hilfe einer Maschine durch eine Hebelwirkung mit einer geringen Kraft ziehen oder drücken - auf Kosten einer längeren Wegstrecke. Oder man kann entlang eines kurzen Weges drücken - auf Kosten einer großen Kraft. |
| + | |||
| + | Das Produkt aus Kraft und Weg ist immer gleichgroß, weshalb man es als die übertragene Energiemenge festgelegt hat. Die "goldene Regel der Mechanik" ist also ein Spezialfall der allgemeinen Energieerhaltung. | ||
Kennt man umgekehrt die Veränderung der Energiemenge und die Wegstrecke, so kann man daraus die wirkende Kraft berechnen: | Kennt man umgekehrt die Veränderung der Energiemenge und die Wegstrecke, so kann man daraus die wirkende Kraft berechnen: | ||
| Zeile 87: | Zeile 89: | ||
<br>ist immer die Menge der übertragenen Energie: | <br>ist immer die Menge der übertragenen Energie: | ||
| − | :<math>\Delta E = F \, \Delta s \qquad \rm 1\, J = 1\, Nm \qquad \ | + | :<math>\Delta E = F \, \Delta s \qquad \rm 1\, J = 1\, Nm \qquad \mathrm{(\ddot u bertragene \ Energie = Kraft \cdot Weg)} </math> |
Mit Maschinen kann man die wirkende Kraft verkleinern aber keine Energie sparen. | Mit Maschinen kann man die wirkende Kraft verkleinern aber keine Energie sparen. | ||
| − | :<math>F = \frac{\Delta E}{\Delta s} \qquad \mathrm{\frac{1\, J}{1\, m}} \qquad \ | + | :<math>F = \frac{\Delta E}{\Delta s} \qquad \quad \mathrm{1\,N = \frac{1\, J}{1\, m}} \qquad \mathrm{(Kraft = Energie\ddot a nderung\ pro\ Weg)}</math> |
Die Kraft gibt an, wie stark sich die Energiemenge mit dem Ort verändert. | Die Kraft gibt an, wie stark sich die Energiemenge mit dem Ort verändert. | ||
Version vom 6. Dezember 2014, 22:09 Uhr
Inhaltsverzeichnis
Beispiele
Lance Armstrong 2004
Auf Indonesien
Kettenschaltung
Das wird nicht einfach, den Wagen da hochzuschieben!
Diese Passtraße schlängelt sich den Berg hinauf.
Die Baldwin Street in Neuseeland ist die steilste Straße der Welt!
Mit diesem Kran kann man schwere Lasten heben.
Die Gangschaltung beim Radfahren
- Wo kommt die Energie beim Radfahren her und wo geht sie hin?
- Sie kommt aus der radelnden Person, die ihre Energie vom Essen erhält.
- Die Energie wird auf die Bewegung des Fahrrades übertragen. Durch die Reibung an der Luft, am Boden, der Kette usw. wird die Energie auf die Bewegung der Luft, die Erwärmung des Bodens und verschiedener anderer mechanischen Teile übertragen.
- Wie funktioniert die Gangschaltung und was bringt sie mir?
- Hat das Zahnrad an der Tretkurbel ("Kettenblatt") viele Zähne und das hintere Zahnrad ("Ritzel") wenige, so dreht sich das Hinterad bei einer Pedalumdrehung ganz oft.
- Durch ein großes Ritzel kann man erreichen, dass man mit einer ganz geringen Kraft treten kann!
- Mit einem großen Gang spar ich mir das viele Treten und den damit verbundenen Aufwand!?
- Nein, das geht nicht, denn wenn man wenig Kurbeln muss, muss man dafür im Gegenzug sehr fest Reintreten!
Bergauf und Bergab Fahren (die schiefe Ebene)
- Aufbau
Ein Wagen wird nach oben auf zwei gestapelte Holzbalken gehoben. Entweder man hebt ihn direkt hoch oder man benutzt ein Brett als Rampe.
Die beiden Holzklötze sind zusammen 15cm hoch, die Bretter ca. 30cm und 60cm lang.
So kann man messen mit welcher Kraft man den Wagen nach oben ziehen muss.
- Beobachtung
Der Wagen muss mit einer Kraft von 2N gehalten werden.
1N
0,5N
0,5N
0,25N
- Animation
Elisabeth und Daniel besteigen den gleichen Berg. Elisabeth nimmt den steilen Weg und Daniel den flachen.
Die Steilheit des Anstiegs kann man durch das Verschieben der hellgrünen Startpunkte verändern.
Man kann auch Daniel und Elisabeth auf dem Weg verschieben.
In der Darstellung kann man sehen mit welcher Kraft sie parallel zum Hang hinuntergedrückt werden.
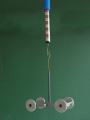
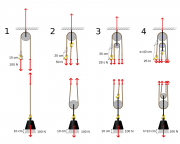
Animation: Ein Flaschenzug
Am Seilende kann man ziehen, um die Kiste nach oben zu heben.
- Mit welcher Kraft muss man am Seilende ziehen? (Eine Einheit entspricht 10N.)
- Wie weit muss man das Seilende nach oben ziehen, um die Kiste einen Meter anzuheben?
Goldene Regel der Mechanik
Überträgt man Energie mit Hilfe einer Kraft, so kann man mit Hilfe einer Maschine durch eine Hebelwirkung mit einer geringen Kraft ziehen oder drücken - auf Kosten einer längeren Wegstrecke. Oder man kann entlang eines kurzen Weges drücken - auf Kosten einer großen Kraft.
Das Produkt aus Kraft und Weg ist immer gleichgroß, weshalb man es als die übertragene Energiemenge festgelegt hat. Die "goldene Regel der Mechanik" ist also ein Spezialfall der allgemeinen Energieerhaltung.
Kennt man umgekehrt die Veränderung der Energiemenge und die Wegstrecke, so kann man daraus die wirkende Kraft berechnen:
- [math]F = \frac{\Delta E}{\Delta s} [/math]
Die Kraft gibt also an, wie stark sich die Energie mit dem Ort verändert.
|
Das Produkt aus wirkender Kraft parallel zum Weg und der Weglänge
Mit Maschinen kann man die wirkende Kraft verkleinern aber keine Energie sparen.
Die Kraft gibt an, wie stark sich die Energiemenge mit dem Ort verändert. |
Kraftwirkung ohne Bewegung (Halten)
Hängt man die Tasche an einen Haken, so wird für das Halten keine Energie benötigt! Aus Sicht der goldenen Regel ist das logisch, denn der zurückgelegte Weg beträgt [math]\rm 0\, m[/math], also ist [math]E= F \cdot s = F\cdot 0\,\rm m = 0\, J[/math]. Allgemein kann man also sagen:
|
Wirkt eine Kraft ohne Bewegung ("Haltekraft"), so wird keine Energie übertragen. |
- Aber wieso ist dann das Halten einer schweren Tasche so anstrengend?
- Das hängt mit der Funktionsweise der Muskeln zusammen:
- Video: Der Mensch als Kraftmaschine (vor allem beim Sport)
Energiezuwachs oder Abnahme
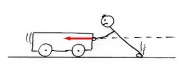
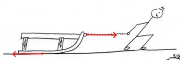
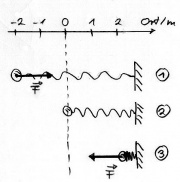
Das Männchen übt eine Kraft F in Richtung des Weges s auf den Wagen aus. Dabei wird die Energie [math]E=F\, s[/math] vom Männchen auf den Wagen übertragen. Das kann man daran sehen, dass der Wagen schneller wird. Der Wagen erhält kinetische Energie (Bewegungsenergie).
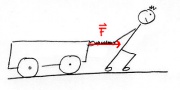
In diesem Fall übt das Männchen eine Kraft aus, die der Bewegungsrichtung des Wagens entgegengesetzt ist. Dabei rutscht es über den Boden. Der Wagen verliert bei diesem Vorgang seine kinetische Energie [math]E=F\, s[/math] und diese wird durch die Reibung des Männchens mit dem Untergrund in Wärmeenergie umgewandelt (auf Entropie umgeladen).
Das Männchen zieht den Schlitten mit konstanter Geschwindigkeit. Wegen der Reibung ist dazu eine Kraft nötig!
Die Kraft in Richtung der Bewegung überträgt also die Energie in die Bewegung des Schlittens und die gleichgroße Reibungskraft sorgt dafür, dass die Energie [math]E=F\, s[/math] gleich wieder von der Bewegung auf die Wärme der Kufen und des Schnees übertragen wird.
Schräg wirkende Kraft
Fahrradfahren
Beim Anfahren stellt man am besten die Pedale in eine "günstige" Position. Warum eigentlich?
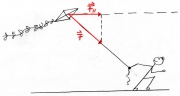
Hier übt das Männchen eine Kraft [math]\vec F[/math] auf den Drachen aus. Da diese jedoch schräg zur Bewegungsrichtung des Drachens gerichtet ist, wirkt von dieser Kraft effektiv nur die parallel gerichtetete Kraft [math]\vec F_{II}[/math] auf den Drachen. Es wird also nur Energie in der Höhe von [math]F_{II}\cdot s[/math] übertragen.
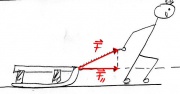
Dieses Beispiel ähnelt dem Beispiel mit dem Drachen, denn auch hier übt das Männchen eine schräg gerichtete Kraft aus. Wir müssen also auch hier wieder die parallel zur Bewegungsrichtung des Schlittens gerichtete Kraft [math]\vec F_{II}[/math] betrachten um herauszufinden, wieviel Energie übertragen wird.
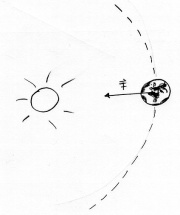
Was passiert, wenn man genau senkrecht zu einer Wegstrecke zieht?
Ein klassisches Beispiel für eine Kreisbewegung: Die Erde dreht sich um die Sonne, wobei die Zentripetalkraft immer senkrecht auf der Bewegungsrichtung ist. Es wird also keine Energie übertragen, sondern lediglich die Bewegungsrichtung verändert.
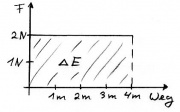
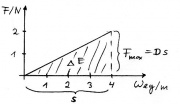
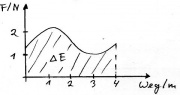
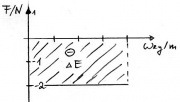
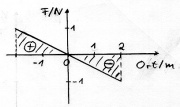
Energiemengen im Weg-Kraft-Diagramm
s-F-Diagramm Fläche ist Energiemenge. Bei konstanter Kraft: E=Fs
Links
- Video: Der Mensch als Kraftmaschine (vor allem beim Sport)
- Benzin sparen beim Autofahren (Karl Sowada)
