Aufgaben zum Elektro-Magnetismus: Unterschied zwischen den Versionen
(→Grundlagen) |
(→Mathematische Anwendung des Induktionsgesetzes) |
||
| Zeile 14: | Zeile 14: | ||
**Nur die Magnetisierung ändert sich, Schleifenfläche und Feldstärke sind konstant. | **Nur die Magnetisierung ändert sich, Schleifenfläche und Feldstärke sind konstant. | ||
| − | == | + | ==Anwendung des Induktionsgesetzes== |
===Primär und Sekundärspule=== | ===Primär und Sekundärspule=== | ||
| − | : | + | [[Datei:Aufgabe_Primär_Sekundärspule.png|thumb|333px]] |
| − | + | [[Datei:Aufgabe_Primär_Sekundärspule_Stromstärkeverlauf_Dreiecksspannung.png|thumb]] | |
| − | + | Innerhalb einer "großen" Primärspule mit 500 Windungen liegt eine "kleine" Sekundärspule mit 2000 Windungen. (Siehe Zeichnung) Durch die Primärspule fließt ein Strom von zwei Ampère. | |
| − | + | ||
| + | Die Spule wird dann von der Spannungsquelle getrennt, wodurch die Stromstärke innerhalb von einer tausendstel Sekunde auf Null Ampère zurückgeht. | ||
| + | |||
| + | Danach legt man an die Primärspule eine Dreiecksspannung mit einer Frequenz von 50Hz an, die zu einer maximalen Stromstärke von 2A führt. (Siehe Zeichnung) | ||
| + | Zur Messung der Spannung an der Sekundärspule wird ein Oszilloskop angeschlossen. | ||
| + | |||
| + | :'''a)''' Wie groß ist zu Beginn die magnetische Feldstärke? Berechnen Sie den magnetischen Fluß durch die Primär- und die Sekündärspule. | ||
| + | :'''b)''' Während des Trennens von der Spannungsquelle registriert die Sekundärspule eine Spannung. Begründen Sie dies und berechnen Sie die Spannung. | ||
| + | :'''c)''' Zeichnen Sie in ein Koordinatensystem den zeitlichen Verlauf der mit dem Oszilloskop gemessenen Induktionsspannung ein. | ||
| + | :Wie ändert sich der Verlauf der Induktionsspannung, wenn die Sekundärspule in einem Winkel von 45° in der Primärspule liegt? | ||
===Eine Spule taucht ein=== | ===Eine Spule taucht ein=== | ||
| Zeile 31: | Zeile 40: | ||
*Ein Permanentmagnet wird über eine Spule gehalten und losgelassen. An die Spule ist ein ein Oszilloskop angeschlossen. | *Ein Permanentmagnet wird über eine Spule gehalten und losgelassen. An die Spule ist ein ein Oszilloskop angeschlossen. | ||
:Zeichnen Sie den zeitlichen Verlauf der gemessenen Induktionsspannung in ein Koordinatensystem und erläutern Sie ihr Ergebnis. | :Zeichnen Sie den zeitlichen Verlauf der gemessenen Induktionsspannung in ein Koordinatensystem und erläutern Sie ihr Ergebnis. | ||
| − | |||
==Energieübertragung== | ==Energieübertragung== | ||
Version vom 26. März 2015, 14:05 Uhr
Inhaltsverzeichnis
Grundlagen
Magnetischer Fluss
- Was ist der magnetische Fluss?
Verschiedene Wege zur Induktionsspannung
- Zählen Sie möglichst viele verschiedene Möglichkeiten auf, wie man experimentell Induktionsspannung an einer Leiterschleife hervorrufen kann und erläutern Sie diese.
Induktionsgesetz
- Wie lautet das Induktionsgesetz in Worten?
- Wie lautet das Induktionsgesetz als Formel in den folgenden Situationen:
- Allgemeingültig
- Nur die Feldstärke ändert sich, Schleifenfläche und Magnetisierung sind konstant.
- Nur die Schleifenfläche ändert sich, die Feldstärke und die Magnetisierung sind konstant.
- Nur die Magnetisierung ändert sich, Schleifenfläche und Feldstärke sind konstant.
Anwendung des Induktionsgesetzes
Primär und Sekundärspule
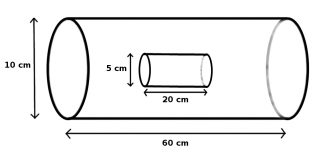
Innerhalb einer "großen" Primärspule mit 500 Windungen liegt eine "kleine" Sekundärspule mit 2000 Windungen. (Siehe Zeichnung) Durch die Primärspule fließt ein Strom von zwei Ampère.
Die Spule wird dann von der Spannungsquelle getrennt, wodurch die Stromstärke innerhalb von einer tausendstel Sekunde auf Null Ampère zurückgeht.
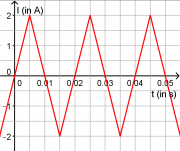
Danach legt man an die Primärspule eine Dreiecksspannung mit einer Frequenz von 50Hz an, die zu einer maximalen Stromstärke von 2A führt. (Siehe Zeichnung) Zur Messung der Spannung an der Sekundärspule wird ein Oszilloskop angeschlossen.
- a) Wie groß ist zu Beginn die magnetische Feldstärke? Berechnen Sie den magnetischen Fluß durch die Primär- und die Sekündärspule.
- b) Während des Trennens von der Spannungsquelle registriert die Sekundärspule eine Spannung. Begründen Sie dies und berechnen Sie die Spannung.
- c) Zeichnen Sie in ein Koordinatensystem den zeitlichen Verlauf der mit dem Oszilloskop gemessenen Induktionsspannung ein.
- Wie ändert sich der Verlauf der Induktionsspannung, wenn die Sekundärspule in einem Winkel von 45° in der Primärspule liegt?
Eine Spule taucht ein
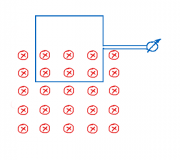
- Eine Spule wird innerhalb von 2 Sekunden in ein homogenes Magnetfeld senkrecht zu den Feldlinien eingetaucht. Die Spule hat einen quadratischen Querschnitt von 5cm Kantenlänge und 300 Windungen und ist an ein Spannungsmessgerät angeschlossen. Die Feldstärke beträgt 1000A/m.
- Berechnen Sie die gemessene Induktionsspannung.
- Was kann man messen, wenn die Spule innerhalb des Feldes bewegt wird?
- Welche Polung hat die Induktionsspannung?
Magnet im freien Fall
- Ein Permanentmagnet wird über eine Spule gehalten und losgelassen. An die Spule ist ein ein Oszilloskop angeschlossen.
- Zeichnen Sie den zeitlichen Verlauf der gemessenen Induktionsspannung in ein Koordinatensystem und erläutern Sie ihr Ergebnis.
Energieübertragung
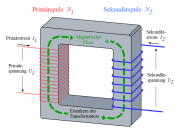
Transformator
- Warum kann man einen Transformator nicht mit Gleichstrom betreiben?
- Erläutern Sie anhand der Zeichnung die Funktionsweise eines Trafos.
- Wie könnte ein Trafo gebaut sein, der ein Handy mit 5,7V Spannung versorgt?
Wirbelstrombremse
- Nennen Sie Beispiele, bei denen eine Wirbelstrombremse eingesetzt wird.
- Erläutern Sie das Funktionsprinzip mit einer Zeichnung.
- Erklären Sie dabei mit Hilfe des Induktionsgesetzes, wie die Ströme fließen.
- Wie kann man die Bremswirkung mit der Energieerhaltung begründen?
Selbstinduktion und Energie des Magnetfeldes
Ein Versuch
- Erklären Sie den Begriff der Selbstinduktion anhand eines Versuchs.
- Begründen Sie, warum die Spannung der Selbstinduktion an einer Spule proportional zur Änderung der Stromstärke ist.
Induktivität
- Eine Spule hat eine Induktivität von 10 H (Henry).
- Was bedeutet das?
- Eine Spule hat 1000 Windungen und einen geschlossenen Eisenkern mit einer Permeabilitätszahl von [math]\mu_r = 2000[/math].
- Berechnen Sie ihre Induktivität.
Elektrische Wirbelfelder
Alte Aufgaben
Induktion und Selbstinduktion
Damit die in der letzten Woche und evt. in dieser Woche ausgefallenen Stunden etwas kompensiert werden können hier nun ihre Hausafgaben bis Do, bzw. Fr.: [bearbeiten] Aus Dorn Bader, Seite 59 (Kopie mit dem Bändchenmikrophon)
* Aufgabe 2 * Aufgabe 3 * Aufgabe 4
[bearbeiten]
Lösungshinweise
* Lesen Sie sich nochmal die Seite über das Induktionsgesetz durch.
* DB, A1: Dieser Typ von Induktion ist ja auch auf dieser Seite beschrieben. Man interpretiert das Eintauchen als Änderung der effektiven Fläche.
LaTex: \dot A = \mathrm{1 \frac{mm}{s} \cdot 60mm = 60 \frac{mm^2}{s} \, (=\frac{\Delta A}{\Delta t}=\frac{\Delta s \cdot 6cm}{\Delta t})}
Zur Ermittlung der Polung dient die UVW-Regel.
* DB,A2:
Zu a) und b): Es ist wichtig, dass kein Strom fliesst. Die Schleife befindet sich im freien Fall. (LaTex: s=1/2\,g\,t^2 und LaTex: v=g\,t) Zu c): Entscheident ist wieder die Flächenänderung. Eintauchen: LaTex: A(t)=v(t)\cdot 6cm Mittendrin: LaTex: U=0 (Wieso?) Austritt: LaTex: A(t)=-v(t)\cdot 6cm (Wieso anderes Vorzeichen?)
* DB, A4:
Zu a): Offensichtlich führt eine Flächenänderung zur Induktionsspannung. LaTex: U \approx \frac{\Delta A}{\Delta t}\,B
Zu b): Lesen Sie noch einmal die drehende Fläche. LaTex: \Delta A = A_0-A_0\,\cos(\alpha)