Animation: Schnitt von Geraden; Flugzeug-Aufgabe (Lösungen): Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „Zurück zur Aufgabe Verwende die Animation, um die Antworten abzulesen: # #An welchem Punkt kreuzen sic…“) |
(→3. Um wieviel Uhr ist das blaue und um wieviel Uhr das rote Flugzeug am Schnittpunkt der Flugbahnen?) |
||
| (19 dazwischenliegende Versionen des gleichen Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | __NOTOC__ | ||
[[Animation: Schnitt von Geraden; Flugzeug-Aufgabe|Zurück zur Aufgabe]] | [[Animation: Schnitt von Geraden; Flugzeug-Aufgabe|Zurück zur Aufgabe]] | ||
Verwende die Animation, um die Antworten abzulesen: | Verwende die Animation, um die Antworten abzulesen: | ||
| − | + | =====1.===== | |
| − | + | =====2. An welchem Punkt kreuzen sich die Flugbahnen?===== | |
| − | + | Sie kreuzen sich im Punkt <math>S(12|6)</math>. | |
| − | + | =====3. Um wieviel Uhr ist das blaue und um wieviel Uhr das rote Flugzeug am Schnittpunkt der Flugbahnen?===== | |
| − | + | Das blaue Flugzeug ist um 12:03 Uhr am Schnittpunkt, das rote schon eine Minute früher, um 12:02 Uhr. | |
| − | + | =====4. Um wieviel Uhr sind sich die Flugzeuge am nächsten? (Ersetze dazu das Flugzeug durch den markierten Punkt!)===== | |
| − | + | Um ca. 12:02 Uhr und 20 Sekunden sind sie sich am nächsten. | |
| − | + | =====5. Wie nahe kommen sich die Flugzeuge?===== | |
| − | + | Der geringste Abstand beträgt ca. 1,66km. | |
| − | + | =====6. Um wieviel Uhr sind beide Flugzeuge gleich hoch? Wie hoch sind sie dann?===== | |
| − | + | Um ca. 12:04 Uhr sind beide Flugzeuge 8km hoch. | |
| − | Stelle nun je eine Geradengleichung mit dem Parameter t für die Bewegung der Flugzeuge auf und berechne damit die Antworten: | + | =====Stelle nun je eine Geradengleichung mit dem Parameter t für die Bewegung der Flugzeuge auf und berechne damit die Antworten:===== |
| + | *Für das blaue Flugzeug: | ||
| + | :Zu Beginn der Zeitmessung (<math>t=0</math>) befindet sich das blaue Flugzeug im Punkt <math>\rm A(0|0)</math>, eine Minute später (<math>t=1</math>) im Punkt <math>\rm B(4|2)</math>. | ||
| + | :Deshalb muss man den Vektor <math>\vec a = \begin{pmatrix} 0 \\0 \end{pmatrix}</math> als Stützvektor wählen und den Vektor <math>\vec {\rm AB} = \vec b - \vec a = \begin{pmatrix} 4 \\2 \end{pmatrix}</math> als Richtungsvektor: | ||
| + | ::<math>g_{blau}: \quad \vec x = t \begin{pmatrix} 4 \\2 \end{pmatrix}</math> | ||
| + | *Für das rote Flugzeug: | ||
| + | :Zu Beginn der Zeitmessung ( <math>t=0</math>) befindet sich das rote Flugzeug im Punkt <math>\rm C(28|4)</math>, eine Minute später (<math>t=1</math>) im Punkt <math>\rm D(20|5)</math>. | ||
| + | :Deshalb muss man den Vektor <math>\rm \vec c = \begin{pmatrix} 28 \\4 \end{pmatrix}</math> als Stützvektor wählen und den Vektor <math>\vec {\rm CD} = \vec d - \vec c = \begin{pmatrix} -8 \\1 \end{pmatrix}</math> als Richtungsvektor: | ||
| + | ::<math>g_{rot}: \quad \vec x = \begin{pmatrix} 28 \\4 \end{pmatrix} + t \begin{pmatrix} -8 \\1 \end{pmatrix}</math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | =====1. Berechne die Geschwindigkeit der beiden Flugzeuge zunächst in km pro Minute und dann in km pro Stunde.===== | |
| + | |||
| + | :*Das blaue Flugzeug ist um 12:00 Uhr am Koordinatenursprung <math>\rm A(0|0)</math>, eine Minute später ist es am Punkt <math>\rm B(4|2)</math>. Die Strecke <math>\rm AB</math> hat eine Länge von: | ||
| + | :::<math>\rm { \left| \vec{AB}\right| = \left| \vec b - \vec a \right| = \left| \begin{pmatrix} 4 \\2 \end{pmatrix} \right| = \sqrt{4^2 +2^2} =\sqrt{20} \approx 4{,47}\, (km) }</math> | ||
| + | ::Das blaue Flugzeug hat also eine Geschwindigkeit von <math>4{,}47\,\rm \frac{km}{min}</math>. In einer Stunde fliegt es 60-mal soweit, also beträgt die Geschwindigkeit in Kilometer pro Stunde: | ||
| + | :::<math>v_{blau}= 60 \cdot 4{,}47 \,\rm \frac{km}{h} \approx 286\,\rm \frac{km}{h}</math>. | ||
| + | |||
| + | :*Für das rote Flugzeug ergibt sich entsprechend: | ||
| + | :::<math>\rm { \left| \vec{CD}\right| = \left| \vec d - \vec c \right| = \left| \begin{pmatrix} -8 \\1 \end{pmatrix} \right| = \sqrt{(-8)^2 +1^2} =\sqrt{65} \approx 8{,06}\, (km) }</math> | ||
| + | ::Das rote Flugzeug hat also eine Geschwindigkeit von <math>8{,}06\,\rm \frac{km}{min}</math> oder, in Kilometer pro Stunde: | ||
| + | :::<math>v_{blau}= 60 \cdot 8{,}06 \,\rm \frac{km}{h} \approx 484\,\rm \frac{km}{h}</math>. | ||
| + | |||
| + | =====2. An welchem Punkt kreuzen sich die Flugbahnen?===== | ||
| + | =====3. Um wieviel Uhr ist das blaue und um wieviel Uhr das rote Flugzeug am Schnittpunkt der Flugbahnen?===== | ||
| + | Um den Schnittpunkt der Flugbahnen zu berechnen, setzt man die Geradengleichungen gleich: | ||
| + | |||
| + | :<math> | ||
| + | \begin{array}{rcl} | ||
| + | \vec x_{blau} &=& \vec x_{rot} \\ | ||
| + | t \begin{pmatrix} 4 \\2 \end{pmatrix} &=& \begin{pmatrix} 28 \\4 \end{pmatrix} + t \begin{pmatrix} -8 \\1 \end{pmatrix} \\ | ||
| + | \end{array} | ||
| + | </math> | ||
| + | Wenn man diese Gleichung löst, so stellt man fest, dass es keine Lösung für t gibt! Das ist auch nicht verwunderlich, denn zu allen Zeiten t sind die beiden Flugzeuge nicht am gleichen Ort, sie kollidieren nicht. | ||
| + | |||
| + | Deshalb muss man zur Berechnung des Schnittpunktes zwei verschiedene Parameter <math>t_b</math> und <math>t_r</math> wählen. Beide Flugzeuge sind ja zu verschiedenen Zeiten am Schnittpunkt! | ||
| + | |||
| + | :<math> | ||
| + | \begin{array}{rcl} | ||
| + | t_b \begin{pmatrix} 4 \\2 \end{pmatrix} &=& \begin{pmatrix} 28 \\4 \end{pmatrix} + t_r \begin{pmatrix} -8 \\1 \end{pmatrix} \\ | ||
| + | \end{array} | ||
| + | </math> | ||
| + | Die Gleichung bringt man nun in Standardform und schreibt sie in Koordinaten auf. Man erhält ein lineares Gleichungssystem mit zwei Gleichungen und zwei Unbekannten: | ||
| + | |||
| + | :<math> | ||
| + | \begin{array}{rcl} | ||
| + | t_b \begin{pmatrix} 4 \\2 \end{pmatrix} - t_r \begin{pmatrix} -8 \\1 \end{pmatrix} &=& \begin{pmatrix} 28 \\4 \end{pmatrix} \\ | ||
| + | \end{array} | ||
| + | </math> | ||
| + | |||
| + | :<math> | ||
| + | \begin{array}{rrrcll} | ||
| + | \rm (I) & 4\,t_b & +8\,t_r &=& 28 \\ | ||
| + | \rm (II) & 2\,t_b& -t_r &=& 4 & \\ | ||
| + | \end{array} | ||
| + | </math> | ||
| + | |||
| + | :<math> | ||
| + | \begin{array}{rrrcll} | ||
| + | \rm (I') & 4\,t_b & +8\,t_r &=& 28 \\ | ||
| + | \rm (II') & & 10\,t_r &=& 20 & (\rm{I - 2\, II}) \\ | ||
| + | \end{array} | ||
| + | </math> | ||
| + | |||
| + | Aus <math>\rm (II')</math> folgt <math>t_r = 2</math>. Dies in <math>\rm (I)</math> einsetzen: | ||
| + | :<math> | ||
| + | \begin{array}{rcl} | ||
| + | 4\,t_b +8\cdot 2 &=& 28 & | \quad -16\\ | ||
| + | 4\,t_b &=& 12 &|\quad :4\\ | ||
| + | t_b &=& 3\\ | ||
| + | \end{array} | ||
| + | </math> | ||
| + | |||
| + | Das rote Flugzeug ist also um 12:02 Uhr am Schnittpunkt der Flugbahnen, das blaue erst eine Minute später, um 12:03 Uhr. | ||
| + | |||
| + | Den Schnittpunkt erhält man durch einsetzen von <math>t_r</math> oder <math>t_r</math> in die jeweilige Geradengleichung: | ||
| + | |||
| + | :<math> | ||
| + | \begin{array}{rclcl} | ||
| + | \vec x_{rot} &=& \begin{pmatrix} 28 \\4 \end{pmatrix} + 2 \begin{pmatrix} -8 \\ 1\end{pmatrix} &=& \begin{pmatrix} 12 \\16 \end{pmatrix} \\ | ||
| + | \vec x_{blau} &=& 3 \begin{pmatrix} 4 \\2 \end{pmatrix} &=& \begin{pmatrix} 12 \\16 \end{pmatrix} \\ | ||
| + | \end{array} | ||
| + | </math> | ||
| + | |||
| + | =====4. Siehe unten===== | ||
| + | =====5. Siehe unten===== | ||
| + | =====6. Um wieviel Uhr sind beide Flugzeuge gleich hoch? Wie hoch sind sie dann?===== | ||
| + | Gleiche Höhe bedeutet gleiche <math>x_2-</math>Koordinate. Man setzt daher die <math>x_2-</math>Koordinaten aus den Geradengleichungen gleich. Dabei verwendet man ''nur einen'' Parameter, die gemeinsame Zeit, denn die Flugzeuge sollen ja gleichzeitig auf der selben Höhe sein! | ||
| + | |||
| + | :<math> | ||
| + | \begin{array}{rcll} | ||
| + | \rm Höhe_{blau} &=& \rm Höhe_{rot} \\ | ||
| + | (*) \quad 2 t &=& 4 + t & |\quad -t\\ | ||
| + | t &=& 4\\ | ||
| + | \end{array} | ||
| + | </math> | ||
| + | |||
| + | Beide Flugzeuge sind um 12:04 auf der gleichen Höhe. Setzt man <math>t</math> in <math>(*)</math> ein, so erhält man die Höhe: | ||
| + | |||
| + | :<math> | ||
| + | \begin{array}{rcll} | ||
| + | 2 \cdot 4 &=& 4 + 4\\ | ||
| + | 8 &=& 8\\ | ||
| + | \end{array} | ||
| + | </math> | ||
| + | |||
| + | Beide Flugzeuge sind 8km hoch. | ||
| + | |||
| + | |||
| + | |||
| + | ---- | ||
| + | |||
| + | =====7. Berechne um wieviel Uhr die Flugzeuge den geringsten Abstand haben und wie weit sie dann voneinander entfernt sind.===== | ||
:(Hinweis: Berechne den Abstand d(t) in Abhängigkeit von der Zeit t. Finde mit dem GTR den Tiefpunkt des Funktionsgraphen.) | :(Hinweis: Berechne den Abstand d(t) in Abhängigkeit von der Zeit t. Finde mit dem GTR den Tiefpunkt des Funktionsgraphen.) | ||
| + | |||
| + | Der Abstand <math>d</math> zwischen den Flugzeugen ist die Länge der Verbindungslinie, also der Strecke <math>\rm{X_{blau} X_{rot}}</math>: | ||
| + | |||
| + | :<math>d = \left| \rm{X_{blau} X_{rot}} \right| = \left| \vec{x_{rot}} - \vec{x_{blau}} \right| </math> | ||
| + | Die Geradengleichungen geben den Ort der Flugzeuge an, und man kann sie einsetzen: | ||
| + | :<math>d = \left| \begin{pmatrix} 28-8\,t \\ 4+\,t \end{pmatrix} - \begin{pmatrix} 4\,t \\ 2\,t \end{pmatrix} \right| = \left| \begin{pmatrix} 28-8\,t -4\,t \\ 4+\,t-2\,t \end{pmatrix} \right| = \left| \begin{pmatrix} 28-12\,t \\ 4-\,t \end{pmatrix}\right| </math> | ||
| + | Mit dem Satz des Pythagoras berechnet man den Betrag: | ||
| + | :<math>d(t) = \sqrt{(28-12\,t)^2+(4-\,t)^2} </math> | ||
| + | Die Quadrate unter der Wurzel könnte man noch ausrechnen und dann zusammenfassen, dabei verrechnet man sich jedoch häufig und es ist nicht notwendig. Es sei denn, man hat einen Algebra-fähigen Taschenrechner oder man verwendet [http://www.wolframalpha.com/ Wolfram Alpha], dann erhält man: | ||
| + | :<math>d(t) = \sqrt{800 -680\,t +145\,t^2} </math> | ||
| + | |||
| + | Um den minimalen Abstand zu finden, kann man nun mit einem Taschenrechner das Minimum der Funktion <math>d(t)</math> finden: | ||
| + | [[Datei:Flugzeugaufgabe Minimum Abstandsfunktion.png|610px]] | ||
| + | |||
| + | Für die Zeit <math>t=2{,}3448</math> ist der Abstand mit <math>1{,}6609\,\rm km</math> am geringsten. Die Zeit in Minuten kann man noch in Minuten und Sekunden umrechnen, den Abstand auf Meter runden: | ||
| + | |||
| + | Die Flugzeuge haben um 12 Uhr 2 Minuten und 21 Sekunden mit 1661 Metern den geringsten Abstand. | ||
Aktuelle Version vom 24. Juni 2018, 22:41 Uhr
Verwende die Animation, um die Antworten abzulesen:
1.
2. An welchem Punkt kreuzen sich die Flugbahnen?
Sie kreuzen sich im Punkt [math]S(12|6)[/math].
3. Um wieviel Uhr ist das blaue und um wieviel Uhr das rote Flugzeug am Schnittpunkt der Flugbahnen?
Das blaue Flugzeug ist um 12:03 Uhr am Schnittpunkt, das rote schon eine Minute früher, um 12:02 Uhr.
4. Um wieviel Uhr sind sich die Flugzeuge am nächsten? (Ersetze dazu das Flugzeug durch den markierten Punkt!)
Um ca. 12:02 Uhr und 20 Sekunden sind sie sich am nächsten.
5. Wie nahe kommen sich die Flugzeuge?
Der geringste Abstand beträgt ca. 1,66km.
6. Um wieviel Uhr sind beide Flugzeuge gleich hoch? Wie hoch sind sie dann?
Um ca. 12:04 Uhr sind beide Flugzeuge 8km hoch.
Stelle nun je eine Geradengleichung mit dem Parameter t für die Bewegung der Flugzeuge auf und berechne damit die Antworten:
- Für das blaue Flugzeug:
- Zu Beginn der Zeitmessung ([math]t=0[/math]) befindet sich das blaue Flugzeug im Punkt [math]\rm A(0|0)[/math], eine Minute später ([math]t=1[/math]) im Punkt [math]\rm B(4|2)[/math].
- Deshalb muss man den Vektor [math]\vec a = \begin{pmatrix} 0 \\0 \end{pmatrix}[/math] als Stützvektor wählen und den Vektor [math]\vec {\rm AB} = \vec b - \vec a = \begin{pmatrix} 4 \\2 \end{pmatrix}[/math] als Richtungsvektor:
- [math]g_{blau}: \quad \vec x = t \begin{pmatrix} 4 \\2 \end{pmatrix}[/math]
- Für das rote Flugzeug:
- Zu Beginn der Zeitmessung ( [math]t=0[/math]) befindet sich das rote Flugzeug im Punkt [math]\rm C(28|4)[/math], eine Minute später ([math]t=1[/math]) im Punkt [math]\rm D(20|5)[/math].
- Deshalb muss man den Vektor [math]\rm \vec c = \begin{pmatrix} 28 \\4 \end{pmatrix}[/math] als Stützvektor wählen und den Vektor [math]\vec {\rm CD} = \vec d - \vec c = \begin{pmatrix} -8 \\1 \end{pmatrix}[/math] als Richtungsvektor:
- [math]g_{rot}: \quad \vec x = \begin{pmatrix} 28 \\4 \end{pmatrix} + t \begin{pmatrix} -8 \\1 \end{pmatrix}[/math]
1. Berechne die Geschwindigkeit der beiden Flugzeuge zunächst in km pro Minute und dann in km pro Stunde.
- Das blaue Flugzeug ist um 12:00 Uhr am Koordinatenursprung [math]\rm A(0|0)[/math], eine Minute später ist es am Punkt [math]\rm B(4|2)[/math]. Die Strecke [math]\rm AB[/math] hat eine Länge von:
- [math]\rm { \left| \vec{AB}\right| = \left| \vec b - \vec a \right| = \left| \begin{pmatrix} 4 \\2 \end{pmatrix} \right| = \sqrt{4^2 +2^2} =\sqrt{20} \approx 4{,47}\, (km) }[/math]
- Das blaue Flugzeug hat also eine Geschwindigkeit von [math]4{,}47\,\rm \frac{km}{min}[/math]. In einer Stunde fliegt es 60-mal soweit, also beträgt die Geschwindigkeit in Kilometer pro Stunde:
- [math]v_{blau}= 60 \cdot 4{,}47 \,\rm \frac{km}{h} \approx 286\,\rm \frac{km}{h}[/math].
- Für das rote Flugzeug ergibt sich entsprechend:
- [math]\rm { \left| \vec{CD}\right| = \left| \vec d - \vec c \right| = \left| \begin{pmatrix} -8 \\1 \end{pmatrix} \right| = \sqrt{(-8)^2 +1^2} =\sqrt{65} \approx 8{,06}\, (km) }[/math]
- Das rote Flugzeug hat also eine Geschwindigkeit von [math]8{,}06\,\rm \frac{km}{min}[/math] oder, in Kilometer pro Stunde:
- [math]v_{blau}= 60 \cdot 8{,}06 \,\rm \frac{km}{h} \approx 484\,\rm \frac{km}{h}[/math].
2. An welchem Punkt kreuzen sich die Flugbahnen?
3. Um wieviel Uhr ist das blaue und um wieviel Uhr das rote Flugzeug am Schnittpunkt der Flugbahnen?
Um den Schnittpunkt der Flugbahnen zu berechnen, setzt man die Geradengleichungen gleich:
- [math] \begin{array}{rcl} \vec x_{blau} &=& \vec x_{rot} \\ t \begin{pmatrix} 4 \\2 \end{pmatrix} &=& \begin{pmatrix} 28 \\4 \end{pmatrix} + t \begin{pmatrix} -8 \\1 \end{pmatrix} \\ \end{array} [/math]
Wenn man diese Gleichung löst, so stellt man fest, dass es keine Lösung für t gibt! Das ist auch nicht verwunderlich, denn zu allen Zeiten t sind die beiden Flugzeuge nicht am gleichen Ort, sie kollidieren nicht.
Deshalb muss man zur Berechnung des Schnittpunktes zwei verschiedene Parameter [math]t_b[/math] und [math]t_r[/math] wählen. Beide Flugzeuge sind ja zu verschiedenen Zeiten am Schnittpunkt!
- [math] \begin{array}{rcl} t_b \begin{pmatrix} 4 \\2 \end{pmatrix} &=& \begin{pmatrix} 28 \\4 \end{pmatrix} + t_r \begin{pmatrix} -8 \\1 \end{pmatrix} \\ \end{array} [/math]
Die Gleichung bringt man nun in Standardform und schreibt sie in Koordinaten auf. Man erhält ein lineares Gleichungssystem mit zwei Gleichungen und zwei Unbekannten:
- [math] \begin{array}{rcl} t_b \begin{pmatrix} 4 \\2 \end{pmatrix} - t_r \begin{pmatrix} -8 \\1 \end{pmatrix} &=& \begin{pmatrix} 28 \\4 \end{pmatrix} \\ \end{array} [/math]
- [math] \begin{array}{rrrcll} \rm (I) & 4\,t_b & +8\,t_r &=& 28 \\ \rm (II) & 2\,t_b& -t_r &=& 4 & \\ \end{array} [/math]
- [math] \begin{array}{rrrcll} \rm (I') & 4\,t_b & +8\,t_r &=& 28 \\ \rm (II') & & 10\,t_r &=& 20 & (\rm{I - 2\, II}) \\ \end{array} [/math]
Aus [math]\rm (II')[/math] folgt [math]t_r = 2[/math]. Dies in [math]\rm (I)[/math] einsetzen:
- [math] \begin{array}{rcl} 4\,t_b +8\cdot 2 &=& 28 & | \quad -16\\ 4\,t_b &=& 12 &|\quad :4\\ t_b &=& 3\\ \end{array} [/math]
Das rote Flugzeug ist also um 12:02 Uhr am Schnittpunkt der Flugbahnen, das blaue erst eine Minute später, um 12:03 Uhr.
Den Schnittpunkt erhält man durch einsetzen von [math]t_r[/math] oder [math]t_r[/math] in die jeweilige Geradengleichung:
- [math] \begin{array}{rclcl} \vec x_{rot} &=& \begin{pmatrix} 28 \\4 \end{pmatrix} + 2 \begin{pmatrix} -8 \\ 1\end{pmatrix} &=& \begin{pmatrix} 12 \\16 \end{pmatrix} \\ \vec x_{blau} &=& 3 \begin{pmatrix} 4 \\2 \end{pmatrix} &=& \begin{pmatrix} 12 \\16 \end{pmatrix} \\ \end{array} [/math]
4. Siehe unten
5. Siehe unten
6. Um wieviel Uhr sind beide Flugzeuge gleich hoch? Wie hoch sind sie dann?
Gleiche Höhe bedeutet gleiche [math]x_2-[/math]Koordinate. Man setzt daher die [math]x_2-[/math]Koordinaten aus den Geradengleichungen gleich. Dabei verwendet man nur einen Parameter, die gemeinsame Zeit, denn die Flugzeuge sollen ja gleichzeitig auf der selben Höhe sein!
- [math] \begin{array}{rcll} \rm Höhe_{blau} &=& \rm Höhe_{rot} \\ (*) \quad 2 t &=& 4 + t & |\quad -t\\ t &=& 4\\ \end{array} [/math]
Beide Flugzeuge sind um 12:04 auf der gleichen Höhe. Setzt man [math]t[/math] in [math](*)[/math] ein, so erhält man die Höhe:
- [math] \begin{array}{rcll} 2 \cdot 4 &=& 4 + 4\\ 8 &=& 8\\ \end{array} [/math]
Beide Flugzeuge sind 8km hoch.
7. Berechne um wieviel Uhr die Flugzeuge den geringsten Abstand haben und wie weit sie dann voneinander entfernt sind.
- (Hinweis: Berechne den Abstand d(t) in Abhängigkeit von der Zeit t. Finde mit dem GTR den Tiefpunkt des Funktionsgraphen.)
Der Abstand [math]d[/math] zwischen den Flugzeugen ist die Länge der Verbindungslinie, also der Strecke [math]\rm{X_{blau} X_{rot}}[/math]:
- [math]d = \left| \rm{X_{blau} X_{rot}} \right| = \left| \vec{x_{rot}} - \vec{x_{blau}} \right| [/math]
Die Geradengleichungen geben den Ort der Flugzeuge an, und man kann sie einsetzen:
- [math]d = \left| \begin{pmatrix} 28-8\,t \\ 4+\,t \end{pmatrix} - \begin{pmatrix} 4\,t \\ 2\,t \end{pmatrix} \right| = \left| \begin{pmatrix} 28-8\,t -4\,t \\ 4+\,t-2\,t \end{pmatrix} \right| = \left| \begin{pmatrix} 28-12\,t \\ 4-\,t \end{pmatrix}\right| [/math]
Mit dem Satz des Pythagoras berechnet man den Betrag:
- [math]d(t) = \sqrt{(28-12\,t)^2+(4-\,t)^2} [/math]
Die Quadrate unter der Wurzel könnte man noch ausrechnen und dann zusammenfassen, dabei verrechnet man sich jedoch häufig und es ist nicht notwendig. Es sei denn, man hat einen Algebra-fähigen Taschenrechner oder man verwendet Wolfram Alpha, dann erhält man:
- [math]d(t) = \sqrt{800 -680\,t +145\,t^2} [/math]
Um den minimalen Abstand zu finden, kann man nun mit einem Taschenrechner das Minimum der Funktion [math]d(t)[/math] finden:
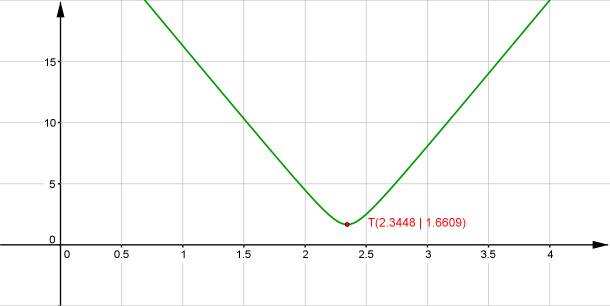
Für die Zeit [math]t=2{,}3448[/math] ist der Abstand mit [math]1{,}6609\,\rm km[/math] am geringsten. Die Zeit in Minuten kann man noch in Minuten und Sekunden umrechnen, den Abstand auf Meter runden:
Die Flugzeuge haben um 12 Uhr 2 Minuten und 21 Sekunden mit 1661 Metern den geringsten Abstand.