*: Unterschied zwischen den Versionen
| (400 dazwischenliegende Versionen des gleichen Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
__NOTOC__ | __NOTOC__ | ||
| − | |||
{| | {| | ||
| − | |height=" | + | |height="1350px"| |
| + | |}__NOTOC__ | ||
| + | ==Aufgaben zur Energie== | ||
| + | ====Energieträger und Energieformen==== | ||
| − | + | '''1)''' Eine Batterie ist ein Energieträger. Denn in der Batterie steckt Energie, mit der man einen Motor antreiben kann. | |
| − | + | *Nenne drei weitere Gegenstände, die auch Energieträger sind und sage, was man mit dieser Energie machen kann. | |
| − | '''1)''' | + | |
| − | + | ||
| − | + | '''2)''' Die Tabelle zeigt, welche verschiedenen Namen man der Energie verschiedener Träger gegeben hat. | |
| − | + | *Nenne für jede Energieform ein ''anderes'' Beispiel in folgender Art: | |
| − | '''2)''' | + | :"Der Wind, also Luft, die sich schnell bewegt, enthält Bewegungsenergie." |
| − | + | ||
| − | : | + | {|class="wikitable" " |
| − | : | + | ! |
| − | + | Energieträger | |
| + | ! colspan="2" "| | ||
| + | Name der Energieform | ||
| + | |- | ||
| | | | ||
| − | [[ | + | Holz |
| + | |colspan="2"|chemische Energie | ||
| + | |- | ||
| + | | | ||
| + | heißes Wasser | ||
| + | |colspan="2"|Wärmeenergie | ||
| + | |- | ||
| + | | | ||
| + | geriebener Luftballon | ||
| + | |colspan="2"|elektrische Energie | ||
| + | |- | ||
| + | | | ||
| + | Licht | ||
| + | |colspan="2"|Lichtenergie<ref>Das Licht selbst besteht nicht aus Energie, es enthält die Energie! Was das Licht selbst ist, kann man nicht so einfach beantworten.</ref> | ||
| + | |- | ||
| + | | | ||
| + | laufender Mensch | ||
| + | |Bewegungsenergie | ||
| + | |rowspan="3"|mechanische Energie | ||
| + | |- | ||
| + | | | ||
| + | [[Media:Luftballon Druecken.jpg|zusammengedrückter Luftballon]] | ||
| + | |Spannenergie | ||
| + | |- | ||
| + | | | ||
| + | hochgelegenes Wasser in einem Stausee | ||
| + | |Lageenergie | ||
|} | |} | ||
| − | |||
| − | |||
| − | + | <br style="clear: both" /> | |
| − | :< | + | |
| − | Der | + | '''3)''' Aus der Tabelle kann man ablesen: |
| + | :"Mit der Energie von 38 Stunden Sonnenlicht auf einen Quadratmeter kann man den Akku eines E-Autos aufladen." | ||
| + | *Bilde drei weitere Sätze in dieser Art. | ||
| + | |||
| + | {|class="wikitable" style="text-align: right; " | ||
| + | !style="border-style: solid; border-width: 5px "| | ||
| + | Gegenstand | ||
| + | |||
| + | !style="border-style: solid; border-width: 5px "| | ||
| + | Energiemenge in Joule | ||
| + | |||
| + | |- | ||
| + | |style="border-style: solid; border-width: 5px "| | ||
| + | Sonnenlicht auf einen m<sup>2</sup> für eine Sekunde | ||
| + | |||
| + | |style="border-style: solid; border-width: 5px "| | ||
| + | 1.300 J | ||
| + | |||
| + | |- | ||
| + | |style="border-style: solid; border-width: 5px "| | ||
| + | ein Liter Benzin | ||
| + | |||
| + | |style="border-style: solid; border-width: 5px "| | ||
| + | 30.000.000 J | ||
| + | |||
| + | |- | ||
| + | |style="border-style: solid; border-width: 5px "| | ||
| + | Akku eines E-Autos<ref>Siehe Wikipedia: [https://de.wikipedia.org/wiki/Tesla_Model_3#Batterietechnik Tesla Model 3]</ref> | ||
| + | |||
| + | |style="border-style: solid; border-width: 5px "| | ||
| + | 180.000.000 J | ||
| + | |||
| + | |- | ||
| + | |style="border-style: solid; border-width: 5px "| | ||
| + | aufgepumpter Fahrradreifen | ||
| + | |||
| + | |style="border-style: solid; border-width: 5px "| | ||
| + | 600 J | ||
| + | |||
| + | |- | ||
| + | |style="border-style: solid; border-width: 5px "| | ||
| + | Schulranzen auf einem ein Meter hohen Tisch | ||
| + | |||
| + | |style="border-style: solid; border-width: 5px "| | ||
| + | 100 J | ||
| + | |||
| + | |- | ||
| + | |style="border-style: solid; border-width: 5px "| | ||
| + | Ein Liter kochendes Wasser<ref>Im Vergleich zu Zimmertemperatur bei 20°C.</ref> | ||
| + | |||
| + | |style="border-style: solid; border-width: 5px "| | ||
| + | 300.000 J | ||
| + | |||
| + | |- | ||
| + | |style="border-style: solid; border-width: 5px "| | ||
| + | Fahrradfahrerin mit 30 km/h | ||
| + | |||
| + | |style="border-style: solid; border-width: 5px "| | ||
| + | 3.000 J | ||
| + | |- | ||
| + | |style="border-style: solid; border-width: 5px "| | ||
| + | eine Tafel Schokolade | ||
| + | |style="border-style: solid; border-width: 5px "| | ||
| + | 2.000.000 J | ||
| + | |||
| + | |} | ||
| + | <br style="clear: both" /> | ||
| + | |||
| + | ==Energiewandler / Energieumlader== | ||
| + | |||
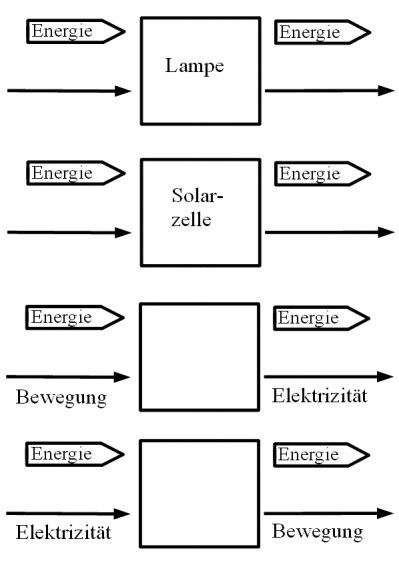
| + | [[Datei:Aufgaben_Energieumlader.png|399px|left]] | ||
| + | '''4) Energie für Maschinen''' | ||
| + | |||
| + | Ein Automotor bekommt mit dem Benzin seine Energie und setzt damit das Auto in Bewegung. Der Motor wird dabei auch sehr heiss. Der Motor lädt die Energie vom Benzin auf die Bewegung des Autos und auf den heissen Motor um. | ||
| + | :'''a)''' Trage in die Energieumladerdiagramme die passenden Energieträger oder den Namen des Umladers ein! | ||
| + | :'''b)''' Wie kann man Energie von Licht auf Bewegung umladen? Zeichne dazu zwei geeignete Energieumlader hintereinander. | ||
| + | <br style="clear: both" /> | ||
| + | |||
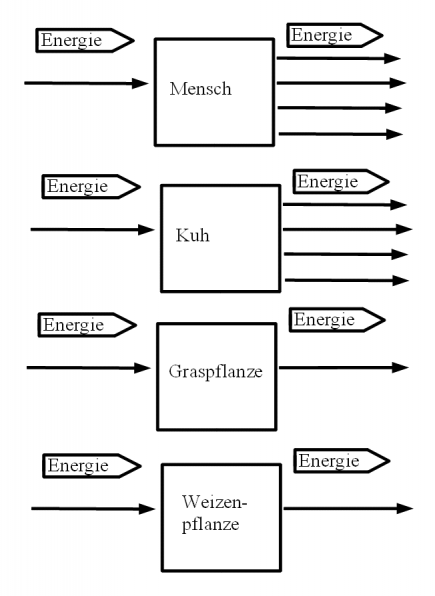
| + | [[Datei:Aufgabe_Energie_für_Mensch_und_Tier.png|435px|left]] | ||
| + | '''5) Energie für den Menschen''' | ||
| + | |||
| + | Mit welchen Energieträgern bekommen der Mensch, eine Kuh, eine Graspflanze und eine Weizenpflanze ihre Energie? In welche Träger wird die Energie hineingesteckt? | ||
| + | '''a)''' Trage die Begriffe in die Diagramme unter die Pfeile ein! | ||
| + | Körner/Fleisch Körner | ||
| + | Muskelmasse&Fett&Milch Muskelmasse&Fett&Milch | ||
| + | Kot&Urin Kot&Urin | ||
| + | Wärme Wärme | ||
| + | Grashalme Grashalme | ||
| + | Bewegung Bewegung | ||
| + | Licht Licht | ||
| − | ''' | + | '''b)''' Zeichne eine Energieumladerkette für einen Menschen, der nur Fleisch isst und einen Menschen, der nur Brot ist. Wo kommt schlußendlich die Energie für den Menschen her? |
| − | + | <br style="clear: both" /> | |
| − | + | ||
| − | ''' | + | '''6) Viele verschiedene Energieumlader''' |
| − | + | ||
| − | + | ||
| + | In [[Media: Energieumlader-Tabelle_teilausgefüllt_als_Aufgabe.pdf|dieser Tabelle]] sind viele Energieumlader aufgeführt. Auf der linken Seite sieht man, mit welchem Träger sie ihre Energie bekommen und oben kann man ablesen, mit welchem Träger sie die Energie wieder abgeben. Ein Baum bekommt seine Energie mit dem Licht und speichert sie in seinem Holz. Ein Ofen wiederum kann seine Energie mit Holz bekommen und sie mit der warmen Luft wieder abgeben. | ||
| − | + | *Ergänze die farbig markierten Lücken mit geeigneten Energieumladern. | |
==Fußnoten== | ==Fußnoten== | ||
| − | <references | + | <references> |
Aktuelle Version vom 31. Dezember 2025, 15:13 Uhr
Aufgaben zur Energie
Energieträger und Energieformen
1) Eine Batterie ist ein Energieträger. Denn in der Batterie steckt Energie, mit der man einen Motor antreiben kann.
- Nenne drei weitere Gegenstände, die auch Energieträger sind und sage, was man mit dieser Energie machen kann.
2) Die Tabelle zeigt, welche verschiedenen Namen man der Energie verschiedener Träger gegeben hat.
- Nenne für jede Energieform ein anderes Beispiel in folgender Art:
- "Der Wind, also Luft, die sich schnell bewegt, enthält Bewegungsenergie."
|
Energieträger |
Name der Energieform | |
|---|---|---|
|
Holz |
chemische Energie | |
|
heißes Wasser |
Wärmeenergie | |
|
geriebener Luftballon |
elektrische Energie | |
|
Licht |
Lichtenergie[1] | |
|
laufender Mensch |
Bewegungsenergie | mechanische Energie |
| Spannenergie | ||
|
hochgelegenes Wasser in einem Stausee |
Lageenergie | |
3) Aus der Tabelle kann man ablesen:
- "Mit der Energie von 38 Stunden Sonnenlicht auf einen Quadratmeter kann man den Akku eines E-Autos aufladen."
- Bilde drei weitere Sätze in dieser Art.
|
Gegenstand |
Energiemenge in Joule |
|---|---|
|
Sonnenlicht auf einen m2 für eine Sekunde |
1.300 J |
|
ein Liter Benzin |
30.000.000 J |
|
Akku eines E-Autos[2] |
180.000.000 J |
|
aufgepumpter Fahrradreifen |
600 J |
|
Schulranzen auf einem ein Meter hohen Tisch |
100 J |
|
Ein Liter kochendes Wasser[3] |
300.000 J |
|
Fahrradfahrerin mit 30 km/h |
3.000 J |
|
eine Tafel Schokolade |
2.000.000 J |
Energiewandler / Energieumlader
4) Energie für Maschinen
Ein Automotor bekommt mit dem Benzin seine Energie und setzt damit das Auto in Bewegung. Der Motor wird dabei auch sehr heiss. Der Motor lädt die Energie vom Benzin auf die Bewegung des Autos und auf den heissen Motor um.
- a) Trage in die Energieumladerdiagramme die passenden Energieträger oder den Namen des Umladers ein!
- b) Wie kann man Energie von Licht auf Bewegung umladen? Zeichne dazu zwei geeignete Energieumlader hintereinander.
5) Energie für den Menschen
Mit welchen Energieträgern bekommen der Mensch, eine Kuh, eine Graspflanze und eine Weizenpflanze ihre Energie? In welche Träger wird die Energie hineingesteckt? a) Trage die Begriffe in die Diagramme unter die Pfeile ein!
Körner/Fleisch Körner Muskelmasse&Fett&Milch Muskelmasse&Fett&Milch Kot&Urin Kot&Urin Wärme Wärme Grashalme Grashalme Bewegung Bewegung Licht Licht
b) Zeichne eine Energieumladerkette für einen Menschen, der nur Fleisch isst und einen Menschen, der nur Brot ist. Wo kommt schlußendlich die Energie für den Menschen her?
6) Viele verschiedene Energieumlader
In dieser Tabelle sind viele Energieumlader aufgeführt. Auf der linken Seite sieht man, mit welchem Träger sie ihre Energie bekommen und oben kann man ablesen, mit welchem Träger sie die Energie wieder abgeben. Ein Baum bekommt seine Energie mit dem Licht und speichert sie in seinem Holz. Ein Ofen wiederum kann seine Energie mit Holz bekommen und sie mit der warmen Luft wieder abgeben.
- Ergänze die farbig markierten Lücken mit geeigneten Energieumladern.
Fußnoten
- ↑ Das Licht selbst besteht nicht aus Energie, es enthält die Energie! Was das Licht selbst ist, kann man nicht so einfach beantworten.
- ↑ Siehe Wikipedia: Tesla Model 3
- ↑ Im Vergleich zu Zimmertemperatur bei 20°C.