Untersuchung von Schwingungen mit der Differentialgleichung: Unterschied zwischen den Versionen
(→Differentialgleichung) |
(→Differentialgleichung) |
||
| (Eine dazwischenliegende Version des gleichen Benutzers werden nicht angezeigt) | |||
| Zeile 73: | Zeile 73: | ||
\end{alignat} | \end{alignat} | ||
</math> | </math> | ||
| − | Das Ergebnis hängt nicht mehr von der Masse ab! Das bedeutet, dass auch die Bewegung des Fadenpendels von der Masse unabhängig ist, was die [[Praktikum: Untersuchung eines Fadenpendels|Messungen am Fadenpendel]] bestätigt. | + | Das Ergebnis hängt nicht mehr von der Masse ab! Das bedeutet, dass auch die Bewegung des Fadenpendels von der Masse unabhängig ist, was die [[Praktikum: Untersuchung eines Fadenpendels|Messungen am Fadenpendel]] bestätigt. Die Periodendauer, bzw. die Frequenz ist also unabhängig von der Masse des schwingenden Gegenstandes, weil bei größerer Masse die Rückstellkraft und die Trägheit in gleichem Maße zunehmen. |
Eine exakte Lösung der DGL ist mit elementaren Funktionen nicht möglich. Man kann aber nährungsweise durch geschicktes Probieren mit dem Computer eine "numerische Lösung" finden. | Eine exakte Lösung der DGL ist mit elementaren Funktionen nicht möglich. Man kann aber nährungsweise durch geschicktes Probieren mit dem Computer eine "numerische Lösung" finden. | ||
(Vgl. [http://de.wikipedia.org/wiki/Mathematisches_Pendel Wikipedia] oder die [http://mikomma.de/mech/kpendel/pendel_exakt.html Berechnungen von Michael Komma]) | (Vgl. [http://de.wikipedia.org/wiki/Mathematisches_Pendel Wikipedia] oder die [http://mikomma.de/mech/kpendel/pendel_exakt.html Berechnungen von Michael Komma]) | ||
| − | Für die lineare Näherung ergibt sich die DGL einer harmonischen Schwingung: | + | Für die lineare Näherung bei kleinen Auslenkungen ergibt sich die DGL einer harmonischen Schwingung: |
:<math>\ddot y = - \frac{D}{m}\,y = - \frac{m\, g}{l\, m}\, y = - \frac{g}{l}\, y</math> | :<math>\ddot y = - \frac{D}{m}\,y = - \frac{m\, g}{l\, m}\, y = - \frac{g}{l}\, y</math> | ||
und die bekannten Lösungen | und die bekannten Lösungen | ||
:<math>y(t) = \hat y \, \sin(\omega \, t)\quad \text{mit} \quad \omega ^2 = \frac{D}{m}=\frac{g}{l}</math> | :<math>y(t) = \hat y \, \sin(\omega \, t)\quad \text{mit} \quad \omega ^2 = \frac{D}{m}=\frac{g}{l}</math> | ||
| − | |||
| − | |||
==Federpendel im Gravitationsfeld== | ==Federpendel im Gravitationsfeld== | ||
Aktuelle Version vom 21. Oktober 2021, 17:15 Uhr
(Kursstufe > Mechanische Schwingungen)
Inhaltsverzeichnis
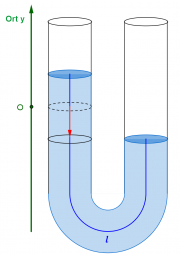
Schwingende Flüssigkeit im U-Rohr
Animation
Mit Hilfe dieser Animation kann man, auch ohne sich die Finger nass zu machen, Wasser in einem U-Rohr schwingen lassen.
Koordinatensystem
Den Ort der Flüssigkeit kann man durch die Lage eines Wasserspiegels beschreiben. Dabei sind Auslenkungen nach oben positiv und der Koordinatenursprung ist in der Ruhelage.
Kraftverlauf
Die Rückstellkraft entspricht der Gewichtskraft der Wassermenge, die sich über dem tieferen Wasserspiegel befindet. Die Masse läßt sich über das Volumen [math]V[/math] und die Dichte [math]\varrho[/math] der Flüssigkeit bestimmen. Das Volumen über die Querschnittsfläche [math]A[/math] und die Höhe [math]2\, y[/math]. Dabei ist die Höhe gerade die doppelte Auslenkung der Wassersäule!
- [math]F = - m_y\, g = -\, V\, \varrho \, g = -\, A\, 2\, y\, \varrho \, g = -(2\, A\, \varrho \, g)\, y[/math]
Die Rückstellkraft ist also proportional zur Auslenkung, die Schwingung ist harmonisch!
DGL
Der Proportionalitätsfaktor [math]2\, A\, \varrho \, g[/math] entspricht der Federkonstanten [math]D[/math]. Daraus folgt direkt die Differentialgleichung und deren Lösung:
- [math]m\, \ddot y = - D \, y \quad \Leftrightarrow \quad \ddot y = -\frac{D}{m} \, y \qquad \text{mit} \quad D = 2\, A\, \varrho \, g[/math]
- [math]y(t)=\hat y \, \sin(\omega \, t) \qquad \text{mit} \quad \omega^2 = \frac{D}{m}[/math]
Dabei ist [math]m[/math] die Masse der gesamten Flüssigkeit.
Es sieht also zunächst so aus, als ob die Frequenz von der Dichte der Flüssigkeit und auch von der Dicke des Rohres abhängt. Aber die Masse der schwingenden Flüssigkeit hängt auch von der Querschnittsfläche und von der Dichte ab! Man kann die Form der Flüssigkeit als einen "gebogenen Zylinder" ansehen, der tatsächlich das gleiche Volumen hat wie der gerade Zylinder.[1] Die Länge des Zylinders wird [math]l[/math] genannt:
- [math]\omega^2 = \frac{D}{m} = \frac{2\, A\, \varrho \, g}{V\, \varrho } = \frac{2\, A \, g}{ V } = \frac{2\, g}{l}[/math]
Die Frequenz hängt also nicht von der Masse oder der Dichte der schwingenden Flüssigkeit ab!
Die Unabhängigkeit von der Masse kann man auch gut durch eine fiktive Teilung des U-Rohrs einsehen: Denkt man sich das Rohr parallel zur Zeichenebene halbiert, so erhält man zwei U-Rohre mit halbkreisförmigen Querschnitt. In jeder dieser Hälften schwingt die Flüssigkeit so wie vorher!
Das Fadenpendel
Animation
Anhand dieser Animation kann man die Rückstellkraft beim Fadenpendel untersuchen.
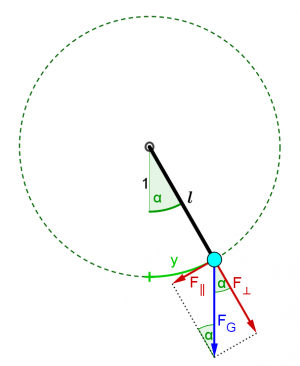
Koordinatensystem
Am geeignetsten ist ein gebogenes System, das genau dem Weg des Pendelkörpers folgt. Den Ort gibt man daher mit der Länge eines Kreisbogens an. Die Ruhelage ist der Ursprung und Ausschläge nach rechts sind positiv.
Der Ort auf dem Kreis hängt direkt mit dem Winkel (im Bogenmaß) zusammen:
- [math]y = l\, \alpha\quad \Leftrightarrow \quad \alpha= \frac{y}{l}[/math]
Kraftverlauf
Die Rückstellkraft kommt durch die Gewichtskraft des Pendelkörpers zustande. Sie muss parallel zur Bewegungsrichtung wirken, das heißt die Rückstellkraft ist der zur Bewegungsrichtung parallele Anteil der Gewichtskraft:
- [math]F(y) = - \, F_g \, \sin(\alpha) = - \, m\, g \, \sin(\frac{y}{l})[/math]
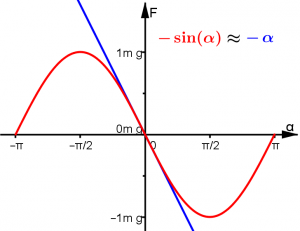
Die Rückstellkraft ist also nicht proportional zur Auslenkung und die Schwingung ist nicht harmonisch![2] An der graphischen Darstellung des Kraftverlaufs sieht man gut, dass man bei einem Winkel von 90° die maximale Rückstellkraft, nämlich gerade die gesamte Gewichtskraft erreicht hat. Für Werte über 90°, die man mit einer Stange als Befestigung auch erreichen kann, nimmt die Rückstellkraft dann für größere Winkel wieder ab.
Man kann den Kraftverlauf für kleine Ausschläge linear nähern, indem man die Sinuskurve durch die Tangente an der Stelle [math]y=0[/math] ersetzt. Das nennt man auch "Kleinwinkelnäherung". Die Steigung beträgt dort:
- [math]F'(y)= - \, m\, g \, \frac{1}{l}\, \cos(\frac{y}{l})\quad \Rightarrow \quad F'(0) = - \, m\, g \, \frac{1}{l}[/math]
Demnach gilt für den Kraftverlauf bei kleinen Amplituden ungefähr:
- [math]F(y)\approx - \, m \, g \, \frac{y}{l} = - \, \frac{m \, g}{l} \, y[/math]
Bemerkenswert ist, dass die Steigung der Kraftkurve, also die "Federkonstante" proportional zur Masse ist. Bei der doppelten Masse ist also die Federkonstante auch doppelt so groß.
Differentialgleichung
Für die DGL setzt man die oben berechnete Rückstellkraft gleich mit der beschleunigenden Kraft:
- [math] \begin{alignat}{2} m \, \ddot y&= - \, m\, g \, \sin(\frac{y}{l}) & \quad | :m \\ \Rightarrow \quad \ddot y&= - \, g \, \sin(\frac{y}{l}) \end{alignat} [/math]
Das Ergebnis hängt nicht mehr von der Masse ab! Das bedeutet, dass auch die Bewegung des Fadenpendels von der Masse unabhängig ist, was die Messungen am Fadenpendel bestätigt. Die Periodendauer, bzw. die Frequenz ist also unabhängig von der Masse des schwingenden Gegenstandes, weil bei größerer Masse die Rückstellkraft und die Trägheit in gleichem Maße zunehmen.
Eine exakte Lösung der DGL ist mit elementaren Funktionen nicht möglich. Man kann aber nährungsweise durch geschicktes Probieren mit dem Computer eine "numerische Lösung" finden. (Vgl. Wikipedia oder die Berechnungen von Michael Komma)
Für die lineare Näherung bei kleinen Auslenkungen ergibt sich die DGL einer harmonischen Schwingung:
- [math]\ddot y = - \frac{D}{m}\,y = - \frac{m\, g}{l\, m}\, y = - \frac{g}{l}\, y[/math]
und die bekannten Lösungen
- [math]y(t) = \hat y \, \sin(\omega \, t)\quad \text{mit} \quad \omega ^2 = \frac{D}{m}=\frac{g}{l}[/math]
Federpendel im Gravitationsfeld
Koordinatensystem
Zur Übung und aus Interesse oder zur tieferen Einsicht gibt es zwei Varianten:
A Das untere Ende der entspannten Feder ist der Koordinatenursprung und das Koordinatensystem zeigt nach oben.
B Die Ruhelage der Schwingung ist der Koordinatenursprung.
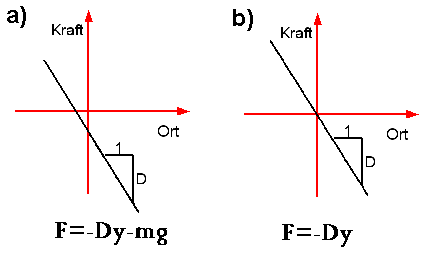
Kraftverlauf
A Bei einer Verlängerung der Feder um die Länge [math]y[/math] wirken die Gewichtskraft und die Federkraft auf den Gegenstand. Die Gewichtskraft nach unten und die Federkraft nach oben. (Durch die negative Auslenkung [math]y[/math] ist [math]- D \, y[/math] positiv!)
Die Ruhelage, bei sich die Gewichtskraft und die Federkraft gerade ausgleichen (die "Nullstelle" des Graphen), liegt nicht im Koordinatenursprung.
- [math]F(y) = F_f - F_g = - D\, y - m\, g[/math]
Der Kraftverlauf ist also linear, aber nicht proportional zur Auslenkung.
B In diesem Fall verschwindet die Kraftwirkung gerade bei [math]y=0\,\rm m[/math]. Das Koordinatensystem ist entsprechend verschoben und der Kraftverlauf vereinfacht sich zu:
- [math]F(y) = -D \, y[/math]
Differentialgleichung
A Aus dem Kraftverlauf ergibt sich:
- [math]m\, \ddot y = - D\, y - m\, g \quad \Leftrightarrow \quad \ddot y = -\frac{D}{m} y -g[/math]
Das ist einleuchtend. Zusätzlich zur Beschleunigung durch die Feder, die vom Ort abhängt, kommt noch eine konstante Erdbeschleunigung hinzu.
Wenn man die bekannte Lösung der Variante B im Kopf hat, dann kann man sich schon denken was als Lösung bei A herauskommt. Es muss eine sinusförmige Schwingung sein, die nach unten verschoben ist. Die Verschiebung [math]r[/math] entspricht der Verlängerung der Feder durch die Gewichtskraft des Gegenstandes in der Ruhelage. Dort gilt:
- [math]D\, r = m \, g \quad \Rightarrow \quad r = \frac{m \, g}{D}[/math]
Also sollten diese Ortsfunktionen Lösungen sein:
- [math]y(t)= \hat y \, \sin( \omega \, t) - \frac{m\, g}{D}[/math] mit [math]\omega ^2 = \frac{D}{m}[/math]
Das kann man nun nachrechnen. Erstmal wird zweimal abgeleitet:
- [math]\ddot y = -\omega ^2 \, \hat y \sin(\omega \, t)[/math]
Das sollte nun der rechten Seite der DGL entsprechen:
- [math]-\frac{D}{m} \, y -g = -\frac{D}{m} \left( \hat y \, \sin( \omega \, t) - \frac{m\, g}{D} \right) -g = -\frac{D}{m}\, \hat y \, \sin( \omega \, t) + g -g[/math]
Das stimmt also! Die Verschiebung des Kraftverlaufs führt nur zu einer Verschiebung der Schwingung bei gleicher Frequenz.
B Hier ergibt sich das Altbekannte.
Fußnoten
- ↑ Interessanterweise wird der Zylinder beim Biegen auf der Innenseite genausoviel zusammengequetscht wie er auf des Außenseite auseinandergezogen wird. Das liegt an der Proportionalität von Radius und Umfang. (Vgl. Wikipedia:Torusvolumen)
- ↑ Durch einen "Trick" kann man aber immerhin erreichen, dass die Schwingungsdauer nicht von der Amplitude abhängt: Bei dem sogenannten "Zykloidenpendel" wird die Fadenlänge immer kürzer, je größer die Elongation ist. Die Rückstellkraft ist aber nach wie vor nicht proportional zur Auslenkung.