Zusammenfassung Kinematik: Unterschied zwischen den Versionen
| (10 dazwischenliegende Versionen des gleichen Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | ([[Inhalt_Klasse_10|'''Klassische Mechanik''']] > [[Inhalt_Klasse_10#Kinematik_-_.22Ja.2C_wo_laufen_sie_denn.3F.22|'''Kinematik''']]) | ||
| + | |||
| + | ([[Inhalt_Kursstufe|'''Kursstufe''']] > [[Inhalt_Kursstufe#Mechanik|''' Mechanik''']]) | ||
| + | |||
Um die Bewegung eines Körpers zu beschreiben vereinfacht man die Situation stark. | Um die Bewegung eines Körpers zu beschreiben vereinfacht man die Situation stark. | ||
Oft betrachtet man einen Gegenstand auf einen Punkt, den Schwerpunkt konzentriert. | Oft betrachtet man einen Gegenstand auf einen Punkt, den Schwerpunkt konzentriert. | ||
| − | Meistens werden auch alle Rotationen des Körpers | + | Meistens werden auch alle Rotationen des Körpers vernachlässigt und nur Translationen im Raum betrachtet. |
| − | + | ||
| − | + | ||
== Beschreibung einer Situation == | == Beschreibung einer Situation == | ||
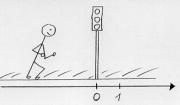
| − | [[Image: | + | [[Image:Mechanik_Koordinatensystem_geradlinig.jpg|thumb|Die Ampel dient als Koordinatenursprung]] |
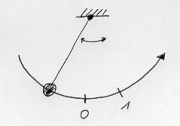
| − | + | [[Image:Mechanik_Koordinatensystem_gebogen.jpg|thumb|Gebogenes Koordinatensystem für ein Fadenpendel]] | |
| − | + | ||
| − | + | ||
| − | Die Ampel dient als Koordinatenursprung | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | [[Image: | + | |
| − | + | ||
| − | Gebogenes Koordinatensystem für ein Fadenpendel | + | |
| − | + | ||
| − | + | ||
=== Wo ist der Körper? === | === Wo ist der Körper? === | ||
| − | Zur genaueren Beschreibung muss man ein Koordinatensystem festlegen. Dies kann geradlinig oder auch gebogen sein, wie im Falle eines Fadenpendels. Bei vielen Fällen reicht ein eindimensionales Koordinatensystem, bei dem sich der Körper nur nach vorne und hinten bewegen kann, aus. Mit einem negativen Vorzeichen wird eine Position vor dem Ursprung angegeben. | + | Zur genaueren Beschreibung einer Bewegung muss man ein Orts-Koordinatensystem festlegen. Dies kann geradlinig oder auch gebogen sein, wie im Falle eines Fadenpendels. Bei vielen Fällen reicht ein eindimensionales Koordinatensystem, bei dem sich der Körper nur nach vorne und hinten bewegen kann, aus. Mit einem negativen Vorzeichen wird eine Position vor dem Ursprung angegeben. |
| − | Das Koordinatensystem kann aber auch zwei- oder dreidimensional sein. Bei Bewegungen in der Fläche oder im Raum ist der Ort eine vektorielle Größe, die man als | + | Das Koordinatensystem kann aber auch zwei- oder dreidimensional sein. Bei Bewegungen in der Fläche oder im Raum ist der Ort eine vektorielle Größe, die man als <math>\vec s</math> notiert. |
In diesem Koordinatensystem kann man nun die Position eines festen Punktes des Körpers, häufig des Schwerpunkts S, mit Hilfe von Koordinaten exakt angeben. | In diesem Koordinatensystem kann man nun die Position eines festen Punktes des Körpers, häufig des Schwerpunkts S, mit Hilfe von Koordinaten exakt angeben. | ||
| − | |||
| − | |||
=== Wie schnell ist der Körper? === | === Wie schnell ist der Körper? === | ||
| − | Die Geschwindigkeit ist die zeitliche Änderung des Ortes. ( | + | Die Geschwindigkeit ist die zeitliche Änderung des Ortes. (<math>\dot s</math>) Bei einer eindimensionalen Bewegung wird die Richtung entgegen dem Koordinatensystem mit einem negativen Vorzeichen ausgedrückt. In der Fläche und im Raum ist die Geschwindigkeit eine vektorielle Größe und wird als <math>\vec v</math> notiert. |
| − | + | ||
| − | + | ||
=== Bremst/beschleunigt der Körper? === | === Bremst/beschleunigt der Körper? === | ||
| − | Die Beschleunigung ist die zeitliche Änderung der Geschwindigkeit. | + | Die Beschleunigung ist die zeitliche Änderung der Geschwindigkeit. <math>a = \dot v</math> Im eindimensionalen gibt ein negatives Vorzeichen die Verringerung der Geschwindigkeit, also einen Bremsvorgang an. In der Fläche und im Raum ist sie auch eine vektorielle Größe und wird <math>\vec a</math> geschrieben. |
| − | + | ||
| − | + | ||
== Beschreibung des zeitlichen Verlaufs == | == Beschreibung des zeitlichen Verlaufs == | ||
| − | |||
| − | |||
=== Wann ist der Körper wo? === | === Wann ist der Körper wo? === | ||
| − | Ordnet man jedem Zeitpunkt einem Ort zu, so erhält man das Ortsgesetz | + | Ordnet man jedem Zeitpunkt einem Ort zu, so erhält man das Ortsgesetz <math>s(t)</math> der Bewegung. Das Schaubild dieser Zuordnung ist das Ort-Zeit-Diagramm. |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| + | * Die Steigung einer Tangente des Schaubildes ist die Momentangeschwindigkeit <math>v=\dot s</math> des Körpers, | ||
| + | * die Sekantensteigung ist die mittlere Geschwindigkeit <math>\bar v = \frac{\Delta s}{\Delta t}</math>. | ||
=== Wann ist der Körper wie schnell? === | === Wann ist der Körper wie schnell? === | ||
| − | Ordnet man jedem Zeitpunkt der momentanen Geschwindigkeit zu, so erhält man das Geschwindigkeitsgesetz | + | Ordnet man jedem Zeitpunkt der momentanen Geschwindigkeit zu, so erhält man das Geschwindigkeitsgesetz <math>v(t)</math>. Das Schaubild heißt Geschwindigkeit-Zeit-Diagramm. |
| − | * Die Steigung einer Tangente im Geschwindigkeit-Zeit-Diagramm ist die momentane Beschleunigung | + | * Die Steigung einer Tangente im Geschwindigkeit-Zeit-Diagramm ist die momentane Beschleunigung <math>a=\dot v</math>, |
| − | * die Sekantensteigung ist die mittlere Beschleunigung | + | * die Sekantensteigung ist die mittlere Beschleunigung <math>\bar a= \frac{\Delta v}{\Delta t}</math> |
=== Flächen in Diagrammen === | === Flächen in Diagrammen === | ||
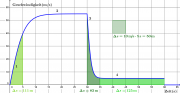
| + | [[Bild:v-t-Diagramm_Fläche_unter_Kurve.png|thumb|Flächen im v-t-Diagramm eines Fallschirmspringers.]] | ||
Die Flächen zwischen dem Schaubild und der Zeitachse lassen sich anschaulich interpretieren. Grundlage dazu ist der sogenannte Hauptsatz der Differential-Integralrechnung (HDI), den man in Worten so formulieren kann: | Die Flächen zwischen dem Schaubild und der Zeitachse lassen sich anschaulich interpretieren. Grundlage dazu ist der sogenannte Hauptsatz der Differential-Integralrechnung (HDI), den man in Worten so formulieren kann: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Das Integral (die Fläche) unterhalb der Änderungsrate ergibt die Gesamtänderung. Dabei werden Flächen unterhalb der x-Achse negativ gewertet. | Das Integral (die Fläche) unterhalb der Änderungsrate ergibt die Gesamtänderung. Dabei werden Flächen unterhalb der x-Achse negativ gewertet. | ||
| − | Trägt man z.B. die zeitliche Änderungsrate | + | Trägt man z.B. die zeitliche Änderungsrate des Ortes (die Geschwindigkeit) über der Zeit auf, so entspricht die Fläche unterhalb des Schaubildes der Gesamtänderung des Ortes. |
| − | + | <math>\Delta s = s(t_2)-s(t_1) = \int_{t_1}^{t_2} v(t) \ \mathrm{dt}</math> | |
| − | Mit Hilfe des GTRs kann man Flächen unter Schaubildern numerisch bestimmen. (Genauere Beschreibung [ | + | Mit Hilfe des GTRs kann man Flächen unter Schaubildern numerisch bestimmen. (Genauere Beschreibung unter [[Energie,_Energieträger_und_Potential - Ein zentrales Modell#Berechnung von Energiemengen|Berechnung von Energiemengen]].) |
| − | + | Für die Beschreibung von Bewegungen bedeutet das: | |
* Die Fläche unterhalb des Geschwindigkeit-Schaubildes entspricht der Ortsänderung, also der zurückgelegten Strecke. | * Die Fläche unterhalb des Geschwindigkeit-Schaubildes entspricht der Ortsänderung, also der zurückgelegten Strecke. | ||
| − | * Die Fläche unterhalb des Beschleunigungs-Schaubildes entspricht der Geschwindigkeitsänderung. | + | * Die Fläche unterhalb des Beschleunigungs-Schaubildes entspricht der Geschwindigkeitsänderung. |
| − | + | ||
| − | + | ||
== Spezielle Bewegungstypen == | == Spezielle Bewegungstypen == | ||
| Zeile 93: | Zeile 67: | ||
der Körper ist zum Zeitpunkt t=0 im Koordinatenursprung: | der Körper ist zum Zeitpunkt t=0 im Koordinatenursprung: | ||
| − | + | <math>s(t)=v t, \qquad v(t)=v, \qquad a(t)=0</math>, | |
im allgemeinen Fall: | im allgemeinen Fall: | ||
| − | + | <math>s(t)=v t + s(0), \qquad v(t)=v, \qquad a(t)=0</math>, | |
| Zeile 108: | Zeile 82: | ||
der Körper ist zum Zeitpunkt t=0 im Koordinatenursprung und in Ruhe: | der Körper ist zum Zeitpunkt t=0 im Koordinatenursprung und in Ruhe: | ||
| − | + | <math>s(t)=\frac{1}{2} a t^2, \qquad v(t)= a t, \qquad a(t)=a</math>, | |
im allgemeinen Fall: | im allgemeinen Fall: | ||
| − | + | <math>s(t)=\frac{1}{2} a t^2 + v(0) t + s(0), \qquad v(t)= a t + v(0) t, \qquad a(t)=a</math>, | |
| − | + | ||
== Überlagerung und Zerlegung von Bewegungen == | == Überlagerung und Zerlegung von Bewegungen == | ||
Vektoraddition von Geschwindigkeiten | Vektoraddition von Geschwindigkeiten | ||
| − | |||
* [http://www.surendranath.org/Applets/Kinematics/BoatRiver/BoatRiverApplet.html Applet mit einem Boot, das einen Fluss überquert. (B. Surendranath)] | * [http://www.surendranath.org/Applets/Kinematics/BoatRiver/BoatRiverApplet.html Applet mit einem Boot, das einen Fluss überquert. (B. Surendranath)] | ||
Zerlegung von mehrdimensionalen Bewegungen | Zerlegung von mehrdimensionalen Bewegungen | ||
| − | + | *[[Animation: Schiefer Wurf| Der waagrechte oder schiefe Wurf als Animation.]] | |
| − | * [ | + | |
| − | + | ||
== Verschiedene Bezugssyteme == | == Verschiedene Bezugssyteme == | ||
Relativität | Relativität | ||
| − | + | * [http://www.physics.ucla.edu/demoweb/ntnujava/relativeVelocity/relativeVelocity.html Relative Sichtweisen der gleichen Bewegungen auf einem Fluss.] | |
| − | * [http://www.physics.ucla.edu/demoweb/ntnujava/relativeVelocity/relativeVelocity.html Relative Sichtweisen der gleichen Bewegungen auf einem Fluss.] | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
Aktuelle Version vom 20. April 2018, 04:49 Uhr
(Klassische Mechanik > Kinematik)
Um die Bewegung eines Körpers zu beschreiben vereinfacht man die Situation stark.
Oft betrachtet man einen Gegenstand auf einen Punkt, den Schwerpunkt konzentriert.
Meistens werden auch alle Rotationen des Körpers vernachlässigt und nur Translationen im Raum betrachtet.
Inhaltsverzeichnis
Beschreibung einer Situation
Wo ist der Körper?
Zur genaueren Beschreibung einer Bewegung muss man ein Orts-Koordinatensystem festlegen. Dies kann geradlinig oder auch gebogen sein, wie im Falle eines Fadenpendels. Bei vielen Fällen reicht ein eindimensionales Koordinatensystem, bei dem sich der Körper nur nach vorne und hinten bewegen kann, aus. Mit einem negativen Vorzeichen wird eine Position vor dem Ursprung angegeben.
Das Koordinatensystem kann aber auch zwei- oder dreidimensional sein. Bei Bewegungen in der Fläche oder im Raum ist der Ort eine vektorielle Größe, die man als [math]\vec s[/math] notiert.
In diesem Koordinatensystem kann man nun die Position eines festen Punktes des Körpers, häufig des Schwerpunkts S, mit Hilfe von Koordinaten exakt angeben.
Wie schnell ist der Körper?
Die Geschwindigkeit ist die zeitliche Änderung des Ortes. ([math]\dot s[/math]) Bei einer eindimensionalen Bewegung wird die Richtung entgegen dem Koordinatensystem mit einem negativen Vorzeichen ausgedrückt. In der Fläche und im Raum ist die Geschwindigkeit eine vektorielle Größe und wird als [math]\vec v[/math] notiert.
Bremst/beschleunigt der Körper?
Die Beschleunigung ist die zeitliche Änderung der Geschwindigkeit. [math]a = \dot v[/math] Im eindimensionalen gibt ein negatives Vorzeichen die Verringerung der Geschwindigkeit, also einen Bremsvorgang an. In der Fläche und im Raum ist sie auch eine vektorielle Größe und wird [math]\vec a[/math] geschrieben.
Beschreibung des zeitlichen Verlaufs
Wann ist der Körper wo?
Ordnet man jedem Zeitpunkt einem Ort zu, so erhält man das Ortsgesetz [math]s(t)[/math] der Bewegung. Das Schaubild dieser Zuordnung ist das Ort-Zeit-Diagramm.
- Die Steigung einer Tangente des Schaubildes ist die Momentangeschwindigkeit [math]v=\dot s[/math] des Körpers,
- die Sekantensteigung ist die mittlere Geschwindigkeit [math]\bar v = \frac{\Delta s}{\Delta t}[/math].
Wann ist der Körper wie schnell?
Ordnet man jedem Zeitpunkt der momentanen Geschwindigkeit zu, so erhält man das Geschwindigkeitsgesetz [math]v(t)[/math]. Das Schaubild heißt Geschwindigkeit-Zeit-Diagramm.
- Die Steigung einer Tangente im Geschwindigkeit-Zeit-Diagramm ist die momentane Beschleunigung [math]a=\dot v[/math],
- die Sekantensteigung ist die mittlere Beschleunigung [math]\bar a= \frac{\Delta v}{\Delta t}[/math]
Flächen in Diagrammen
Die Flächen zwischen dem Schaubild und der Zeitachse lassen sich anschaulich interpretieren. Grundlage dazu ist der sogenannte Hauptsatz der Differential-Integralrechnung (HDI), den man in Worten so formulieren kann:
Das Integral (die Fläche) unterhalb der Änderungsrate ergibt die Gesamtänderung. Dabei werden Flächen unterhalb der x-Achse negativ gewertet.
Trägt man z.B. die zeitliche Änderungsrate des Ortes (die Geschwindigkeit) über der Zeit auf, so entspricht die Fläche unterhalb des Schaubildes der Gesamtänderung des Ortes.
[math]\Delta s = s(t_2)-s(t_1) = \int_{t_1}^{t_2} v(t) \ \mathrm{dt}[/math]
Mit Hilfe des GTRs kann man Flächen unter Schaubildern numerisch bestimmen. (Genauere Beschreibung unter Berechnung von Energiemengen.)
Für die Beschreibung von Bewegungen bedeutet das:
- Die Fläche unterhalb des Geschwindigkeit-Schaubildes entspricht der Ortsänderung, also der zurückgelegten Strecke.
- Die Fläche unterhalb des Beschleunigungs-Schaubildes entspricht der Geschwindigkeitsänderung.
Spezielle Bewegungstypen
Die Gleichförmige Bewegung
- Hierbei bewegt sich ein Körper mit konstanter Geschwindigkeit, der Ort ändert sich gleichmäßig.
- Im Ort-Zeit-Diagramm ist das Schaubild eine (Ursprungs-)Gerade.
- Die Bewegunggesetze sind:
der Körper ist zum Zeitpunkt t=0 im Koordinatenursprung:
[math]s(t)=v t, \qquad v(t)=v, \qquad a(t)=0[/math],
im allgemeinen Fall:
[math]s(t)=v t + s(0), \qquad v(t)=v, \qquad a(t)=0[/math],
Die gleichmäßig beschleunigte Bewegung
- Hierbei ist die Beschleunigung konstant, die Geschwindigkeit nimmt gleichmäßig zu oder ab.
- Im Ort-Zeit-Diagramm ist das Schaubild eine Parabel.
- Die Bewegungsgesetze sind:
der Körper ist zum Zeitpunkt t=0 im Koordinatenursprung und in Ruhe:
[math]s(t)=\frac{1}{2} a t^2, \qquad v(t)= a t, \qquad a(t)=a[/math],
im allgemeinen Fall:
[math]s(t)=\frac{1}{2} a t^2 + v(0) t + s(0), \qquad v(t)= a t + v(0) t, \qquad a(t)=a[/math],
Überlagerung und Zerlegung von Bewegungen
Vektoraddition von Geschwindigkeiten
Zerlegung von mehrdimensionalen Bewegungen
Verschiedene Bezugssyteme
Relativität