Energieübertragung durch Induktion: Lenzsche Regel und Wirbelströme: Unterschied zwischen den Versionen
(→Versuche) |
(→Supraleitung: Stromfluss ohne Energieverlust) |
||
| (30 dazwischenliegende Versionen des gleichen Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | ([[Inhalt_Kursstufe|'''Kursstufe''']] > [[Inhalt_Kursstufe#Elektro-Magnetismus|'''Elektro-Magnetismus''']]) | ||
| + | |||
| + | |||
Die Wirkung der Induktion ist so gerichtet, dass sie der Ursache der Induktion entgegenwirkt. ("Lenzsche Regel") | Die Wirkung der Induktion ist so gerichtet, dass sie der Ursache der Induktion entgegenwirkt. ("Lenzsche Regel") | ||
*Wenn der magnetische Fluss durch eine Spule zunimmt (abnimmt), so fließt der induzierte Strom so durch die Spule, dass das dadurch entstandene Magnetfeld entgegengerichtet (gleichgerichtet) ist und somit versucht den magnetischen Fluss aufrecht zu erhalten. | *Wenn der magnetische Fluss durch eine Spule zunimmt (abnimmt), so fließt der induzierte Strom so durch die Spule, dass das dadurch entstandene Magnetfeld entgegengerichtet (gleichgerichtet) ist und somit versucht den magnetischen Fluss aufrecht zu erhalten. | ||
*Wenn der Stromfluss durch eine Spule sich vergrößert (verkleinert), so wird eine Spannung induziert, die den Stromfluss hemmt (verstärkt) und somit versucht die Stromstärke aufrecht zu erhalten. | *Wenn der Stromfluss durch eine Spule sich vergrößert (verkleinert), so wird eine Spannung induziert, die den Stromfluss hemmt (verstärkt) und somit versucht die Stromstärke aufrecht zu erhalten. | ||
| − | *Wenn durch eine Bewegung eines Magneten sich in einem leitenden Material der magnetische Fluss ändert, so wird durch den induzierten Strom ein Magnetfeld erzeugt, dass die Bewegung des | + | *Wenn durch eine Bewegung eines Magneten sich in einem leitenden Material der magnetische Fluss ändert, so wird durch den induzierten Strom ein Magnetfeld erzeugt, dass die Bewegung des Magneten bremst. |
Die Lenzsche Regel ist ein Spezialfall der Energieerhaltung. Das erkennt man, wenn man annimmt, die Wirkung der Induktion wäre anders gerichtet. | Die Lenzsche Regel ist ein Spezialfall der Energieerhaltung. Das erkennt man, wenn man annimmt, die Wirkung der Induktion wäre anders gerichtet. | ||
| Zeile 8: | Zeile 11: | ||
*Durch eine Zunahme der Stromstärke würde die Stromstärke weiter ansteigen und beliebig groß werden. | *Durch eine Zunahme der Stromstärke würde die Stromstärke weiter ansteigen und beliebig groß werden. | ||
*Durch eine Zunahme der Geschwindigkeit würde sie noch größer und beliebig groß. | *Durch eine Zunahme der Geschwindigkeit würde sie noch größer und beliebig groß. | ||
| − | Um | + | In allen Fällen hätte man ein Perpetuum mobile, das ständig aus dem Nichts Energie erzeugen würde. |
| + | |||
| + | Um der Lenzschen Regel im Induktionsgesetz Rechnung zu tragen, setzt man ein Minuszeichen vor die Induktionsspannung: | ||
:<math>U=-\dot\Phi</math> | :<math>U=-\dot\Phi</math> | ||
| Zeile 15: | Zeile 20: | ||
* Bewegung im Feld bewirkt einen Strom | * Bewegung im Feld bewirkt einen Strom | ||
* Dieser Strom fließt in einem Feld und es wirkt wiederum eine Kraft | * Dieser Strom fließt in einem Feld und es wirkt wiederum eine Kraft | ||
| − | |||
==Versuche== | ==Versuche== | ||
===Schwingender Magnet=== | ===Schwingender Magnet=== | ||
| − | [[Datei:Versuchsaufbau_Lenzsche_Regel.jpg|thumb]] | + | [[Datei:Versuchsaufbau_Lenzsche_Regel.jpg|thumb|hochkant]] |
| − | <br style="clear: both" /> | + | ;Aufbau |
| + | Aus einem Stabmagnet und einer Feder baut man ein Federpendel. Eine Spule mit ca. 500 Windungen wird so platziert, dass ein Pol des Magneten innerhalb der Spule schwingt. | ||
| + | *Man schubst zunächst das Federpendel an und | ||
| + | *verbindet nach einigen Sekunden Anfang und Ende der Spule mit einem Kabel. | ||
| + | ;Beobachtung | ||
| + | *Der Magnet schwingt zunächst mit einer relativ konstanten Amplitude, | ||
| + | *nach dem Anbringen des Kabels nimmt die Amplitude relativ schnell ab und der Magnet kommt zum Stehen. | ||
| + | <br style="clear: both" /> | ||
| + | |||
| + | ;Folgerung | ||
| + | {| | ||
| + | |style="vertical-align:top;"| | ||
| + | Offensichtlich kann die geschlossene Spule der Schwingung Energie entziehen, was bei geöffneter Spule nicht gelingt. | ||
| + | <br>Bewegt sich der Magnet auf die Spule zu oder von ihr weg, so vergrößert oder verkleinert sich der magnetische Fluß durch die Spule. Daher wird eine Spannung in die Spule induziert. Solange aber Anfang und Ende der Spule nicht verbunden sind, gibt es keinen Stromkreis und es fließt nur ein minimaler Strom, der innerhalb der Spule durch die Ladungsverschiebung die Spannung aufbaut. | ||
| + | <br>Ist die Spule geschlossen, so wird durch die Induktionsspannung ein Strom angetrieben. Die dazu nötige Energie kommt aus der Bewegungsenergie (und der Lageenergie) des Magneten. Durch den ohmschen Widerstand der Kupferkabel der Spule wird "der Strom gebremst", oder, besser gesagt, die Energie zur Erwärmung des Kabels verwendet. | ||
| + | <br>Der bewegte Magnet heizt also die Spule auf. | ||
| + | | | ||
| + | Am blauen Punkt kann man den Magneten bewegen. | ||
| + | <br>Dargestellt sind die [[Das_Induktionsgesetz_und_die_magnetische_Flussdichte#Die_magnetische_Flussdichte|Flußdichtelinien]] des Magneten | ||
| + | {{#widget:Iframe | ||
| + | |url=https://www.geogebra.org/material/iframe/id/gsgCytQD/width/629/height/909/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/false/rc/false/ld/false/sdz/false/ctl/false | ||
| + | |width=315 | ||
| + | |height=454 | ||
| + | |border=0 | ||
| + | }} | ||
| + | |} | ||
| + | <br style="clear: both" /> | ||
===Der Fahrraddynamo=== | ===Der Fahrraddynamo=== | ||
| − | + | ;Aufbau | |
| + | Man benötigt ein Fahrrad mit einem Nabendynamo am Vorderrad. | ||
| + | Man hebt das Vorderrad des Fahrrades an und schubst den Vorderreifen an. Dann wartet man ab. | ||
| − | + | Das macht man einmal mit ausgeschaltetem Licht. Dann schaltet man während sich das Rad dreht, das Licht an. | |
| + | ;Beobachtung | ||
| + | Schaltet man das Licht ein, wird das Rad merklich langsamer und bleibt schneller stehen. | ||
| + | ;Erklärung | ||
| + | Durch das Anschubsen wird Energie in die Drehbewegung des Rades übertragen. Bei ausgeschaltetem Licht geht die Bewegungsenergie durch die Reibung im Lager und an der Luft aus dem Rad, wodurch das Lager und die Luft leicht erwärmt werden. (Das müßte man nachmessen, ist aber nicht leicht.) | ||
| + | |||
| + | Schaltet man das Licht ein, wird für den Betrieb der Lampe viel Energie benötigt, die aus dem drehenden Rad kommt. Das Rad wird daher schneller abgebremst. | ||
| + | <br style="clear: both" /> | ||
===Der Kurbel-Generator (Dynamot)=== | ===Der Kurbel-Generator (Dynamot)=== | ||
[[Datei:Versuchsaufbau_Wirbelstrom_Dynamo.jpg|thumb]] | [[Datei:Versuchsaufbau_Wirbelstrom_Dynamo.jpg|thumb]] | ||
| − | + | ;Aufbau | |
| − | Man dreht den Dynamo, um die Lampe zum Leuchten zu bringen und | + | Man dreht den Dynamo, um die Lampe (6V/30W) zum Leuchten zu bringen und jemand schaltet die Lampe an und aus. (Schließt und öffnet den Stromkreis.) |
| − | <br style="clear: both" /> | + | ;Beobachtung |
| + | Schaltet man die Lampe an, ist es richtig anstrengend die Dynamokurbel zu drehen, schaltet man die Lampe aus, geht es viel leichter. | ||
| + | ;Erklärung | ||
| + | Durch das Kurbeln treibt man den Vorgang an und liefert die dazu nötige Energie. Wird die Lampe angeschaltet, so muß man viel Energie lieren, um sie zu betreiben. Ist die Lampe ausgeschaltet, braucht man nur ein bisschen Energie, um die Reibung innerhalb des Dynamos zu überwinden. Genauso ergeht es auch den Kraftwerken in unserem Stromnetz: werden zur Mittagszeit viele elektrische Geräte eingeschaltet, müssen sie mehr Energie liefern als Nachts, wenn viele Geräte ausgeschaltet sind! | ||
| + | <br style="clear: both" /> | ||
===Der belastete Transformator=== | ===Der belastete Transformator=== | ||
vergrößern | vergrößern | ||
| + | |||
| + | ===Die Induktionskochplatte=== | ||
| + | ;Aufbau | ||
| + | Auf eine Induktonskochplatte wird eine Stück Alufolie gelegt und die Platte eingeschaltet. | ||
| + | |||
| + | Die Kochplatte ist mit Hilfe von 4 Spulen nachgebaut worden. Die Spulen haben 500 Windungen, je 2 sind parallel und diese wieder in Reihe geschaltet und mit der Netzspannung verbunden. An jeder Spule liegt also die halbe Netzspannung an. (Schaltet man alle Spulen parallel, so ist der Effekt zwar größer, aber die Sicherung springt ständig raus :) Die 4 Eisenstangen dienen nur der Stabilisierung der Platte. | ||
| + | |||
| + | Auf die Eisenkerne wird eine Aluplatte gelegt und der Strom eingeschaltet. | ||
| + | ;Beobachtung | ||
| + | {| | ||
| + | | | ||
| + | [[Datei:Induktionskochplatte_Alufolie.jpg|thumb| [[Media:Induktionskochplatte_Alufolie.ogg|Hier]] das Video des Versuchs ]] | ||
| + | | | ||
| + | [[Datei:Induktionskochplatte_Eigenbau.jpg|thumb| [[Media:Induktionskochplatte_Eigenbau.ogg|Hier]] das Video des Versuchs ]] | ||
| + | |} | ||
| + | |||
| + | In diesem [http://www.youtube.com/watch?v=k4xsqw463Hs Video] wird ein Eisenstück per Induktion zum Glühen gebracht. (youtube: "Induction Forge - Show and tell" von "Mark Aspery") | ||
| + | |||
| + | ;Erklärung | ||
| + | [[Datei:Spulen im Induktionskochfeld.jpg|thumb|Die flach gewickelte Spule im Inneren eines Induktionskochfeldes.]] | ||
| + | <br style="clear: both" /> | ||
===Der Katapultring=== | ===Der Katapultring=== | ||
[[Datei:Versuchsaufbau_Lenzsche_Regel_Wirbelstrom_Ring_schiessen.jpg|thumb]] | [[Datei:Versuchsaufbau_Lenzsche_Regel_Wirbelstrom_Ring_schiessen.jpg|thumb]] | ||
| − | <br style="clear: both" /> | + | <br style="clear: both" /> |
===Die Ringschaukel=== | ===Die Ringschaukel=== | ||
| Zeile 64: | Zeile 128: | ||
===Der zähe frei Fall=== | ===Der zähe frei Fall=== | ||
| − | [[Datei:Versuchsaufbau_Wirbelstrombremse_Fallendende_Magnetkugel.jpg|thumb]] | + | [[Datei:Versuchsaufbau_Wirbelstrombremse_Fallendende_Magnetkugel.jpg|thumb|Dieser Neodym-Magnet hat die Form einer Kugel.]] |
| + | ;Aufbau | ||
| + | Man läßt einen Permanentmagneten<ref>Wenn man einen kugelförmigen Magneten hat und eine gleichgroße Stahlkugel, kann man auch ein bischen "zaubern": Man läßt zuerst die Stahlkugel durchfallen und behauptet man könne sie mit einem Zauberspruch verwandeln. Heimlich tauscht man die Stahlkugel gegen die Magnetkugel aus und läßt sie durch das Rohr fallen :) | ||
| + | <br/>Ein kleiner Scheibenmagnet hat den Vorteil, dass sich seine Flugbahn stabilisiert, beim Blick ins Rohr gut verfolgen läßt, und man für die Erklärung eine übersichtlichere Situation hat.</ref> durch ein Kupferrohr fallen. Man kann auch ein Kunststoffrohr ausprobieren. | ||
| + | |||
| + | ;Beobachtung | ||
| + | Der Magnet fällt nur ganz langsam und mit konstanter Geschwindigkeit durch das Kupferrohr. Durch das Plastikrohr fällt er "ganz normal". | ||
| + | |||
| + | ;Erklärung | ||
| + | Die Situation ähnelt sehr stark dem in der Spule schwingenden Magneten. Das Kupferrohr entspricht dabei der Spule. Bewegt sich der Magnet nach unten, so ändert sich besonders in der Nähe der Pole der magnetische Fluss durch die Querschnittsfläche des Rohrs. Dadurch entstehen zwei Kreisströme, die wiederum ein Magnetfeld erzeugen. Das entstehende Magnetfeld ist so orientiert, dass es die Bewegung des Magneten hemmt. | ||
| + | |||
| + | Wenn der Magnet mit einer konstanten Geschwindigkeit fällt, ist die Bremskraft entgegengesetzt gleich zu seiner Gewichtskraft. Offensichtlich ist die Bremskraft von der Geschwindigkeit abhängig. Je schneller der Magnet ist, desto größer ist die Bremskraft, bis schließlich ein Gleichgewicht herrscht.<ref>So ähnlich wie der Sprung eines Fallschirmspringers mit Luftreibung.</ref> | ||
| + | |||
| + | Am Anfang der Fallbewegung wird die potentielle Energie des Magneten benötigt, um den Magneten in Bewegung zu versetzen und das Magnetfeld zu erzeugen. Ausserdem ist die Energie nötig um den Strom anzutreiben, der das Rohr erwärmt. Fällt der Magnet mit einer konstanten Geschwindigkeit, so wird also das Rohr mit einer konstanten Leistung erwärmt. Dann wird die potentielle Energie des Magneten nur noch zur Erwärmung des Rohres genutzt, die Bewegungsenergie und die Energie des Magnetfeldes sind dann konstant. | ||
| + | |||
| + | ;Erklärung mit [[Kraftwirkung_auf_elektrische_Ströme_im_Magnetfeld_-_die_Lorentzkraft#Versuch:_Magnetfelduntersuchung_mit_einem_Probestrom|Probeströmen]] im Feld | ||
| + | {| | ||
| + | | | ||
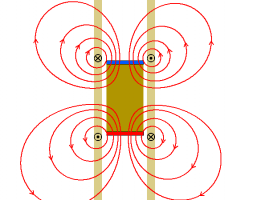
| + | [[Datei:Wirbelströme_Fallender_Magnet_im_Kupferrohr_ProbeStröme.png|thumb|260px]] | ||
| + | |valign="top"| | ||
| + | An den Stellen der stärksten Flussveränderung<ref>Ungefähr dort, wo die Feldstärke senkrecht auf der Querschnittsfläche des Rohres steht.</ref> bilden sich Kreisströme aus. Diese kann man wie Probekörper, bzw. Probeströme im Feld des Magneten betrachten. Nach der [[Kraftwirkung_auf_elektrische_Ströme_im_Magnetfeld_-_die_Lorentzkraft#Versuch:_Ein_Kabel_im_Magnetfeld_-_die_Leiterschaukel|Drei-Finger-Regel]] wird der untere Kreisstrom vom Magneten nach unten gedrückt und der obere wird nach unten gezogen. Nach dem [[Die_Kraft#Das_Wechselwirkungsprinzip_("actio = reactio")|actio-reactio-Prinzip]] wird daher der Magnet vom unteren Strom nach oben gedrückt und vom oberen nach oben gezogen. | ||
| + | |} | ||
| + | |||
| + | ;Erklärung mit dem [[Fern-_und_Nahwirkungstheorie#"aktives"_Feld_mit_Zug-_und_Druckspannungen|aktiven Feld]] | ||
| + | <gallery widths=260px heights=200px perrow=2> | ||
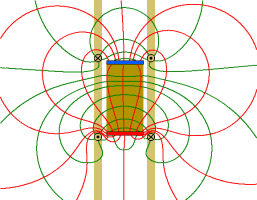
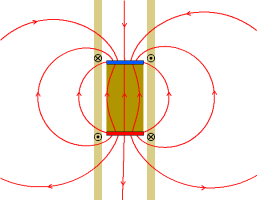
| + | Bild:Wirbelströme Fallender Magnet ohne Kupferrohr.png|Im Modell des aktiven Feldes werden Feldlinien und Flächen des Magneten... | ||
| + | Bild:Wirbelströme Fallender Magnet mit Kupferrohr.png|durch die Wirbelströme im Rohr verändert. Der Magnet wird mit Hilfe des Feldes "an den Strömen aufgehängt". (vgl. [[Graphische_Darstellung_von_Feldern#Druck-_und_Zugspannung|Zug und Druck in Feldern]].) | ||
| + | Bild:Wirbelströme_Fallender_Magnet_im_Kupferrohr_ProbeStröme.png|Das Feld ergibt sich als Überlagerung des Feldes des Permanentmagneten... | ||
| + | Bild:Wirbelströme_Fallender_Magnet_im_Kupferrohr_Ströme_Linien.png|mit dem Wirbelfeld der induzierten Kreisströme. | ||
| + | </gallery> | ||
| + | |||
| + | |||
| + | <br style="clear: both" /> | ||
| + | |||
[[Datei:Versuchsaufbau_Wirbelstrombremse_Fallendender_Ring.jpg|thumb]] | [[Datei:Versuchsaufbau_Wirbelstrombremse_Fallendender_Ring.jpg|thumb]] | ||
| − | <br style="clear: both" /> | + | <br style="clear: both" /> |
===Die gebremste Scheibe=== | ===Die gebremste Scheibe=== | ||
| Zeile 95: | Zeile 192: | ||
:<math> F=\frac{(v\, b\, B)^2}{R\,v}</math> | :<math> F=\frac{(v\, b\, B)^2}{R\,v}</math> | ||
| − | + | {|class="wikitable" | |
| − | + | |style="border-style: solid; border-width: 4px "| | |
| − | + | :<math>F=\frac{ b^2 \, B^2}{R}\,v</math> | |
| − | + | Die Bremskraft ist proportional zur Geschwindigkeit, zum Quadrat der Flussdichte und der Feldbreite und | |
| + | <br>antiproportional zum ohmschen Widerstand. | ||
| + | |} | ||
| − | + | Eine Wirbelstrombremse bremst also einen schnellen Körper stärker als einen langsamen! | |
Die Bremswirkung einer Wirbelstrombremse ist damit gänzlich verschieden von einer reibungsbasierten Bremse, wie zB. eine Scheibenbremse. Denn die Gleitreibung ist weitgehend von der Geschwindigkeit unabhängig und somit zeitlich konstant. | Die Bremswirkung einer Wirbelstrombremse ist damit gänzlich verschieden von einer reibungsbasierten Bremse, wie zB. eine Scheibenbremse. Denn die Gleitreibung ist weitgehend von der Geschwindigkeit unabhängig und somit zeitlich konstant. | ||
| Zeile 106: | Zeile 205: | ||
Verliert eine Schwingung durch eine Wirbelstrombremse Energie, so nimmt die Amplitude exponentiell ab. (Vergleiche Gedämpfte Schwingungen.) | Verliert eine Schwingung durch eine Wirbelstrombremse Energie, so nimmt die Amplitude exponentiell ab. (Vergleiche Gedämpfte Schwingungen.) | ||
| + | Wegen der Proportionalität zur Geschwindigkeit kann man die Bremskraft mit einem laminaren Strömungswiderstand vergleichen. Das ist bei kleinen Tröpfchen in Luft der Fall oder bei etwas größeren Kugeln in Wasser oder Öl. Bei größeren Gegenständen wird die Strömung turbulent und der Widerstand nimmt quadratisch mit der der Geschwindigkeit zu. | ||
| + | |||
| + | ==Supraleitung: Stromfluss ohne Energieverlust== | ||
| + | |||
| + | Bei allen Versuchen spielt der ohmsche Widerstand der Spule, des Kupferrohrs, der Alufolie,... eine wichtige Rolle. | ||
| + | Was würde passieren, wenn eine Spule keinen Widerstand mehr hätte? Das kann man sich in diesen Videos anschauen und erklären lassen: | ||
| + | *[https://www.youtube.com/watch?v=HRLvVkkq5GE Ein Magnet wird auf einen Supraleiter gesetzt] "Meissner Effect" von "Harvard Natural Sciences Lecture Demonstrations", youtube | ||
| + | *[https://www.youtube.com/watch?v=vruYFOlM1-Q Die Quantenmechanik der Supraleitung!] von "Arvin Ash", youtube | ||
| + | *[https://www.youtube.com/watch?v=bD2M7P6dTVA Erklärung der Effekte der Supraleitung] "The Map of Superconductivity" von "Domain of Science", youtube | ||
| + | *[https://www.youtube.com/watch?v=h6FYs_AUCsQ The Physics of superconductors] von "Higgsino physics", youtube | ||
==Links== | ==Links== | ||
*[http://de.wikipedia.org/wiki/Wirbelstrombremse Wikipedia: Wirbelstrombremse] | *[http://de.wikipedia.org/wiki/Wirbelstrombremse Wikipedia: Wirbelstrombremse] | ||
*[http://de.wikipedia.org/wiki/Wirbelstrom Wikipedia: Wirbelstrom] | *[http://de.wikipedia.org/wiki/Wirbelstrom Wikipedia: Wirbelstrom] | ||
| + | *[http://www.youtube.com/watch?v=k4xsqw463Hs Video]: Es wird ein Eisenstück per Induktion zum Glühen gebracht. (youtube: "Induction Forge - Show and tell" von "Mark Aspery") | ||
| + | *Video: [https://www.youtube.com/watch?v=sENgdSF8ppA Copper's Surprising Reaction to Strong Magnets | Force Field Motion Dampening] youtube "NightHawkInLight" | ||
| + | |||
| + | ==Fußnoten== | ||
| + | <references /> | ||
Aktuelle Version vom 19. Oktober 2022, 08:22 Uhr
(Kursstufe > Elektro-Magnetismus)
Die Wirkung der Induktion ist so gerichtet, dass sie der Ursache der Induktion entgegenwirkt. ("Lenzsche Regel")
- Wenn der magnetische Fluss durch eine Spule zunimmt (abnimmt), so fließt der induzierte Strom so durch die Spule, dass das dadurch entstandene Magnetfeld entgegengerichtet (gleichgerichtet) ist und somit versucht den magnetischen Fluss aufrecht zu erhalten.
- Wenn der Stromfluss durch eine Spule sich vergrößert (verkleinert), so wird eine Spannung induziert, die den Stromfluss hemmt (verstärkt) und somit versucht die Stromstärke aufrecht zu erhalten.
- Wenn durch eine Bewegung eines Magneten sich in einem leitenden Material der magnetische Fluss ändert, so wird durch den induzierten Strom ein Magnetfeld erzeugt, dass die Bewegung des Magneten bremst.
Die Lenzsche Regel ist ein Spezialfall der Energieerhaltung. Das erkennt man, wenn man annimmt, die Wirkung der Induktion wäre anders gerichtet.
- Durch die Zunahme des magnetischen Flusses würde der Fluss noch größer und somit beliebig groß.
- Durch eine Zunahme der Stromstärke würde die Stromstärke weiter ansteigen und beliebig groß werden.
- Durch eine Zunahme der Geschwindigkeit würde sie noch größer und beliebig groß.
In allen Fällen hätte man ein Perpetuum mobile, das ständig aus dem Nichts Energie erzeugen würde.
Um der Lenzschen Regel im Induktionsgesetz Rechnung zu tragen, setzt man ein Minuszeichen vor die Induktionsspannung:
- [math]U=-\dot\Phi[/math]
Erklärung mit der Lorentzkraft:
- Bewegung im Feld bewirkt einen Strom
- Dieser Strom fließt in einem Feld und es wirkt wiederum eine Kraft
Inhaltsverzeichnis
- 1 Versuche
- 1.1 Schwingender Magnet
- 1.2 Der Fahrraddynamo
- 1.3 Der Kurbel-Generator (Dynamot)
- 1.4 Der belastete Transformator
- 1.5 Die Induktionskochplatte
- 1.6 Der Katapultring
- 1.7 Die Ringschaukel
- 1.8 Das Waltenhofsche Pendel
- 1.9 Das angetriebene und gebremste Teelicht
- 1.10 Der zähe frei Fall
- 1.11 Die gebremste Scheibe
- 2 Berechnung der Bremskraft einer Wirbelstrombremse
- 3 Supraleitung: Stromfluss ohne Energieverlust
- 4 Links
- 5 Fußnoten
Versuche
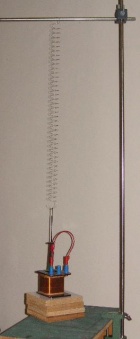
Schwingender Magnet
- Aufbau
Aus einem Stabmagnet und einer Feder baut man ein Federpendel. Eine Spule mit ca. 500 Windungen wird so platziert, dass ein Pol des Magneten innerhalb der Spule schwingt.
- Man schubst zunächst das Federpendel an und
- verbindet nach einigen Sekunden Anfang und Ende der Spule mit einem Kabel.
- Beobachtung
- Der Magnet schwingt zunächst mit einer relativ konstanten Amplitude,
- nach dem Anbringen des Kabels nimmt die Amplitude relativ schnell ab und der Magnet kommt zum Stehen.
- Folgerung
|
Offensichtlich kann die geschlossene Spule der Schwingung Energie entziehen, was bei geöffneter Spule nicht gelingt.
|
Am blauen Punkt kann man den Magneten bewegen.
|
Der Fahrraddynamo
- Aufbau
Man benötigt ein Fahrrad mit einem Nabendynamo am Vorderrad. Man hebt das Vorderrad des Fahrrades an und schubst den Vorderreifen an. Dann wartet man ab.
Das macht man einmal mit ausgeschaltetem Licht. Dann schaltet man während sich das Rad dreht, das Licht an.
- Beobachtung
Schaltet man das Licht ein, wird das Rad merklich langsamer und bleibt schneller stehen.
- Erklärung
Durch das Anschubsen wird Energie in die Drehbewegung des Rades übertragen. Bei ausgeschaltetem Licht geht die Bewegungsenergie durch die Reibung im Lager und an der Luft aus dem Rad, wodurch das Lager und die Luft leicht erwärmt werden. (Das müßte man nachmessen, ist aber nicht leicht.)
Schaltet man das Licht ein, wird für den Betrieb der Lampe viel Energie benötigt, die aus dem drehenden Rad kommt. Das Rad wird daher schneller abgebremst.
Der Kurbel-Generator (Dynamot)
- Aufbau
Man dreht den Dynamo, um die Lampe (6V/30W) zum Leuchten zu bringen und jemand schaltet die Lampe an und aus. (Schließt und öffnet den Stromkreis.)
- Beobachtung
Schaltet man die Lampe an, ist es richtig anstrengend die Dynamokurbel zu drehen, schaltet man die Lampe aus, geht es viel leichter.
- Erklärung
Durch das Kurbeln treibt man den Vorgang an und liefert die dazu nötige Energie. Wird die Lampe angeschaltet, so muß man viel Energie lieren, um sie zu betreiben. Ist die Lampe ausgeschaltet, braucht man nur ein bisschen Energie, um die Reibung innerhalb des Dynamos zu überwinden. Genauso ergeht es auch den Kraftwerken in unserem Stromnetz: werden zur Mittagszeit viele elektrische Geräte eingeschaltet, müssen sie mehr Energie liefern als Nachts, wenn viele Geräte ausgeschaltet sind!
Der belastete Transformator
vergrößern
Die Induktionskochplatte
- Aufbau
Auf eine Induktonskochplatte wird eine Stück Alufolie gelegt und die Platte eingeschaltet.
Die Kochplatte ist mit Hilfe von 4 Spulen nachgebaut worden. Die Spulen haben 500 Windungen, je 2 sind parallel und diese wieder in Reihe geschaltet und mit der Netzspannung verbunden. An jeder Spule liegt also die halbe Netzspannung an. (Schaltet man alle Spulen parallel, so ist der Effekt zwar größer, aber die Sicherung springt ständig raus :) Die 4 Eisenstangen dienen nur der Stabilisierung der Platte.
Auf die Eisenkerne wird eine Aluplatte gelegt und der Strom eingeschaltet.
- Beobachtung
 Hier das Video des Versuchs |
 Hier das Video des Versuchs |
In diesem Video wird ein Eisenstück per Induktion zum Glühen gebracht. (youtube: "Induction Forge - Show and tell" von "Mark Aspery")
- Erklärung
Der Katapultring
Die Ringschaukel
- Mit Permanentmagnet
- Mit Elektromagnet
Das Waltenhofsche Pendel
Mit und ohne Schlitz im Ring
Rechteck und Kamm
Wie fließt der Strom?
Das angetriebene und gebremste Teelicht
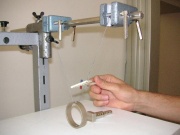
Der zähe frei Fall
- Aufbau
Man läßt einen Permanentmagneten[1] durch ein Kupferrohr fallen. Man kann auch ein Kunststoffrohr ausprobieren.
- Beobachtung
Der Magnet fällt nur ganz langsam und mit konstanter Geschwindigkeit durch das Kupferrohr. Durch das Plastikrohr fällt er "ganz normal".
- Erklärung
Die Situation ähnelt sehr stark dem in der Spule schwingenden Magneten. Das Kupferrohr entspricht dabei der Spule. Bewegt sich der Magnet nach unten, so ändert sich besonders in der Nähe der Pole der magnetische Fluss durch die Querschnittsfläche des Rohrs. Dadurch entstehen zwei Kreisströme, die wiederum ein Magnetfeld erzeugen. Das entstehende Magnetfeld ist so orientiert, dass es die Bewegung des Magneten hemmt.
Wenn der Magnet mit einer konstanten Geschwindigkeit fällt, ist die Bremskraft entgegengesetzt gleich zu seiner Gewichtskraft. Offensichtlich ist die Bremskraft von der Geschwindigkeit abhängig. Je schneller der Magnet ist, desto größer ist die Bremskraft, bis schließlich ein Gleichgewicht herrscht.[2]
Am Anfang der Fallbewegung wird die potentielle Energie des Magneten benötigt, um den Magneten in Bewegung zu versetzen und das Magnetfeld zu erzeugen. Ausserdem ist die Energie nötig um den Strom anzutreiben, der das Rohr erwärmt. Fällt der Magnet mit einer konstanten Geschwindigkeit, so wird also das Rohr mit einer konstanten Leistung erwärmt. Dann wird die potentielle Energie des Magneten nur noch zur Erwärmung des Rohres genutzt, die Bewegungsenergie und die Energie des Magnetfeldes sind dann konstant.
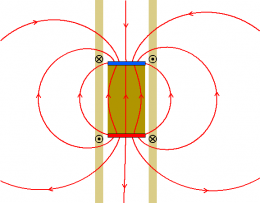
- Erklärung mit Probeströmen im Feld
|
An den Stellen der stärksten Flussveränderung[3] bilden sich Kreisströme aus. Diese kann man wie Probekörper, bzw. Probeströme im Feld des Magneten betrachten. Nach der Drei-Finger-Regel wird der untere Kreisstrom vom Magneten nach unten gedrückt und der obere wird nach unten gezogen. Nach dem actio-reactio-Prinzip wird daher der Magnet vom unteren Strom nach oben gedrückt und vom oberen nach oben gezogen. |
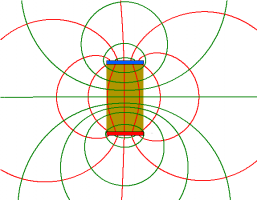
- Erklärung mit dem aktiven Feld
durch die Wirbelströme im Rohr verändert. Der Magnet wird mit Hilfe des Feldes "an den Strömen aufgehängt". (vgl. Zug und Druck in Feldern.)
Die gebremste Scheibe
Berechnung der Bremskraft einer Wirbelstrombremse
Um eine Berechnung durchzuführen, muss man die Situation vereinfachen. Wir nehmen an, dass ein leitender Gegenstand mit der Geschwindigkeit v in ein Magnetfeld der Breite b und der Flussdichte B eintaucht. Die Feldlinien stehen senkrecht auf der Oberfläche.
Die Spannung, die den Strom antreibt, beträgt:
- [math]U = \dot \Phi = \dot A \, B = v\, b \, B[/math]
In dem leitenden Gegenstand erfährt der Strom den Widerstand R, für die Stromstärke folgt also nach dem ohmschen Gesetz:
- [math] I = \frac{U}{R} = \frac{v\, b \, B}{R}[/math]
Nach dem Energieerhaltungssatz fließt genausoviel Energie herein wie heraus. Für die Bewegung in das Magnetfeld hinein bedarf es einer mechanischen Energie, die den Strom antreibt. Man kann also die Energiestromstärke (Leistung) auf zwei Arten berechnen, mechanisch und elektrisch:
- [math]P_{mech}=P_{el}[/math]
- [math]\frac{F\, s}{t}= F\, v=U\, I[/math]
- [math]F = \frac{U\, I}{v}[/math]
Jetzt kann man die Ergebnisse von oben einsetzen:
- [math] F=\frac{(v\, b\, B)^2}{R\,v}[/math]
Die Bremskraft ist proportional zur Geschwindigkeit, zum Quadrat der Flussdichte und der Feldbreite und
|
Eine Wirbelstrombremse bremst also einen schnellen Körper stärker als einen langsamen!
Die Bremswirkung einer Wirbelstrombremse ist damit gänzlich verschieden von einer reibungsbasierten Bremse, wie zB. eine Scheibenbremse. Denn die Gleitreibung ist weitgehend von der Geschwindigkeit unabhängig und somit zeitlich konstant.
Verliert eine Schwingung durch eine Wirbelstrombremse Energie, so nimmt die Amplitude exponentiell ab. (Vergleiche Gedämpfte Schwingungen.)
Wegen der Proportionalität zur Geschwindigkeit kann man die Bremskraft mit einem laminaren Strömungswiderstand vergleichen. Das ist bei kleinen Tröpfchen in Luft der Fall oder bei etwas größeren Kugeln in Wasser oder Öl. Bei größeren Gegenständen wird die Strömung turbulent und der Widerstand nimmt quadratisch mit der der Geschwindigkeit zu.
Supraleitung: Stromfluss ohne Energieverlust
Bei allen Versuchen spielt der ohmsche Widerstand der Spule, des Kupferrohrs, der Alufolie,... eine wichtige Rolle. Was würde passieren, wenn eine Spule keinen Widerstand mehr hätte? Das kann man sich in diesen Videos anschauen und erklären lassen:
- Ein Magnet wird auf einen Supraleiter gesetzt "Meissner Effect" von "Harvard Natural Sciences Lecture Demonstrations", youtube
- Die Quantenmechanik der Supraleitung! von "Arvin Ash", youtube
- Erklärung der Effekte der Supraleitung "The Map of Superconductivity" von "Domain of Science", youtube
- The Physics of superconductors von "Higgsino physics", youtube
Links
- Wikipedia: Wirbelstrombremse
- Wikipedia: Wirbelstrom
- Video: Es wird ein Eisenstück per Induktion zum Glühen gebracht. (youtube: "Induction Forge - Show and tell" von "Mark Aspery")
- Video: Copper's Surprising Reaction to Strong Magnets | Force Field Motion Dampening youtube "NightHawkInLight"
Fußnoten
- ↑ Wenn man einen kugelförmigen Magneten hat und eine gleichgroße Stahlkugel, kann man auch ein bischen "zaubern": Man läßt zuerst die Stahlkugel durchfallen und behauptet man könne sie mit einem Zauberspruch verwandeln. Heimlich tauscht man die Stahlkugel gegen die Magnetkugel aus und läßt sie durch das Rohr fallen :)
Ein kleiner Scheibenmagnet hat den Vorteil, dass sich seine Flugbahn stabilisiert, beim Blick ins Rohr gut verfolgen läßt, und man für die Erklärung eine übersichtlichere Situation hat. - ↑ So ähnlich wie der Sprung eines Fallschirmspringers mit Luftreibung.
- ↑ Ungefähr dort, wo die Feldstärke senkrecht auf der Querschnittsfläche des Rohres steht.