Zerlegung in harmonische Schwingungen (Fourieranalyse): Unterschied zwischen den Versionen

Aus Schulphysikwiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „ ==Versuch: Frequenzanalyse mit dem Computer== ===Aufbau:=== Ein Mikrophon wird an einen Computer angeschlossen. (CASSY) Die Software analysiert die aufgenommene …“)
 
(→‎Links)
 
(7 dazwischenliegende Versionen des gleichen Benutzers werden nicht angezeigt)
Zeile 1: Zeile 1:
 +
([[Inhalt_Kursstufe|'''Kursstufe''']] > [[Inhalt_Kursstufe#Mechanische Schwingungen|''' Mechanische Schwingungen''']])
 +
 +
 +
<gallery widths=150px heights=130px  perrow=4>
 +
Bild:Ohr.jpg|Wie können wir mit unserem Ohr zwei oder mehrere Töne gleichzeitig hören?
 +
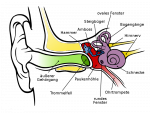
Bild:Ohr_schematisch.svg.png|Video: [https://www.planet-schule.de/sf/filme-online.php?film=6906 "Superohren" Hohe Töne, tiefe Töne (ab 6:46)]
 +
Bild:Saxophon_Candy_Dulfer.jpg|Warum klingt ein "a" eines Saxophons anders als ein gesungenes "a" oder das einer Flöte?
 +
Bild:Gitarre_Django_Reinhardt.jpg|Warum hängt der Klang davon ab, ob man mit dem Plektrum oder dem Finger zupft?
 +
</gallery>
  
 
==Versuch: Frequenzanalyse mit dem Computer==
 
==Versuch: Frequenzanalyse mit dem Computer==
Zeile 53: Zeile 62:
  
 
==Links==
 
==Links==
−
*[[Media:Überlagerung zweier harmonischer Schwingungen Applet.zip|Applet zur Überlagerung zweier harmonischer Wellen (ca. 1MB)]]
+
*Video: [https://www.planet-schule.de/sf/filme-online.php?film=6906 "Superohren" Hohe Töne, tiefe Töne (ab 6:46)] SWR: Planet Schule "Superohren"
−
*[http://www.schulphysik.de/ntnujava/sound/sound.html Applet Fouriersynthese]
+
*Video: [https://www.youtube.com/watch?v=spUNpyF58BY Was ist eine Fourier-Transformation? Eine visuelle Einführung] (in english, deutsche Untertitel) "3Blue1Brown", youtube
 +
*[https://phet.colorado.edu/sims/html/fourier-making-waves/latest/fourier-making-waves_de.html Applet Fouriersynthese] PhET Interactive Simulations, University of Colorado Boulder
 +
*Wikipedia: [https://de.wikipedia.org/wiki/Saitenschwingung Saitenschwingung]
 +
*Hausarbeit: [https://www.math.uni-hamburg.de/home/muelich/ss08/vortraege/SchwingendeSaite2008ShtZ_0407.pdf Die schwingende Saite, periodische Lösungen der Wellengleichung] Stephan h.t. Zahrte, Proseminar Fourier-Analysis, Uni Hamburg im Sommersemester 2008
 +
*Software zur Frequenzanalyse
 +
**[http://www.zeitnitz.eu/scms/scope_de?mid=3.01 PC-Oszilloskop "Scope"] (Christian Zeitnitz, kostenlos für Privatanwender und Schulen)
 +
**[http://www.zen22142.zen.co.uk/Prac/winscope.htm PC-Oszilloskop "Winscope"] (Andy Collinson, kostenlos)
 +
**[https://gitorious.org/osqoop/pages/Home#toc_0 PC-Oszilloskop "Osqoop"] (Nicht so einfach zu installieren ([http://nonlinear.eecs.berkeley.edu/chaos/Osqoop_Build_Instructions.txt Tipps]), benötigt QT4)

Aktuelle Version vom 8. Dezember 2021, 07:53 Uhr

(Kursstufe > Mechanische Schwingungen)


  • Wie können wir mit unserem Ohr zwei oder mehrere Töne gleichzeitig hören?

  • Warum klingt ein "a" eines Saxophons anders als ein gesungenes "a" oder das einer Flöte?

  • Warum hängt der Klang davon ab, ob man mit dem Plektrum oder dem Finger zupft?

Versuch: Frequenzanalyse mit dem Computer

Aufbau:

Ein Mikrophon wird an einen Computer angeschlossen. (CASSY) Die Software analysiert die aufgenommene (nichtharmonische!) Schwingung, indem sie harmonische Schwingungen sucht, zu denen man die aufgenommene Schwingen überlagern kann. Das Programm muss also zu jeder Frequenz eine Amplitude suchen.

Angezeigt wird die Amplitude über der Frequenz, das sogenannte Frequenzspektrum oder auch Spektrum.

Wir singen verschiedene Töne und spielen Musikinstrumente.


Beobachtung:

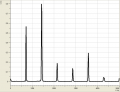
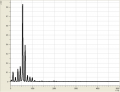
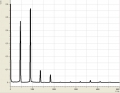
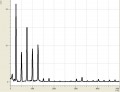
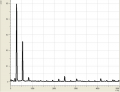
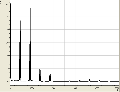
Allgemein haben wir bei den verschiedenen Tönen beobachten können, dass sie sowohl aus wenigen (bis zu einem), als auch aus vielen (bei uns waren es bis zu 6) Obertönen bestehen können. So bestand z.B. ein mit dem Mund erzeugtes "a" aus etwa 5 Obertönen, die sich in dem Bereich um 2000Hz verteilten. Hingegen kennzeichnete sich ein "a", welches mit dem Fagott gespielt wurde durch eigentlich nur einen Oberton bei 1000Hz aus. Senken wir jedoch die Frequenz, erkennen wir ein häufigeres Auftreten von Obertönen.

Spektren eines Fagotts
  • Spektren eines Fagotts

  • Mundstück

  • a

  • gestrichenes a

  • tiefes a

  • gestrichenes h

  • tiefes b

Spektren gesungener Vokale
  • Gesungene Vokale

  • A

  • E

  • I

  • O

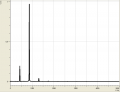
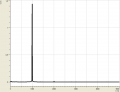
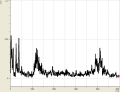
Stimmgabel und Rauschen

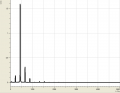
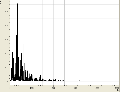
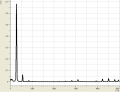
Weiterhin sind wir noch auf zwei extreme Spezialfälle gestoßen: Einmal betrachteten wir eine Stimmgabel, welche sehr wenig Obertöne besaß. Der Amplitude des großen Obertons wurde eine Frequenz von ziemlich genau 1000Hz zugeordnet. Anderseits betrachteten wir "Rauschen", welches sich, wie wir sahen, durch viele Obertöne, also durch relativ hohe Amplituden bei möglichst jeder Frequenz, kennzeichnet.

  • 1000Hz-Stimmgabel

  • Frequenzspektrum eines mit dem Mund erzeugten Rauschens.


Erklärung

Das Frequenzspektrum hat uns also Auskunft über die harmonischen Schwingungen der verschiedenen Töne gegeben und gezeigt dass ein Ton, den wir als einen Ton wahr nehmen nicht immer nur aus einer Schwingung besteht. Bei der Stimmgabel sehen wir jedoch genau eine Schwingung (die anderen analysierten Töne seien vernachlässigt, entstehung vielleicht durch Geräusche im Raum). Das ist hierbei aber ziemlich unbeeindruckend, da sie dafür gebaut ist Musikinstrumente zu stimmen und genau auf 1000Hz geeicht ist. Das Gegenextrem zu einem Oberton ist, wie schon in der Beobachtung gesehen, das Rauschen. Auch hier gibt es eine Besonderheit, und zwar wenn jeder Frequenz die gleiche Amplitude zugeordnet wird nennt man das: Weisses Rauschen.

Links

Von „http://schulphysikwiki.de/index.php?title=Zerlegung_in_harmonische_Schwingungen_(Fourieranalyse)&oldid=16137“