|
|
| (55 dazwischenliegende Versionen des gleichen Benutzers werden nicht angezeigt) |
| Zeile 1: |
Zeile 1: |
| | + | ([[Inhalt_Klasse_10|'''Klassische Mechanik''']] > [[Inhalt_Klasse_10#Trägheit_und_Impuls|'''Trägheit und Impuls''']]) |
| | + | |
| | ==Beispiele== | | ==Beispiele== |
| | + | <gallery widths=150px heights=130px perrow=4 > |
| | + | Bild:Luftgewehr Kugel.jpg|Eine Luftgewehrkugel |
| | + | Bild:Holzbrett Luftgewehr.jpg|kann dieses Brettchen umstoßen! |
| | + | Bild:Golfball.jpg|Diese Bälle... |
| | + | Bild:Tennisball.jpg|...können das auch. |
| | + | Bild:Curling_Abstoß.jpg|<ref>[http://commons.wikimedia.org/wiki/File:Martin_Sesaker_at_the_2012_Youth_Winter_Olympics.jpg Bild von Ralf Roletschek, CC by SA 3.0]</ref>Beim Curling muss man dem Stein den richtigen Schwung mitgeben, |
| | + | Bild:Curling_Besen.jpg|damit er genau am Ziel stehenbleibt. |
| | + | Bild:Luftkissenpuck.jpg|Wie funktioniert dieser "Fußball"? |
| | + | Bild:Einkaufswagen_voll.png| Wie bewegt sich ein "angeschubster" Einkaufswagen? |
| | + | </gallery> |
| | + | |
| | + | *Verschiedene Bälle, am besten gleich groß aber mit unterschiedlichen Massen, fangen und werfen. (Oder "Kegeln", denn dabei spielt die Gewichtskraft keine Rolle. Oder "Dosenwerfen" mit verschiedenen Bällen.) |
| | + | *Ein sich schnell drehendes Fahrrad-Rad kann man nicht so ohne weiteres anschubsen, abbremsen oder kippen. Es "wehrt sich". |
| | * Beispiel mit reibungsarmen Einkaufswagen: Der Wagen bewegt sich geradlinig und behält seine Geschwindigkeit bei. Auch die Drehung des Wagen ändert sich nicht. | | * Beispiel mit reibungsarmen Einkaufswagen: Der Wagen bewegt sich geradlinig und behält seine Geschwindigkeit bei. Auch die Drehung des Wagen ändert sich nicht. |
| − | *Ein sich schnell drehendes Fahrrad-Rad kann man nicht so ohne weiteres kippen. Es "wehrt sich".
| |
| | | | |
| − | Weitere Beispiele sind der Luftkissenpuck (Fußball), ein Mensch auf einem Bürodrehstuhl oder Experimente am Luftkissentisch oder -bahn. | + | Weitere Beispiele sind der Luftkissenpuck (Fußball), ein Mensch auf einem Bürodrehstuhl oder Experimente am Luftkissentisch oder -bahn. |
| | | | |
| − | ===(Dreh-)Impuls als Bewegungszustand===
| + | ==(Dreh-)Impuls als Bewegungsmenge== |
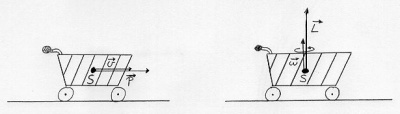
| − | [[Image:Mechanik_Bewegungszustand.jpg|thumb|400px|Der Bewegungszustand eines Einkaufswagens.]] | + | ====Definition des (Dreh-) Impulses==== |
| − | *Den Bewegungszustand eines Körpers kann man als eine Überlagerung einer Translation im Raum und eine Drehung in sich beschreiben. | + | [[Image:Mechanik_Bewegungszustand.jpg|thumb|400px|Die Bewegungsmenge eines Einkaufswagens.]] |
| | + | * Ein Ball enthält viel "Bewegung", wenn er eine große Masse hat und er schnell ist. Die physikalische Größe, welche die Bewegungsmenge angibt, heißt "Impuls". Man legt den Impuls daher als Produkt von Masse und Geschwindigkeit fest. |
| | + | :Leider hat die Einheit des Impulses keinen allgemeingültigen eigenen Namen bekommen, im Karlsruher Physikkurs wird sie nach [https://de.wikipedia.org/wiki/Christiaan_Huygens Christiaan Huygens] (1629–1695) benannt. |
| | + | *Umgangssprachlich versteht man unter "Impuls" etwas anderes als in der Physik! |
| | + | **Eine Anregung, ein Anreiz, ein Ansporn: "Der Telefonanruf ihrer Freundin war der entscheidende Impuls doch noch für die Arbeit zu lernen." ; "Der Comic ist ein guter Impuls für eine Diskussion." |
| | + | **Etwas plötzliches, kurzzeitiges: "Manchmal handelt er sehr impulsiv ohne nachzudenken." |
| | + | :{|class="wikitable" |
| | + | |style="border-style: solid; border-width: 4px "| |
| | + | Impuls- und Geschwindigkeitsvektor sind parallel, |
| | + | <br>die Masse ist der Proportionalitätsfaktor: |
| | | | |
| − | *Der Bewegungszustand wird durch die Menge an Impuls <math>\vec p</math>(Schwung) für die Translation und Drehimpuls <math>\vec L</math> (Drehschwung) für die Rotation angegeben.
| + | :<math>\vec p = m \vec v</math> |
| | + | :<math>[\vec p\,] = \mathrm{1kg \frac{1m}{1s} = 1Hy}</math> (lies: Huygens) |
| | + | |} |
| | | | |
| − | *Sowohl Impuls als auch Drehimpuls haben eine Richtung und sind vektorielle Größen. Sie geben an, wieviel Schwung, bzw. Drehschwung ein Gegenstand hat, also wieviel "Bewegungsmenge" in dem Körper steckt. Ausserdem gibt er an in welche Richtung er sich bewegt, bzw. um welche Achse er sich dreht. | + | * Ein Rad enthält viel Drehimpuls, wenn es schnell rotiert und eine große Masse möglichst weit entfernt von der Drehachse hat. |
| | + | :Die Trägheit gegenüber Drehungen, sozusagen die "Drehmasse", gibt das Trägheitsmoment des Gegenstandes an. |
| | + | :[http://www.univie.ac.at/elearnphysik/video/PhysikI/rollendeZy_648x480.flv Video] von herabrollender Dose und Zylinder. |
| | + | :[http://www.youtube.com/watch?v=4OD4aDlAiZI Video] der Drehschwingung eines Menschen auf einem Drehstuhl. |
| | | | |
| − | *In der Schulphysik wird die Rotation von Gegenständen in der Regel vernachlässigt, man betrachtet nur die Translation.
| + | :{|class="wikitable" |
| − | | + | |style="border-style: solid; border-width: 4px "| |
| − | | + | Drehimpulsvektor und Winkelgeschwindigkeit sind ebenfalls parallel, |
| − | ===Trägheitsgesetz (1. Newtonsches Axiom===
| + | <br>Proportionalitätsfaktor ist das Trägheitsmoment<ref>Das gilt eigentlich nur für Achsen, bezüglich der Körper keine Unwucht hat, der sogenannten "Hauptträgheitsachsen". Für Drehachsen, die auch eine Symmetrieachse des Körpers sind, hat der Körper keine Unwucht. |
| − | Jeder Gegenstand behält ohne Krafteinwirkung seinen Impuls <math>\vec p</math> und Drehimpuls <math>\vec L</math> in Menge und Richtung.
| + | |
| − | | + | |
| − | ===Veränderungsgesetz (2. Newtonsches Axiom)=== | + | |
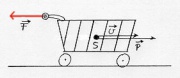
| − | [[Image:Mechanik_Änderung_Bewegungszustand.jpg|thumb|Eine Veränderung des Bewegungszustandes durch eine Kraft. Der Wagen wird langsamer.]]
| + | |
| − | Drückt oder zieht man mit einer Kraft <math>\vec F</math> an einem Gegenstand,
| + | |
| − | so wird die Richtung oder die Menge des Impulses <math>\vec p</math> verändert.
| + | |
| | | | |
| − | Dreht man mit einem Drehmoment <math>\vec M</math> ("Drehkraft") an einem Gegenstand,
| + | Ist im Abstand r von der Achse die Masse m verteilt, so beträgt das Trägheitsmoment <math>\Theta = m\ r^2</math>. |
| − | so wird die Richtung oder die Menge des Drehimpulses <math>\vec L</math> verändert.
| + | </ref>: |
| | | | |
| | + | :<math>\vec L = \Theta \, \vec \omega</math> |
| | + | |} |
| | | | |
| − | ==Berechnung des (Dreh-)Impulses und die (Winkel-)Geschwindigkeit== | + | ====Das Wasserbehältermodell==== |
| − | [[Image:Mechanik_Bewegungszustand.jpg|thumb|400px|Der Bewegungszustand eines Einkaufswagens.]]
| + | Mit Hilfe der Regler kann man die Masse und die Geschwindigkeit des Autos verändern. (Die Massen- und Geschwindigkeitsangaben sind in kg und in m/s und deshalb etwas ;) unrealistisch.) |
| | | | |
| − | *Verschiedene Bälle, am besten gleich groß aber mit unterschiedlichen Massen, fangen und werfen. | + | *Mit welcher Masse und welcher Geschwindigkeit enthält das Auto einen Impuls von 10 Hy? |
| − | *Ein Fahrradrad anschubsen, abbremsen oder kippen.
| + | |
| | | | |
| − | * Der Ball enthält viel Impuls, wenn er schnell ist und eine große Masse hat. Man legt den Impuls daher als Produkt der beiden Größen fest. Damit sind der Impuls- und Geschwindigkeitsvektor zueinander parallel und die Masse ist der Proportionalitätsfaktor:
| + | {{#widget:Iframe |
| − | :<math>\vec p = m \vec v</math>
| + | |url=https://www.geogebra.org/material/iframe/id/jGJRWYCw/width/1325/height/666/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/true/rc/false/ld/false/sdz/false/ctl/false |
| − | :Leider hat die Einheit des Impulses keinen allgemeingültigen eigenen Namen bekommen, im Karlsruher Physikkurs wird sie als "Huygens" bezeichnet. | + | |width=1000 |
| − | :<math>[\vec p] = \mathrm{1kg \frac{1m}{1s} = 1Hy}</math> (lies: Huygens)
| + | |height=500 |
| | + | |border=0 |
| | + | }} |
| | | | |
| | + | ====Bewegung als Translation und Rotation==== |
| | + | *Die Bewegung eines Körpers kann man als eine Überlagerung einer Translation im Raum und eine Drehung in sich beschreiben. |
| | | | |
| − | * Der Drehimpulsvektor und die Winkelgeschwindigkeit sind ebenfalls parallel und der Proportionalitätsfaktor ist das Trägheitsmoment des Körpers: | + | *Die Bewegung wird durch die Menge an Impuls <math>\vec p</math> (Schwung) für die Translation und Drehimpuls <math>\vec L</math> (Drehschwung) für die Rotation angegeben. |
| | | | |
| − | :<math>\vec L = \Theta \vec \omega</math>
| + | *Sowohl Impuls als auch Drehimpuls haben eine Richtung und sind vektorielle Größen. Sie geben an, wieviel Schwung, bzw. Drehschwung ein Gegenstand hat, also wieviel "Bewegungsmenge" in dem Körper steckt. Außerdem gibt er an in welche Richtung er sich bewegt, bzw. um welche Achse er sich dreht. |
| | | | |
| − | :Deshalb kann man den Bewegungszustand auch über die Geschwindigkeit und die Winkelgeschwindigkeit festlegen.
| + | *In der Schulphysik betrachtet man in der Regel Bewegungen von Gegenständen, bei denen die Drehbewegung keine Rolle spielt und beschreibt nur die Translation. |
| | | | |
| | + | ==Trägheitsgesetz (1. Newtonsches Axiom)== |
| | + | Mit Hilfe des Impulses kann man das Trägheitsgesetz genauer fassen: |
| | + | {|class="wikitable" |
| | + | |style="border-style: solid; border-width: 4px "| |
| | + | Jeder Gegenstand behält ohne Wechselwirkung mit einem anderen Körper |
| | + | <br> seinen Impuls <math>\vec p</math> und Drehimpuls <math>\vec L</math> in Menge und Richtung. |
| | + | |} |
| | | | |
| | + | ==Veränderungsgesetz (2. Newtonsches Axiom)== |
| | + | [[Image:Mechanik_Änderung_Bewegungszustand.jpg|thumb|Eine Veränderung der Bewegungsmenge durch eine Kraft. Der Impuls des Wagens nimmt ab.]] |
| | | | |
| | + | {|class="wikitable" |
| | + | |style="border-style: solid; border-width: 4px "| |
| | + | Drückt (zieht) man mit einer [[Die Kraft|Kraft]] <math>\vec F</math> an einem Gegenstand, |
| | + | <br> so wird die Richtung oder die Menge des Impulses <math>\vec p</math> verändert. |
| | + | |
| | + | Dreht man mit einem Drehmoment <math>\vec M</math> ("Drehkraft") an einem Gegenstand, |
| | + | <br> so wird die Richtung oder die Menge des Drehimpulses <math>\vec L</math> verändert. |
| | + | |} |
| | | | |
| | + | ==Aufgaben== |
| | + | ;1) Berechne jeweils die Impulsmenge |
| | + | :a) Ein Vogel mit der Masse 100 g fliegt mit 36 km/h. |
| | + | :b) Ein Fußgänger (m=72 kg) läuft mit 5 km/h. |
| | + | :c) Ein Auto (m=1 t) fährt mit 36 km/h. |
| | | | |
| − | ===Das Wasserbehältermodell===
| + | ;2) Anke und ihr Papa fahren zusammen Rad. |
| | + | :Anke wiegt 40 kg, ihr Vater 90 kg, jedes ihrer Räder 10kg. Sie fahren mit 18 km/h nebeneinander. |
| | + | :a) Wieviel Impuls steckt in Anna, in ihrem Vater und wieviel in den beiden Rädern? |
| | + | :Stelle dies mit dem Wasserbehältermodell dar. |
| | + | :b) Wie schnell muss Anke fahren, um genausoviel Impuls wie ihr Vater zu haben? (mit Rädern) |
| | + | :Stelle auch dies im Wasserbehältermodell dar. |
| | | | |
| − | Mit Hilfe der Regler kann man die Masse und die Geschwindigkeit des Autos verändern. (Die Massen- und Geschwindigkeitsangaben sind in kg und in m/s und deshalb etwas ;) unrealistisch.)
| + | ;3) Ball und Gewehrkugel |
| | + | :Ein Tennisball (m=57g) kann bei einer Geschwindigkeit von 5 km/h einen Holzklotz umschmeißen. |
| | + | :Wie schnell muß dazu eine Luftgewehrkugel sein, wenn sie nur 0,541 g Masse hat? |
| | | | |
| − | *Mit welcher Masse und welcher Geschwindigkeit enthält das Auto einen Impuls von 10 Hy?
| + | ===[[Aufgaben zum Impuls als Bewegungsmenge - Lösungen|Lösungen]]=== |
| − | | + | |
| − | <ggb_applet width="1000" height="500" version="4.2" ggbBase64="UEsDBBQACAAIAAq8VUMAAAAAAAAAAAAAAAAuAAAAN2FmNTE1MTg5MTNiZDY4MTdkNDM2MzU4NDA4ZGQwYjVcQXV0b19ibGF1LmpwZ+y7Z1BUXbQoeBARAZUPBEVAmpyD5EyDSM45g+QkIDnTKhIkShYQUHJGchSQnJGcc05Nhm46TX+37szUTL169WZ+zHs1dXfXOtW79zpr75XX6joHM49ZB/5RlleSB3DuAQAO9gNglgBZ4OGDB/gP8B7i4+MTEDwkfET2+BER0aMXpE+JyV5SgmheUlJT0zJys9DSczJQU7MKs3G+4hUQEACxiEqK8Elw8wvw/UsEh4CA4BHRI4rHjyn46Kjp+P4fD0wnQPIQJxa3HReHHrhHgoNLgoPpAUDYc+Lh/McA/nPg3MO9j/cA/yEBIREWof4f4B4OLu69+7h4ePfvY1eDsevAfRI8UjpemQdPtSzx6d3J+D4m/HzI8Lr6D7n2xBkjv5XHJwLCZ88pXlAyMbOwsrELCAoJi4iKyb6Rk1dQVFLW0dXTNzA0Mra2sbWzd3B08vTy9vH18w8I/RwWHhH5JSoxKTklNe1bekZuXn5BYVFxSWlNbV19Q2NTc0tXd09vX//A4NDk1PTM7Nz8wuLG5tb2zu7e/sHh+cXl1fXNLQx+9y9fOAAuzv8+/pt8kWD5unf/Pu59/H/5wrnn+y8CyX08Ot4HpDJa+JbuT+n5Pj4ke53ws/oPAQO/9hm5lccE4TNGgQ2m839Z+w/O/scY+/T/irP/g7H/k69F4BEuDlZ5uCQAGLi9Y839QPhf8F/wX/Bf8P9HYONjE5WaBg7ZgM7rgh/3othZUhgYxcM6x0fcewEVuTe1b6DWRmRNhz+byZ+uvBujTUmmftZVDLqdIMOxi/oxV05AY5tBrCPkDnsLEft8+JXzWyJa4slEDyRHAG7YnFAmzwFCuM7h0+98xADWoKEy06Mb9m8ORKHTqp3Wl6MGtWlWwfkGOkEtceUdWeKCg5Au6wJj7um4h/25Q3lwXZ7z52rqkVQHLBjAuGxeN5DeLMDZxyfZAEe4p/XtWstHd6gnmtyonWU9qKEYAj4vM1Qe/wk2Klq+CuAY3oZlvTdhcw1dqtd3+xKQgPhVdYAmd8YzumLaLMmu9Ix7RdxUWPyVZ2yof8YANNv2Hak8S7AuLVWmCiYVrDrtBJ98K7qmbH+D8shJP7oyiMcAXQOzXzCA2UMM0PA69BxkjAGyzzDAWn3eIXlQ6FEyctwCWYws6+/YsHa+/3ZZDiZfF7r5pODvsv25QLB8cTCWznGyQXx8pFiEvwLqanrj/AECHRCPOCj5d9U1/ajOILGqR7yX9guOFFyQFhYfBIkDI7YhYTwleqDZg+wqOX9NWGhwKwQDlF30igTJdkgCGKBdAaZ1zZ53N8M/XVzFrwGy+IXIQ8MxwJHeN2SgV0Wq4reAp/EH2mcpmrPM+LlapvRB0ta3FXlIYgxgXtG/1Wqn1b5Suxxe4ucU/VOFRO1a7I4jI6LPhxR3l/HL1YuyX7A0lRxaU7wtWMfdzJPkudcphlKFvVw68dq1KR5pvFsr1cjDPt/+iwbhJxQQsdSM5bqp+cSo3gwXE41vjcneHKqkbyy1vZAEhN0XYONa+9KlVXaXS62FBoqCLwkTv0we5bt3SlxJFv8ynciNYnvEmhsF/K8IbGwOP+73cpGT1ZQrvxjDLzmRJtUx+lRiR4szyNyU5dnvEyCTLPN+ip9G+AM5eKXzPlq0El/rfAUFv6TxNkQ8EAF9ijooCvt+vUChQfJwv14y4Mi0tuFR4Y6KPdoo5ivvod8RBjgsj+4gM/kMbtGP/2Ds+XV+373zQZv2Zc/tpBRD82J7adus6lytacMBkz/VzJLgzKNH+sd7qcwaNoFMaz1EDuFrjXEiRFilmkR1t8LCa4SHEocUzhWv99jwekbIGTxMoHF7BybPVv+ZtcfJIP+o4b/mdjDbcKNL10w9U1BdDY6r2rbejtzCAB/24LslSpvBdu4YADRZhYh5CteOJzIxebR2lPoXQbuHAWg41ITQpI0iaVqtLW6KdyFRkCweZ3nxEANiay3o0Li/tzC/OT+kg1cQlEmxA90iD3KSooiE5O0L++LPqq3NRFz8bNN7mYsB8vz0F8G+JBjgnDm+HMJpsU3zh2tBWs0OsrNffaVXRtLDhAH08I5zoNIaV7kakS09EE4h/V8YoKn/zqpUCXtUUhUMwGWpAcMBj0yclErmweIXdMzU3ky5WUAdKfMgS8wWqNQiSubC7ljSSzQ+e9Wl4FhjdJAMK7weT+PWyuJIszFSsBCx2NaN+ot/VXDC4YNUGFQ8ei49Q4zsksYAlWmOGKBXpz/C++ls1yhktVUHA9QaPFusLGJZnYFigNM8zczh7jntVjeE07SnwQVSNjVhtSq8SsOw7urm8gtaejqimxQDUKcSYQBcCJq5bXbz8MRl29PfY15n1q7YI1wt3t+7yVf4scrtaSlSPoW7vyiHiKbDoRrr1PkYYNOB5pkoBojPBCEOMAAs49KNg5oqugP50ClgqSdgHAIzzeD6Ag29lYxXxACfzVpNDdHcWKHYYG/97KTpl6SBAToSIefkexCbhsM5sQ8YoDFJNfGl5PPMYQxQtNhxN53R448P1VCieZlTe9CPXuzAACQyf11rYw4iDk8wQI9BisBNKFSp9DtkahdcIO9qdcJdDD65xADVBQgMwNMTVBdviN0rZHsb0tMUzOiGZs4Tw+uvyEGhsV/bfix3nK04yR55Y4DZ/Oee8fCQaQVUG6Vvjz9uGMOsQoRrvFyDW8EfLJ+O3d2N7P6f+KHcR4PtK15iTmLxKAxQYKajZdFa6oSLXprardqBRScmHJX9GMcAUhggZRNrNLoY4JioY520avKEGD1qrtiyWvnb2/kcA7jglGzNXYfteLdOXC86WpAs4DMxTGd23xUj4tluuKh0WRTnrLcZYzHAO35k2ZjCl/qePsH0TNR+8kwk0mKTCcRcBZrA8t9Vlt2CYDUfSzr0BZ+LfkbeTIJuK2xBAzqQOjt51F1XEapmEAP8JNyhO2+MCic0N8LOcGzBBabxmzzRdH0w2mRILT/xnmyZTjnBzasDhtLGGXrL6WCrFIurB/Xl3s3rIg2tCRq3si7gqPr33ZumF9RO5lRKER4kjGiriiXY+J+5ctLdRRMCyWiFeBQBRDnCGOzKRX5ccGM2rjOFtDn8w/PzPmT8DQU4smxxRKXcMVRzEtpj0FBqF/7mjyiAjD0OCAh2/lTbEHXx6o67mvpgWk6ceCICNFT37rSyrrWei2rJ9Inyq42Iqp93UUO6JRrGbtrJh7JKFY9PeHr5eimD6xS4SlKmzaUJ9LVlDNxSpFncqaTBvqLbBjZFHqFjD8cZyLuXVx3fTSi9zD/w5ujp+cNMWNPUR7bjd/SJI0+lLFA8WtPOJw7G3jUcT6dchQNpbZV44hm1XfLEwNnwsEjKNjCTTEvOzgF7Af6Xg2Q9rtdocSpPhn9MavYqCCzeMB8/X/z87JX4wPorap7f/uDoNnfJbgpaSLJ7v4xCFFJ1SiLKZsxPRDI4zL9+OtGC/5dLNe32Dc3M/sY+K2JS5HDaY+KdnG8xgT33RV3scuNVqZuHWQsfygnEpuKxgD6tcHZYpM6oGJtoprfIMCKWA20GEp54aBnYsT/3oav5eFpoEuhgk62DZBcLxAB3R4XxclN1yUaCZSeVASZLNBpIohKkyG2umfJjqZVjAXJDa0TNirc9w1rH3I9jju9NGZMzMY38Lxjd2qAexs1mRrowL/kh3nBEFtu5sXGZXK5j9eLPrRHLNLcjeMZIjt505eBlYfqfYwsrtErUHuOc0n3jP2Hoy/ccUi76/n7O4SyTdChnKUMFgxKD7w1idgl5oj0Ep5rtZWRBgof2Ew+cU6z5kxBVvWNOBNkbIUc+x7zaR13i9ClskgszwpH01BymSldUTuUt0PMeNWxgTG1WYvpKze+pBY8JnJYwsNH+0ZLFcHT/yrAf+TDj8+GFfSgIdZ7RH7Vo9F6Uu58QGHMun5QCra5amclbVHejRly/ol+WsW2Z6i3hy5MsD7qYu4Z1YYBOOaN69MxvkYZPUAu/za3LKoWpNvGfB8oS0WT++Mj6b26Quaj5p4VC61u/ripFdz0RrJmyP3fW5rMZ+0K6fWEpGICynNu+rgUhidR+gwFOKifBdzNHUl5ByMJmDPDc8a9TAGPN597e0nTrEBjIL/ix2aOhIjEdY9JpC9n4NvzjWlxUt9EF7k1abEebulO3uu1ENKjtQfd1aY2iaiL49sufqmDxb/mKPIXx27JNSR/71IPxnIz3zRma4LMLuY9XffVQYrONoeU/wrY70smzQhRr+BubGeAGpnef7EGTbTF2YvnsYl53lKx9c9V/IF1PK4b8M8ZZZrUhBR61ErO3pNLrnAnVBjRbFYF8hyRWbTm9OJANzmkjgHAMBNJ78CsvukpoOj2f1M1aQoV5+dzkzE9HP0fFTMamQfGbK+GIrzVY+U+Ybw3dvqlB2RLcV4qqPoyazuFpY4PT4aZT36ytGuuVxNW+QSnO5UnHaR6anCzDbFmladTVf18YEuZV02P1NY8kRZJXc+Bn8nd3jSPywCTojehPRw/1lfM9bIAmTPEanutboGXEAE+QlDME/1gZ4YwqME8+1Mw7L6wmD4xfObaVzDp+p/fZnzr40L2mHVecHnwm1jDJXouEXwmyj/4T83jPG1yhZ/JKS+Nnxt9V+ucOBg5bp1FOkn9SWdvHfAd8CsUzpto8qQ1luwHp0gBH+1nOWyGfEV4DajPXnUDWmrZbC9us9SZZ6oTvfEmrn6c3wT6yMEEfvhGukNWdrlD/OF0hiE8ReQbPZsv7RKOF0eZPyJuj7PqiuVKu3mNaG+6Cvvs9wQ58bd1fGolDnK2PKQWXG0kaMsnk2ZQfhMu/hhCWgcNdBlbs/QWIUUsfmyG8xpwuaEbZH2ldQ/pTo9bCmTiJK3/GED6LEJK/c/l+Fps6vFHdPeLcXPFDSVuuU6eo7tPJtsMtjWmBVv3s/b6J8myLgaVQ97kDvVAF9lSdmOtS9wI9c8pXbT/zG6S+TQtEcnut1S1C8k1qqK0/ScbPNr1AmpUOlzulBpIuItSaAps05cvt6lcZvV+YPtBkSNohauIZbfqkBgpDSwULbTuIZaZzMcPpOCHna2fI32wh9L2BjuUmfnnq3wTHvlub/XFv4c2KCVY4a5yO2ksT10/dn5QoWfGWnJKb3pgVaKrK3bAB8UHHppbtkedRU1VSZ+qN9sxpLhBHt5eVKV4fSVkHpFSKhvhwoIDpFlM478B4UHnlz+RP+TZY5sUFZfdzo2T/p3fB/zdg8FWcrv2l91JJhHw3hOecefd9xYcHZPYFXlKcs3J1XGQeQHT314DGog1UcFmPd6zMKXeOc1ZeR4WPZYnFqr2gU44t2akrzYVdokKXvtw1BoBOrpJjwxJhHHo3Orrgwiw05EBkvKT02Zqoc7q68Pv2rtZKz3wjfqb8BwqiPhigP/5HZajRTHa3euNfrwu5kUianX69ZT6FOTjh5rVk1/n0106vRQ9e/Textq7MXC2H6+9Nii2M+3L3Ao5jGXK5Vg4trGNduNr9dd9+3+aykoi59FCdApl/ylBphSuqK8FzfrvKFS12uzQOLc/jux86ZxS4Ri4K3NWKcprLtPsLC98qALq5Uw5wRbIkWcpWoOnmQcXSwbliVE871cQRt0ezq96rIXAMpXPeCb3cY6jYzKDAzJ7NZAk+YkbZ2T/P4no0J0B0atk0lmIu9Dk+y6+C6oZE6A2HnzWfEoOL3svR5+/M35rgNFyaR5/tvUZI1jo/5Tllhr+972V+AsMAyrsVgvcXKo4rR3OIYcaPSekEimtWt3ZDBo/r6/QiaXmO9H1IX7FJNFxVcWt7+NpxXbpqsW4Vl+ipBx8OfM5R1mC0/675ZYeWdnsmcCB0fnnvqyW2k4nL6NieFn61ObaFbhZGf3L6cf0gHlSdzdU1u6H0seDB6ydPVq+t0Ky5vx02OK3GNDvMfpdxS8BhYzj9FxUE26TLDJCa5xdV5XlMLr58Gb4t4r+fLGNLbYWPtzVOyNTT1gLm0CcoyrXv79dGZj82vLuu+t4zfjvZ4Qv/tPDiiIJote2opyyedAX1HAPIkB8eub6+quI591/YjK7vmyQXg7Sw/7poK3fW8GRettol9iVfMpZYWxDKNNwasNgxVasahbwTQx4hj6avWm3QfTVw/LvPJ8fs56Q7ii2tDOmpBFnDD2hzdHS5uSrVFSz6Wks4rZLQRusIwngEO3eh2J5hckxyuf+F8Qo+BjBIONIad35f0fnOV3AfsvB1D2Wxoyr2hnNhXmFL40ixQCvb559wuFZmvHIGaw7jN0MDX1TsvYbXIfV0k7m0ISdy4PKfCNnxnXDfg6c4p9qO1coZWYX7v7I9LqNODVQjXCV+5hiXQGypeV/vf3jVFF+E6Cql+Lz9dUtSm/fa2652Wuja5FoSfJA4JxFueLH+VV60/7fvM02izFhlPr4OR30MMOCseRTwTnO/ke8dmNU8AvXTRL1UR4ttaLJ6WPrldosIZ5+0xo6+taOsJ1WAVwXoYR8PN8+iujoZ1mywTVLt1t6tf3GJkdx8+tBYP1Hg02FXre66dzIcSYae0jfa93B4q9dzLmd/a86/8eMlLCpxeL+20MZE/oSvHF9WTsKCs5JJ0Jl/nOwFwNprFGJrOQ3SMrsNDzJcTMgYN1x6f9JE1ne/uJtU4aQpaBj9twrMO2zpz1S+xpnQrKNDoPZ7yLSI+iJY8nHg9LKTQs4pX/F3L4VcmPamBiEsWvOsrqDS+htVFructyzDloeLVUWjn66kFNJJPOPaAt8vddbfQE6FwUGbyS8io7yIY4CQwBaeak71nVUU/oHmpb/HYmG0tdCy2UGNi9HMrwMqoR2wXBBKmNj4yiLM+LB+/df0C5vmd8cpY8qNxSyFG3+g73PbDv/eeLrbXR2y5Y/b5EZxMLzNjWIF/ueCaszfexNqLLiSjp79AQDOKNfrBzZPPKhc733XnQb0XirDvRDPm9733CPDM+vnlKa2CbibWZ0ZgHXrXDAYSqk+EvIt6Q4giami2GM41VGGdrkO7X2HjetbJq+qL9cKl0Ah/ObWkEA6Kob1Wn8n/NtWtMVsQ5tSZcXMdLbFKLU1Uc6W28b4VioG+DD3UnDikq8i5YsP3bXkEnyuCN9hgVqotZWlNW08W1ykKVyKTzx7Nzd7e6SQNW2bmscVzyAWWeYPgm3DZW5OlUhGPvEOWqIc3tVF+5z539KlayRRQq2cfo/sOppbL59o7XPoI6NdwMMayQPYaB5r7bLGXvh6q1mEXNB2mApP0myQHofL78V7OHOL4MO3emMmFJXu7lTk/K79XpJOV8L8Cs+hUn9LRUQ85CFjztGpu9A3SX2qO60k2gsDAz+V1gUNEHpoz3ZTSJvj+fLqr8O1L4XrhHZxmkMeM/onOPL9kgcV7p5I5SoYYWyVwnkPGYKU3Z/CM4+pnOZSr6Fe5nJsKCe96n29osuPqFXyHi3aN5rihJduD00UvDebdnF3Ghv9RdE3PvEowt+seIwGKXGZezvHbCo2Gk12MXeUkXzWFdzrHBHpkRDwav4eYnqK1fwzWrcL9oKhQpBZbeIVvuhKr5D3g9W3GrpuO6qPlDp/jll/tYepmTKd4st2R9K/7q4JvdOdqFwArxsVChuBV9ApYvGrIYLXV1aN9G6yM0EimXUc1uhbdJjJA/aBs5FMLyL3/5hJuboPII923TVuL8zdLh8iWR1jo1BQjqEgd5rxZ8v2sNwYDLBVf+RMx9GH/RGCARhscq67JNDyZYSoS0Uev90TEJoZG2OuZxSOzMd/flhkCj1mueVAlvVyns0lNKoqd4z9rup224W5DsQgq0/u3m7W9YnL8SunKjYcXD79hXOglXL0GVkK7bsSiCnHX0E6j/HWsMIVXrJJtHt+hM+0iWw5Fl/wD9zLGTAtsKYBf8oMx52sqMaNcVfDMwExgwn1if6hQJt+D9HLKX1kGL73JRcMu5udAy+DUzRnhTCAXdOih7kEZM3ZWBvNGKxAXsrnpYXOKYHM6WGAv8/yz1kZuhuLQJ3gK6b8v1HceSX8X5+PaSVhANPZgnPTm6Jug/1ahd95mg82ki65vOc0lngSPMzhoes8MFgH3DNF48isBHBvzClwXwVAHdMaquwQfrPaf0KsGy/Kz8E9zEU9r1+n9CvbrfymoKxOxgD2YGW3DHzppsrAGmLw+WpKdd4MnSxqEHKjY9pjo0ZcS3jqDe+rKInlcd2O9SEbNzJ1z7nV4YLN5cjHu7gL1uWEsLCH5IWao820elmHSzwNIjKEJcRDUudozIZOP6APN3mRigFoyf4m8mqHOSmqc4HAQjsVg5Vd2kVzoW5800DLMA+T9nGPGuIWJKgi4EFEq0lDg9xb13eTiuGnm19SGnJKm0GhgQY+3GkSoqnnyBi2dqOlPKlPk6d4OxnN3o5Cn5Y0NOVlQxhypuod5lL8WIxCX8/Sn6FWtiLS9ayf47+U1+SwTsjqfHTZGjNXOpcxZZI1kfJXS44s6v/TQlPaw2GcUVd9KJ/5WNxLZBRQkRMSIKkUyzEOBsi0lCY/PItyoP0gMyDZK/bhaQFLgDcZzlNmNNVctSAtBVmd5r239pIHDqVu7iwZEgUfN/BJRZM/ZbfhgUvIcCRqGLXqEsVyWZnS4wCawjbi/nb2y5R5oQU7qvMV3+AJGDPHXyn6o0ZK1+Sb1SDegl3LxWKjtrzhautOuF4H+GdVpnewtpr8jdH3dfFUItSaDNxA7aGzj+dMFmpar6mZO+/FmAqoym0KPuP3d5hPnpizU/PB7b2CxiH/OVy0URX+8hlH8YhL3xTvG0T0RYXhlOWl23jujGKfDUrNbHLvgnx5izNm2hu/mrtEOPP9U5h2mckPVtMYqOSh6ItMTg3mIo1UkX6E4OiX1PC6lGifXL5OAUX5wAonxkm6RIF6C6ZffvujULDYYCMt2HgplElj+LqSwHS/+p+UvBi3qUbQ6X2KCqqHGwm+GlaEAZF3kO9RtY9YfRLBvrTj5jnb6DqYuZrYlQIHyQtRg/4jmC8Z82zulNWxMVPykMZCQ8ohn8LWVYntpEBRnZsUwSMLH2lpLhC2xcdnmfY8Mkg0y/TXi7lC03Yco0QHrnXQo6aG4fqGf6H4VIHnSNHrcVqUQsBhdPAjYwXhXAeL+YCVuTGmKGfNCeUHuNznd1cVje31YdVcMy2BEqUcHOY1ddkLAgdkXPVjxgv9iraH+H8v43t8qui/j9r7WSVS9CQ0isiY6p1F5TcvLSuzq956Bhcm03kTuTPz39Yiy/ggZPs+YxODfr1z4URPQQemZoWFLAlGz4cfPfGj1pf//V4bWdOE6OClqU/skkn9kVQrftDm/bPvc+mKUjy0N37X6XsOicDlhwyzqb2ZZEis/0hakuqHZxJV97Xqt3EH7el0fFkKHH4lt5Id9FyxwCIf3DeWwQAf1TDAbOnJOeF1xGBhZ97K/NxTejWarm3k8p7Aa+qTQ88+9lTKDMhDOL1qf7pUzmT5RwRU0qnSl/PzzPdNjSOYQYeCbJyzrLkLxGgqVdyEKocb+PhhvigJKmeQ1hNwlQPR/eY+YWYA13vpJBq2zYn7zi/t/hMOwVm1ZY4Qvd1NxwJ9AzO14osWx8zhisMjGkgdtBYDmI3DZgisW1sTKt1Ue3PyE/c4Jb+UBagt+9Ctmsjw87lo91NJ9ir4+r3M+in/AnQx0Qgaq9VS+VmYxrcevq5OyTrYHWMfc6m/ehgoOqIB8cpvFnfJH/Lw7B8BK6twtEa+bNcMXD/PWKqJ6tdlsk1wWV7/FfQW8Wp/TSucDNsNzekoqKe9aSMg360tluMWit0jhKwbuc3WcSO53m688b09e2CaP7L5xm0YNNv80loBPZbzSo3sTOjhxfYj3TvI9ZF9l3FGJ2W3Zora9zYXnw0NGOjvpQEF44mVhZfl4aLXokRpo4cZn9Br5W/sa1Wg1xzCYw1o1GzwDKTv91PdlrqMIWdPRmFWsdhD1S8H6LN+c6RB1vJBUv/7o/vag89CZBsbO36zTdb+peOARhBFv0Md5SB2IH1ZN8X4StznGACn2ECtnSVaqeM06qvDYh5qiSj8jq5kOzj6r0HL56vUo3MitKC1fAZDpdHGDtdeJe7Ho+vi/gjBfos05VYGdDNla4FfoFHtdAXUbrLqmUCKUWRYPIDQGkA8CB+rrUVwaCnhLN00+ePmNNUPLys43y8tnnTtdNU10KtiwCY9J1nrMlQpvd50GfFKlWYA5eaITms4GwP19aKDA3nsirhuYpcSJVVrpjttt7+4x5rp7IdzpnEUnjcdBgCw+d6408R/YPOFBhKY6i0YPHARxQANajqDwX9PqA5jNzZVEjAAb7DseRT4PD+65+5Dqny8btv7L82Xzi9wguFbGKDK0K7vQLfWeKxs+VtGpdP7TEkxKiIva85W2xbvPU8IIeo5fILSCUFwwf1ZaHGmRzjRLPqArpnpW0tPpZJbm7+EDyhL93ez8HOIC/+LmIjbRDKi1Dvid7pnMDet5kbHycV3OGE4/M2/L+TxEaZTRZN2NVOpBCuPeyqp5WNbhykYEkUGWYrqncngU4raOzsv6tSIeHQW65GCZUqWgY/Ws86zyvHdl/UdPi+9TB8E7I9U9S+4u3HDkuBz9c5GHfL+NTNGNDNSCc6bwSZyKbcUNlEq+t6HQkGH3eh7SAMTtzxY+OqiyNtzl6P7W3yLvWwSGMD/ozUsydx2vYOEK3920JPWJNBfdqfj8z8GYNg5KPKqyuXTIYhNuX19ja/ma2e88eWR9nZKuRmbqFNWjNsxBniKMx5VNN6e9QScAsDaZ+/Rzwgs9V+31NqAYVs4d/qni1u3AjnvNKCgnlmJsuqG3yNm4gbnusIis++8dj+k4JR/Dx8U2T/RL5oVBL+qcWz8CGlJko1H+tlVmJkSVNjE4OnEPRGjyf2etvvGYLGIQaD56b6BQOLyD+9gwyrK4DPw9eoakq1Ie9a9NwUDoO+bQM4F827Gb559XcFF3ivRMQsb595VzVjNc11y5bp+uPCHxEqRQhziSydlUXJVvNST5tQaY5xYrlaznkQMNfFZDVE3+Lks8mdcebKFw/vd2XNeaN9LqhTa7Ve3D0pQiQt2Ro/GdOV2JGzRRiIMXKfhWHOdUdMx+3KTCNUTQ/949KVWE/GaNrmHklTVj4UWbij5sN8U5XiwyRHxiiwbnrgHtg/+uzHQj39rwfZnjPjnVQGC7B6Vl9jnnfV35YUW30JjSpBp52SJS0aDNz/cbPSyuksjMIDuUqMthMYdKge2penC7qTd1hG+O2bREKsvRwrnS6Ivk+/5WBcmE8YUcsN7CR0n1JefYVJxLF/dMzN6qyE4NPhU8aDxlG7h0uZp575BdRmNWvziM7vfCR2e20NhTV/fxuR0Yl0i6E733liPyZK8t/inG6iRLc8lSXxLcCCoeBS7a/dNDVT17ri2jYjmZ6ncTbi/lc0zBOH5hatDnNAN/q54nFL/47RedwFnvtVDd4LIT0y8r91p11OpPIoYpuMzC+S44jKOxCoLPD4ZBf3FRfWN+W0VevY3g5RvKfWzxM1cZ91eryjsDDyTfrj1Ap8mu3mfrZTkmGbRbJA7yOW+fuLAnG8m56WbR1DY8oXwi62patMndbV+FbbTiyv1VMU2cbjuDawMlnXbn4RxmzDAE3zxYHh50dlq6q0Kg1PcOdzW9ssUB4e9+Bjx6sEAboImpIursKBNMWOlM4NNmOuParPpnjXEP6S+6lcRil6yrTXzpp3342o3mrlRm/nns3mJYcXO5bxUxleL/X9v9/GEtc91fRe9ErsrzOejnRPITtxsWlMauYXxucJuD2L26GvUw/J3D9SQXQRzkRM+cK5GqjxJg4PJyj+PY+vORtIu0l/XmAaVPttRl7q7WulfpSksOjzf7yCG4d6ctghZztrHayJEpwsybOr0SSTr/JJt0Fcu743iXkmLHFxEBZkzK+F9Hvanqli3xP32vtzPpei26XFc+l7oqaG4y9ZHhmjdpviBJv4lIbJvH1l4MUBdDi+F1GrygfmYTlA42raxzbTOuc5f25rGxh5mkhes8FtjZs0SZT0yCyF7uOqcLvgyQeY9107MEitJg/LlJRRIfALN8W3wtNJ42uZh9to+ctSFIuWvic0xgyjuKLyFJjsl4mZAdfby92k6+8+oPd5HplUuw/Mx3jT5ulJBSm6P3A+fEnAVrLiwxfDTeyIa0Bdb8X/UwGVSXXfj6bMmsIyVnXqFLMbnDsb3okprrF90uzF0qNdtn9sl35yP726yMV/gkuaRel5k+4lS7P32eOzuat3yWY32k2e7gGGn0IV1quxStjvUscPp8zK8RuoqlStNEw4w9osSx42Oa50cKMxQ7YOMLsVFJXQKexpt8+nK+47ChnYFO136s79JBscqrjL8ev5pWgqewSP2KqZoJJ7R1SIzIcGU1LT8/ZLdpfcIvlv2WaVdfEKNzNrRiWZdwkP7OI4qnr1LLtAgVUUzvsO1OW/o/GZ8CZafSaiP8+aSI+WsAzRP6FajgWeF+Pv1UutI5zvcaZ+Stb4AVfdRjrZo6qcP7azwoctfAVe/Q45I/q4pRZWST7Y0NnSv2t+y3Ebv+6PwZKm/vRKo5Rx5Otw8whGd0vnHErUR175bdahoYSyJgzQr7Jf4++ub2qMQz/46GxawsLnCg3RQ9FWjiSZjoqxX2E8bdeZ+s7bLq0pA/OHUU2gqm4os3ednhoODX34ruA0lvuFMyrd7Iw8/OX8uNN4I4mlsnI0v7pFqGFeSYqrXGq3H5r9nI5AUuzW/RAVprwOmhuA18GJd2ZdQ9yVHs9+Sdyjnb+ipFtbW3K/tE00f5LeOVIVvI3IVwWLOeDQb143z+0k9d/FpdeO4SqjT4+heUCq4wrThnBpOE9iz1aTCkYx2co51bt2asEEetNsifC2vnSBa8e7BHmZx236Fo0YMzpmCHgCzIw1dNjYzSQYfHot1DbO9iRPNhAVFR66B0x+0LaTuf3oxRxNWSmZfm07PJ28ddLwXBl4p8WO9+jrLbWYV8GOmYrjcg6mHT5ROa+Pd94C3/zhL0/CbQ4oO51IRlimR+lvDabvyNCkzTFftqi6UpwwoG06PdWsY8bn1i72kE1Pv9xeFYxl6efxWUVEvrLOZUpmfxPA9LHF++t/9t6wwaaCgcNsVtwR/rgAQzDV4u7ztefLGwSDNZSzgu+6HtwE6Rilktf+QPUoMIASI8LRHpAGbpD4OKs05q5qvuS1QedR6yBPepanDYDHq3WoJjS2TwHvvjrfXeDdWwKHzgYi5rOFgz2J1c6MXjaTup4fBar6WZ9olpxpv3Gd7iwOrZ7LjguxvviiG5b15SVy1Z3KnXp6R7Ppkgt2b0I9h2iDxXkIPgeV3r+LC36lMJD2wrzQdy2CkQb2LCYGa/MH8WCq9q77T3q/DgOz0AvbhwPdfW0HJuJcdv3CTtOcP9W9vNh2+6HE1PnkV3FRF3OSIN75Y7zw4a4B+vAS1vVrWWLZw7VAOhM1uqVmwaHxxkaFOTvLMuc2s8OgmEM3LNYzsuQkc1aYSpssWxPFQTXTZo7WmblTN/nagy3Iel+VKkdifLWyJv6vmJ7j2xZsq0ddUZBBNw2+EARz8qbxqRMFZXpyPDHpGstk1bALL10iv/EJuKDDALzg6JSHw3PUvm4m4EREkkBYDiF3IcEpDShLai8gSLfzfMr56zexKBvr2cXmGk4upIuyk8C6rBwP8k43WdqXUjeK/faY20j81oVChn9ZfSQb3UXi7rxqB5EiI2js+/1D9ugm6nGE7ihjFLfr+jYGCyJhd04zAI81Ttk+KPnCNuDOmf8zXOhTJ7iGGen5dJeQziOJwM0rJIHu9oMf+/My4yzrJqCn/ipux+gNtqs5BfUhh3eO8yphMmccMbpZxKyWpNxocS6/XGW2D5tysse0TOUSrI1zFJnyh5uGiZLKm8LZVuSqDZ/y32LxDv8J28hmZLRcjDtTmalltdWnlwrekOJES9llORj61W7JsBeUElbqTp/KdxUR3uouSZw0ZcsutzBbcb1yFuWXwpZrJD56ZCwZyMEYc61++o3qTPt8TuFUFv5vWKzghdXAvzr2WuFntO9+m0asbkdTncw5ZU55pgzGFqrfR0j3JVlnHADV++xDlw4geqr98GcHFWM+cn9Y4J9J//1rOnuImXjCxq71X7JzqWXpIiMVxZp+8TrMZuU+DWMyvo78onJK9M3RZoON2Frf0EMTnlPNtvOpGB+F4Wj/l321V/Lr3PNelsVsQEpFN56puq6m7EqmFl4I5Ycg3qe2y851Hja7GWOngSLBtQ3SMhVapzilNyjkbaPH6tn43nRxMtkEhlM4fNlUWpjGA1woAoTPy8OvQSzsVz7ktstYtZpqWzEuTnXZDEpc68VJATysYVKFdCjE0zbsaWjnjs9Wu6BeOjWk0Lrul4Vr9Q3qQG2tzf+Evgvfmh2xQGtfFmYYdrqpDUlHsvxOhhOq3ildNSNwfxtezNzf9mSCYdsdHJIu4W46BglThATh3Lg0DOK1Bxvu3c9MQyhgAdH7NRBgjm21fTHzf74kgVVXC+dI4BsAr0emmwQmFrhAjDmWRZUMddW7VWGRtnZA1v+7MNAFUMt4o/1xHDfJepPByWr9LkvCl4DCs8LIrtcHlSUQRsWTHzsZMchGi1BBt1xTq/X7FDjL2047ToyfHw7FYDm/7ygon8hu1V8k35FqacVj7xp1uYgxfjpbxnygF3w0IqeOE0dLSmmMDaX37zpqEZUypuv+YP/mS3Cbo/kAHOGL9MbrrNaTAL0B9kEqe99K3uNtztlIrppHOkysd2m9wpoTIoM45I4/UFIQ8JG7dgMejEFVP9KUKM3ebttyRh5IxuBnB497olbMWj2yapEtl4sg2EfCuOQRxl9smPPYetjp/NylQgdpFHv5OxvO/leyElXW7f8cAb7fQq2SaQe4b09QOQ+CTizYZE09iZVw2xmw8sK3G3TuDHM/F8Z7HeBrD+T1SjRVqYBIvrSnlUAyAa95mOJhN9ojYKYDMdqcPwi6ZIrUWTQxpPi7alI8B7z53ga0qocmmzlkUMMAPs5wtdzp0yhZ/8n12m62S4lCQsWTWf+KfnLMonRQcrEUrOuL3VPAwUNql4iPi1PxmMUCARyNDRshYjltvRMfahThKxeTX75lTb4p6Uc5sqPQJGcdFDKsFdK9eWpDD9Q61ALJA9zUNUvERF9CxDFtUCKqnXfwU1oGnLz22W34iiBgJ5P33Ebcio2rqLOP9JPQEBiDc3JLIUHB12C5AlkGJxuHpC8MVjjXGcB5PiS8dfiyMoQeDpVWljvaM6WtogCOdgYQV6TjAR6HH2g03WFbZRdu5vtRR1smplsjOjAOnGGQaqYcMOyTwoul9QV01VB/V8DMKhhpknKGDKws1I0rWg8y56SrdKYjuhOsifpuAYAftVzKnsjOGPtUl+avv2LH+rdhNh6YNiO/PuGHwqXBxCcYbvGD84mM9Rz0Xajxg2eSHwG0K5phBPg7G2431tL0pnoTy7y710qPQokto8icGsWuvqbk4GArMzI9jkDFS+ZDj6Y4lYekzrKWvYfUQVS56WvlTyiCJkvzQKHBGfnoXzbaFv/hUZWHtp9Tkinr6dVmhdtEwcLsM6cuPN2yOYop3TMKtPDbgFBTVUJKRwqoElaLCNf23VIXhg902MY/71vlmWo2ykmGBVlNtAXoBa1HDEpAlZccZe7d1DQS0OaEUbG+BOMcAC5reSmJf/n3yEYL+7XIc1MEPdt71stfC3kEYAkEFyELAtzpItOAYxEkFA4DfBGPTytEEqoQHiepAwUBbCtXBYSdPPq+O7+dg/d386+o4ahsDtDtno6dy0BAqNHISGwWWcbAerQ45+Rcjp8by5PFp/QgkJoQsfFMHaferr8odS5kLA4T0gpaeM6DNNVAI7CZTN+9M9xcu88E9DnzCZfrgm95BDJCGNfEQDHB3BXFesUdB0LL/nuZ4m3pC8DbnzlH+AhIua2SxeGtxuQA5DVW4KcDaUuoBtpvLEGXE4vhCpl4Qbzpg6WQTw2cNbrL+XcbOgiZQeV6QnVKsNsia/0X8CL48hpzmqTR37E3nwEjK4xtXMMC4HAbo8KJCVMH3c257qRNBfELCwkh41aYGbPLUDX4ZfV1ucUKUc1qEQuQjgidOX2CAD1oD3VlUJmvooHVkx92Vf+JNQyPoDMeww7nlSgOxrnUzXHUDOf2IJvN4tSeEPEqYZMVHAlq7KxAPOmyQJ4/khsZjZRMUZVG3EoABtnLjFLap0YVz6V6QvW9IPKpKrKTzLspl3b2P7rT2ln3BX/MSIsSEav0gO79AkflLXgGjGCCesJdvKACaT8yC8AoUXhZFxv5Oe7mHAfpLJJpbx8CnLb0jEVXpKtXjjmCxoGzL8W0Xf20Q3M8CAc14O26SjN0CK+/rOIZxPc9rgXABrOxc7rSOkd3pN0IS3z7CK7HpqL1U9KRip9ELYeO0bftw7/FiTW/7aStRhsdCq1dj0pECPZTbfn51kid7kxU0SsqjEBmnVT3qk2G4FkjatEb14A+DZDx5jwMW/VBToOpC9VH5h4s8EUuUs/ys0CSaZanXMci2vkXek0qlk0oDZHppqtdsNm0h7zXVUpfjFcBJwGj5eco/xsbqoVmTdogW7NGjWxT7qG7j40da5ZO1Yrkcz/ZNCj2Xk1DsK/4K+fYq3PmCkdoiDC4S/ZeDrU9AUtnf0N55cmSA1n8TWGSlCXLMWRkYHo8L0vStPnEP7ZcsdQKUL8cjzemCBTJVHL+N0rM5NC3msTy+Fj04fuwlxXDukhpqyxnTpZR8bNivhv48F0M0eO2ibPb6JLq1+q0kyrkVP2I3TSI1crtnpmYnbseWGzrKQHoyOK5jcOJ9/4uPvzVNisfDGYUMrWD+uOQveVx/ncMy8F6LrNBqa1xVmU2H1UvsqCvtG2bM3lBFBiHsjVjMzmw+tUrK2RzeXVcmjzsXSsE7ojZVSdt/BCKmW1Y73Isc/h683rBJkeFc335T9AsszTFWySw3Mtlsteb1pMJUqw11kKXG5Nc54dyYrY12tHNrG/FnzldsNxshAJvlIZ2lxqwpLqFBTTog9me9Ymp299yp6ioOKDMadcn53/R02ho9P2Muq6upUgB9KAW5tKWl1HWir2Lj9zTbLpqlXDYxQLPb+JHWCeE2l0bwzi/5hPSlXBbmJPfQvVRdA8tLz9vgMNv6vzHkDRo8kjYs3BDKkh3Xwe3b7cmbMA+qWH/HmUqFQ0fjzWWjtuKdbkvdO5r6D2/eTidmNSTkJt1mggt4HObhnGKHnvQ/uL57ai52uXJbRxfu7h1o2YuQ/7TJXVxU6T+6Zbi7m463CpbfT1dmAWLcD3St/ohnhpH1Bx9PCockzyRNb0j3kzMxmn3SENJ+IrZbovGRX/frK9OWa+pHf638VUiJaZK5wm854urpfOJpTJpAxguTAgOuDJA6ue9Xwx5SKemebjumisUV9SYOK7PpDHgjTbvY2N4eayKW1a3w61e/q2ipkhvbtvx8mf6EyqOfccsBvAWB3kTESlAohWW+xM2BSSMpXKhGSpoOYjwazvaWbuSjgfivvSiT1mKmaJtJqNb4QAXK4eaXmZLX9h3FeeJFqnVOhbo625G7VUXkpq+bWjfSUQ3Bs/xLC3qSc2AkNiGkaWskw/9Id/OFCbTn5ErbSVRwqQfCLRBGHFymJVUdggwu1IA97FWpbCX7MTxYtNqhYlQNzdcNVW07fYDfWoy2q46dWY7gkig6L26foAOHWEFWC06QoQuZ2LRhoNDGLrkng3Iczh/C5zeORzg99jzijFFc41ZAyGczfoNQ59xOFJysWV5QrS3ErkLng4lAqNQkBDfvLJr3Knb8qpxHzO4Q2/VmW4NO/x61/zkePeB6NynEU+xzQlBmLpdRYtC8jA/hDDWtJTX4DI5VNn9boOcvqWH8jF7xpcDo1oPv+KOQRjQuBpjLJ3H0wwBfIw5M11LoDosETuLjUiyMvv1OFONHfc3LkkYTqT7ODc1pxAb6kHGYgYS1jyQeS/KSey9PuUZTIGsWbfCjl2uu3zDAEj+arC/nNeji0qN/AXw387H+7IH0vaRh0SOVpfEmVLLaRGD+PR9URQcdiq3DdbIjnKMBA3zkgemzl3HYaJ+ISvrnLU1Deeyfmq4dlM2ubqHRxGc/nMQ8ruqasJkjFMlB0bN9xq9OJPYBX+aQDeGU1b0gPSOWnZ79DsqPAcwUYNqxGqoYIEc8HoEEd9WYs+W7jPGFJBP5Xgmg6s03jtedH2uorIyG9aPvE6OZswXNGCTmTTHAujS2fHKmOp4MoPRYUsppHaWZLQ4UoXIpdZQJPyIqx0qo899XJcQKUw2iib5iU3HORwzQM8svy+bSox3JvCi/+hjsbDAOfV5b6BSroXZ/c3IdsqSFJostPvh9Ugk+xfY7hINC2Dzuk7ykHFBBs9h4FXZ8kImvPTUGnqjEpw7azG7JzvwUMuwR7E6PAcKsURnviJOK6kVM1HG63geX/q6AgJvMx9KLvSUZsXVI/RoKZXFWQBmeMm2CzaprvVjyAwhODLCcd1yLc+uuUF+1dwvpJLbXuLPrdjJWQvw1h/wHEumtQkiCeTyMdFZ4gelKIHfyrQdZfF9OfRWK9sarFc2cf2usfpXK3KpdhGdEtqOxZfysJTwmhupEuDg46Gf/tnNW4mjbj6BOo5YYa3KKj0OfyNDeTwps+o8P6gIkaITqvtyTKpAoBe/Vt2vsaTfGehUe+UjffIhHpbZNDWYWziJ77xFAWiC8Kov6JzCiBR3JF21GBUoD01CdBR2sFcoUdkS9Mw6EwL6lbwLhfPcK3KdYqOeyK+rWr/5NtZSrIZ895yqE9WtqIV8D2fWrD+x7W1gP/AhutCEF/Oinj8mIYfAgxGs1/6a6Zkk68LeCZwbgZdzDzfqbmTWNznhrleYD/L6MV4A/Vg9rodhSjKAhBryTX4Sen8sMjnJ7gw00Jdi2IQ0xEQ8jyVu0EsevyQ0QOR8LF4MXoRd0OjYk/yIYc26P5zIh9s1HAtaXWIFaHJ/e+Vv8eUw9/2E7P4AKdik/TsB7QzJJDHJYu+yDIHbbEAgJyPgYZB2ECgDXTrWdYmsRyPXBpRW4DJ+J4S/V5oO433TYCqGTnRkWUehT/Q1NZMpzE2SINWaW9dz4XzKrShBl8KI4WmZYoXqFONLYIvCFJxqbDWJBZ7/qKm/44mH3MMC5XjcR0Tv7oJzb+X8P9WvR95IYVQfa0Lg9LTZOs24G/XNVOztmeRULgZUSx1/lYQDuOdDtCXa2ge52WaDAOq5ywEF140p9QntMXw5XyIaTWdwc+tmTdAwg9Z+Yse10WOKPU/7cdsUfmZY6eHQsT1aCDqjDy1nCrkXBM7CAa3RqTYYoB+RVhzeySDqEfuGmOgd9p4X1x7BYFywhfsiaM5o8E/QJiXU3z67GfvRyPva4taAPbarzDF23sqgjU4hYtnHOmLgOWrsfyemnoUKAre/NDJBsCj3Orjf8xAinDqSaQBD4XEpGCnSB1eOFATzDF0kbQmuaVlODbR2HvbGRteRiuLwXigFY8zYFf0gsLIeQ8sB0MMCGtRG2BM1aQyE1zgqJ7x8O3+5NYEURqNsIQgiKBjF4RNxmjEc8PSqVh6Q6NAbkpMHD0i5wg+RCYe+4NWZt/+2wIjYp0I+FsLTcQKgwDQzwcFoJXdtLQy17EmACZxJTe9a5BNfxG5e5+DM2zc+LIk1rRW5hGwPl0E1qONyrEWkHRqpJwNBXlTtT+IWPTtBkEbJnu8sdseUGc7blJxigJqrWeWP8sRp9n4SNUWZRWsHQ2my8L7xrHK7cvYl3A94mJUY1up2VPO/PSPJExfCevnfquXse5pLPuko3bdfvdzWKZQjkrpjhG3ohM+3deCd779936QRONeA5W2jpKbQuttwn6MtXQH7asKj4k29BcVgDSuwaB1/PjF9XEEmC/8w9V3L95Zfq6xpNEfn0Tn8s7OwQurGEUN5dU27Eh54aMTHsP8HT9rptRSr5mpGMEZM7r6hVRNKcsmAAcu3+zQrvsefHRIc4XzHA8czhs5wnSJBLxCXpnXnXxSkuGFrJYXfUneDUotpAsnDAXiCU102ZBELUZ5ap+SKGtDKDpbZ6T69RxpsT9xu1FH4lSo03G+5Np0pobcSqlSNlLb2gnVxDz62bm8YlRcEy+idBTBXLsPL988VXic9HjtePdY8XbqtMpoLEf/ip4ag4cAvSP7iltQkGN4GzvJTr6J68qfIk0EreqUwVsozXbG6Z/pHC8Ez7IXrEs+me/N67rZx0bJbxQq1yODHafNH73orzqf/3WyMV7xKz2vR8Q9hytVIdcYFzxXd3uZ2+Vf2tGRGuk6Qkc9UtlxcrLyy0x1PbLVLld/oeWn+Phxh7FOsR/gAeAC9Lqt/Qq/3M+r3wRWD3fR6n9It+wQeh+6XP4x89F/JU4mDwz9Zm3d9pBQ2Dwyx+3Iti/b9CkmhBIfvXY3XRH/h6JkcDxy40/opdcTgig2V6W2tP2ww3qNTqmwzkJci0297as7D40q6vu2f/Vq9zFEvSkvdmGaT6nvblumFOMJ2ST1W5hxnfNFtjOqPiJtQZlGxAFYyYdSmD4/mQ2ro2FbQZMbSwypgtf1B3XvtslRgvO5jppmO3pu2jL09Lh5gv7A9qfF70NYEeyvjvE+ZFdwYcpYfOji/Cwe1+XNkrhxxlCwIostc9qMJj/CRUMpq8UuLNdMEgKH3qNTdHOjKqnX7acvracfeLrZzPBu650fAj2/tT/GFjOHacJvuSbL/ejP2ZX+ddav3rK4Bo/ptY3OGHJ4PqwQBPDRcoKwRoGlOxjWZJrYLb6fBgrov8Rto9GVDN49zi4k6WyUK5ob0XP8qIL7Yzdugigntqgn5q2qReVclMop86Jx7sOu7W1iWEBzUX0mUuhQkSd81zGRi1tSXRBLcxDIJOqZ+ad7hZ2bfwCTTZmebPb73Y9z/JqZKg2VDWN36yQpxzjQEeOYk9/hOv2eBstw5l5OPLjnkRCAroBxSfMcV8v76tcoUlVR6QrBrB3tFmQBVfMGW67n14r4MbV+SLX11FWRdpYl73JhFgEn70sijhTle+oKsr+LMs0cDrEtwCzSZ4rrQY7fZdkvFiTCtXJPqWPLt0aqDbQfH2g+Kx099wozetyAO/WNG7DJPh/KxEkbl3iiIWRzoqT4cYGiKtBCi6LgxvBX/ab0R/kT8IanqKmCPGtvdB1/l7806SY35Ze0RXm+UXnpEMuMPz+OjR68rvDi0vq54b59eQIJ+d49zV62dzPRf5tApPm1X5AJaulxj/qS9PrSkW5wdSTtHzJbXBPb9XScXBpz5PjQF+05W8nXym87nB7s5m8rY1PIxHUPetak406CxfO86/TbG/OKbxqmK+zkD2Yl5JRSpNiJ8p5sMTFJtbK+635KwegqyIyrGOCgNq4WGx0GsO5NGPQOmKi7aEnNeyEF61QAVveFsR6ESu8foFWu9J1tDuK0pRClcpa2JNX0KrfiJhEa1DfhMWBR+mxGf3IWQKyIwqruTzrPKhcdTC37KQYKeXQlG7qlEc+Lhe/K40Pya48subAr9K+koKJoqgje439NyCxHIuYTOZgVT2ZpOqo1BQlPL3b6KMuiomfvHj76n2C/OZR8Fh8+h7dehuZ4pl2if4HgvFNHqmnCBabFAgnNAMHvDWZg8lQaSqru55K7CLe24/7C+6V95a650E1pGmJWktmqywnPMws6D/qn+lBZuOxm18Xc/50YLO72rzG4FFBdgS0KN6flxjfUpo3XkQ02icNmqpONl8FO/klCxOnP3m3qvDIdOo6mC7VF9mOvqRVxRiqX/wjzSLSJ94jgdU+6iMfRByJ4yfnv1apD7+mrogeKiTbssBebArAOps+iGvIJCfLVKmGWHpKbUlFDdQtyNtiCwFE5o+VX4wlVGpePOc/+lb2jNcn81k9q0f+VxJKhopPuTzrQZkZw/+HGXEldPi4dcLfE03fy1sTTbTKRFFdQqqeMleHuYuvfsduMkng06Hs7woyX1LlaD5VF2/j/2zSv8IflWB5MDDLLZcrfjWu4nd86E4VvLPjHaflsJ54YSO21Nzn4/iHF6IxHwtkiwJqtHkhl5TNP3p24JruvJir3rMchEU4SHnhYo/1fk0KliTSb5f3RREWZN16T0cKaJVbI3YfPyKgjwKunRxN7MirvF72rTX0t7dawUZmX4Of88RAvrfAGhAl78VaBYW8YtfDkctyEG6e8YSnd3wGyoH0Wqt/wDEfU7lREIodijCqxZlX6KCFH5VzzrSW0TWNNPdnReH/CVtDpd7Dr7wWs1wSqfOJHjHbKpuxXnd5bmy1Ge1Z0fy2K7k6Nz1FaVt4t1TMhm2lWXCiNRHtP4Dn86x5WZn8xmJYnkk9c1jT53eUkXNxVkgYHPFIoYnA/Wne9Rg/vCPUVrcixN5UoUnjA/2xTFyzfWlX2pEzvB9OKb1VgWjJAwI5yOKsWR083af2jJcJbc7mt0DPn2zVd12sw9DTOKu7aFazOm+0eA41+b+33J/241z/wCO03+0PAqsV/s3XJGHPN4i/wDslcvMgNq7AfMmHFK4Vbm2kAGJEIPvWLjO/wARacex0h1vwUke9PDmouPV9QP9FoPiLwrG4RPCBORx5moS/wBDXNrGu67gxx8xX8RkU0sGsYJMDcrjJ9iMUuWfWT/pjuux0n/CVaEFcxeC7DKdRJczt/7PSHxlYLsMfg7RAHwBuWRv5vWEAPt/QbZYxx+hqARubGWPad8D5xjkbTzScJfzPr1YJrsdKPGxEhjj8LeH0YDP/HkGz+dRnx7fCESRaLoEag87dLi4/NaxHBEttcbTtZShPbI5pggcm7tghycsox2xuodPzf3sal5HQ/8ACwNdWZUSDSo9w42aZAP/AGWmH4i+KvKkZLqCNoyQRHZwr/7JXPOHNvb3OOFbax9MinrE32yRCMLMuV988U/ZXFzWN1/iL4vDJjWZVR+mxEXt7Cm/8J54zklaP/hIb9SBkbZSP5VzwhkayA2HfCwLL3A6dKsiGTz4bhEZkI2MVGcemaFRi+nYbk0XpvG/iya3jlfxBqIGdrYunHf60yXXPEbyRLNreolJlJjLXch6HHrVVdKvWNxbLazEnLRnYcN34q2uh61NFbSxaXfs0ZIYLbvkZ/D1oVGPVBzMoSajq0kMryalds8TYbdM3r9ajaS4aaIPdSssinGXJrfTwl4hlubgDRNRaO4UkMbV8Akd+PWgeBvFMlvH/wASHUBLC3KtCy5HtmhU4roLmbOb2SNFcAysXiJ/KlMQDQvuJSTKke+K6tvA3iCKWa4n02SK2kTLvIyqI+xzk1jQ6XLIsVsD5siSfKYhvDY9D3/DNJxgv68x3kzO+z8XMe8lo/mU+venLaPIltMitsbhieAPxrs7fwhOshnvZbfTg4AYztlzx/d6/oKvR2fhXT8M63GqTL3f93GPoOv61DlHogSfU4eLSTK0kSM0hY/IIkLmt+08BapdFH/s2RAB9+5cRj8uDXR/8JZJbRlLC3trKP0hjCn86zLjxDdTE755XJ/2qnUZat/AcNtzeapY2+eqxR7z+uKvppHhqADzLq+uiOwwo/KuYN/O/Tj61LDHe3R2oXP04oBnVRv4ctj+60qD6zSsTVoazaAbbe2tV9ooun41yi6ZdLy7Rg/7Tg1J9nuR9ydVPquaPmB066lI5/4+GT8NtOS6d+skjgdwWrBt7K5c/PqEqj/Y/wDr0T6Ten/U6nOR6Pj+lF/MVjqPtPyjajN9JXH9adDfXlsyyRQyoV6MEU/+y1x6QT2vFzqvkN/DuTr+dW1vWiRceIFdv7pXcP0NHzD5HZ/27fSQXED3M0f2jG91ZopODkbWU/L+FVYLfWLdS1hrEzof4LtFuF/76XD/AJ1zy67cL8oa3lPrGWX9DUq65cmRc28Py/7Oxv8AvoYqkn0RLa6s7bTPFFxYFTqejFwCD9rsJDMi47mP5W/nXVweIbK/i8/Rbq0uFc5kCLh1P+0v3hnnqK82ttVWV0bewk/uSnn8GHWtU2VhqbB54iJhx5qNslX6MOo+tZygr3ZSbSsjq5fGOm6a0n9r6hEGHKQRxl2z/wABz+tYF7498OzvvtE1M3IIKtg4P13NxXMav4OvYwbmynW6UckGPDf8CUdfqv5VybXqWN8jXySW8rnCk8ofxxis2nGXMtDVKLjZ6neah4outR1W2mQ+Xb2zBox0Yuxyzfn/AC+tev20wuLWGYDAkRXx6ZGa+dbRzNJCQ+CX7LnPNe7+F5RL4etTg8AjJHXk1lJplrsbVFFFSMKKKKACiiigAooooAKKKKAMzW72Cx0i4muSPL8srhj97I6dRXzTqt2dT1KWQDjO7HZVHQV6r4nN14tv59I0nUHvER/MlNvkxqjIpjXd9wNw5znGO+4hTxWrTeBPBc5gvbmXWdThUo1lZcRrJg5WWXIz83GVwwxyp6V2YepGirvdnNVhKo7dDD0bS72/aW5igkaGEBpH+6Fz05PcngDqT0zTNSuIRI8wP7uJdzbuefSu70zxTcax8M725kNppsv2qKKyt7X5FyGWUhT83zsFb5ic57Dv4pq2qGVWtUIMYbkj+LFdCxMmnJ/IzdFXUUNt5BeakZ5/9Up3sP5Clkkl1O/Lk5Z2wB6f/qFVXJggWLPzn5n+tV1ldDlWKn1FZw01e5o9dtjVuZY43KIfkjXaPeqijJMj/ePQVWX5n55q2oxhj1ptgkI8LgAcc8kURo6Z9KfliaTZ6mpbKsXdO1W80m+S7tJNkq+2QR6EV3+v/EjXbHQLWXTrG0NvNGMX8IOQ3cOv8LfWvNNgHWpoNRvLFXW2uWjVx86dVb6qeKwle+jL0tZkvh231HxL4thnuZndpJfNmuJOgUckk9uKt63dwXvii+uoeLbzSI+PvKo2g/jjP41Vj1DUZbWSBZ2jt5DukCYRW+uOtJFbxrgkbsd3GF/BacINasUmnYGRr6QbEJUe/H51pWujsy5ZWk77V+VfxNQJeLCP3aK7f33H8l6VFcX89wcPK7e2cAfhWmiJNj5LVCpube2H9yAb2P5f41kXMzSyEGRtg6bupqERyMMFcA+vFTRQQoPm3u3pGP60rhYr/MegxU0cZHJ3H6VaSCRv9VbsPcmo5fOtvvPCvtvGaLjLMNyIgNtopPqas/2pdkY/dx/VsVz8upbfvzr9N2f5VWOqwd5XP0FJtdWGp1QvLo/8vkOfQOamS9lQhZp4+fWSuMOqQZ4eT8qlj1GGXhrlh/vUrx7hZnbCaKQZ8yOT6OKabmwhk2yIu4+qZH6Vy0BQ/NHP+INaEMqniQxyj/aAJ/pVAbWy1uD+5fy/YGrRsro23yyx3Kf8850yD+Nc/JYXMuXtJV2/88yxH8/8agTUNR06TazSRH0PQ09egtDQmt7J8xTWj2bdG2/Mh/4CeP1rPuPD8tujXFsRLF/z0hbkD3H+PHvWtB4iSWP95GPPHfs31FTRalZOyt5D2dxnIkiOQfqKLXFdo5hbh7Yr5wGxvuyD7p+v901cUQzDlF+hravbe2v0Z9qJM33njHySf7y9j7iuZktptPmKxhmReseeV+nqPanrH0Foy+IYQMBF/KnbU/uj8qZDMk0YdDlTUoqk7ktGPIoW4dcY+Y0pRSelNnYm4kPT5jTQx702EdhTEp6VG8PpUmSaMkUXKKUgZATjpzUrZEzHFSXAzC30pGHzGnBaiYm72FG72FLijFaEhmjg0YoxTuINq9KNg9KMUmKdwF2e1KFI7mm8+9GTTuBGR+8xSyLtNIf9ZSyknFMQ9F3LmnbPemxthafv9qAG+WDS7BS7gO1Lv9hQAmz3pNlO3+1LvHpTAaE+tLt4xShhRvWgQgTnNKU3HJpdwpN4PSncAUbQQD1pG65Jp28Y7VGSzn2pNgkRsGc4FPjhVeepqRUwKfiko9WO43bSSLmJhjtmngUuBVW0sSV1ORTW4dT+FA4yPTIprdPpWD2NFuSq1KvemLkH2NPB+b6jNMklm+Yo/wDeX9aiPHNWyu/TA46xy7T9GHH/AKCaqGqjtYbOht4vBqxD7TquqOzLiRUs1VffGWNLJP4Gjtlj8/XJ0Rgysqxqc9OpH4VzyqpYcA1GtupivIe6Ftv86hxn/N+X+Q1KPVHRnUfBcdwrJY628u3qbmNd31+So/7a8IJFKsfhzUHj53K9/wAfolc9IFMVtcAfxYb8RTkjUXssRHyyKGFTyyf2v6fyKvHsb7eIvDoWEL4VLAH92ZNQkO38sUv/AAlWmfaJHj8I2PmEZbfcTtv+vz965kYOnZx88Tg5+hqdyI7qCXHDptPvihRb1cn0DmXRG3/wl9slqPL8J6MI9w4ZZWCn8XpT4zmEyIvh7Q1IX5W+x7j+pNYQjIW+gxnaWK/+hUkh3QWk45AYoT9RkUcj7v736Bddja/4TfU1ikMWl6JEwOHC6bD+uVNK3jzXlaIINPjRs7dmnwD8vkrFKMb2eLbgTLlffIqERyvZqQjFoXywxyB0NHs/N/8ADD5jdPj3xWxkC6gEdP8AnnbxL/JaYfHvi4xpKNdugCRnY+3+VZhjdLpJ8ERTKBvxxu9M0yOyuXWSx8p/P6pGerdxik6K6+YKbNUeNPFYudj67ftxuUNcOR/OqUvibxFNC0z63qBYN8w+1P6/WohbSvLAxG148q6kcr9a17Pw+UQy3LrbxSHd+86t9B3/AM81nKMENSZmi51m5lXOoXbI6kgmZjmtOw8P6jdIJJZZHjz/AK2Z9qfnnn8/wrQS5sLEYtbcSyf89JRu/Tp+efrUU17d3sn72RmPZV5NS0m9h3LAs9Hsz+/dr6Zf4IgEQfif6AVOdcuo0KWUcVlGRz5C4c/Vj8xqvBpV06732wJ6yHmrQh0y15kLXMg9eFo0QamapmuH+RJZ3PUjmrA0u9Iy+2IehNXW1fACR7Yl7Kg5p+5yu9wF95Dii4GcNJ5w0wP+6uatRaXEgy/Pu7Yp5nDHCeZKf+mfyj86pXELzttMiJ/sQqZWouwLhn062486NmHaNd1RvrsSg7Izj1kbH6VRGiTN9y1Cj+/cy8/kKefD28ZmvolP92KPj9aLIBJPEGP40b2Xj+lVJdfnf7ny/So7zTLa1Hy3ZZvTFZo2k4BBqtALT6ldydZnP40iXlynSWQZ96qvJDEMyTID6A5P6VVl1JF4iQt7ngUnKKCzZsNeTOMP83+9zTkusdYYz74rmnvLmT/loV+nFM8yY9ZmP/Aqn2y7D9mdra3cbOA8QH0zXRWq20qgrJz7nIryhZrhDkSPn2arkGt6jbNlLg/RgDR7YXs2ev29kWPGHT8xXQ6askAVRuZB2Y5A+hrxuw8e6lbMPNjhlX6bTXY6V8StMmGLwSW7+67gfxFJ1LhyWPV1FxHD5yxtJCvLFPvLUMtjpWrQzS3FtDfxTA7t+CN394+49ePrWZ4c8b6VPKqWWpW8jf8APNmxn8DWj4i8G2PiSzl1DRXex1QLuKxMUEh9CB/Op5ujGlfY4Wz06Gz14aUhdGRy4SQc7evXvXumlWy2el20CgjagJB6gnk/qa+WpNX1C0vHsNXkm82B8JK7fvrdu2Ceo9q9l+H3xKttXhj0nVJUTUIxtSUcJMo7+x9aznDsaX11PTqKKKzKCiiigAooooAKKKKAErG8Ta3/AMI54du9W+z/AGj7OFPlb9u7LBeuDjr6VtVw/wAR5LqbQfsloqMxV7iaORGZXijwCvy853vGeP7p545cVd2E3ZHi+kXeo6Fpms2bPd2Vxf2DXURHlhfLTzELNvGVOdwBU5OeOcV5Z9+bjoK9M8W+IJtJ06+0ewvN11dzNbXziNWSW3RV8oKDkpgs/v3JrzML5f1rSTvJslKyserK76d8DYUuFdvt1281qixAbAp2vIxzyOi5xwSOcGvMrWNpnknxlIhvb88CvT/h741stI0BtP1GW7E6yObUQuTw+w7ccADchGd2cSEbTnI43xbqs974gvftFw02yVkH70yLwcfKSAdvpx0rWCbSvsRJ2ehz8khdiabmh3DnIGKRRlgK1uTYt28fG481ZCY60IuxQKeMkZpXHYTFIzKoyxxUsEE97IY7WMyED526BR6k9qtC0tbM7ndLqYdWPESn/wBmpb7D2KEcM8670QrF/fbgfnUi28Uf8PmN/ebhfwFTTagGbJJdv7zDgfRarvdM54HP99uv4CiyQtyzlFG52+m7oPoKhkvELfIC3uahMZkIxvY+pp5jjgTfNIqD0HJNJsLCb2Y5NSorjBysef4m/pVP+0t7CKzhwx/jf5j+A7Vr2dmID5sx82Xr83OKjmvsVa25PBaAjc/mSe5+UfnTbrVbexGwMm8dI4EyfxNVr7V0jJRDvcdh0FYu6a6kPlJyfvFRgVMpjUSe71y/uRhQIU+uTWWyyP8ANJIzH3Oa1I9OSMb7mQAegNMkvbK3JEMAZv7zc1m33KM9baSTiOJm+gqVbF1XMgVP99sUyXUbmbgNsX0Xiq5DsfmYk+9TcotmCFfvTQj86aYrb/nun61AIvaneU3pRcCaNERt0VyA3s2KuR30wADbXx1OKzTEfak8th2x9Kam0KyOgXWZ7U99v8JRuRUj+K5biEw3dskydmB2tXOB5FHqPQ0oZG/2T+lV7Ri5UbCX9s7AAvH6b/8AGtG3uyvdZF7g81zDKRjP506ORo23I2DWsar6kuB32n3Mcr4UmMnsTwa6FdM+1RlHQZxwxGK84stUQMu5tj569q9J8Oa7DLEkczKW9Sa059Loz5O5j6r4Tu7MPd2aF88yRj/lp9PRqwknVlUg5B6Hp07f/Wr3jTZrVows0aywMMMvrXA+L/A5fxU8eh5l+0wG6MGMGUAE709W4KkfT1qFPUbi7Hm1x/r3+uaiG6pph83PX1Hf3pgHFbkREDU7ANIcCjGaRQyYfuX+lOCZAJPGBSSf6tx/smpYhmJD/sj+VVEljNij3oKexqbFFaCsVwhp2w96mpuDnmgLEZQimkH0qfFNIzQKxDikxUxRfTFNKigRDsGc0FAakK0mKoBgTbS0uDRii4CUUuPrRii4BRRRTuIKXPGMUlFMBSyEYowmOKbt5pQtTqMXytx60u3Z0oBIFLkmqSEHJo5FOVsdqcXB7VQhuTSbsU7I9KbkUxELD9+wHQ80NH8pol4kU+oo3GsHu0WgTnApxOCD6cVGMg5p2cikmNmhZ/vbW9iHXyvMH1Vgf5bqp96uaLg6tBE5wkxMJz6OCv8AWqhVkJVuGHBqo7tCexo6Xa6NPHI+qaxJZMpwkaWhmLD1zuAFaixeDUY3I1rUWlQfNtsVHmf8BL1zG0E8jNG0f3RQ1NvR/ggXLbVHRi78ERCWNU12SF/+WflwqF5yCpySMGon1Twh5aINK1uRo87HN1ChAPY4T8awdo9KjYg8KKXJP+b8v8h80ex0Z8SeGlunmTwzevJID5gfUQFfPByBH3qI+JNCSEwp4QRo924CXUZGwfbAGK5/AUcCmnntR7N92HOux0LeL7ISJInhHTRIgwrvcTsfx+cZ/Gk/4TMoZPK8L6Ggk4YGOZg31BkxXPGkpezf8z+8OZdkb58bXexUXQ9ARVJ2j7Du2/TcxoPjvWjIXS10aNzwWXS4c+nUrWEkTOcCrEMIdtsY8x+5B4X6t/hWcuVdW36stXfQ2I/GfiZwVS4s4U+8wj063XHv9z+daX9s+INSsDHqGsNFYSDDMyLGHHooRQzfhge9YkZit8bUSaZf4mX5E/3V9fc1IsdxezFmLvIepJyay1ZWxcW9s7JQmn2xLj/lvOAW/wCAr91f1PvUANxeS/8ALSR269z+NW4tNhhG65kA/wBhae2pRwr5VrHj2Qcmi4h8OlJEN13Lt/2EPP51I2o21mu22jVfc9apmG7n+eeQQRn1PJpC1pYjITc/96T/AApDHtPfXpyoIX+83SoZBaW/M8zSv/dSqlxqjz/LvYj0X5RVdYJJTnGB7f40wLg1co2y0t44fcDc1WIZLiX/AFrgZ/vfM35VUCW9mm+aVI1+vJqrJ4pitvlsbUMf78h/pUuaQ1Fs6qC0ZhzGzf8AXVuP++RUzz2tmn+k30UI/urha86utf1O7yJLyQKf4Y/lX9KzyzEknk+pNQ5spQPQ5vFGhQtjfPOR3AOKzbvxtDtK2emoCf4pjn9K43JNAqeZlcqLVxfXF3IWmkwCeijAoM6quI1X/eIqoXVR6mmFnf2HpUuQ7EzyqT8zZNRmYZ+VR+NNEdOEXtU3YxvnP2wKTzn9alEftR5Y9KNQIxM9KJz3FOMY9KaYvei4DhMpPpUwKnkc1UMZFNBKnjimpAaaEoQwOPcGuh0zxpr+j7TZ6ncoF7b9w/I1yKXBH3qsq+9eKpNMlo6XxD4nuPEtwl1eJD9oVdpkijCFvrjrVDTrp7e5SWGR45UcNG6HBUjoRWUr4PpU8bmNt6N71VwPqv4ceOV8XaSba9ljXWrUYuI1+XzF7SqPQ9DjofTIru6+O/DniG80PWbXV7FgLi2bO1hkOp4ZT9QT/SvrjTtRtdW0+G+sZhNbTrujlHRh61nJWGmXaKKKkYUUUUAFFFFACV4/8Q7tbrxH9iLXbpC0NskSn/WSO3muFx1+UxD24r1yWRIYy7nCjqcV4h4svZLnxBBNC6C8tby6uN80O1DsO1AGOFb5EjP0UmqhvciXY838X6H/AGRoWhTXUpOpX8T3c6HsrN8n44XmuR06yn1TVbextlDTXEqxRhiANxOBknoPevTfiVos9pqN5azSRieNo47WJYlHmQhN2VOcjlmHHUqRXKeDtDlu9U1SUgRNpunXN4/mJuA2IeCPqce1PoMxLm3ubDVrqzuGVXtJWjcIwYblOOGHWqk8jSyM7HLMd2aliiOwRj70hyaiuQouHRPuqdtdEVyx1Mm7vQiFWLZd0oPYc1AFNWYXCkRh0Ut1d+iinKSQ0i40ipjPJJwAK14NFKKJtVdoE6rbJ/rW+v8AdH1/Ksf+2ItOBXS1zcdGvZV+f/gC9EHv1+nSo9Mmurt2hZmZGYvJIf5k1CkmynF2Nq91RPJ+zWyLFAvSKPhfqT/Efc1ktI8p55qa5a1t/wCP8T1NVYZZLlvkzHF6jqaty6EpEoiAbDfe/uirAhCjc22NfVqryXtvZrtjXL+g5/WsqW5ub6Tb8zE9FWoc7eo1E0bjVI48pbqW/wBs8VSht7nUZsjn1Y9BU0Wl+VH517J5Sf3f4jVltTSKJYbJNg9SOn/16h6/ENeRcgitdKQbnBkbuep+lU7i+nvHMcKlUz0HU/WoYo2ndgOWPLO3U1M93DZjyoV8yT2pOXYaWo+KxihTzLlwfxwBSS6jHHFiBQFH8RGB+AqjLI7jzbl8+i9hVGSRp39uw9KzbKsST3ck7k5Jz371GsJb3qeGDIOPzq3HEqCkMqx2xIqwtuuMkVKeOg4pGYnvj2FADDGoo2qKcuDyeKG2Ae9ADNinvS+UDQKeoxTAgaGomgq1+OKQnP3h+NAFIF4/THp2pwAkHy9e4NWWjB6VBJER8w4PtRewDccZ6461Ztbqa2kDwSFSO1V1bceeG/nSjg4q0xM7zSPiNfWZVJ7eOVe5UlTXqvw+8S6d4p8R23lxzG5tI5JE85c+WrDa21vQ5H5CvnJSR/KvbfhZGvhzwxda/Kn+makTBaL/ANM1PzN9M5/75HrVPZiRyvxA8PNoWvXDIP3Mkr9vuncTj9c/nXK9hzXrHjG0/tXSpNw+fh1J/vDp/UfjXka+ncVrTndGLjZj8A9aDxijHrS4HtWoDZMGNh7UQt+5j/3RSvjYfpUUXEMX+4KqO4MsbsUbqjzSZNWQS7qUtUOTRmgCXNJmo8+lGaYMcTSZpKKBC0lFFABR3pRSUAJijFLQKAEx7UmKfSUANxRin9aMVSYhlLincdaKdxDaO1O20baYCUooAx1papCExRjjtS4ooERTL90+9NxUko/d/iP51GKxnuWtg9uDSgkDA4HpRijFIY6N2jkV0JDKdw+tX9VUDVLlkGEkfzV+jDcP/Qqz8Veu28yO1k7mBVJ91JX+SinF++gfwlTFLiikbe/AGB61uZtkbEscCkxtFW4rSadT5MTy46+Wpb+VVJFKsVYEMOCD2ptWEmMJpp6UE5NJwBknis5yUVdlpNvQTGaVcBtuCzHoB1oUPKcLwo7mrUIWHhOp7965JVXLbRG0YJbj4rQYzdMQP+eUZ6/U1cTfKBFBGI4x/Cn9TUccWfmkO0enc1aWd9uyCPA9TUDJY7SG3XdcP+ANPGoMR5VnEFHqKrGJFO+5lyf7oprah5Q2wKqD16mgC2bV2G+8m2j0zTGv7e1XbbqB745NZjyzTHczH6mmnyohvc/ixxRYCw99czsdmQT371F9m53TSYPv1qlNrCICsQ3fT5RWdJf3E3V9o9BUuokUotm3Le2dn7t6VnXGtXEvEX7tazO+c8+tOC1m5tlqKQjsztuc7j6mkGDUoiAGXNNJHYVBQnSkzSE5ox60AGc01nzwtKTngU5I/apbAYqZqUR08JingZHFIBgSl2j2pcGnBKAEwPUflRtFP8uk207gN2g00pUuzNJgg460gISlRNED0q2QOlMK0wKLJtpUdkPBqyy56iq7xleaQE6SCQY71MpwBis9WKnIq3HIDz+dXFisX7afyZDkfKa9y+B/iVY7m78OXM7Ym/0iyTA2ggHzFB65xtOOnyt+Pg+Mit/w5rNzo+p2Wp2rkXFnKrjkgMO6nHYjIPsapq5J9l0VVs7qC+s4Ly3ffDPGskb4I3KRkHn2NWqyLCiiigBDS1DJKEHbHvT423xhuOfSlcCO4RJLeRJGxGV+Y5x8vf8ASuU142ra7Z6fqBj/ALOkXzER2wBJEwlPy4xt2Jjj1YHqa6bUBI+nzrE+x9h2tu24P1yMV5pPZald6LdyWsSSypE00UkO2aSOaOKQxhl+Zjn7m1g3DbQBTTE1c0vEum+HfEckN6wnuorUNvW0jKjGVBdpOG4VdvynOG6EV5r8Vf7A0a3tbfwvcop1SMi8WGQOPIQrtU5+YZcev8JzXp2m2uq2cMeoeH4VudNv4UnjSWQZCsMjO7HY/wCNc14ltPD2ub4dT8PC11FWKu0Abep/4DjcK0hy3syZqS1R4ZZKsUcl9J91Puj3rJYPJMcIWdz0AzXpF54LNyv2fTGkmtovmZzFJGE93ZlAGPrXIard6dpcJstKm+0XB4mvFG1QP7sfcj3P4V0TkjKK1Ma8u5ZBHE6KpiXaMLg/jVNmZsAnNJyxq7DBHCglufqqA8muf4jbYWysPO/eTEpCPzNWbnU0ii+z2qhUHp0/+vVK4vJLj5fuxjoopYkjgxJcKTnlYx3p8yWwWvuSQwGUfaLlysXqe/0pLjUCy+XbgxxfqahklmvJQACT0VV7VqRWcGlxia7Aec/dj9KLsLFS10l50Ms7iGEfxNVia8SyhEVkmwN/y0P3mqO41KWcguikD7qdh7+9V40ZmLt87k9SKV0loFr7jT59xIGmdm46k1L8ifKq06RhGmP4jxUTFnIRQNzd+wpXGPkumCC3gGCfvH1ojiWFSx5PcmnRQCEHox7tVe7m/gH41LHaxDPKZpOOnYVJDDnHFRwoTzWhGoVRSAVECipQCV4pFXd24pxOPlHAoAa2B8tMCszAAEsTgAd6u6fplzq1ytvbRlsnBOM4r0Cw0bTtAWWMqLnUo4WneJGG8IOrE/wj2H60BY4uw8KarfEbYfLzz+8zn/vkZP51uRfD2Rcfa7+OFj6lV/8AZif0q3deLktprYTjNnMfmhtG2hQDh8nrnoRVeA3qa2wexjP2XzGinI4OEYgjnLBuD+VFxkR8D2ZOE121z7uKY3gG8ZSbS+trj/cfP8j/AEqoIdTSG2t4pkjnZyTJnOOMAD8D+lbF/HrS6lbFIoJYvKgjdVJByI1BbPb1pagclqOialpbFbu2YKP4gMj/AD9azvpXfr4mksXFvLJ5+nwxKJGuR5m5uhOeoLHpg8D6VLd+GNK8RWoutIdLe4kyVj3bo5CPvbT7ZGaYjzoUMMirN9p9zp129tdxGKZOoP8ASq/agCrJH3HBFAbcCRw61aKhqrMvlybqYG94Q8PS+JtZS23+RaR/vLu5PSGMdT9T0A9a9bvJxPdW6WaC3sYI1t7WH/nnGBhfxPf61lWVgun+FLQaK8clm4W4ldBhrhu7P9ORj+HFSxSPcQy9crgg+38J/OtOZPRCs1uaMsrz6e0TAltp/SvK9VtxbapKAMK7Zr1GCcSScjl13/0auD8XW5jvyMbTnj+YqoaESOfzxilBFMB+XPal3e1dBmDdCKbEubeL/dpSfWm27gxIAeQKqO4mP2kUm2pCc80mKsRHgik71IR+dJjPNMBuKCKXFJg0AH4UtBzQDTEB60Ue3enKaAExxRjil7Uo5oENHpzSgU7FIenJoAQDtS7aXNAxQAm2l28UUueKAG4oApwopoQ3FGKd060cVSAb1pdtKBSgU7iGYxRinY5pcU7iIZf9W34U3b1qSYfuH+lNNZVNy47DcUEUuOaUmouOww8e9S+bugjU9ELD+v8AjVeWQIcDlqajZQgnuD/Si9rPzBdUTGXPTgVpr4ktNPjRbPQdPMoHMt3uuGJ+jHaP++axZJAuQvWolj7tyTWs7y0REfd1Z06/EPxYU8uHV5LOLtHZosQH4AVgzzyXM7zzO0ksjFndjksSepqHhRnoKjMju2IwfrWHPGn8O5oouW+xI0gXjOW9KVIGc75OPan29vsAaT7/AKd6uJFvxxx6Vi25O7NFZKyIUTcNqjAq1Db4wFXn1NWI4oYlzI4HoB1pJLwDiJAPc8mmK47yETmQ5PvTHuwvEYz71VeRmb5jk0xyqLvkcBfenay1AczvI3LUqoq84/E1TOoxoCdn+6O5/wAKz7i9muDhjtX+6tS6kUUotl+51OOPKx/vG9ewrKklkmffI5J+tNwcdMCjAFYyk2aKKQYpOvSlwSaeBj3apGIE59/SnlggwOTSFtg45Peoi3NAhWYnrTc5pOTS9OO9Aw78Up9O9KBtGT1oUEn3qWwBE7VOAAKVVpR7UgAClB54FXtM0i71e48q2jyP4nP3V+tdxZ+H9J0G2+03WLiZQfncgKD6DPGf1oC5xljoWp6hhrWzkKHo7Dap/E1tp4C1HarzzwRg9w2cfyrcuPEU0sFsbJGUNO0UyooG3ABA3ehz7VDa3utaremC+W3it5omgjAVQEY/dbAHXdjk+9O3QXmzNHgdmIA1KFm9ABn+dRy+BL8AmGeKUD8KmtYLxbS6Z1i8+KMxncvBYtgfj1/KmJc3+mRsiW37vGDIgyT70rMq6MO70PUbDPnWsmB3X5hWaeAfWvS59cVNVltFcPEu1MTL1YgcDHPX1qK/0LTNXmaCMx2+oAZKKc5/xoegbnnO0GmkY71oanpN1pVwY7hCBn5XHRqpYDE0CIWXNRulTsNppjDimBRdNpoR9p9qssgK81UIwcUgNGJs1btX2TEdjWZA/wAv0q7G2HU1qndEn1d8KdSN/wCAbSN3keSzd7Zmk54B3Lj2CMo/Cu6r59+G3xBtvC9nLp19aXc8NwVmiNsina2NrbtzDj5V/KvcNO1RdRe7jFpcwSWsvkus6AZOAcqQSCMEd6zaGuxpUUUUhlOSNpW2jpViKIRRhBTwABxS0kgG5AGTwK891vxZe6FYi6htYYrS1Xz5oEUDzU3kHZx8uc9eecdOc9/I6RoWdgqKMkk4AFeV+LfGti1vd6LY6Hb3Frdp5TzzzC3jkJ/ugAs/14o5kmmyJN20epw2m+LdavfFdhFDciXQtsWjW0kAkjhQyDCnYdg83axUsFwOSBgCvSvCEnl+FJJtZura7e3sopJZp5h5rHLsXkdvmVdw8sMzY/dMwwK4LTNPh0fw4JL1Ve20+SSfzB82ZpNqhUz95uAufevPPEsw1BbcXM586IFVRedibmby1PoC7EsfX2rZw924ub3rFrxf8Rb/AMQkWSXc50+M9GODL9R6fXmuFKtJJhU+8eAKsNJDAuyEB5O8h7ey/wCNRpMYQxHMhHXHSpKRYEcen/NLtknx8qDkJ7mq22a8lLcux5Y+lOtLZ7qbn7i8u3oKuvvMJRP9Gs8/i9PcCofKgwqASzevUD6U6S1kUb5m+c/wjk/j/hS+ZFBxCmGP8R6//Wps7XKMYWRo26srcH8aQyeC6e2IWML5gHGP4ajcvIcu+9s9TTYoxGOvJpxkVeMZNK4wSL+J6VpwPljGTSbHc5kbA9KeAqcKKAIvKdm3yn8KnUjPHFMJLU4DApADttXNZpzLLn1qzdSYQL3NQQLkk0gLlvGOfQVPjJxSIuFAqWNDnNACnMa44Oan03T59SvEt4VJLdT6VXb5n5r0PwtZHRtBm1VoC9wRiKPuzHoP1/U0AXkSz8MxR6bAwjunjZprgY/dqOuM9TWJaanJF4hs44oGmsJ1ZRdoxLzxuNsrbvQKeV7cdKp68Qo+aG6ltb4kzSmP95HJjlT6Fe3qM+vF3w5anR4XiZhcRswYpu2/RlzwD+NFmNPXUcfDz6beGKdUm8qTakoTjcBtPH8JO2ukVVmsopzguo8l/wD2X9Mj/gNR6w4hks7+OY5dFSQ49OMN27A496gs9Us57l7S32iWX93tQnZvJ+T6fMPpgmi2or6FC4t8XEiLnCvuStS9m8uOONFxLMi5P91Nqg/n0/OsSGXV5neRrSOC08475XceYuPvfL19uaS+1C4g1ad47CSaI/eCNuKEKvA9cAjpT5WlqhXuXbTS0liEUkKPnjHqTUdxpk9rd27aVJJ5EIKfZo8YfksW9stznsPpV/TblGgkmLOoDGJcr1YD5seuB+RIqO7vZXVkiQwW6j5lzlnPv6/54pJW3G/IJobDxTZrp93dwy6inyxXMQPzNz8oJALDjG7ABwa84vdOuNMv5rO6j2TRMQw7fUV209lqCfZ7jTpIlm3q1wsm1UK+rOeQoz60niiK38S6KdYsysl1Z4SYxjAlTs49s5p3uhWscCfl4FQSqCM1MSCtMYUhne/DDXCRPoUz8gGa1z6/xr/X8DXW3lv5LebDhB0xjge30rxewvptJ1S3v7c4kgkDj3x1H49K923w3tvHcwcwXEYkT/dYZqdnoXujDhn2K0jgJ5c20j0DD+Vcl4kvHutSO7adirjA68V3DWLhiGjDp/DkVzPinS1gkW7IAZ1C7R2xW0JXMpo4/oxX0JpNwJp8mDM4/wA9KZxjjH4V1R2Mhrng1oX0nm2ds+1Bg7SUQLnAwOlZ5yOlWZJi1oiMc7juGD05NaU5pJpkTi200RDNL0J6Uw5AzSg7lpoY8deKQ54oyfxoBxjNMQuARyeaYPlPNOAyetIRkkdqYCFs0gGaXHTFL0470CExSCnHjIpvOaBijFKKQdc0UxC596COKTANBOKBCgcDvRnHGKSlxuzQAA+1L9c0mKD1oAdmjODSDHrSZ657UAOJ/KjNNBpc57VSEOBp2aYOelKTTAdiigcgUZpiI5v9RJ/ummkcU+b/AFD/AO7Ufas6m5UdhfxqCWbZlV+9/Kkmn25RPvd6qk/jUIGIzYojfL4bIVhg4pp5oVdzDb0BqJ/Cy4blhQudw/AmlZ1Tr1PaoTLtwifMw4zUkNuXbfMMjsT1qZ1nLSI4wS1YxUedjnp6dhV6KMJwi8njPr9BUsVuWT5QFQdzV6BTHxbxkuf+WjdT9KhIpsiSy8td07bP9nvSNOiZCcCnzwOjYmb5upGcmq4jBbnpVJCuKvmTHC8D+dOeHZwTzRNeJbRjewQdgOprEu9SkuMoo2Ie2eTSlNRGotlyfUYYPlj/AHr+3QVlz3Ety+6RunQDoKiHSkP6Vg5uW5qopEkaeYSOpp7wrCo3Nlz29KVZ1jUbEUHHUVAzs7ZJyakYFs0qrnvx60KKcTj7x/AUCAYA9F/nTTJjheBTWbccn8qTaTQAhNJUgj9adhB2zSGRg8U5U/iNO3D0oJ4oAQncalRe9RouasKo+hqQCtLRdIl1i9SBMrGOXf8AuiqKxNJIsaDczEACvR7Owj0bRharPDBPKuXlmfYrNj7u7GB+NMPIbdzpounW0OnoqWsztD9oHzbnHVc9vx/CodMtpri2ePVyJreRw32dAB5bDoy+/wDOpNLt7qygdNUgdbO6wXiQcLj7si9t49uoJFW5IWsbgwu6MpAeKRfuyoejCnbqK/QZc6f9ltZEQAoMTRMBgNj5SfyaqgkJh+9tcdx/OtOPUo7eTy7llNvLw2TypPG4e/NY1/bTWt4qsh+znJWU/dZR1I9OeMGm1fVB5GzeKrwLcjj7a4kYejKvzD/vo1AUUKOMZpQs0mhxM1vtkjH2hTuyCCxVh+QU1Dp0qXs/+t2pGy+YzrgjnAUA9yabWok9Bbu1SG5kugQlxIz+QcZP90vj26D3+lYkV9c6VcLB9jWSF25Qcu5J+8G/ve1azyy3V5LcyDG47VLEKAB0AzUkNo7p9pT95Kp226xqWIkx94f7o5+uKVrseyLkrWWrK2m3DrK235Zcj73cfX+eK891fSZtJvWhccfwt6iuos7GOylFq0NzdSSkhY7Zd+yTOdzyfdz3wufqK0tVszrmjOXi2XcB2kEgnI+nrUNWZSd1Y80PPWmEdRUzoUkKNwRwR71Gw4piISKqzrzuFXCKhkUFDSArxNtf61oRHgA+tZg4NaVqDJMgAJ9quImepeDfCr+KLS7hjiZpY7YbWEuwj5j0PT8x+XWvYfhxpl7o2kXlhqd3Nc3bXJm3ShtypsRVDE9/l9e1eX+FvFkPw6+znUYN/wBqhPnIDh0G75cCvYNI8Q6H4x083Gj38bnILoVBdO3zIfUHGe/TnpVT091mcb7nU0VkXepf2fCZpYbjYZMFSAxGe4IPTg8deR0FaaSB0V0OVYZB9qyt1NLi7l3bcjdjOO9Z2s61p+gadJf6ncrBBGM5PVj6AdSfYVi+MPGmn+FYvnVZr9o8pH0wvqx9M9q+cvEviTW/GOtrJcSvNIx2wxIMKg9FHb6/nQ2lqw9DovHHxb1TxJcNY6OJLPTi2FGP3s3oW9P92rHhLwsLVZNV1eYiVRmWZ/mMYP8ACv8AtH17VS0Tw1aaJturuVXvAPvjlYs/3R/Ex7VHrfimV3EEeIoYeIolbcIz3ZuzP+g+tXBx+JkvTRbkvxU8RpBeWOj2aiO3toVmMY4+Zh8ufovP/Aq8quLp5WJ3HcfvN611XxLRx4xnnPKXEEMsTDoVMaj+YI/A1z2k6PNqcpKjbCp+Z26Vc25SJhGy1K8FsTE08h2RjoT3NOtbKXUJm8lQqL95z2FXL1rVbgo8pnSH5UjRcLVS4v7iZSgIii6eXHwv/wBeo0RaNma6s9KtfIh2yMeSAc7j6k1g3FzNdHzZW46Aen4UyOAuNznC+pqZSi8Kufem5XBRsRRQuTuPyj1NWGfk8lmPUnnNJ8z9acqKv1qChoVn9hUioq9sn1pQ2R0oANAAevWgHNG38aVcUAJQaM4pGSRkfykZyqlm2jOAOp+lAGfcPvlOOgqe2TKj3NVSD1rQtl+VBSAtgVKBt4HPfNRqMk1IeB+FAElnbNc3kMIXO9wPwr0vWVhjaz050LJZ25upFyNpPTn1/wD1VxXhGAT+I7VSDw2f5V1fiBnuNS1NY5YLkrsj+yFv3i8c7V6nIP8ACaLXY27I53w55k2t3FxDqCT2lxkTwbmjY46deAQcYIP9a7eTT3jVWV96/eUuo+f2Pof89K5nRNKisn8y3V4xKucO25F55G4hWB9mXt1ro7acQqshkzE3GYwcZ9m6UxdCvNdlLWa2t0EsrbWaAZUsm4K33ehG5Tnttqz4Z0VL9Z7m2naKM4bhVjuMc5jZl9P4W5zg9P4c6aaSPWy8ltHJHHEWS8CktKr/ACMBtwAQCeCDgj8a2dB0OVW0++tHmtbg78WzM0zyfw7/AJf4eOjY57Ctaa17mcnod3aeHNMlu0mgsLEwsz+aZo9wl43bzng8/wBayJdD0q+uJ50s47UFiomgyrOO+VBw3bj2rNl0O8jt5opr7VEt3lXzAwdTCo3YClsHac44zjAqtql8LS6EKXFxNesmc7yWROgBx646+1X7RRdmrk8jezMHxRplxZ3NnJ9qmaSOJjFcJtaOQbsspXdhT0+XtgVWsY7zUZMvbywRKxZ2kibnsPqfYVcl8hrIzrshijJbMcCeY7D+7uB5wPvHp+lZb6pNeasv+kk2LQr9mgJJEZ6tyff+I8msp23ZpHsjVvY5ZYHtV2QQsMESldzn1YA5/DHFUNB/sqw1dNPhv0ZHi8ie0aIqSHIG7cT83zHIx0FaEMUaKGK4OME+1c5qUOvz6ixsNLgCMP8AWCNJMKvcuR8v51ne+xdrM5nWdPOm6zeWTD/UyFR9KoV2fxGtwmuwXyjAu4FkP1wK40igXkQSDivWvhxff2h4VNrI2ZLKUovrsPzD/wBm/KvKHWu0+F10Y9U1CzzgSwiQD3VsfyakyonphcKNp6iuN8bTfu4eeBmutfk5PWuD8cSnzI0Ppx+lVT3Jnscc7l5GPTOP5U/+Hk1Gg2lue9Lnd+ddcdjFispIU5ximQkBMZ/ib+dSlW28k+2KihOA3s5qorUlkxX16U3ntS5yeaUg7Rt71qhCE9xQPvYpAuOtPx6jn3oAME8lsmkDE80YGeAaCBjocUxBkg8GjdkHjmk7cGgcGmAuDtPP4U3Bx608nmkyccCgQ0ZHWjrilOQPUUmc9aAHcg5Ao5pAxo680xC5wMUnQ0HFG75RQA4cCm96UHNIWzQApzSgUZ70UCDGOaXtTfwp2c1SAOlLmk7ds0oOKYCg+tOxTQcUuc81SJGTnEZHqQP1qtNNtUgfe/lUk0hYqOw5qnJ96spLUpPQjJphyalVGd1RFLMxwoAySaAgQF5OADjFZyaitSoq41UyMtwopCzSnZEML0z3NOCvdNk/LEtW02qNkS8f3u5rBtyNUkhkFptbBGW9K0YoELD/AJaP2A6Uy1tZJicfKg+8x6VrwRiCP9yNg/ilbqfpRawriLZhMNcuF9E/+tTpbgxIVhXyh/eblj+HamPOEBEIwxPLnkmqFzcxWq75Wy56L3NPzYegrnA3yPhT/E5qjc6kijbAdz/3z0FZ9xcyXcu+TgfwqO1VnfA96ylVe0TSMOrFlkZ2JJLMepNRkY7ZoBwMnqajc+lZFgX560gJNIBz71IFJHSmIMAcc05Ru6nApQoHWlz6CkMVsFcKPxqPYM8tTutGKLgA2CjdijFGKAEye9FHUUoFABigjJ+lKflGfWnAAnNIB0a1KF4yaRBxUhHFIDf8IWK3OqG4kGYoF3c+ta2rx3N3eRrfCSAB/NjifgSJ7evbkUvhq3Mfhu5kRWZ5mKAJ1I4H+NW9LF9HLJA2nOtuu3Ec6uy88kgN90+4xTSEXra+e3jEcLiNDwyAjDfVTxUq6naTRJp93DFCGfMM8Tj5GPUbCeh9ARUp05JObZRBIeqSrlD9G7fj+dZd1aX9xfRRbY44FjLNvMa5IxgZqldbAyWDw3d3N2sFtNbXt8ZQPLzs8lfVlPIHTnmvQtK8IWFx9vs9UP2qXcJGickQhgM5VRzz3554rE8MzXOmab/aF7bQ79mImSUK7gZ2r5mMHH8POMEg0al44vZLyOTRjZeeyDdB5is7HbyFAPXJP5VurJWS1MXdu/Q3F0TR59MhmFnbxsqFFmjZkCLzuzyRgDPUVxmotEdXt7awF19m8wljKVRiwz8zbfvDHTp1rqdIt/EMcyzSTvNGw+ayuSkojJ/u5x0yRzj+tZV/pd9p0iXd1FHEnKiQqU3AK2wDLEKAOOPzpzdwglZq5zltaBLnZeRQW0mcJFjfM69m2sTtHu35Glv9QdnNvZuY7RflAXALe5IA/wA9qcsAtY3k8y2M80m1WlnUFYe7Z6tz8v51LHpsDxyOLmGJE6sZN6fToOfbmsJLoare5yus2tzcxpGjzTys21Y8sxLfwgCtjwzbQ6SsUbTMZ7jMUsKsrLG3Xkjqf5VekhtpIHS0vNpIwWRWWRx6dOnsPzrKsvIsIvIhY2oilVvmtzEcZ5HzEs1TbQbfUwvFNh9i1iTA+WT5hisQg7eBXc+PrcBreYdTlc+tcR24zUIqW5XK460xwMVKwxnNNwCKYjNIwxrZ0C48i9VwgeRf9WSeFbs2O+PSsmVf3zAV0Hg7Tn1XxLZWCEK08qxhm6AscZP501oJ7Hr8XwVuPFNpZatca5LbNcWscjiWP7Q7ucnP3lCrt2kDk/MR252tH+CH9grNdWHia5TUhg28qwhI1weQy5LHPThhj36V66kaRxqiKFRRhVUYAHpUlK4zmNIv9YtdVk0TUrW7uzFGkiaqsSpDKDwQRu+Vge2ST1xjGekX5lBKkex7U+igDyf4neDNV8Ra7ZzacqFDBscsTwQT2HtTfDHwrOmW5aQqbmRcPM4wfoB2Fes0VnOHPo3oK1zxfxT4DnikaRJ5InkGN6nIYd8elczpfw+t4r37TrDXU9lH8wgt4huk/wBktu4FfRM1vFcx+XMgdfQ0kdtDEhRI0VCMEBev1pQjOMtHoLltsfN+v6Np+q6fHElvPbzWjuLWO8cYKE52Fx/D6Z+6fXOa841C+u7N5LMQvZlBsaPGCPWvrTWfBdhqW6SKOOKUnOCPlP5Vwus/DRb50judNE6x/dK7uB6bl/lTniJp2lH7hctj50tzC8UwmaRSE/dhF6t/tHsKjVQAP4jXst/8Ho1R3gsNQiAGTtbcB+Yrk5vh7eoXEQlyvZ4qFVix8xxOx3OXOPYU8IAK2rnwtqVvJsePn3UioU8NarKcR2+7nHFXzod0ZoIoJHbrWw/hHXUXcbJyPrVd/D2rJnNlJx1o5kO6M8HHajzCf4cVcOian/z5y06LQNXkfalhMT9Kd0BSzkUuQetdBD4D8STKCNOkA96vW3wu8UXPKadMVB5KqTii6A5DOeg5rqvDenXUazPEGE80RjKlf4T2zXX+H/gzrEs4e6iMIBGWl+XFez+HfA2maDAuY1uJ+7uMgfhWck5adBHyZeeENUsT++ES+++qkcbRN5bYLLwSDkV9W/EPwzYXvhye6S1iSWBc/KuMj8K+W7kqt5JtGBu6VSvezAVF61LIvyjimRng1NnenvVjNnwW6R+IrcvxngfmK6HxIha41lFeGJy0ZRwvzDA5JwM//qrjNKkMOowsDghxzXf6wkUmpLM1tczC+hXLxuAF44B4PfdQlqKWxzvhK8Nw0kE1+b5o+7xn5R7M3zV05CLcOYQquw9zn/e9vrmuV02zisr1BbWeos+CruxAjVfc7OfpXQgJGv8AFtbH8XzN7n/Clqh3uRxJPPf29lIp8uYjEkMnloW/3cHJ7ds/3a67QZblbOZZJriKO7QlpI2GVY/NkY+b/Z68Amubi0/7ff2pXIkikWTcGxtA7n2rannOmzGKPY0bsWWMON657be4+lLncdUHKnuaMWv+J7OeeQ3COkq4wQjKvpxgdq43WEjudbsbiR5laaJJFhhJGT05I7YHrnsM5rZurqS4QId0SPwXcYP/AAEdSaqyBDcSStNbxtH8kQOQVj6bd+3j14NNTvuNxLN1dAafNNcRxInlHbJc7dvTGPm5/KsZJrD7fA7gmaK3WHFuSkfTdz5mdyndwwH40X4luSENvFe2jk8JOgeYjoB8w6fSmWuhXLWQkmtmaaPOz91g+VnOw4zyuT+voKethGkLm3wogaO3Y/313KPoecfkKw9Vtbm71i1DNPctF1WKdfl6dUJ3fpWlEEjTy5V2nHDOu0kf4jvWDPeLqOuywMiTwW6eUkn3XR/UN1x0+XpSGTfEDDWWiN/F9nA569BXD7GK57V2Hj6ZWvrG1jO/yLdVOPw/+vXIs21CNuPrSWwiFwNta/gu7Fp4vtCxws26Fj/vDA/XFZLdAKhLPDIJozteMhlPoRzQxp2Z7q7nftU5WuS8aadM+lW2qZHkm7ktfxCq3+NbdjqsGoaLDqKMqo6b2Pow6j8DW3oulQ+O9Hj02SOSHTrR5HeSPrLK31HYce1VSQqmh4gnQN+NPUnPSvZYfg0bdglzD9qVgCHiuCjJ7EdD9avN8H9MVf8Aj1uM/wDXVq7E1bc57+R4aPm5b9KijH3x/t8flXs9z8Ibc8wR3Sn3lz/7LXO6n8KL6ASSI1xDboN+QNxPbHHOar0FzI8+7dQaUYGcV2dp8JdbvYDNFqJRNxH72NlP5Y6VN/zFfWdQk9+7bQABERAFlE5Qei/SS4IiXXoJRUAEpTfpNXSkBlBEQXqTXgRCR+lFDBCa9NCL9BZISA6/c+d/z9xzZ+4958Od+86sb8/svWfv53n2Wh/etXk777NmFKoeuh2W/MIQr86jOpz1XaUPLBBYXsR96KgGOxp4WIQHRIFXHk3rxhzjAX8dTkBdyOauaOmNrzpKs60ItMHVkdEc9GHgER4wMw7typkOwwOSI8EXAzdaW+azBTOrgqyexVzQo+kLD19WBZEGBrTqytOvGjG4y5sAR6vJ3ryeVdLZjzenRHVY0PMqGJVzkY7ljUFZxZIeUWG2oV1ZS2494jLU0oVX3lVNQQJHj/7qjN1ErKJ03mPYczD2vAt4wIuXY9L7gItcYMDeBxQ4VhRXCrtuICy2igzAhH3sn/JUfYK7WcqjzSJ6hOMpB1qmAg6x6vMpwQO60id19HMuLsv8O8ujxjZNQNEfYY6nHoeaevI5PNdvuK/+cVfSXOD5CYeD1kdAdusXUdNfNqI+evOBGd0y792w11qcEP+EDVrKq/O4C3G0UWQVcRF5RJmOgv2zpXkWPnYfviwzMxTgAR1RUns+y3hAldLpYLWlVSRdz/XwzSGHQc8l5KGkQjBTa9ZuMEpVKoP88knfyLxCLFjZ7bCQjk/1vjZ0LyvQFkxa/PbRggHLHzLELiQPrXTnGtPUES58JN6MB7QZt8NITQvdWp1EsYByPbOl+VeCHzODd5deoyGOodDivSs+2DaEtLtSwua2a9HbPcwoAc4w0KS6XlM/mIoYpv7cSvLotoLko2WqEL6FqnjrQF9a46nxYYEYAua1kEgPi+l4LN/UReN5I6FESjoHGbnHTn9NsZlZb2Gfs/iEeeIzZUJTtQHgcudfHFf8Emqy1my2/U6Ga0SJn5VG65TQL49hl/spmzFyH+FkzM83iWFMVylfPQaPZbKqhV5U5JFeGB4dXE6XYHWWXO5m5vY/4ik9nxtkqvgOJs+5gMAxRpuZ1vD4keQoyz8HJpoQn5HVxvDnCWhlbTkKd77roq+uc77+STI8MSUTU+QvLawG1+YKXMBdnVPwikqk+ne5NYLMgxwrxySnvwYqsWS3Acl/ZflOH9z6Hj0sF1rQ6M7/eNeI40Gsx8FiXeHnwYuZHOdxb+oZWqb5qdbJH6wW1dytKf0oU854UbvXIztaTwRCdsbWRXc8TCUXN2I52Ae3X9zRkRCJpArwS0oekLSrFo+WT5kINMpjYbXkIayJoWz5ajiZHJ5cCTDupS8dQvqM3pIu6lWDzH4OWAmlTjCKd5LLhP+hENqcgVij8IDoq+LvYoSS5VAPTeBhruo92prVIhpoQa2q8YmqkXUCZAJEi1Yu2dpmntbtcqUrrzkBnoB5sMQOfgUoy5gVTZsNXs3cQgE0Uye16NVGWl9Qao40KQN4qITcLIR9lKk7o75R+SLSmWQWctirC7AdJ9B15937UUhEXyK9EirXDnREq8jX5S4Ng9xBNtsvxvcWGfYhez4XHHV1dS/IMB2J0de88nLcmahYXYF38q5q6iSGx1TsyIxsFnXlWdPr7MWgbPnCN8rSW3Tip5TOVrMvqWeUWdRx2Q3acuHe6i75MV5u5CKLT068NjEF2yMWnPfhbWp1ASp7OdfkhOU6AUc/xv0F5aFeQli6s02S7FCvqdlK7Cc9tbDXTCQ0b5dzKbx3TX12z/1HRgoltz34nan7PoOlDFq3TRunz3mt7/6RzzTtWKkvLOv05g/D7vw+u96YTpIYqhNZ9aQ6+uZSkqfOVeEtZfk4/UVjXLe6OlsowALBmYlZMiuArvDvQXQwgmt7sn1zBZyKfNA7iMD1N4TWtf2G0O1dI7sJQRcf8bUy0R9n4Kc6s5JnxMQP8p5sw/UXNb29UhwfzlgJycm35hFVuTMobj3dvZrkn875lbhmKLn6fkh4qKMA2BUceO3YY1amWZvbmArebyvJqWYBy9ZNt06uZUzJrNk0L6oImFxl/Xnwcppr9rPv+1SzOu5f5ncAO/4PyjnDkFxTAoNNaSYqbCcktHCGHyh33k/pdFwoU0YdPvCSmCpfT1z5n1C9Xg6p+5aDDKkMVHNCQdu2pkTERBuAoLa7PHBrqfmi1aN4c48lKHoaoPpgBn28Gzx/b/83nY8C+LcTzDW8iO4xCRE3Q6FlfUk7iOcPbIisWP20pLuazJ4R3q3As5PBGTWRqszmwNlowEVeg0Ev5HhEjFds5dwWh95Fj1MGajR9kma/G9LLdxn6hFCsSluRgZk5W3baYHlP3sHy7rhApA65sgN9qtSte+jhTfnrFaeAMMGGh3E8hSL5yV99RgQBtHrK/4HPDNxE4vW6JC59MUULLEiTrv4/HthStlGvVpvPFWykC75QWWR+Wmj5dY4dHgDywQMuth0ZxF0k33TPmOMBP3SFjyvv8NQwcHcHyOABn4OsKk0iNJF7Pp+dl1UslW4xAGFm7coPAflxvKF6L17/YMml2dLmq0y40P+iv0OcOFZzJ5tel6iBSXxCHBOvLtpoMnQyt9ghMS1gpX1EuZ4H3JlflTivDOo/+tB98RAkkoF9dFyl7t7dYU/0u8+vdKw2xSj93VdWhcQXVAy5ZIZpH9jjDgT3VSrzlb4URavNyUQub2I6N6eaJB5FOW8FwP5wH9v+jHNLa4e95ks2u3rYoEZY1L7erfYp4escYci5Bx4wxT0Xpr81m69tk8j+UujZ+ysbBUBl/PDzKFeOpqSVo2K2YcJqEnkPIZx7RxNzoKeJ1NRe/mVmkYlgAWK/EnJt/UPajpv7Gy78Y56HivH8jvXk4qSdySi/1HBWMzuLx2Vc16T1B13pWfJwjvm9QbDVYdmVdvHbtrgpv9G3N/ebMBND8xweELRXGfsUo9n4mzBsb9f08qFdQ0duzZNeOEbJ4dUrTs3j29cE17JI19cxhmHczY2p4+vJ6yi50Q/XW5gcj6upntt6EeGaRK2+RYadQyEKPw+evRr4oK2+tJeu7z/+d6aiykyeKCcdqeCxmzEVrniH9tKPVOKWe0vkzMxC1CudxW+bLUnj1Fs/IyQnLWYuj7IqoJHXfvkjO6GtwX5TjVv5/j0fgmLXXyi50v8mWM5G7/NVRVCcfPmk2dAUC/RKVWgpWGN9crz51e6wIp7cPHM3flCC86M5eGjzlos72OcxHmAfcMqWYhbCMcExKq5c46Cvpb0h4mprWRYMJgjDaTl/0Pg70vF+paEVAd99opGYttCg840FD8jSDR4S6XcvgrVKoV54Nm1W8WnQu/v3QjKvzY3yuo6MSm7l6ooFlxJw5VQtbJ9DJPkwlSWYwWvkDn/dWAe/IyPrF+LE9jpxkarJP+yPQGueI9yhILodEG/TyYYO16S/XQhxoHLnTx3KnjJOYS7Z5Fy7y7EtuWw3qr4901A8INYrZlsYD7CB0Ky+/QY6T7tJlGA84Kx8qgLE7Gej86y0JDbg1cACWMA4BvsomxUPyH0JzoQm0gX3ltj0T696n5PsiW0F38YDGGuB/UxRmCuXG8IWSnTtNAVG3T28uCbMu4b2JaOFuytEvL5BJW/ihDDRWTAhK5hoRAyyBNFSjZ4oP9r5VaWdKcXiCcQDLFtLcYx+r1cM2E0+Ig5Ll0NeF4DJg4Sg61M6mC1oFOMFa1aSYIjCds9bLaGX0FZ94f5EyiQm7a9AXVI0REeqS4d8qMSZuhRB6s4WkqaLpT+8lBFYuui/GTgxMG64NrmTJUj+LuPsLijb5IY4GhwNP7M+drigzDlXRRvDsbyJRJi9f3cg3QmERuAY3oecy3Ao1IbhxC0tusb+vgImmdFLywb/OOfhVe0XpMEF2QHPEXhApQU/lvOwPj7iVvfWMI52q4PGz1i41U30qulmDmGhVWTtELifhdef0flmcGc84GqiD71dUkWGtIA0biHQ0w43YZ3d3JVtJTvdWF4wCoJ+lcDkcPvCGkdrcfEg3SYBmtTit+zQj7vOeI/1+k6KkwdcqTg1gcmxIooks9rgWSDqxQcUJKqQeU4NlADuypox9ZH2QW873gUNENxQRa/uo99s7oIzQPsY9LSp8M8DKvGEAYunW/SEUBBvyfJiqJrcHA79j33Pr67h2qEbPnuMIL8VeaMaHuHED9CWVA3v693pMEMy107weBQ4aoXZXCOkAtxVfMPprVAJNn/roEtKWJ4Na1v/+RyWNz/m7P/0eTRA+wrAzPsme2oyF0b01071EyF3/QIurg3U7wYcMmH5yIXDWyi/l2Y4cBn9Zb8DBTlYwJRgbokB8RQ3+wAfKlfFCmmZA4+2JZcMegOySroRFLO8eiUCnWejx2ABo070szapBKit+erRP0l1k459S6ugYnOHyGsp72teG3Rl5TyhTX36HID5n/eId46DZA9/pcbSaZv8Fo2UD2mu1LSi2JpSumD0Iu8DvVnAbp9oNlW0sop03pM3EFsXv6RaAaMz8nxX8QCanplU/ijLHk345Z0rCocpzfHf88GPzYq++blpTKCON+sSAsQdaeOYC6+i0m02T1Y774sHns+LkDYMb7TCiNEZTJWPd3Ar+6YbcRb5TNHzNpdQUMPWPbTUs+ilQQyh9P7LrxmbDW7RxlpPFu3rGrJGGYyI+BaXNDy+5lPHpcSyfind9axPhn1/1r/ZkrlOjwfYYfmfIdSQXruwvxiHoO3QJaExxCTMbdcETu2HfJFkrtkk5FFfZtENyLHDKAI/hxC3R72eqeos9tPRr/+uVn3G/+f801LtlFiT3aPzrIX2lmll+WdJ7zdKlYc9P6LLOWrQO2dVasdtTW1FpAeJoSEvGZdX4E2T3Evcw9Q4xQBI/U4HRduRT5hjS1paR3qZCVv0OLQ+9qHJTTOBcMu8hJKHeK9dNWaWOtAVD10tmqvAQiPdgyeS6APjYjjOJNXSuOtrrbgIBnaTOmMrhltj981H7UqsX1xCSjb16tOoM9/wFCoY6Yu1UQdk2Jv0H8bZCyzIlEu2uKyvdUm/SonFA97m5lP+cOeZ529Dgu75ZRo892q0hWwhjmG/pv6CAQ1TwPZsTtAvcF982Bpm23e69icG7Kj9J10vnJO1bfN4xGsW+iOY77bq7EGGuuiA4erlmDvIZ0ENKHFauEToRQYh3DG64r7pFoVIHImfz28tpI7Cj1M2YfRNmGv04gqqsZem+ZTcTB3l4mo0/4nmPm4v2LoILaU4fo/cQozlh01g1QpUdsHIULEMoCsCWL4jRDrwEERwxHI6TGvm3AvDcLVgqMJmzybskZGRUhczhOC7DadZtKGH5W5/TsuhhY4eIqf/+AF7y/re9Ow/OUsM3Kujd6Fmp0M8RJ+RWGLUgngEa3aqiAyJVSYwRmMrP07a5n5P3HtZvgQCtGG9LoEyrS7pCJSlAjS4Yi2rFPlF6liamzkHIbEeqGhkPRp3xb3amCzkJaf1nJ+Ghn4hRlEWtmsl16P0bHCQz57gB6wSzPDgTrayRru7Q9g4WuXSuvnTrLa+3mXKDYHAGQXqRmPFyA3v5zdO8UhSnAv0V77zOWmvHNJi6OYnpGr31RaU0FIQniL9WmadrzobkiWnm/YjaQE3ISk+Vh8R+9zO3WApo23U9sCbQHH23omJg4dg2prPaPe9u1JybNLW83TghbNKkyp99/yFi7uRvnnhj1thzordtFpszmUDYhFJmY7VV5DsPt7nHI/JfACECbbYpgMkYX2N7ew3xd2Wp9t7L2yH20z7j4LtX+lH7Bm8VIv3kP0wVLoshgd8T4oM8C06XoirH4phOf5V4flz1jPitJLnHgnDjuz9Cb1gDi3Wv6+dE1HQ+Ou8g12Nn03ZRt/5mj1dryO+lmIDQ8Qv4xVzX0iGi5HJS42eSphBEo3e+Cx7sSGx5ZlMn1n2TF6+UEyaVBRE8PU6RPd+Ftx/eLtCMJlF0yiZdGAg+l7IboBd6Xn5hpy9sNAm/LNEUVmm/SHIeDbkrZXz8p1Kl1tIy3nzX+x0cA3bllbRh066d0UIpCkWJ5X6GOtmzTgjnYPmidlyWnJ9L9ZwXJVCJjsaU6p0lVYKuBKBnrXgsdMHGWoKDv0ZNoa0M2vxnoHeVTFdV2Y7ixzjp4s+8y/zZSzzfIP6j0de9XiMBCB+XDOaH9DqVKgziJj06Ev9FmU/QmObsVs0M1eM/3DpYn4S3aGnBgPs7ewDpaG/SLRJdMxSQ9ltwrIDkv4c6Bu6kqncmTNJYmLoVf/3vz7/r/C0fHI4wcoxxhm1SuKlb+PseVr1KQ6ARkDG15EHa2ET4TH0Ellwh82SomCiI80f5d40Tg/1XoVhJi37p7ctqTwJVN6w39K9xXR0fEqLYuOYUNBG/swF/v7MgojGqiXSGtNdiD23kWlosWonDwDq7V0H7FWlMIr1UpZpnn9KKYFnWIx1oI7bKIIvZ/23ty1tgBLjDqzcrcj8h0ji5nrua8OsjugqsZrC5tgGqtv+mQ38CtpcBrB6wJxtYtMQPcJSG3DQK6vZ7BIyvMlePsjzvs8cZLYeiuh85lSNbAimMVd7nGGkGq21Vf0ozsgaSV3Nzbo8VR9AOSFFcjx+aAGU+cLeBl+4Z0zKv6GiIyMz+EBLxfz+garn8OOjV0SDX8VaOsb11BCuaaUepcqChT8H3kTFP0nKjZ5dWr2c9uSOft0abhv/HOnK9bR3fGj4E8CG/3uV52/HouoIb52692/Hvc78AdQax/DB6xWArtjSeMnMTMj4JklLVZFHQGNj4/dhWZFLwdUB9mmPvYEtuSlcZmH76UmvOKE/uz87RrDOzSE9vJxXAcBdimlbTbFIK4rqiHprjAf03DfLT/YxXZFko3j3hzvHpWFk1+p+hTia4/thQ6oi08H8Xrfo1RnY0qGIPrZZbD+PMz3s9NSpNHVV34jczRkw59ZHcOHsC07iHzxw3Ziotm3KGpb7+kG7paVpQohxZcM4VYXjE1euYI3hEISPr/vNq/KEQMOn9m8566B3DM9Ov/EEuhiytO82oe2WY45AlZsveR6OZf3SKXrXwvVBsrms186NqfUJQRgi4AreZckS0W3GbKz3jfoeo/GP9VrkYS6lJjm5i9hvOXO1Hg+2ZYLp+ckh3qT4x2IixCavYHqK9/p9KX49F7Dt1/8KQxSZFj8WcHxAy5cUSnEn+H+VkP9C13IAHrDElaMMUN2gUsEDOiiFjraWLgZLxhTvMyiyAHFo8Z/+5KCxtpyrjSWUMc//7lP9L+Sn3i6m/8ThsTVEqakMsHZkpRlroLUWzPlkXq7Y9wQPSJoWhR5GPOvsGvTwGeMdKkylIz8dCeCkrYjx8YdieRCU0BCdYTygWi2EGG2fxKqHhp7tTtgXs0eNh9D6GWj+fMgaaPOB3yNHL25boA1c6IDoQGrDE8NuSf5KOeUucvpXVerrEo7pDt4ZItnwgO3LCR+LpyjW2DmpeV5fMuABX3LJbi4WAM9/wkabbzGl1c+MtMaRX4/FhBXunOQMSxwtPpeiaDubnbzgGC0cbdMXWvPmG96hMrtkWrGK2DzMiS1WoXBxpW/TSSoQJxiqYQebvYMHJEhCWPp3eEgdcsnB/k4GSlNWGs2XsSKil6E476RK5HjRD+kyotGihhiDhrf19r9ospDF2mblVWnrijZIixKV11WJTVrTsLIrnrWLKhvVKaH6+Ci/9/bfT/r+dFNtW6Y7lfkF9j7Mvy/dmIMLdl2bMcQDkDIxen8npj9/Gewt53iiSV6gUlO8cUKC3EasamupkLXNFUvHijQjjljnIb7+1tRpuNF6zc9s+oLLLbB0gwkGyLqzN7Mxcwfr9+YkwwgNeywiix3epBob7Pum48yqbueLPOLtm0z0Y5eoOpRnPbCvrDsgIxJCzBFHrEzBqLKL0OlrWD6cHSRa0CpxfLzW/BwTB6ogGwAWOSkXOpy/U/n0kDG4ske+Pl0K7CBFuVXb30pUyalTbo0Ippa5lmRqja/5JPJkuL5V04PtdgH9JanGLPKvy8NZsoq1psAvOVKyFUtSHxUxKVUhbxH0D+QbjT/9Tvf9a8L3Nb7XBDW423j/BIi+/wCx0yENh8MGx9OD4lqJu3l047fipPX+gmWLhok3uIrASlaQyQrsk5JL0X2nYs5GGRIVG+y7+5PtLcJTbS3nO05zMdl2Qn/faQn2TsA9xZFqFjPH/ZWQoLuepnBPLeo6+h6CjFdr47Ucnr33q3QU+BSzp2adWt/nhkt9Mn3J4ZE7+JYbQDA/PWV563DIT6fLJ8OVdJbqoErtgN97P+CVMHBhxN/uJ4xw2DsYGOdWYFXXZeHC/urdOAUlmp1YxfwWsK1j8qA+qiPvhuCIiYDevs5lDU0qhH4d7Qa1P11eKfwPM6T/CtiawuUy/dnSfDnijKKChm9Y/l3NvF3PgufPBdT1SUk68iqy3BSRZxipho4wIPt6UNDwqTjBUUUb+Ky4PBozubUoj7aGov4UNjUk7jsP28pWE2Ep/evjxkSNn1VmR4cK8Vu7BwTEZdFmY43fDahqK2t898LRvCDfcfcwkwzoK7CFjlVXPWYNV4IN1Y6vhQ1QnpZcF0J9M4RItfAAMngsTVj5fDDZiGHzkWW7R4pkiRzRgUniOwaYeLeIeG+p/PSTF71FafNX32l0S4mpvhVT99g5XGXzZtb40qDvQMjvpupl3w0uowv6upmhKr/szieaEDaV3G/X/rIGuX/Gn/Kg/k3sPp8Wv0r75IENHB6V6bEeum2lhWb6IWlJXxNtmm8qPEBxo46HwdYHivRL5DhWqZhHuNGJ13iApvUxexJkabb92f/hWdb/V6hiv2kpBn2sDKn0SKmaoMNkGTcjPAA81RrAQ4RyKpfLkt3ecy2wX0usHShkRx5XF4O4g4RhvaKgguKy/m88w9/oT4JxDSd9lfmOjA+Q5jsimjSlc5+sNhUZdjCOhs4T0qu5WF7DupM4QFuMt0ZTmegAuWfvC06ZgbVAo5cq65+aS2eoTs23U6CtrezHEpWkid7KeIAFZRbi2juU5mXqb76n0r36r2un4In7J2njXqOqFTJlF6zS00UJvQ96jMdyUPD3nJ5vUcFa4r9kN6IPmgTJXG++z+09xxqLVX/KmhCWWiRvuKe39b6nLD3gtGjvF70jupjn+WHkkaPDpnQh0fecw6pdVH/3bjXDzmMHJaWCuSbM8+s18MlIsPnEOTYMfniBUr6Ie6M5YswfLwh0XU+3p3J/BzIiTS6kOXmVxL/NIqVTP17BVlsD1wy0h9h6sKFULw8Wk+FA6zcuxSbdbxyou10IbyVJbJXxLdDqihQOiP8PQfHfxS3X+Me03hQVIk8ZbkHoVqiicMzT2H5JPOBNVou8oo3MLuyw1/dGp/wK4UVLVWzlbdYa+LoWyMBS+X9zNbaGKzGPqiXJPahu2hU7URz3BpgdaDemxc6bFjDFXp3lUsW9T4GGxaDUuNiBog/O1je7q8mtVF67CLIjjlR6GDfX0TTL21mxmIDNuhcFN1PmUn0BjfYcbp4U0TTj2GGVwQIgQj+Zl9RXH4gmGKZzBh3JcAR+r7W6yFvRddLzOzO7fxVU1y8JPDeFxeEyWAclOdhHGqsXPw+VftaYV1ga7Q5xLJzHNA2nwFoTXPpDvlxUhc+hEFGVLlOPilQw0NjPaziVUJDtaBB7GTp8/TG8MTliq+GvJRANdAGoS8hAfGSUL2FoSLnDrFF0Opkmk8mywQTbLuQbEY3KYSMsN9RZYIyDiNV6vdz1/0OF/c9KC+zBUY9jTV+7HKAuz5NTv12mY5W9xHVJhywF0eorVBQjgr0NrZYmhDpf6EbqA5Mmu5r8ZgoHthZXOjZ7310thbbJrBBqbWTHs3v7KT6DagDQh6K6z7ImSDmSmrG7C1jlQ2GtJPMndmWDrnZZ1niAQVZuuOdFdAAkC/0BdeIHNeuswU1JAd8Ygqzhc62PdLT6gYGnJdYv126tMQeMx7ashaQ5nqhK/jZ8SZTgub56NQnkDPXcCEbCWqfjJMhTLwevf14yftgjqnfCA4Im9ZpSTrxBaRyv6lY9mFcSFZOH9iaWAwxk3MxGG5GU3RQjCY2gfWhlQE54CLXJLtEendnHkre39e71nxToNm8ESEWfsfjs33YRnLP93k+aPfTc4/tXoY3+6WOJfRwlmr9wq/zBYhtEv9N4IIFmjet2Pz0xAtjbD/ZNmC7j+6hM0TsAcFXQaVdX+4f+Wf+nSiHF//k3UEsHCD52S+NEnwAASqkAAFBLAwQUAAgACAAKvFVDAAAAAAAAAAAAAAAALwAAAGI1OWJiM2QxZWEwOTI2Y2QyNGY2MTM0NWNkNzU3Zjk3XEF1dG9fZ3LDvG4uSlBHvLt3UNPR9zYYRAEFRJQOAtKrSO9ERHqT3kGkd+mdqEjvHYOASO/SO0hLQJr0DkLoPdRA2ub7zru7f+y+M7s7v9/ezJnJzOfem/vcc85znpNMsAvYf4AnakqqSgC8ewAAHu4FwC4DFABEBASEBA+ICAkJHz4kekRCQUpCTExC+/QZGcVzOibG53QMDMxsLzmZWfhYGRi4xLn5XgmKiIgwcUrKSgjJvBQWEfrPJngPHz4kISahISWlEXrB8ELo//XA/gaQE+FF4qvg47EA7pHj4ZPjYQcATLhzPsD7HwPwPwfePfz7DwgIiR4+IsZNaHoCuIeHj3/vPv6DB/fv456G4p4D7pM/ePpCUJ7gmY41IYsnhdDnlAIi1jd1vZS6k2dswh+8vjx8REVNQ0vHzsHJxc0jIiomLiEppfBWUUlZRVVNT9/A0MjYxNTG1s7ewdHJ2dvH188/IDAo/GtEZFR0TGxqWnpGZlb2N/DPwqLiktKy8or6hsam5pbWtva+/oFBCHRo+M/U9Mzs3PzC4tLGJmxre2d3b/8Afn5xeXV9g7i9+w8uPAA+3v8+/m9xkeNw3bt/H/8+4X9w4d3z/88E8vsPXggSPJXXIbT2fMYi9JmI4k1KQV3vQ1Zh3TPKD16Tj6jYRDbY4f+B9j+Q/T8D9uX/E7L/A9j/iWsJQIKPh3MePjkACLi54/r56dH/yrjjNxQNwBiJ9l/FngttYPFH/a1zX1gpdLUkjvWNLJJbBJ48h6Chl2PUrc0rB+p4a4VOM/41dij5J8DDz9f4KOdntW+0/LaQs2zD3rEHvh82Hh5wbxrIDnrhW8pPUoRRbGxSWh4AeSSNu4q0eoLupmgp/GtUAsCCszNhIkzPoEuKpX/6c587gKO6GJ3v5hnWOAkLn13q6TBR4N3kRs06bn+4TpEGvdIj+W30ZI2/2arLmw5toXxVoYfY1Xztf2BYedUqjwU06PzpX2LtToUbVnQXEZbuWrp4wgmVAWmVi1jAvzdM2yb1IW8mxb0rzTCPtTEjysxdtSmHMWWRGHbUgU+nHkrhopZBOxr8hBXDER32eQIzYghDpBUkgpNZl8SBSH6Gz8chSRbU6gdAKQWf7sKLWi4sICLn52NwOFOREAguSovI/Zl/GwZCwjmxgGfKPExNylU5v6WTxgvFfweF+W7tbtrHYQHAKdB6DBABTuhm34vCfCABHn/NR2kylFnOXNUeP5EFnhZom52FAqXgEETKT4dcfbIqXVAED0p58iHM9CuoM75nVG/rgsxlK/hVp5XHeNZxzPHtfIoynFDVHbxaCuOpvSrPgmQ+BVXO8Znte+XDcCArjoIqLT/fvGuZyvZ9IgVlxgI+gS8cO9/V3gjwL6MX07EA08a8FzlMvA57jlvWxyl7+HpRbdC5UvWh/MLYfyxwyr8HbIMWUQNuKGcQZWFKesVgbg+4dVyR8cNd7BY0utD6ggulKIKIfRIAsM/iZZKSQh8eqrcacTJFv3DHAqot4kwiepKwAMbiP9DRBFSskKwLE1KLRe62JPctiCQcXmwvXejIMDVnLo5sj0c/dj7XqpH6K+TMjUeQ+b+O1v8/jPvhoEFHh7oPe9LG62eqQqV6Bmw9BvcvGUva3NQHnFOTS/kCiL6DIe0zpbnEMnH5J/itGM7SiwKOa6EM44H9WpTCIwJiZmDtORZAt+Muuv/SIhNfphq9oIwLDoxo9s27XTZC4PHzvp9pOsk1qwtW8r+rYfJdlxIHH7CA9DydMo3lzuxNLMA5UAl0bWNwUtLeFO69pvyCk55F6fcNn6aRSwlntcOBYbJz5uGDv34J5kDC27u5vD+8Ng8sNQ+G1gcNPcXmZ144SRdJZkT9+1yRAm/UHbJpaZk5MQZNSNwjQwX2FJtGqU5vYAFZbrsYsPQrLOBRe3wdl/GkjvLruHjdrTQR381mjZEk03l3ITeULIvATY37LyB8FtPEIh7HgVxfpIq7DCTCAqCVKn9WVcc4s2dm5Y6iLC4V8UoOz0G1cDrosYd9HGpQ4JqiFgtgYmSbY796+AqXpomzU9Ayiq95u0ymIdFZhqF/QGcJjkegKfYZdzK0SBcIXloaGSIWBVzUabvyt8c0Ab9NrFshD/KiTz7Gjl3Slo4w9k7oXNG1A6NgkNWnv9EfJi4qiV2KlW9EKvEuW0y9nO6+Zp8fuefLJddhMiQmRTP3i61A65EUwT/RsBNBTfDHZsPw/Xu45FV7yWyZOQfDLNQi9Kb7TWGXUzUgSvxb8LcQ1k0qBqdUsqq6JDQ4btCPiV15Mpl4KErlPRbQo46hgJdxgGYHgMfgmZ6zqIAozGcE4wUUCxjUwQKIIjullnA51hKNBUDyRUIijg78aNFFPRfjAsjrxp4lbixABufWHhctLOCruiUWkG8MOmMHQj5vkIZgASNFDpi1ZyjHnaRkL/0jzusvTLd2ZOg7q7MfVgq4hfxYwOkU7uAqMvSbArdwPSzAbRrlKEcGp8ECsj2B12tADE9iwC3Z4swRhH7kg2RzM/B6ENiXc53DcWjjCDr+glsr28m5SUmLGfG+BAvjKFOfdKMrUGrfHxg5jQInOnb3bZW1C73xgSKX7NLIgn1xQRFTdUkrh4koEZ9bdBb+6aKAsRbv+cqRvG/aCjwnngGeUU5c/oSfE+tb0FQXIkzlLwL8NeU2SUA8nzsF/+0/HI+4l39nf9RYa1emBAq0Dso/NZPAfCiw4QlFbFlV2eo4Xj92jmtlIkS8RY9IZ5thvlm0liY9dHTBlOrN/QAerYnKX/8AJijDsID5YmrnIJWem7/FuAA45lz5JfMqFuS5OeYMvFkAXhRiyI91gDMBUx5ID+eEd3FfQHEicK+1VpTjVnSwSSbrFEqTemX+sjLJqdoEhzsE3EQD17dwa8xJuoP5vcMCYL/nAjpC0AfJVhIYHtnvagY7OLJeMkWZq2+MNN+0gLlBZWVWA/V92ksiqx/Wn6svSpOh/H3ftqeHF87sV68oTzmgaKau1dusTELfNWPkplIVTUSNYe7ZuXSsWEASnoXSNxg973ei2mP7iRsOQ0zTBMhjFOYaYUvY8Kn/qmLqOd3ezq7itJ1cyaI8alC92FtlsyrIlW7AnSCgUr2sb5WxM1NW+rUeMi44R/jQKZDF5owtaaoaer+u9o4zRgB2aVZsomi/1+C4uTmhg3TOiy+Fl/L/OyGq5Q/Op/iN9+VQvft5eNhe/ow+J6R9LnsdLnR2NeMM3C56GmU1j3JmoFuZNYqTDeVU3nN+LV8rMt3Nvi8ccWEHxt+XYQsrFJ0zDsjS6sYf6vx8schGi6pwdS769lfnnbKUxEbF+5lYqliNqR0caY5RAHQU//tN91nsw0G99nbjma0zLjz3E0N2tmRADavpLEe7QyLhUnhUch7PTnHYPJ/SeZ3AGisi6UeN6fWpt5t2htFJxLHZdOFYpUQd5fFPXsFEKraQc3//Q8SjSr6jXUmO9O9XEpSlbhvLbfyaq9OD1raF/J4+ywSyr2UwvpNF1DaRr3KVfcuj1ekcdccavdY+2WL0R04ZAgRUvi87Xc93s3WPE0ys9mk3S6JJjTxoAzC3JiJd4hp/3ZZLZiwW0Nr7Jkh9DKU3qNLMRJr+nSNd17hMtdjx5z1ToUJcfYReVLptaL5ZIehKhQwFrazyYAF885SeJYgW/V19eMIhPupJJv5tbC3TJ75t15XVA3GPlcZWXHER0DmKLJ8068iNW94zrNDcjfW5hDqSF6FV75Xn+v/2wwIOUYr+L5guIA+sdsGDcRvXSXSpPrugu33W/LNy5SgZoNNN1eUCHAuQtZTB5cHYu232ztSXgiXXcSABBPuijNvZCWMWXdH6GTMwdYpzwAqvlHwPXD15nYIF3M3qa28cGkCXGlvh6KkoLEB+jBWR1p/sO3sMRXsnap+Ve52yzGb+RcVFbSp9KhXLu9+VhmnnFb8QuUJkiQEn5RhZ7qhbaNEu7Ci7jTosQPChLfDo9frMjA0kCJc2FXE62VjAtDSOhTYrGApQE3ARLQuWHnyfEC24I3CvmzwRb/kB9Z1uy0B+tO7HdsVOG3Q5DPOlbnrAEoQKDvCwyJl2awDBOUqp77byDzpJa39duQQSYqaLA3xbT43q3FBucCprTMmgXAsbiNXAaiCf3O7P7fUj2ZMSIFJU4NsmBNhxxliOBeCTAH+UG65DnzKtIp7iDhPmChKnmC7d4TUM7Xka5ywnnXVqsW8Vp7I+OvNYxo5zrWuKEP2L8zZ2iU55QJVw+N9Quh/BiSBquxD5bPMVEzCyCoct7BqIkdZUk32pHqFVHgphWgwxXvUlFQzLDEdxYSbgOoeVC0nFP3D0uyQFTEq3a8wlB653aYD2fCatYRlA+P5G48RNLS5sNsul4hqQ0KMtJE2/JlwpcO4YRMyOWxYwFaKN80crkJi92tsO5r7b9wd4eMVNmhVvVj0RQYjuhqKdpHLTcCvtZjFEfzBDcCCa0O0CC7B8k3TU8yzpNtEMI+Zbi/4GU2JiX4/ACWhqTxBcpLwIcfGTjGw0mMdiwBtVdl1/jAgvwgKK4j2OsAAKARTkGEivlvocODilkTJYuZiV8oWZamGYo7EmC2IqI+devaHD/ovWqZrej7Cca+zziaI2QaVH8Pv2vCxh+9WMRZX+gdA7LGDdgqerfnH1aVnHUfdmBiQNFvpy221nrpriyElBiTYLny3h9xWsoOoYaIiI8nW5f2b1e1iIMMmn6iHhviHbvOmdia36Z08+v+mV0T+35zCVHNpeDIcdzeGgjyV9E1I0MwfP0INnlfBP28TI/FXZbqd5voLyA1olbneb4pvBgOglSig6lAG0pz9dizJU2tVo9TxoIcUV93mDakSaxtmdPcar/tef3+E+UWfHCPAW/WZKe3LNt5+aH8NXv+PyJy4WlmA6Nctaob8HVVq0wTytjdl7dUc6HfRpdB0pWCIeh/IjcDhLGM2/Pu240wX1DXdFhyH7WtRPYwgv1N4jWpyYnu3d6ICWzUEilddN89pQzEO5P+GnN6DfNGvCcALQlAyhV6gKLlmOfSYQmt9BUOiX2mfrR60YNZ4tEHWjzcjSmsCU8TAmwx0YZ/qMywORzXX9DpSmc3xY24CIW/gbCsIn7/QtJrtaY+qJDrrVAF47x2GerZM2WKeeMFU8w0kCo7dy/I5Ey5OntmGfVP5UAE2LOQeJuSXe4US8RQnhnQGU3OxWoziy/0Y4CxJGn1aMigYuf006cO4LyO8/D121J8ECGquA16bNeeJnx382g2kkGfJZaAkPfsxGzMoxrSr1OE1dXnD6IZ/oIeBGV+1xASlXpgJOlGkGU1tIcFcWGg29uFfFPtaZf3BaTY9enEc5gpc3qv8kgMPyqtfxsm4/lK0itH+nDtjWUUG04MWwcpTQ1bvB4Q6RoczHYCNdUXkviYAFUAMPOIyT6Td03/wGxRzEVvgqZwB4+edQAk3KiWJ+V3qXoG2UdHCwPtVBUXLHkJghmyYlL4MjQeLYTH5dx3ZhgWnR4fxHB8lMlyAKK5xmt2AhxALsS0F2ASXkyFryfgG03ycs4Gr/Qr2Ocdgna8c31dxkFf+6w5ENuGa7BBIMNwDWi+x6CE1tqvsd3oQnwdEuBPRJ9MYtZCVasnEvcIQCjZExIscCVM62u35fKcX0gGdaqOGsxhBPhK3fnd1cqV2jojg4HBOoPoE+n5136mYG+5Or0lNDtE+GmI0SsIC+YNlaVCjiTcDQya9fTGBy0yCHwWqioac7xCNiz+dCYGd2mKa0eCnhEkoe9grZYgFY8kfPy9K47o/aMHO/jM0uakM7FzetJQd8aQeLhKSyIdG/b69bVGTKp/mExOS2gXMF/XVVzqVtDQwFFUH9qnaN2cpc/9BzRy6W3PhlogQDjTqKAIr/VtP0IyoCA2oDPzJHsZ0HUA5ZObv5+rj9dAeM9NwYzSU9PYwj0f1DAwgnxoAm1CAJjFDNZQFUiHoMx4TOXk/UxZiTGsP4qa23Ufmfqhb6stXHOhI6y6L5bjaeZRq6lBP0ucsRCcEN4hp6jXGBV11qKkIUvDDecWpO2hsJYLU1AglRWlI88/86M+zN+yDP+JbtzqEHCzATraojVxvajaQdMXlqiVjXOrta+DXlcz3TBHFLCY9ivqu41Flx4E8scBHbVZjr1JZohWf+GiVk1W4OYQkW9r5zONSc5qvqpC0asrUNffPa9GALNb5+RHDUM9H1Ht1jCc8r4Mj9+Tqk0WKqG50ykL+WkgQAJfNGGnDq7P+U/lBI5sdzei6+PYMS3Sh6ZRKN4/8Pi17Qg1WcDBhM28Q319xyCtIzVwsiAyvhhDmlWMZGNbMW3HhhJaAbI4xcNACTSlHdeHS9YNIBH2+dXXcQZOc7we9LvX1cKibH1GjmawncrV2TS18F2VZtASuQyqPjag9ldGTCwsrLnPLom92TQiO8MUc2/LeblaurCFOqZRCcVa9bdlq7zo4pR5ByJgC0URtVm6fepTu1iVEYd+jw7jhQIvUFnsUF+Gt/lhv84VT3yvoiNFs6zC3NfBqqyLvY8JOGPRjUK/PpAPh46XXdcgDUMOyQbfJnfm9gNRHb3y2A0zpRE29qkKp38Ed5lGDsVbqcrls8n9M+DTGqnLjt4CispG3tw93bA2Ma/sWdvyX12UjOPv5HQO2mMtCE96P2UugAFlAYAOydw29eeDGEa1fH/I0JvgMYwMM7lIzDVL/S573jjBA13xWDN5Da8gw6JCBYZA5/z+AiRQOi+S+Zig4IsVCzLPNMrw49NLGtfngVXNtaHFG8sMEvUvtczQqpAGkp3bpPxFAy3dFDGdbf354wi/K0QNQOPIOYkcit7ecPxR5ovL9NlKpI2lUtZBb/XPeFzePQVJncUO04ZqqU8avbvwS2B8o5Brk9XS/LP64j5XgZTzcy8/xltEPFkU+t1PMnfP2OuZ556zdZWLh+IM3TdCwWn0XvSqvX/VY+u9EKHbyM+di1k6eN4Sk3RwgrhLMiOZb9u2GosSCt/IqSAruexMe8+MbmK88gPG3FocaNDvwbtSR762fZy+5TVWCKL6p0kswkRZcMYspBJ6Kkz/pHfpESqjLgCgHjKywALjrhpH0dalciW32dNAhFGCYWl7vnEAU9bhJliPvyVtcRw4S705jHKVC0xCAWMDBLn8D5hsuzwAk/POkS15UiwIkW6k4j3iYXzooLERKU3/XH2NkcVpzoXpKhVI8o4EOfPVEV9QHBCq2fIqf4681o5VtuDWIcBIbdcw9ma6kOwkray1d9X5WNIt2kNB9taf84MApyPRAqsOenDxaq66Ws9IFT1cF9mxr90kQnFkRzJBAKLwCnOug5q5zDxqsx/TZXtdB5pmrTlhbO3qCOFrizmHNYYTzmreGB1pyDzJTzRrnJslP3c/jTfjcSdrcays6yPnfZGOjtTgtfsQWvwsX2fRpmi922pThIWFPSJofeDxcVQiG1ZNC6xje0sHLsKcyK2FnORJI+nOkNsS0IVnhRUXFK0UXiVGME0gM3fhmXZkKoo+Td23PXCqRLskqG1jvSnPrVOZGPAvBLn59zNyBgg16ocEvwJHVES10Mc6Lgnpz5bBLlz15QiSnoce6PpTcxJ39GofDNNipXcHVVipPxnh6EkVsI1xz06VX+g6cI5aMzq0F9NpuDMMzTUPksdBOuksyLO8qMpL9ZIAyPbaUWcnsurLvMTd+M4YJbDHx+ZpoQAwyzEFq9xomVDD/YYLdkS/QRXLTsncR4Ph0W8MKkd7Are7m3yiwn6lv3B5Wb8viitcj6eJvn/qJJAwLPf/4KNdLOBk2rS4yD4EurBogYGWJRSNqGSzJM2qExTgLq+dmc9ztkpPe+F1nQ1TrZWvVsrHaj3aT/F6lkwfyhR/tfdFe2yzmf60AUg2tWlMbE+9cJtcibBamivzL19qANDE2eZCGt+o6ZiD5CeFvCz297MoIorn9VVe3TkVz9rvEwb3TQnfwe7FeWu6lv5+Nlf9r/uGjs7PoEELzs4gH9t1hxofnP1itLSjn22Ngv9poWgAV0Z5amDubWq1Len4PI8NqGq53M20zG6/yTBJz7elAsMd252ZF8Aq3z8ejH9S9/WUIpdCR08EOyhDAVkJ+vala+6hpoG1TO+f0VK3U1FL3P+uxzoqeq1r/9t84KEpsTm2KxmC+BnNG42xw22miBh5NdCjzZE18/gpb3gS6ZeXjj3sr7cptXvRbXuNr8Zdeinr82lHLE6RjPsntRseuYb/3QNbGoF84hOjz54E/iNUaj5w6frlCsY3NZKGx1o2Po04Fln7yx2FxK43pH+BA0dBmU4fxcXX/6H5P1TJPE86DsUzb8s/ubSe7IXwESZtZwlOJ5jt3gT9bHP04U7mamAia0Zz6cL43PNuAavJ4goI5OaRxK4x3roa75y0CzkYAaaqYzdkyT6a5V87drZ0b6s6vrE2JF57l60LpOy2XFdX2Q+cRBnWnhG36Bvvb0d41kcvllgtIlzW7RnSAf+PyK4XhWLSKnT/36G8PBkvrzJIGMIahEijbzDabpTy6w398NE+Ptv4Fshsx0ghpN645kZvHSMA+Mjq80rfqNBJ3oLvWIDdPNXyTcEMLcESuh8MS11Uo5J2U3tY/NqbJZWvCMyKZC+jhVgy8JEE5JW9mz4HiHtRaRah32BBMLDdePQivh+5a85Xu8bq4h2hu0Gr+S8jYnkP3lPNKvDmN7Nnqoq86qUrpZcyKxALsOz2WmmekElYn3ITNrHcLrrB8PkxXl2vIfHwJdv/J+l/gXuy8/VOLMT6Hz+sF/l304BH9qaeGiJ1kxTFj9s9xnDD7HAp66dNtoLHe/C2nCAhZ7tHflhfyMaMkx8/P4EhxzQw+3CAvFzwSugAqH+p3aYcuZs8QiqbmniR2gwaSrahciYH0jmziQrR7Xha08Q0kyCPxrZcq1CbBnm73a9zXrj1M3ENd1P6q8MYIfmmmeK2S4j3MJOOme4npLChfVs5vfhx7PuGdr0yOgBkO3OXdk1ubQSJ/is5PU+fnKDrNuRtv6th2aBVuBOihf6O+KFAtgkhzr6qF4rJXmtNc+7d5A6CDqDPQoCkI3GvdMgdYe/O8fQJJ1+cDl88Et9eixW9mq+/UlN3vXTQJKEZ1jxxU5Rym0Yj58wxwduk/XEYov3wI3KJhuHABDew3rH0jLmTQFeuEF0tesXyzH202y1dc3n7F/r6Rc/VN9E+2eDnM8SHZY8Lu6m691mtpvvh52sv9gzGqQKAGjMdDZH9Q07ew+0iybVJPCAjQS1V34xbXM6CVsWpqSThRpliqkPdGhh1I7rBUqBJu/ahl3imfYnUrY8h6WH/dVvd+l7NU1zf2YZKjpQeL3iwhGYxq7Ee5q+cdpx3ECb/6iokWPDSCSM8SG1+S99itNPJaF8/tUmEQxmzjze10bmfdzBL9lvdXn0smczQ2M3xNBBLXupwxzUkwJqj3G201T/fG2fLBrGLiqveMkojT643plfS57LE49HguoB17yVG8g42uCPTCR7XsQuORBB/Xpy87KxKbhgMJ3fAXyRy5WFvkj+ZI1rMatwqpzHU5vN3NEO8UrGs1+8PfeViqd7I6ntq5KeVP8QxqihAM/fZ/9I5VGpejrf22WjTYGcTDBNNpa/b5hmowMgV1fka8wBrwvkr9JC3LEKLyVGNGNGDihJyw28jrgQY81X04EuQ3QmAfrxb/RGH+Kmi10ETh5gwX4x46kvJr9sIgxdZZKXft643EhvmHW7Lx+VntCm8XoV/co6SMF0745bEc94RtEhbamhvBC5oGzmquwC3szFtBBBcyurONHlhC08apLRmg/cyZPQm5jAUi6gs1zm8kmonPVbwMV2oSP2zCB5admY/M+TYTSteI4Rj1ybomJzutXiwl0Kvys3W3++e5dO2vu8Y/8p2xiGOnZ9wkKVZ6mvwMhgkT7t/NMaXmaPutPioRQb+D3c0HT98gQJI7AYm9OhqBQXqUxdbFSNLtgomQ1EYEtQZnT0NRahYBEwgJsmbLUvcdnplnfsLgSOlhtI7jT6JH/ZLP+Qu3RoEHQZ2SCZUrRON9RiurvwcDWLSMrkGS0GaQUIYmKcBn7kyPofAK1en6n0TohqoT4UmQkSblS8bvS2zTycDyc8zRIV2/nzXZd2scCW4kKat5u4cSVWWR4pmSFtfqQfhCdy/sDvQj/l5Mzs5Vv9Cy+8P0L1AAp6DkZRqo2JOJVVFVjAQ+/Cyb+PZPrqGBJWIN8V3P/MPvTu58mixX9z0Vqkz0h9vNv0aaST3qGX9E7viGJC8cmRp1DzvZNooXuusnvueyHerf04x4fKJBbkmmbmheMGsbZ6oXst5E557ybnNohZy8R94VWK7N4m0p5P3kV9C6HbYA563xVzk7nvP7ictBxP6i4uqlgqiki8PKhtg1yhPCYT/mvv2mWyfSWIfKD3WcAcKquaL/ThvSOjiLGszlK08k/9J9F4JF9ijvfzjt4O3p406N9DzQBNK3dlBUV4d2CE6SHjLHc9oBwQmOEeqLU9TuaVLj/pJt1iuOsaJz6XYOA58+RF4er/+QGvIB3M+CXBTJLoWtJTdpLrK9GPIC0+KnAxY/67//CnLxZcxuzeBcxhKH/uuxZJjuGRl8R+QADgz0t+12YM1fNGcKteAIcDN1YdZD0befe7QQe2mp30n3tVeJLfHwJFxzkkCC6VZdyke1rkykdlceK/AQFihTv8P6rTdM9/eDLpjyDLRiPoTb+pMZNpK3mCUEM4bjC+/gzCdFdsGj5LEqewgt1fR0+lsMa2bsVxvf6zrAlMUQp372pEaBKIXBd/vc7AfENBdosH0GquRHMWhrgY67l6R2y5poQbx24jNa0EPUPg8pxGJqXlcL45eMfOjLdZGmYTKCFmTZdiAfbU86g/V8b3gyXuWjuZDw3JO8LRx2MNXpsJlEr0p2csyez7CKsLVVRn1GannJCs8ANbsRnQS2+YzNbNSkeAeLPl7QozbfbgeZgz+2YvwFKa+sqZza3qYEePsur6Cj+Wy60i3C/wIPxpnLEhF48yH4vblfxmU+qN6ZE8PQ705/6ptA3AZcwAjMbsZn4sJ6pjkqL+/JyERtUy1v7kzXVlTzhF+av0Evi09N/H+3Wl1Jz+Op2mVT6LOzJUNv6HL8069IZcaFLTwgMUnu+nPR24ucXibt5TQo8gxVfiHO0xopI1Cnjz1rpoyaoX634krfqcF5cSSbEYlLyNmi64IIGgJbdH7tpYZw5C4Q6Q/RevvLj42F+91aZ8UdsLW9MBp6WUV4wne56f1qsSrRAYhP1jp+Izi8+25kvBJeVlTT4xSQH4cVuR6lG1uNrg/KuM4Gk+7pNc9zDXqU13F7yV8RDVWf1NSplymPxj6/8DnzO1cIzZQX18Ziv9k30Y7XfwGpgHnEKNmLBKaiE93tZ3frvQnAHxgLkq91M9a5pX5/0/DUio5w2XViUZoLZ41pTRX/rwhMG3+1T4z2UqnemLm/6IwcH0bBTI6SG8em7/UnpIVUGusPiZ5muf3YkjYMM1/KQ1RfvtG3lpjBX9jRza/wx+ZDqAg4Hl9/Z1imqt8aJZGXVhyoKxq9DbfRuY3vnyO6ohIc8LRSLAqb5QYdfQHssFTxb4h8q+1p3Gmolxnm1QodorqtuqUFtBZB+rR2ZlDrJUkVG3revB84btxvk0tm4hb7qnHRgAZ+NLMLWjKJC5DpekwZ6vsSbWLl1IecbdWVaa7yCvNq3pE+SXHaRWQV2sUx+sEX3J8a6HrZbc27HZ6GS8w8126x9ywKCVvwzx1lkb5LgFdfhvgfDa9JOTJcGmCaxbJlTaoSXXNvMMVRuHNgHttAK6NJRh3g9DHGp7ZGQim+daCa8rHq+rHJZLfBEIn/AtPEbUBS1y4m+MHHIuxxPPcmRjEQGvfQqVrmWdfFbe7FVafg4c1ng4TAWYKh8wHN0l9jfLJchpJlBlXys9VrOdJwU7HohUpvq9ECkKoLTT5v+QYrqHqmHutfLb99DZxnodpYlquNciTXDyw9cpCbUmWPntrNL9k0nm/f6Y3cLPdY+NPOXDBhPBIFdSyKybdM065JCpz1nVSqJ4Cp+aaZUyUrxNL41RdE6M35ZzqyRCvvmm0ociAgSVyb31VIHc++pDq5rBWIuYFDrvxLtaJ7YnBHFPgfaQ4VpG+W6crvsGoHIoDrMm4aaLCHwzHSGnRnEBnnaKJRynIRp0svjG9ZhMxAzSpTjAj9qYDCQDPeaGaawCZSZjaa2prT+xzujH9Bb/sZ+hoC74NwOUPn4avDgWsgpa8Jlllb9hexcO1kjRYqKLI+F4TLSRmP0teh2zwQN5uykUXRGwNcmyjBYMnOT1pQ3e+upPA962/NGBQuQa5pxGWMstXOB8csJPmkFserGSMn7oo+CgFeMJW2RCTlPf912XEOnmmWEK5adguKb27Mmfh5E83tM14ff2DIeaFupNZ7YcFmYfPP/FTjSLZDRu047oVSzu4EFxJkSagvGRt6yM606b/s+F4K9nXX3iauvZuO88fLLAEZkLcSHNYHTxHLK+ftSX6RHpKEzj5w3jzydc/MVDnPFrtyPM3orm7bXH8uotXiivziw2N6mdW/sW+bSR1J6KWuwj8Zw/YxN7Yvl+nHvv9J+hSiH8PPZusJiV20+W/rCDrNSV14nJQnihE/SPljDaVlvvJo5Z0COJZFlILTe7QTU8fQSjQdM8LMU6DGzkOknG7JFzziTrVrm/6iQI6p/5EtqkPwJOPljCEIgieOE10wJNoiK2xpfbwarVy3vKqg7E5ZxFEJZffvCfff+qe4PpPrA2Xq4b6hPcoNaz+K1A/qnuEr/HuG+uXJ4I67nWzqBSYA1x7VvCEdn6+BK/3o50jbU/Uj4PtxzZTjJPZvIn74qg/EWBwQ50DBxxchCxAWxgL+K3vp7iV/n0I3PCxQ8KgOOa07FEoSVE2pPkuTPvQg3F5gi/DAUqjvTJ6KVdZjcqvH5el5ffZm3+V9gFzWsqnW+Z26ZeaXUYTw9q6z4X5o9GUGnJauWJRWx0dGtCa/xlO2e86bRiqR+3vu338TocTiaR96Wjp+3WElNK4H/o+y4kH/CepBvnLor8LpeWtyWFOzuRHuhufLgw9iTa2dnsUWK3a4X1pp83Bx/xzLShWZ0kwmcv3ofn6rz/+WNn1evAAu/a6BSvg/XIdgBV3d0yQgUPurtABd4p8gfqw6fNH4Kqp9ZjJ+Ys120kbw0xCigeMNn6psNVX58FHcAHsUeoRRerkptgaaFzSMLfeYS7NisFZRyIrdJhBv93isGISy4DwKzk+Lj1BozT173qmpc1YzPaxvb7I95XmO4u6W+aJataXoVloeEFC6QXQz6rJ+lOG38pk6mlEX1WvzaluQAU21OC1MNvnUzvq6Eu9Dxfp8oX4IAl9L1BESriaDtywaND4KgO+fran5vOuqGEV/EYheerSlSLvXTaEotAy+GQRkf6a7rqH4wRzw3rnTYgjLBLEjCOKa10pyeWUF3itSq6MOTAZLFVGkMaY7LefOjLa6Pf5ZB3xs1mfyCM8bO/dMsW+bGApx+l7PDGb98wzf4Rbhmbeo4NFM1d0izr7+Trbx8WTqxmSAQFNHZkKIKedtT/fbmTnSPRdayjwMLKJl2I4QP8r6w+DYfFBdo+1J5wzSPDQ3J/zGYZ/PXRgJ604MGD4G5lL9h8u0XdL3SvpBRFsM4BFf7HwIPGoMde+Bz5TZZfV5inwjaZecWPiN+YQGPGjYaL2RAG9lQ7RbeMDXonYGKMVFNkp/xDFoIemcYFf4JFCP1OIhVBYVUmqFR2FTmBb3IPN+eMGz91nPOaiBsSoavEvOCVaANHn/lV5E6uP1J+ya6oPDnnpkR12lisefdpODuvs7AhpnAb+v4O289IUHOeGQsflkMo9Im2VTem8T06FEaX6ZiVluHWEU85kvRUvv1vatU9cdQ0QJXjXfHfugN2sW1+up6Hip2UuSKwUzIS3FDyfybb73lcn8XxjRYy43ENmOKraMG3UzZUspWNiI8zw7eiNHXyx7aT+t/0SIphBvWDLo4qtkjV47fPzx4XeO1mI2ST8joS4+rEQe8lq047m3Jsn7KfJtVWJ8/1/DDEQbXEwKRKL8ks9JykZRVz6hy2xfm6mxL1Lg3LYyP5rmcm6SCVb93gt+2THEnQ0yNRnPTSRjAK6kqx3gXHIlvHq9ndMzyRzyltTZuTyYll1jyNm5w7tu5EMqtUCWSy/i75NRgDql/AyNITwt6cVHcZviWVH+Ntb39/qSdaziP+00RiHQNvcH3ArRWhf4e48syyv5JKlkq1nh0LvWhXpN5RziS1vBgU9H2MWXdNApu2v68O3eTIufIKFamq1TorYqd6/XdFyJUpSL93uht3qHNxFXdPecJ9vb6ogV75YMa5TEEY+GhiS7H6arQieHxgSzvZIjdj30/KZkJJ7l9yvR/yvHNp+b5YVf9xv38s+iupla+k38hXdrVyvy5KT8zZseKnyLi+qqfRUntfMpJb1lva8BU5cMOzVHlz1fbZCiS/Y5cgnVmeupkDNxCizcS86jEdlnCBJnvGD0vKcmiRZaDSdWkcx77JGiGTdr3/3Q4VQp9BC5JNJ1s31EUIHVuWLAQGFccq/S9soR0J56dND0utnbzqo1IdrOOz/CcddlG/pi7UA4K30mKoZ4N5Z1EkW4q/mpDykzkSCeLe/+WzVmInRLy2xaMU1NT7mGNZGCayjcJ8ik7S0iThsVLb81FWyf+TDOUftZ6xy3+SPyRAlWs8H/dT2by3swq2fOpiJoz4nI7u4t7Ga+jCvgCmW6GoKhHXcJGrcbHq8aw7UNLRS/TU9MEYypj8tL3Ug0pGUx3RD++ST+nXOlX+FuYqGWv77QLXEvp/o8izRbYMI+KZFVPCDgQ7xGhC5Ir8PKeqV1ligPxtG2O9JVlRpyP+okjyz5C4V6QelH1goIQsTytLLpRFNmdNfX5CJj9pb1Xr/Mi1FSbowtGXK21d+rxqoPperHn7qoLprL0nKufiSs1Wkg2chNENbHFS/86pqpxb8fjanzTPAURu+dBeZVPajFQxbjL7QWQ+R56umsssjItsqMmJsUvNaYcf9n7YpE0KbJagzjplOlbFAx80LnR4ZG5eCPLmz+9K75kmF/zOs93LcfZtXYzbtevmU2oPXGbJnQSxbd69nhU/JX5cvHo06pfKkI18URABXOavXHhrkbZ73yFXKbbmW1Z7pPnP454+DJpOS8K1I4xkTF6+M1yTb2ja7sGVUpTD8o0BxWFMyizvEPqrlz1dFotITlrD04NllAO1d7zUhUApYORUCed26AlETNhX13pr+38KAM79glPcxE59s9atGPOy4jYVcS6mj5bO0VF6czBnLanljDebIT3YdWb/tOp5p/Z/3ZKFwUvcjR9wqcvKqYO8IzoW2u8LoyMU3L81QbyLVanaiT8hnxTxZs6Jtkjhse9onq63gdEZ7RGeL1iIR6UUZmXckkNO/e+BVduchPmUFtlEOrMdal93C61maiUHt95976UpXL0YAysCxOBSO45/TS7t5F+T4LxkoQ8PgkCloeuUXzWLqugKvy8/IkICtOrHr4fOi4rbOA3mRj8jl99JAyWW55v6XQY9u9jCub+LEBIUpQroYWHa0Ts3sVMWnxYI57jWoev8e9rLOBK3y1gYcPmDpRimeF/Fsnlw53rqzpezqCBWKjEe1+Ujn/qx+opunXIsUWacRvptKDY+/EfpTngjxJhz4bF6YAY8WZcdhSqPpGoh23iqoZavdllVXd81UboG8fbR13Dro8OUb4fs+Q4ZnbjT4SsRIgIJRdiO8MkK2Iy3Fi8UyiRIqWI+FjBI2osoNbUkggLSE0obblhbvVAfV2HmdjTMguxlQ0tMsjhIQv/MyOPuC8AC9Ba8fv2vjVGG6n57L3B97Owc0leahthbhripyTBqdpXpZahk+c3PykDTlatPlpTuEwgWZ2YskUsbMMnNrQLenRbJWh/9/4LX0taxQImBIYTXn301iIJ5SF+bQo8AW1pY5q4zuE35qBl3LsHcKiak80+mPK37hAw9n2o/6NE6pTtpR6XZNuncYnK8zJ6v6A/wRWpY/jDWx0Qq+2Pj8UFCgrCXwbWVVUzeK40kGABVbd1WEBIylTjv0kPlYy13ZEnNfvU9pud7lDLMEsvWd7vF8Z/JjiztcLcA0WwgMaxDr9bOass6bZBBd29h8VtjWMky2CqVn1LAkS99vMDSnCw18M23v3oiurvU/Re0eM/BFdUS6Hc2reOW3dpysKmVE0vRdHIMqNut54VnB6dq5TSr/FlGeN4mFAPPauCe2EBF9O3BmNSDi6/xC8TOkK5OZa5j5wC45p9/Je6PaWT5NJ3UhekJWcIjvLUarGAZwY1FDtK97dGBvWcVgjQG4SSh6Z/9sbE6F3B/wRnPjxWZisjvDOc/b7/CDRkLzHj9crvGKWAb77larBkYks4HZv857x5N4T8Rrl0LtH+4fPfcMqVsoq7sfCKeIKAdMG75JmepXm+gDk+sjp8prvnnrwflSUelCHll4fxgWrmR+7czyutnLUmaZpCBXVloe/17djibSPZ6Owg5ZULZd/Wxh1nXzGuVJl5Lxwd5vHG8pH5cpS2JBjQZMOG9wa8Crtxe/SrCo1XV646Bxs60FPsOvuMGU8aO2X6SxWCqpe35THwAxfpoylZ5PJxPwFPP7K1uuzSTd0iUXGaP9x4gfPULqWPJd8LlEHevfESIlpZVM2q8Rt+Ezhxu9mu+ajPwuZtVn89K88K7ctLp/xScE8Ys/YHIRBQbfDX2dUKhj1KsT2h4NsJlaQRk2dQGi4Kbu6MShB5A/vthMtVZmRFGV3NEpB1rvjazY4IO6nxpzouXhuaqsLDfZ0HZfpFpVu2rLn98Ya7ccz1f1GeZU5SruqUjcTkMdQ/QsM/0l65YiSru8wUEuRein53fktNnaxmxOQ/yqOC1rRDTPSbQkorXejQXx/6u1AOpAn38jRAGa+ZhBw+0ugGEH4GH5iZX6BzjJR1NgSemltUmZ3akDoqEG1Ja3y3DjwBHB94uXQ2wYkb3L2qV5I3uwOna8FisQcsnjNYgI7FkdeL+qb2SNio6syvRyuFIN8uLABSs3/CpaWuMGcLJxYBdcS+QtcHsFQsB4DpkzdMUjY/pLKSZwDztYPOsYBj7mGGXbkfsTYr/X6H12XsT5nRK7/UdG2xAJ9/8UHl9+m0uJqMRq/NQq0kRj9HTdVCy5RWjR/BVUK0zkZ/Tdjdd0taHaE6a7DpFn9ejZmQW6zG36z8xrp4f8wdZT2/w7hofi6X3hYSd13ZdsRyIIx6k3XMndeTEGDb8+RK3SGTOylLiHS0AP9YBwvgf4aE32EBT3e7FAQG0Ir31/kIyWPwlix0QLulIyOQwNso3hUG3XqB7ze1jcpJnWR/ZzzXl4c+1pONd3KF6LSbEGXOUTLqtsrZhOQfC9KOui3OeE5GuCyGvIvZss2bUlmkICDjujW/NBz6TZhQfWMmchSeey2bLdWioDUWeJw1oCmmZOCbKnyj4ttrhNl4nnN7PeamAJPlsChw/2Um8UDbvfBAVmrq123KjI75JqJQPZlbfS/ad6UHqLN+juYxvkJK+mXX/ng/0mo9sxV0ta+Y7c0aFDtMF8PKA2+B6XL8WB8olINkZM+kiZRVOAXRV7xC8fh+o7H/nDqpudb9M+HwgAtvRtedwvbdvUlVsBAXnmOhyP/8gpT2//q3iye6U1y/i3/cA0PvZTEbECObvrCo/tBc2AnRDs4ij7wNXMWcSNYwqT1VL1f3bHg51ulQAOwDnv5sKt+kT2EZHeMyMSa5F3aQfxBQJa0e1dLSLZgV/O0Jf3v0As/ZyglEKjkAc0zlYZNXNBWUHVR0HFoh0TKSe+jhTgj3bgxzyIc0dLNptdBd1YQ7+5uZ8Cxx49dm3SygzVu2eA0hU1iA+syROwZKn2Ni+C5B6pNJUJjVVFtg1ant/Ev3mnffFq8LAt89y1NnDP4O1uJnlRgzHezIiX9b92PJs0Wur7C+NVh6qMaG3USb2d9ysyRJZYYNyPaRyaNJAQsYnM5/O5P81I0Y1MEifi7K/WSl1ttbu9Px5RxSvvvJiu/5OT6ZKyONYXpQRFT2hVXAR3kfLCDITejc5cWLK67H6zPzVHdahWsQEHIXOFecIJrjGT3/TvvG/0NTF4aNvFwihO942mJqPqJhfh6z2duT52Q73wjDAl7ewTl7llmBY7xxyLD2TupOLOCzYv6+Gri5KmpHCeTQjAUc6kv5rC+iSDN5akGjB4m1JUOv4AFZjNPLLZhhgy3Q46HFTKtnzLIK/B1YwFFGdPs2ArkU5rnyRvmy8t2hbsqFsUpYLBABNm+cX0SRq5MbmlpdiNhPokR5SMFrP3qu5iDUUPS5/qz4WXfkqFhAye97UmPF46WXybF5spr09JfBLVbXNmOmmtoqejE+ofLanQGUL3HQM9BD3c65psjFvDzqv2owzNNVgY8nIstJGEnd0sjLmT6FzTEiWIfpeNTFumHRXIj4k9ujk+kzwrsZq+U8WrakhjWSIFj+XJRu/nlPq7Mv9ZJVQFT/r/y2zZ7HYQI8WIDeG4S9kmtpDEostHuWmemOlND4DAKcNU/6DUoQR5r17VasYAHrLIXgLNz6HhejduRgWm/DeDxw48VZP/5+Ga6tXXSuO3s+4PBxTkasN9TXJglNbfi4YEMPRU24/3Sa7qZvF2O8ko+0bXL2QYaRaBUha3sweGFAEhk6DQJNdcVHG/KLZfeEoOF//MaUgeEcnbacOtO2PB1KAjBJyu/uMoId3NaSHjoM76dJJ6KWS75Jh761QmkaiYCKhnzZt2+wgN/8SZHTqhehJct7Ah9+oAQ7bdIzSYJC61nRinou+Y+5bhvbsIAHUSge1tCNgml1nCT/Q8ePU0ck2i2hPc/ku6mcUxmgDS3EMspYgMOPENZ5eg6JLdZmtq84L1/ltVgyekNyPXGlRhkjciouzxBHn3JCCUJU8JPtky13r8fyM33FvLC69c8HnhTg7uKAGmGxyW6FuGqdQHsyTVYAG/c+wR/s3ZH/J/IjMJkEgJkodBMQZSGt0LMDdEeGvQ6jd/kDgk2dYgF4MZgm9pZPTdkvbTLdxO7eKuvqm71aDUfANTCTv445yoDHG1gAol27xVhQusZXEAvweAqC+3hBW7t/zWsPHfrSYwH0q071TiOla+yNcduNP3u/HuWKnY5LMjjQolwy8n8HfZ0XkqHTqqVNfaMr2kj/bMGBIdRZpLtufXC8AniMC2u4T+r6fnwHZ5beNykK/w9kOwslhYybd9CsLdd9sEXt153g9ICapqsH/HxfRwQWF+A7GiPnX6QFgEnuIKs8+sAXdVaXUS2hE1zAIL2271hA3uZ30bLq6iVSoVm+wlNmJBZQSnx1uG+cxf8L0qvKY/JpwvxF0fHfcQPzzBL7itfd32YuGsnCmtrs58nXFPhzXLubM+xbPE4pgf4oLMD09+xrl92QVJV38geS1Wm9bIl4WABQzZ/VRcTnpp0i7EWehYJ8At3OhylzJ1IWqMxTRquR1f4C1+8flQLGXaisCBCR717/bWLurzk0wsQqGmvqLvnolJs09QuoR39/CGRI2jZ9dehX9irrboD1BxqGc1jBtJuwnVH7/N3Je2B40xBO+zmCv3xGKY17YFjKxzaqFQlMpw4ED+bSbPZveJuSrJh6a12Ir/yxgM0Dq+NvTBj7agu5Bg1gSvEJFmDEb2A12zP6j/VvbXbLHU6XvhS3X8PtUxT66JyrE/LlfRtkw0UOePnoNE2vddwGHlb28MSdg/VqqLxoVvRBPGjQwge4LKymfYFJr73XhuoRuJCZPnpKuh78qE0yAQuomCG1byPdUaL+fvqBd2baYkYHtOWThXmAozlREfGYJo34gDmFozrQdbvl7hUu9hmn7/6ex4VyrYasBRG1MLSLHXlO46Muy17q0gfGv7FNSH+5nan4gb5HPt6+KySgw1QeGq96t1SOBSzpb8DcnJRRCdFhzbw4lbK/JDt8XXaurkCd/m9lOZKz9DuP/qe2jULWxd5aPTlJnLyJG9ARr5tOx8kUKQ8Uh9HW1qGhMvpYFISIlf1uov4kZefNTN4hFhDKbzJtk/Ay8fYDbcwv/BpttUuFzWUcK2c35+SHygIRsW/hVMW8D+L0pomDjRXRht+doD9yfSahXLEufglgkayxlYcfJSqm9qOyCKiAR+M9MMvP6NoaYlr+xOIP5P0kOcZe4g5yed0ZBleVC9Q3S4lpiP2zZ3f8ZqUrEdFRl9921xduWHccVV0vTZ7ArkpBNpbJni7ceituWADdSc8GZ1pB5+TyYTGOIwamswZJgNvNcUnIB5wIfST7OlyxSgNYNE6GJNZZzq/T0M/rwVTkYMjHVM6aqdkSfz86xgI2ODkRjayY6/QMmaA1HKhlhN18zYN4ZozZfjBuA/mraCxAZSMqwteVMFTs2KhGDQ/cYv3jQMCvas67ggQv4uYOaWR6dyndWn82dLle+gLHNOVGVjFKD0ojeojvMyFlH4FPBKoUsQCNHWrVjgh3TqRw08B53YLg+T3VSr8sqbysn1iAfaPuiPsUfeR5HypV6JjnjxbNe7K59me1GYRuLZEEoP1hEKL96+E5iLQ04vyx8t1TUEzpyA7jGi9oOMNm5sRq8Mmh/19IfHO3yrsNtYQOJe1qn58nTOTLw7SPwe6EyzVbtzaJr+Rt9VAa6/6Mt1XGVx3D9G6dQQRwlKDTZNq7g6eHdAN1y5bqvuXqNKuUCY3y+mSnrpYUXgQ7/+wLNmDc3oJoN37W2yfrzpAb4675HC+RpHYWstEKQhosAKr8z+WLWVyMHV+WHqsY/lEyDH/Gv2YHSIRI3TErO60yXBHikgyB0hisiNfv4jN+nef0LAE5OHvtp1qYyvar/XqY++2DblCmtJfgCmzfzHSZATVtL5liPbP9dnULRyGveldPLajiytkeHJcCW9MKIH7i01NtlSP+BgEmppKsQN9IIpbS5pwQnvEw90TZA72Zb/7S6+y0L1hOOB3YhAD+yhNWCuqiCceN5MMsKSQ9H2PwCBm7M/I3Evxkpa6BTWbL5suveIY9n3zsjheeplzjDfAKaZ2mxH9cp/HPcDIuEyIDv5Qo/byT9Mcjl+Zc3EYOx3aJkjvPRPhTvjeaSLcIzHc8xnQFz/tfWz1WkYj8F/oyCaGrXojw2hej7og4p2UTPllYzSkJQAe921f/xV2zS+pP2bVdCRVtdrgv27WiNcLekXi4sFtA2Mz7LTehseqYKYPPbVel+bBlCHgBJ0RyItJKLxirS4wdb5ofst1Qp5iTDMrYjLBI6h/bIbuEHjIO6E8FaPe3ePfLtLTYqzCFuD4V5T0gK5PtPdTdG/kpmhB2BMewMjs4pMuc/b3Yxsc1AhvPYR6biVloS6MX9wUzWV602SS0XTxh6iJ22IlHr3la4lr4R1hAf8wWvfrtC6obxpAXm6sNwEAJ1i13r+6dn1ZRdKYs/N2l90SM5EL4PiQHvkbvfVrFVHdJJQYWH2210/HUnQS6qPPU8j2BMo3hPu8eJBgLmFbRZqxKh4V+jHl5Dbl3m7PS+i7sZFPuMixRzg5VOa23kfGD5EVPw5sWRt+2ezpbL8McI7VHo9ZTDrWBxK5/1K/NDgNU0sYa6HMHiMJQnMAwMRTRTWHKNV1ZR56F6DFE68aWR96GL9+zg9ruCBRpcE2qE3hDdNRnYjTiGgK1Vnb/nPTWZrEbltg5XzlxFjvxFB1lRJ59du3Cc0rOjTwDasKbA2QoL0VJob1/e5yQVJVkQ4QLA7CPgt9PW9JhO9odTVGseVK6W3beNbvfFCsO/I6fRB4YNzewxGfwQE85aDbMuiG32mcp4Ok6eGKP03Z0bVGGQeLfwWwmg90dCcz+7XzZCm9jGwLoT+FvZTtTfUIuhs59qSWz0NHPzbQKc7m4vFexGsIyt+nS4MZH7VxAYl30yL1w6wh0MppNbyUhu+Dzc+yev4BjPjn48n6gqeT1yfnwyvNQnZ4YkE6iS2UDPO8iMoU0cHuir4dc/jqJR6TdONdWWZnoohwjuruVGzC0Ye7/gVdtvTeMx8T2iws5X937mMlZm1xtJfM8sorvNvuxVB0pnFwoziLlzYCFkF6QVHZA5MrV/VC6zu0Q8U1jIVD9iRKw/c/6cILAoiiOpdvtMLIhkcD/jYqzjGqj6xp2WtpSA4q1eHAtUNwJheJW3L24u5O2lNJSILhDkOBWHIqVIsHd3d0dYm/u58+3vh/Jysqak5k5+5y9r2syc8ajP16P70MU1F8Z+qZ+vil9USaNAfis82V9ztCLG3H3JpR0bv1HiLpNsbos+VWKh/iwD9k1cr3KS5D8HciwX421LfANGUXJ/dA0BhDLwBD9sr8MhBNxQTJt/ayrLLiH/X2FGRYlgESEuz51XLIe6N9lAUGirWeIa2xhfeDtuulwGZDwzfqo4s0BYSXzry7Gl8Z5PWKKlCToxnJHE2+pJ5SNxvdKbUbgFfcj0HD4g5K+LAiqFLCWgRN50S3nne451oF0DJdkbJalVQ92kVBbaGzXaHn+U+Bu51Hd99jiLtG6NgswvJxLS80FDqYpJAn/TuojEhpxYVVp7868UzP5lmn3gfMetEL9siL5/VT3ouOFzfcvyk1TGqoyiYXaSf/ftfHvSRGASv709xW+BpO14WE5zXEKxqdPRy6xs225ZV2wkuPs0zf+Snh/JLjwqiDSQW2e7LXh4IXjmBrzuUb+4jngxdNTZat6926NGe+DgyjDc0J3+k6chOeUlD8QXRuVQ2k+P35d/9gMOjSBQZyxDiIapc/GoQQRz2iBNQfrb2IAotG+g2MjTF6/kgKmDjm3JYGup0rpseGjV6XllV0Py5fCaiNFfKPE60WORshoUso+apOyNIOxQJL//m3zdwKxpp3svNQbotl9ubq19bzBN6WJI4QVfHvTsXXOuLdcXCQBZPchOkN2hngYwM8suYZU57eWzlEiJoNHi6y9FTFBgqE4Pk0hRpNyKQUlqsE5wp0lZj9OjiTIIn/N4C7zqb25V8PKjF02SA7bHT+Qgu9vvA86rr4QXBVgAP/qLTAAnoNI8MwfLAbrOJQhYtZUk57kFMR/KSaYLpSvc1PaZ6sNqOcQRwoneM0UIJ2TMYAIGAYQ5u6+YAKKKvrvAUWUpfS1G7/4gpM7OOOaXIC9hxHRgL8S9gkartd4510HMjJD96eEUO+b1KV7XmElQIfbGcR9sC2gRg0G3T65t78gPh9qQF0voBysJyoxgO8XOOg2ALpuEPyvZSp8acqpnYxMC7z2cOZNQSH2aEOWc6aK7iub0c9yo5iqwWAkTomoC9ZBQFLXGIAp5f0YKrGEYN3qpBXc0ySzKhHcvnWj6lpxhmIL/4tmUG8WTMcAwFTgw9rWcnVu7I/o5u/8Z1Oi2+PeKj6ut6/4O/MdbKEsoFNSgX7IU798nrpD0IskIIITt5OGWy3KJSS5DJTPFZBl5oskRO80Y+F+lVpkXADnplynrYqT59IoA3qb3CNfOTeB5MigIIicyGNZC7FD951VX1yEYP0LFWA6Xmh9A7p4oYG2vcnLRndjjWGQlx50sAT+F494bjFy/QF8s950PdHiJD8Y14BqJzgrANv4dYEHyuCLpgRo9rRiyYFj8DZzMZgPMTYG/ifG4T264VreZk/wnSoDbA6Px+KQQkXgoSQvBgANXAx4sYLuj5n36wo+UJXCABZmQQgBvdpk7baTW8bzzjxwgNBIuCAVBmD1WLJ3Mvz9iAkttETodkbcWVxnrPZItv2oGopKS+NEKoSD5kSTJ4HoVpDjZlh/c00uuktlA8EAlaoGR+FlM3t4+b/ZZQRO/xZfIaaFz3rn0wyubKgIhdABA2aMkFnJteh9NjnQIAaAky1KZIV+XwPJCfixm7QDqRoGrdr8xs8pw7kwcnyEgDPJch5jh+bB2yuZq68yqtonJCw047Yf+FkDZbwkoxS8XvgMW/5Bwm/1OJnzxR0Rs5Wj4LpHnzVlyoz6Fx7dgq+j2RM2kLDGtsO9kfAjuOwfYPKtjtgJwcBm6dwzw33BOyKN89/ihHCw0vAbLbZ1eZowfSyuz8+c/o4Wa3olpAXfW4aKA+eQH3JPSpEvS4F4+/fdJ/M20U9zln5KOQ8LZqWwSDgW01ACMvu8s25pNy7LXvnCeHkWt3gH1ZQ/ZWxORE11+Slsx2qfS3lGJDI2yKqd2Fq5+bnQSh6tInFvteDhDKAOP/gswWmFjarfguBIvZoZyJuREfqvrPBHXW57k6p5JYKnD02q5rZHZPXM21Ye+P1zx7kAziUOkn3cLwQrwO9Q79sKMYBy4wYk4zKtaXHZ/xaR4WnRKAdehWuBTj5gydtARGgs+AQ5FBexj95Cy5t6CX/eUWn7KBa1sqYhGfoCn/OK/57Wdc/4l1+NJs5O0iWB36xWMlz0m30d9/HEBTZTZAZytyY0iaM3vcqzpUG7tJL163nOT2gulh+cYO1gpozw7IWOBuRI+bPEPQbAbnarHxArvj8DvFnBUtyvgTu9ZbidL9gXSWxfq4CLbFORrL/F0nsJX57R9STBBgEGYG0gs86JFSBL1+4v+aBXrtRu3nrIh5A9ncF7+BkG8Fkm4uQW3MGPH5m6oQE5w4rCmXaerPr9U9lbOXBPdfuaSAsLaOEl+ASKZs5qE2k6KSq+7ybH7sL+gnsLqbhlggEQ3DJDr+nBI0jwTaf26R6P/E0ltuB5Wd1Ng5AsQhKVaxhAO7Y3wxSB0SlCJ1nzFrvaLOekGu777cDbhwlm8tjdC66ofgkXcobcyNou2jGlv1uSA69s3GnjwglpYuYgKkkllet7c41pY/LZP8Hldktcg8NTYkkYwG8XOLK2ngWNTapXxeAqbvebbND1dNF/z/R4BBhLhcQysSAZZ1jQRlixColHsoO958JPxH9F5Zg1yLhi85PsOz/Pj1Y3WIM6OdKjYW7Eg/IKXvNw3+pAbpVTKvCiYrD5/MkIOkzp8t7YJ1m3neh9jgPOV0sn8IQGyg7dNUmArIGg0eUfxLUxgIueFTS26w/GIaSS4CkjqGU40n4ZCl19nZy8zrgMnDQ6XpBTR3kbYjPv0+ui9vPdwj36tOog3bnemloG1A4QISCHZk38seD8EPHM6D4tvXPkFFsyhNsOsEGix8nZL8VKveYnX6ytUPww3L8m9sfaq0Nd6velsb7a9qqdrMS3WXTYeibXLs8c6z34ynBe0GJYpbz7DUQZ/VjubAo0goxQ8ubwJxnMcnL8989mPm+X78vHjseXw4NO0zY8CZF37W4738kOIDIzAoVcTZ60/yxwZ3wviiYM27W6BoPDgf1Q3gsknkRZS0QlzOF9g6qzYLACqUb5Zl3K26J+SMcGxGFCdOgOA0gufH8UzU6ZvtAMm/N0Z/w543iZt7TnQZIfLN+Rd0DE+mn8OIXmPeFVKVvegTs0Xrld64gc2J8TbzRp0pCeLBP98zziffk+C9rMFklRunhBV+ipSHf2FuwxorkxLejwO94vxUrU+8Iqy1n9VpduWuChfzs2+u0FkKNgmcLrsBUUmv9ufL9v61yIdlLAWXTftmXCZcyl13rphdzLiHcLHiJMbuCXU9/PJPppnFzeAJdHMABi48G0qMP8l8kNKlbmu+hAl6hwOa0sglYVcZ11MnzG6crrSwPxDUheAHBHVecCV5UvyK8jvoyI4BYbi+cBfnO4+itoBOkPcZN1LuiCUMpNPGg4GU2EAbyqNNG0AR7RA7drUQ3QVe5PXi82fsjhDoNIsTFMFPd84tmmPnFPsQ3/dVUzfaeOmD4DopK+n6mVYEcRXgb0RF96BcEpYHKDfHw43CTu/gznJg6CsAHfX1kHuT/DdnQS8ISBYM+YG8mox3Iyt8eNvk4nuNSQvz5WH4LtlmMALnTgy9eFR1D3QL7RjbMuBrTpBtIXHKYOjMqDDwS67t0cDLXXW4ACZcexxZWNHQNggaGnakCBH+qwacFYpR0hkrcAic0qBEYOAG+Rn++RB7oT3eeSgkP4yygyKDKgJRQhoyrh5WN24woDDlJIzuQLIRuXCxENdivDohIl+1Rl1znrPb0LWztT6aTWQQZhwLeR4FlNzzu9788u8yYQSnzoQ1U0SZsNtGcBkY+doaPALZbLvHnZS4pt+T+VERoTBGGSkUfoh0XL+z5vPvdwubR071eJjkBvX375DmI/y0969S6t5MtxdeH5k6wZ3uo7kGNDrGds8g4GQGM8vgOxuFBu2hWtT2XKhDVYISSPXrnY5U9MP+M5HKue4eA8dBmUzZWWBzII8t3G6+faS1Ht7P5dTx4xB/8I1p6s/0O0YPO7idJvCbmX+8lnY0syL6LfMRbSGno7yvwo+JS10ZPfJf9wFJgkB5/Od9YUIeMfXbv3P5OcAe6clWl4kxmzZ2RtjlOWQU5zt3qcnZxMFtsKHa+9/+Dv+tJ5z+/Mhat36SmuRsl2siueV2e8chxBjpJRbezNNwNfKl+XNg6fsgzjb3zGALQOThQz+XcGp0ac6oJPi0tJ0wsUVIzweVuoqCLGy6J/50awAv7fy6pRJ/t5QGhYWCm8xcoD5Md3Ew3ichy/an1PtHT9m9G78vUZ9c58RQTbVcmuh25SviNbKj9K+v3f6EVs0vT/HAne7SnLOy8Qxf9aQf4yBJj6F57pVgr9GKGPLquDMuBlU8VnPf6UtO0RSFehnvLOQzoJDd3Qdi04P4K5RDXYIfcXZTXmMlxwIsHQcsHpRQfR6/RPuH0C/cnAw9D4e5vMnxLqUhPJSqNlTp874a8uCEqz9NGfpnOeP+ZR81huGSfOUsyf/H7cvZQ12cT/WSv08dF7VpU04+jLsNZiIa0nYiLX2ROecvuW0qEnCqrM+0L4l9/FfJvy8U5Ul+Q8pfCX5E6UVAunQzuyHy/J2YdVKaY9PEyGGIIMIzV3lmOM/RjGkxnG84bIc3uf+fE3GoZLJqzOZhMz/r2G0X/et//7yeaXsS/xBaxvBDycYQ8DKr39uv41kA/nqsQwKd6i1Ihf6HpsMKpH3yJ5UeijwwqtRrQE66MRlkmvJn5VTUdcT0YrAuKssvCCYATQzaFh0KxSaV/cL3vfR16YeYX8XqRC+1PwSYpVOd+HY5Xst+8ewI9foa0E1G6GE7qdnS/U3Q6ICDzcQChv88d+lmJnP2LAG7nldhrPxK3zGFaPUqHncqDxzIi2wmBsNcXTvw0Ys/oqEFje3tbEsGNzEjobqDtshBi6G8eJYZsS5HVSA7eARXlXVkCZj/8WnFyufzH2RT5Fe0U+oMpA+cMeZV02q7H+JryzCyiB3uI9nGYG7W+ATh9oPu6FbVL4SDeO/F4AjzwFn8yPU0uOXtU1gPQTMAClZM/nPkedk2OfxKrz7OtZysOK7/+2r2lgkdY+OsSZtwvljC2xdy9B38ZtkWm6Ms2sYIs90OWLKiz2Y+vjc/vR2uh7HQgah+VWN9pOfCzbJBU6S4EFgxRZ7JeFt1qUnQF0BzB98H+rpDyfYiAJz3/gYyUUdkmMJbFAIOKcDXr689YvyyvwLZaLROeP7Uhw+XgIQlskl7wcQYgNDKBSVfLF6bHIOCcY0Hk/fSqcx9+ZmnF3qh4O3iXG3V7Z0IA+8vPCWgA7CHGsjmb/o8ajwo/LJzJy+75FBHr3uHLtLRSpw3/7prP9Eh+OasACfkRFXAROakbfKXc4eKej/ZQe2yzGj6ATjjbeRHIxYvP4niqdebvhW6qTpsGGTtSjy4gj0GIT+CBtqP02mEhaLRn8Dnpr2WRtDb72BbwDix7p6Rr5wZHKTjauJ4PnVCi9/LdZ7FNWjwxlYfPESA0jYt1suzQzktidLJrT6XJ/v0/xcm3eYZSAhXd6MW4kVf+ujgkcdoNU1ziVHB/wvwu6dk9Kkfj3Su74HSi84dGFAZrtDP4jO4312HXZbtO4OCoIdkN2VWFoRrY8LJ9BtGUZax32KREy/ODBD5ov6RGlsDJnsn8zi8UtNO/8DtIUSQhStJ8eK/owJrmmXA4HbhxoNp9FhLI9Q0wvbX173u4PvbeMR9G6UeBc6ZJ8UMicQfSTheQh2QOk6UD2wE4X8KoTKG1CJfk5r3lUx2HcJ+jfaAe4Ek8ajnSLn47uD+I31hJ6SPCI4W8zj4eNFrPRV8ZBkbuiHNDeczYZ6oXk7yA/H9DO9BdvmgjqkGs84bzo1XE6zRXWzpdb6g7xRZuWnxnuwg1xcKZhtJq8oQv8j7+j8LgCtZ6varowlAOUMzR3BIiq+Neaxz//LozAsYyqeKIAjNILLPUWFvqIs9fOcllAVVbTFvV3yuIdA3u8IvqQADJDSmnKaLut2ng4QoEBCBYW3THev/mSj9+ZBxyueQL7hszlwwBcn6H5MYCGJgwgSflWGbonl3O4NTt+kQEmR+59GMrYrpFcYsVW4yAUFgfCgPMMIHEHqMEoWDQgvDrZSt9YqFxcTeFAP0+nYZj8x/2rld7JgUAc8IC5ZB6JcbJqxfecGKjD4inqYmGxwI983zFJcfS8mg14+N+KVDX2gVSeoTvMwS8ifInGoPK3gRqK5TOPPE3YG805esRZ1p9OOPjveqJnK5V+T1tC80JvJyVG1Ig0w4a/x6RVUo+/O1DjDZUixkkzrHjh0lvc0Zv9GFsmHrIxPeV1ZD8+7aO8c8rG51WVKV9O99PfbsEANM5Upqd/1SVnwreNp70dWDlqHEhMDAxeIxW3F/b0RL/N0HJdfadtNYCA+lva9l15BptTit3y2zKmdyKDlAVGQi+LwL6IhTnqiEjiOgXgPamHYLzYPGuIL/UskgflqN8nzOxumTMgaJpmE/dvfkj6C6UYgUc3+DatmHXWn11hWApmH6GgnyW/VJRRAbcY3l5PjO0O2fj1WEd49SJi/NTYzP7sRwJqwdGfCqXeD0ot8wlqoGIF6Gmcbr8dKl0C6q/hou+tUGyvmzPRxyIHCvhs+Or8NrCheNc7+7K5onNW5swuMclJl+uCnfnP9oCjSRcY/8eHx/yhzBk/ht1K1Ee1mPzMRzLdX5qO0IfeadUEArAiEe9+VYSHikHUKHOjPL6khAQ9rxRst8bVTwHP2G/8uk+rUPTBI89pjr60lZwK5Y58qxV1H4ABtHpguTK7XCce/jr0i7sdaLEuFQPI5DLjOa8pzN/Uo10WC68bILjhv0KXa0BpWBzTKytnc4DTv7i2PED7cJtn3eRD7p1wt6yGZJmDwq6VaZgZtVEcaDyZptq+Hams2QDdpoLc2x3UKOF5sm0oMx8IZm0si6yPXJCGEBAaLAb35nnuufpTQhGbqxO/m8yszCmMI2B/En/+9WfGIsWE3w9g2nHpx7DGRwt9VKu+PztDEgwqvs36XRY+oc8ToZm0SfzXOUB1bu9LvDj+xFgzmToKQO45wv/OSspqcZRxh+QSJ+zsdmjp6/3flXtqj7H5wRJ9t0zRGZ2NpfCPEzfEDb0h0BOKrfyWO2lmt7zIKcY/yUTN1GOdDeIfMkFLpMVrbuA13nF57wvQpZGOmJ6+1cdZ11hsHQiKGDs9+CnuWZBIdme9h97QtCsslZBQFYY6MHRaws478q3oxTGAGrngYrRe6xPu66LfLx9pHt8UkM1SXZHMSynYC33SYpMFkOfrsvutp0s9usx+1jID6rJbDgaLWhZWKsX3S0S9kVFScTm8p+BT3mrIgfE05Itl11A30kz+a/uebBWwnhZienkY5kMpdlWwaZPZGDChLh6RbK73Zjo1gwJfVogfcHiBJQ/7Z9mPh8gLxjJGH04YjSekqYw+IngVkptt92aC1O2qgFDp0KHndXl2R8lcXW07nTjss0fU7Eyq8V7N3ozHgolcKb/z94VRROiiXq1VuXuWaBWl04l2ENyLGwPI4UYPKWvpD+T0SKc6f9twg2Or2kG3UAXbWYbizGdPBc/42NC0qobs0M24Nzfs4JE1XYcW6NlJo7cuLqlVcfb7+cgsPGa7IYAMbdfOWAKwP33Y/uJ0DJTDca+lviz+ESAarcCQQ0obHwlaPoqOuiy61/orp1nee8xKSJ/xOSDCfe9jSaNbKWIQq+/IlUQJU8V8HtkXfNElkpYggB8G8IVQxwZuc031QBI9CWf1bNhmqBADQwOaaWI939EEyhOB6y6gA2Fobx9O/A7p1NBFwokhETPEpvu9DquZuymHj2efG3m/1KPK3S8wUNynkDoPCW69pheI8Ch15KX1j5D0tD9FccI9vTH01zqUsvoKRsUf24669eg/IOzKYwfk10QY7wqbvhHOONFYIDdZ7nS/mVJWQ8KbmsEWQkkgpocNuHNT3/ceSP7S9L/uXfT/gMiEnxfmEjgLfurO3l1dnZNhGzHwZLkQCKDm7X97J6ptpn+kh3NZroCeA92nixUCL4eXPqMeK8ybVrLhIkRP7x/utw8VzeQSp+/3l5KUKBgJ4ZA/ojXGAJqVt3tDy5SWvsXnAlHP/5RTqoznfUCE/PSb2GGqoBCUBi/p7ZyRju0oUIFt5sAr37A0U/fMhyguWJ2HWAm+HTchOVP132UWRbfSzyPEweRUId9mChPGgOHjZZQHLtA1VQRBeD6ZM6UakjNGazPZonDbPz+BwvloVXmJVznlOZ/Q7NFrA16JJtrAzw4GnMjHVM3RUXkL7QU5tn7QVLb65ou1yhcKnqjkh0LGXVi3jqi33+m8Zo+6Dmy+6r2TWaqBIP0oovUm50lFwAUeur9yebQKdrMeNbl8/nvmggHAfzsaD5TOc+22EOdX3y+UNKC/FlR7Hz038vJNlw79+CXkstkqoehKWMd1FE061M2V9gDBsGTw++jljivqfFHDkfTIIlht0q9tf1mDeubb6pdWSg+wcGlOzWTOn7po2wmnDXu+z0AW8qvnHANylWUf3J2Law8wAPHtl+EXWpBxKO6vnRqpZJ+Lf6U9VzROVud34evsBmUsuDUSSvt7nAyKsVMkv83e8rgOCORZee6wSjh2ViIVvd1LOkSaopVZ1rk5G81MOqdbrf7dyK0/tvRwFHTyPotmN/wE9tLae8maGwFYC7Jy3zIUua6kmqocy42iUYVy+WsdmCZvLLQmjb+c+epI1HvjXLf4YFaIdOjH1wzNpt2tc/d0ezMZ3644WIDkt/QG9k7+FZNBAFpHd4Hmg7hVdCJz+/MokOzPn08kOMkQVQ7O7UtSgVyOORyyDL3d/RfON3Qp2zJ7GslM4RIXmgoPLKcAQGGYOyP56ozn6WHu3vw3CcY37JsBxaYgjfuZ5wNH8HxvGvKpnFqOWrkGhi23HYfBdjNDezPpJHiuZkQ+TZXNQWrQgSd60Tp8u47lOvELlWn3bSkElRSt6MM3+tuuBAOYfw28QOCDV83WFO4TI5XGxbuy96Weg4i6noswzb6QYLWMLfI3YTAzoHT2mIdEO3Oe1zt8Auu3326AD0tvZzj814Pl9n4qPm6U2NiCIPGakEXVRon9c3t6FOWJJW98mcAttz/BgqA+xycn8NcxO73WVnuPjLAjeucvimOE0SfJZFxMkSMg8xBczrPIcORRAo8qWxFCnfOu5GsGxyplDude9DQkk2v/TAXvtZR1ou8oZa3rm4vbfIzvaK/DSEExQ7rhKpMuoCn9pXfoC/qu9vQMdGIA90uzNvG+t2u4ky1loEvSEo2ijqLyeeTgXoVNyvb6vj3oABbpwARxv2OwkexL210/LSnqSosaCJT6+eacHOUwfqunAjpw3oKim4dP7m1KZ/uOue1VvUUE6cVPOICIw1LkkOz1L3fI5Y9nlwSN6MRl2Wx9WQi3Wq2K77msiZEO5MEH+8PSiEqLpfA6yAf/v0l8N8YNiCqFFQSn8CcMYECk/ZRCHc3cyuS86d1/Fykhxf99WfZgm6BIQDzGBFzZIpI/DpxZ9O/YqDi7+voeA6ieoLDTO1GlgF5Xtw/qwe5URJufq7N47ISsXQ2BbGmwhrPM5TsNwjbp/yPygDFqBEFUqlkd1C5qHlB9djfjLwhx9AAHWj9qP/lQeK9DLs5ZEJnQ4Ohz9VUeAqwAKamF24DsaUrgnC8vZEJfnjODGrcrOyuWu/42wxpP6C8wgOCXhLo7p6WRKdzQPXeivvsKiiLlXAdBJAo6rIHUHXcB3XSaoz9MIkTglvGRfzIlwqOtAUyD1ZWuK9xZUOgysNxLsI326zYPc7cdYsABbQ7UES/3l0MqWYorY2fzIok7BvDAKSS1EM7RzZJKyauQaeBRBioqBi9LrSbtXtsVRKy/O1Wo5i5JC1Gs5K064+wietL0OL3lLAhye+1weLnyqsMvwsarY2P4/V/QEffp5PmKlYhcz0iA8TpEfVsEmElKL2z2gzG4XR0DqMDFAGQEeu6+fRn/006twDS1Rt4Pe/8ERKS+k7b19C8nnFShKLfDnUopj/HQDPVINznsGQbwbUR1xDtRHnU6lUh7l4A/lv3fY+PGoxW6E12i1gPBvdvPN6+1ElkwAJoCraWsxsIn0LY0uWm4+3Q8qRAfsGX8hL9fiYsOUfysYEwBh98mZjwCYOjR1pnm6qDykfdj/5I6/3eTFm2ZclyJve+wsL5dVSH3q4IILSkH0DYD/yHxcu5Iv6yQO8kxvaliN2XEpYWGizAsd1W8NziKj//ddsw4gD81N+bmP86AwbIfM8dQKIl+BITUpuTnH0n1EOqHcIYPnS4eBnQzehAgDuxRZNN7VLohda5My7HujmRLjAs6uMinFLjUIyxkBjx73URE+vGXQ6JrPsa9mVM/kEWejVT4omivsZL9b79i/kEprUmbY4fkCbu+ZhLeGbufN5F01TPC+VPy+NeGAPLCqA7QEl3x074htd8CAz+IKWEbWQl9Lc0+n2x79dif7vhI4IL//XpXd01Pm7RKfFnI6Pz2u3BM/0ZJwbt23V2Qlp5z7R3Xk71QGUKsQpmvLaC20YSHHJZkr8m6NLIVZo6LyB7WRmrwxv2UxmN65N/kPHdA5f/iFgMgLBdej2b99+HLKy9tSikk+1R+fvfCYUNkE7XCKvdk1mNXw13B3xaV+XyKqN7hKaDWJDqxzHzuW4mgp0M4w3ZPgG1xubIJ/v3GY6dNnBqloHyUP4ojO3p7eeSXPkP40hvoSLkMF2zQ32k6a4g8IHHj9ACbOWGmHU+PfzNvYwBtP0kZA5ghxDbqtYPBpibY8bHCcD+pHgAHCUjdUNkKF+SQiKX1PYl3RVeq1eNOzfhjB1CNrpb2uRz9M6wJFji8udMTuo5Te4C0D7o40Ptd4UVQ0ozaI0OpyqOyZc1Th2g8NdyEwLXQ6QQHzgN9ac8D+YxADbfJZfSYBVJ7ragt5MrcH76coOKp+mCsoqjzdu/T1FOVcLH2ZfqmkdowBJyk00t/I4a18dgLuvD2iUpYxFltM6tFhjPLyiV8unHIR1jzIrg2RPN33zNWNzV1iSeSiZzLVY/TNuhgh6XGV0sXi0rWQUTBYroCjL/0PuWuopbgZ/w9zb5yL3dovunIcE00ZjRYaPCtXiz/blLa6tV95qI3FKW2cTMZhAFAywMJvtmcC34YaaHRwQBaOLrGrpXKp1uV/95nMNuZN3ZEtZk2zqpLgyiSov+QUh+OmP388l5Th0Nv3pAZxJuhMx9a+18pPuOmMT7WI92g+MX2x0d3VzVQ6NdRmq44Td2Gb/3wTEW++hDzIkqNg61cYyU0scKLhvOtwAtlJwygtDrM/Vb7qeDXgKA6q2645NumS82YCtDcR1BPNsuWw1QWF93SYlgJ9zowSiFwMnhkHNbxVM7+ndgExFAJ11K7sTHKk3pwLxTJS6iFp4kKMDMGr/xzqLgm5I10lpwcZluKeqNWVUzzJMcNdFTAXnZDNLywk6aoXhZtdDcpe64jxdhsIaWpDJTCfeuYPRHE4u+x62o8/xrESBh1ww21+BdSUMzcv3XsuVWfiC/9eu09rif4Tx4jWqfUfu1I6QDfwsgOgqxttoShGLSggzO+9rm7bVTGQ/y6cQ0r2qirAXBLoAZ3BP+ASnliKNvJ2wVT9d4tPeSF1sjTo8qcIEgf1i5jQ53XxD6YXabaNl2Z/GMdQT72B/0UaC/cfcLaPlq2VvfD21s2Ciz5DOUoeNBjR/LCyHL83FBxARR3g3QkOumiCFuw3vGmThQm2TANpo8l+sZ9olhT7ahA+LVu0mWn1kE/xJbU0CidjNI2gxyuY5aCTuxq7e5qD5EHnUjaVw0xipxv+fVt3NjaM+yzIZRae1Ez55lV7V/ol6viR5YQsGDPbmGzBfCAY7PdE75q0HIjsrHi5W/cLPVSCrdGMZ/kf/fP1XTM5h/tVVb7nKxLULxkfdPAfVT3OseVsicq3Zmdn+zvBfMSiiP64sHui+dWkuA/kokZxWxBqu2pZY79oOfKmz7A08zFSHDOwsaowqQQpEL+Yf8KGi3gHjgZiGLLPw9mp6GBWrY16DXNA2kcHlyQvN51/0sHOUhzuF3QdDRjiyOe4Q6NP0GtjDcu3eLuXBcybokSheSGyVGHHhDvDzVdBaZas4zEqmfbPMykKfR/hXvEZ7tUDWLQ71kFbjAsOLPMx7i3YNMBCBUwzZFsxSLEOfxnpOt1NbIhWxrcFltje7Bn9PpP0o+N/pR5RcI9Ws2n1yzfK0WNwkDn4yA4w73WtFnK0fyKHKmmZ1wdBlCp8U8j9I98rumuoW7xg+hnOY0bHrIcpaXBzzb1GIr9JNdn8B72kQF9OEKbwKu8HvIHlyU+MzeCmuERmpAZbKI6mJF33gjMo5T1fcS3FVgxumJ2RpphrYk/smz2s+F4s6IW/KWzN25h2DyNJUIDA3i7GLSiMRfeiGJXDkx1zjfIjskLiPYlKDzTs+W1F0WaKvWoU7b89PNyvdYH8xgnlcKMd8fJySOn5zAAwyU97Ptt5fAfEa6mdc/6yv4bUROWbseXFkwxUuCd9GK7hb2lkMRiochyInwa+kHQ1vcdcCft4/uMmUzYl2TaM2WDJl/iCC4H35Nisz4PrX6Zz7Ghmb9mdQS3yAItI9PkEFEQJRkjyFLj8RXO3XNtOio+Wq/d/gAKuQdGOAW457BeauxBSN2IHfF1/xil5z97p9FgPeDsfS+MWIly4mp10XaJAh1lLjpx9DGkDyfkt2gZCx89wiaM/vL8rEpIsvyk1M1nDCBMj3f/23p75a3V1BujupBYRQwAvPHfDTadeg0uSRdQWBUQldZSeWgIB52xTIJOOgrSVbWBdzhm4FXu//50z96SL4tSI8YAuJKht2v/3Ssrl0fsVYsdEm1vMICISgbBNGgwBQILQOq3Wqr1ua1epWcYgMsRmqQivB9ijnAAj2TlYAAhWGwhlV+wBJ4fFIFXvmAA3XoQfyEM4BKvHQP464u1RpPkVU+rIgKE+aWxCH3g0/ZfrXWn9wv/rZYMquVEwAMk6+FIR7hBxUx5+SkGUM+rFTLmgXtf2oEBOMHy1Dp6safoOSe5Yr9yZIVeSoM0zEVXuknWj5iKXC/kTJqG8IBuNVA5XjxDo9jGqmgSEx+kbB8KrHKt3jAHHjGQRzW332pSIkB3hxjADfY8/7X47c+YbP0ZqYDD0PPNppJTPqCTKrnMsL6dW3CHxI99QWF41sr/tky/RgDvbl0R5xjAmikI1eqXB3RuxNlf2VAVPeqgWlYBr6rq+b2IzYJfL4DubkE321h0htRjB9cIHC0djwH8rKSk2MQALu6EUNeTYOdB8NaxFgaA46AXbr5pW025wIcBcDOgUSAMgFjB1ekvBgCJxXboyn8NqdBzKZd/0tH3DjrTLm8SW5rwDo/km2ZFgJcQc6Frk4pn9//dtqHgWg7aqcFO4qRKBtErRDACMX3fPAGudw00WQavqMo3YxtcYQD4AScL5QTIuhgUrYPrdVgh8jIZG9b5lniEIaJu6GaSb0ItP2jxbmbzfltJD+IKRwPuQJV7WX+8Kd+5b2NBOIQiwWzuJhUDIDNs8VsyEdJpkUSYpu+o+Z9XtJ9gIxn2BmLhATpAU10zFM0WjcwD0UgBeVSludqjcfS7jbuZWP8a34Ym1zJsdNrbJN5WgE8GwP+1Oeeb2po+/EgluU39xoMLLFjhqnWmJMfIusfUoVlVpnrepe7jcntJ2vU75aHh8CaBHyWwP/di1PydFxb8lTAAJZHkD8I9XZngHph6mqAIohHth67Dd1CA4EvoIfHok9ZxvuNO8K/KZ9xKuM2iQPnyy4lSF3wrLqxELDgMyzBZf0Z9C9VzkdVA3/tgB+FpRUaFNdXzpn/ZB2l1tVHTutFk9ZJjbqLvLmmWs1qD2eMa9SlsItONCJYHO2/iUaPy2ZdmUyVT3zOSdgaD+kCqh40vDvPq9Ovqoue5uQTEM6qO4ZNpY7U1cVttUg+5l61Gn4/J1rBN7tbTRwu+zXmi7HVT/kuV7hXHMg/5HpHvfVoaWW6NNB2559SIFpoEnux+YtTzjEzIU2qpzP3Hmk60wG7peKmiVxeNZ1qZflbC0rfpZEK6lAbjCWVi6X9zVLaz3uXKquQ7xkOsn30oPVYqSROVRgsqWayUvGx15p/2d9L0xBQWd1wKTBR8KexqLrjYhvt6lN5xk8poTIpzFzbMbUawUQV1c1otgl9j4c4dFcI5z+N0hB6O08uI4zHJg6A+jeX8t1BIoVwf20NuXs2AR1HpoJhSzg08ilnu2ctV4JIGz92nSaLba987IlZC9RuYD3buu5LrIN8hZpOIIm4Lb4gkamPr5wgT7gkjXOOCOegxgB4PZcndo9yUL1/ouLBo+tfD4WmLhRvlzfQr0ZvzpQR0E+mU2h9343m+pHxG2KSgUEu88hYwoD+9O2kLUF8H5glH1jFsgd5PRxGbzfkLT34ggrvTTNkPWL6+MsFmSHYWU8IFDelfSfcUvL/Dk/Gib4+0Gac5id0uCKhHbQX4/ELV61Mlx4iVxlC7MGuePgzg4dMyDmKt6aOKTGQjl64gFvRD/LWBcV8dgWX1l7qCfn7djozKgg0XQPo3uIjhWRR75Hz+ZNPgQnDexp2u51B7dRjVSy0h2ybYvuKxPL3R65epjJvxB8rb1HlkQKUygknNHVRJOiQhHdw0xHxIU/eGpj2Ra/9VmWq73cgmh+OHKYpnn5cuBYaTdyT2Rvs1vTo6hsQSqckvp7KKuJhqoQwo5nkRvyuGtN0N5348v5UwgRqJ+tQHZH70dik7J0GLYNGrBZaV51AHdc/x6N4GWRJN8o6DNKlEsvUWX+0xmgnNCMVX/oq8NWvhS0vxZvJL8z9fXVbynvlEbhnD/JH2Ap4K2m6zZ61W2t9vuvh4WTsaLfEDLrRA/U9HApy3YKOmSXG8xGI60SIgdOWOkj5BC69Q0OTSiGRDl7Q6//DmdV47v68AswKBlqKcPexCqtuS9JkErlm+wYTXQKau3rNqYUuG4TTXpteBVB6DgbSb91+UYXseB0KVZJ54+Y0XLhU+m9LtUxCLgyGvN3oOxXiZUe2x9gSvT3FucH2tkGpLiuiUgjKTBJ3lzaSvA/JkExtWPGsVBeSp8EKYI7o3P14vi3bvZRh5D6PdraXEC28M4HM0B5fBaUCojnXCbxGnwIDxkOvNprritw0uQwm0tu0BEFdA/xF6t0inCywGTLm8QrKz2V7g++9MXsjGCrlq9t4tEOYCxKApE4bWu6VN4cFT+oMLgquWaUaS36NeOejz8qCfS296q49n99+vR20CExcuCgc5iH+++ROhY67e3/6jKGhmXz/2RKnhZdFH70K33zcxX040+I737WFVIuLB9lFvlW/y31/xp1N8+Lz9NXi/qaXWtOEpiML1OjEFO/D27Un7Ea/lPIdAzEWZuiPowOcyJXM7KL/sIEiVX9pHvz1tuTy7AGNOpQa3hqVU9Q0pj+qRNTmSe21lWlC3Op7Ch1LG2EiGmLZMWQUu3hD3BlQ2O/4lPp5YRPdtBfO3sph6ajWdhOl5R3eThMCqevos7VV8nZ9rf0925aebrG1kzoGd04WKMlQVOBsx4HxDZ87HM5r1xYWLdr7pJgRxcltwdpJLjkOwkqzbPrnb+xNDIuO316Zaub0kO7gl9xjAfSnes5qmd/GIAkT4vfaxfR438YHidPxy8q16ARvRt8/ODZHedw7LmYXUVgZ1Ew2kEdKmlq0+3MzFCxlGPaJnJgRfe4J0staHpUEC2TSRlxzKCk5HSS/048gSzOlfPk/hxJnPYlfpmmddUH5faPlh4UROYm+pqJuDlvw2jWdXfUcdRqth/srlynU4Jgl9EeLV1M0/8fvZ/z5+a7hJvyjUkI3BGwD7t4uqBauKkWj+xmNYHHe+LhzX+v1yXgJ3S677EsWGKsZ7/SBdb+E8z7xwTMrYZQy7E7uhB+5PJQsvYHetRhf5sPuPDy6wv3JSItOMOLobXx2Tejbi6zocDW5ZyeRko/IqNCf7u3EitPNx0UjG94WMJ9EI8UvSeCgGoBeQMe6T2+EDYZ7mbz+MUgt8NzjW8z4qvZSO/EmRyzwlcElgxu+Y9k9ibXYwwpxg9QgtAI89b6iGbkkLqPivQaYzmn2DBpoXcpB75TdRrH81jRKpYsQQIQIKnD6mBp3o7f7FDxdcFLqeDKQnw4AXlweGPvV7jgQJGfEDxJPQgFD1Gh65cQXcTLrHI4UNa0aCScyrRx1PRbOuqlUPbTUd14wIpX+cs7/u2Yi0Ypx5nxlb5vivEiei8nFiaxUzGRqsKyJgLqfusPvNWGPwisEpXj5R62lfrIZGlszYKxeWUxL/McY2LfM/57fm0gTXENdsAd7Sp82C9hRacX+kGUVWdYre0uhwf66CtDIgS+oSuX+UrboudTBm+3rWUgy0nT1eOiFTmPSalzyZkOBgr5sff1JbBPevqXuTppYITH070IzYORFClM7c6TLnbPiKJas3EHKBp9UvhLZG9WiG1fTrFfflWS5KPNSBwh/hqPpVvRe5sLvCUjFdph7x2qnY8sCKJVMePlMFOCpp79arLDnT/UszVPfgY+1xJzkgkFPqnP2r4jwuY9oYE2nOCJuSy4mmJ/d4mvWVQ9ef6bFn+vIp4JYAXe2ZGz5oli4890zb2E6oaUoR/NIsRBt3qaT0QDcUwgd6n7Z1cXA/Fj/BT8FOuO/lXGlEsBqDJoGexr3HAMTNzoEbxms0tQn92uZekPUPbriJzPOu10vNHv/eX5GOPDfEPcz2+lk83yucgIOeljUwSPzLPlehlBHXIs/eHZJQJpP9h9otYWJqQE/CueRPTA1e53Rdbuonk9053PFQci33xUZFHEbNN908NhuPbLLKWnEPVIkt+LIScM6rNmMVeDNsYo1+iiFrRxkDgF/oApvhsUxhj0B8uPH24hjA0xPTi4KXRtwyZoK37CoOsTSS7VHB1Hn1B/wM4999ZT7Zj8mSRDDEWDv+OjMWK19gaCj3iaNiq+Do9nzgyKzHMBNhp3KaaSLeDDeOKgnAT3x/B7dIG5u2JjJWrH3wlS9iMP5OM7Zbb53+CjbCcqCkyk9DMA1LIGEUeuP7cW7+g3VTY6zlT9wzHvHgx3RXl6XLwASjIcH8OGrSvAaJcz8bZBRvnvPcqCllMPMcP4cIkXKg7ZK76KmLDZr53rZwvDo/ZXOnwXjS1a0qj5XMCmk2XjwguJERzPpJxGQxzugr/MQ8QJvZiQuAs5zHGD/CHO9M99xIfIf/29l4ZmTAWEPra7LBMWhAyDyP1EskHv4AxbHP0zbYGH+fK2HsrYZx3dFlchwR/NmcXRWMrYlihmKRMI5ehiEgKzGTq8aX+3kHbm4ELLYmhsS79Pd82FG8yl4Ua+7DGy2qloqQgi9ORhXq07UbdSMa3apb3WTD77ObGa3Lf4I6NV8QaOileeFuaakI4SIjnui+fpjFvyWxry6C2r0Y8bB7ESMIXXiY4oRFKjzjNyAhUFHxh/2ACMDQeT7kWJEehaeSPDN6Q0QgRyYAdvLADz342NomQkb/i2j8U4yjO88Cb8qIynW5wpYiCanTpp4YI90tfe53x1+4zIL9N1qj47yJTKP7YWQlPnpjS/Dz040Ttn32VRF+qnNdH6s170el7rsOrUeNabyZlCXAgJjIy4P3bmMYQG3tBJOE0rRnajna6USNTOf7mtGeNk4wVGMEWZN+N/0VMEOYx7XFPme8wRKNAWQ+bj3mBV0pLmyVYwCP68WNXqGvyvLugHvGm8kaZYOxstUC5tl8x6BMVz/Vf35tXV7LcYVoYfC/L5I7RZGWyfwdR2rFPNRZ9vap+UMATnLYEHk2IE2Jr5s8+1Fu5Nj85+d45Ntxn/EnNRSlXrw/kGUCUBez9uZ+xlGUZbZ7YM86xGwHYI7nh41/fJDGCst+PCQsIJ9maC6cMYHHScf/oNsPa4eFhgT3WGGdG3L/ZivBK+tjKgbam26/OoIig2ZoJE8liuSqdh+d8u3y6dYegCUR24iY4BPs9gfgKC3fT5Qx1vfciJVOkye/7GJ7SC/qBZY4MADQcLGd1phZU6mVzQxRGFxtarRMmp+wcAlYri2DyjSP7HQegg+/wpfPReuMp+uXO699XyMzUSA9fo4BDJCiV2+uyq1/hDFVlPWQ2eu4zDMwWbA8Cq29lKyzfmvcc6HK+nVeYHH4iZoEeA44nB+95nqcbjfnTMCSgde0Bh5pdV9mPKO6/1Zp/yj9baeFBjiSYN31tCIgpWnyhq7Qs4DMwStZfAnxRgD8agHeNiOvGeu0wARnWrkoI69kafzpPFomeND7U5j8eGgR6mkw4k7hfvMD7W2qnBzrc32ZT+H+ob8sf2vT1PGXX9veMpgPTaqrvHR0DpAYYS4hPlBQw23V7TJOUjS432odkjNMz8zNbmpU9ouM9qNutaPQm+XiilvmY4z6gjzIamlP2qvPKLPKJTjQWDLu8+baRgKOPvjcgYQ22WDeWgV5bZu0r8WfpzqnoDYgDvUx13u6Vg0j6oMRPvys5SX4XSiH9y6gxrqCpEXCDBQbWvrBDc8Vv/7LDgDoH4gdr/p4Sw99V676c8F1S4GUb3ilH8pq3Oeo8GPvjiKsLOVlKXhFp3asFPyUf/pL8MRK+esXGYies9N+WcEGmpWtwwHtT1W4kmZ4qAmlvxrFRy7L0+8jE4/ZmaW/fSfjn5eauhG1szWIEc3CU6JoOqDMe7Sgjwwvdy1+LCd54oCv2JkYl7z4WI7S3jWAT6Oq4Ie86hpbpG9Vr9oTN449IP7iM6d4XHG9oTbgxKd4mcZpzh08pqi/ike9uIS/17BlAvKvFf73/kdjrVqglq0T8E80OkJWhESTNd9fOFpQYIeGtfHiaDt2x8iP+ESVZclsX/13RaHR5EO2x7/FZqC3YZxB8vZM4fNBTQQ8jy1icBEi28XPshyDA638+fssqAqEUzhUOajPd9rG/kULAzO1wSHIiQovar0PWf4VdMSGkDtXIqJQ1PHBLdrb5FjTmOQDDipJ4O16Uesq43MbP6S9eEcaAWgYZvK0wvpTWGrAJc7kdPU/ziO6MPAXd7RAPETweo5Ahnnjkgqr6nOJ7aJ2LHURRxqE8REJadZcMDpANxefonLaEzLYMGv26DuWUY0sXj+SjOgrvY9Nr68HsUb6gKOZ7L57L8uViaC31VGApPkx1TiRfpJ4vF65Od0Lwjj7zLGoxJ/Oq/MAnKyrEOGpN5yKRKQm8AJ28gIJXCVrgqSNSG5Sg3yW4iG5E7jFlUDIjDInxaKpwvT0IS+U61MCuBpUvP7VqOo9NIvgduq21lnOrgtq7bchwZia9A58kqfbXktXdffWQp8SsbGT2r4qX7hmGOAaFqS8TmUsYzlAfHH9qwYC3waN5/fRcdlWxfBbgqYdRAPAC5ZYAn6avXsWuaFdBdLcB11SXL4w+3ajGupfeTRyulDgcINkV9bonTnpuGJLgzj8uhYg4EH/bbdecok14Ta79P8Qjr47uNcN7Gbk0hhLhGu710L+zhSbBDG3m2UNGDY0uiqn1O+gH4nq0uTl3f5SUOfQm6AJ1BhLDbo9O1zxBz93gBlwEUfvrutKF1aqodj9dtBXdsqFhksFCHoGK3giw5Z6dd/B4eK0cawiTq0HAwf3Y33ziDGxn4q8nfR/Nmkcaqt2aKMTNhOK4Q4pX7Cezm5tPDiYFFdWRUU4MYqg2ON00dxeslbDAPItFT5vGUXwz6H7/DcbFmPOsuBVxXb9MP/YMZyPvW7LU1z+OGlRd6ZsVOUkJ5Pp6jwhl6ppdQ/e0Ci79Bx7avRdyO36L9aZqTiV9MBptKLtq6ergGJJxJ9e9WMA/fW1It9o6MdtWZ5z6RjtrnCjh/THB8kL5GM9G4vE/kyeiZW3aHITcc1oglpEcuKuJWpiO/bZPD92eiTHyHoTDnrSxqrPINdhQ4oxq/aeKkNcwXavjiZtUtP4pPCZIyc8pfgBh2OqQ+T8gH2VcZvI0YfjmhppAE27kVZme9YHHqxDTCQAm3h+zecAQyU2VgC/pobUizSlZ9jikcef0NqErSH8aWx4PFTy0emiCRxLzgkhLj1NbxDlJtxRTBcCTdo0DNqQM434+3jjrvJ6Psi/b654YwItIc7jZ+ddIEGBGTvBFftmBfVXGEBZAvS4UhipxpH+O9zJQX3ZNSXeRCdH2QTfFiuCDR5PJ+9pNyf+GH2rZNNvdS7Oc/BwaHhPTTfQSexlhXxxh4Sj5mtKHWaATLlNcfsHBGyHijtQhx3GhLcGFnCTttwSgc24lvGqu0Xz+gACpZ6P28l8AlGm+ud5WvpThuOj9qcjKf3oq9BP/fC9WXwe44wa/m/3ARM78YNwKpops0KBj1+jezyLtjvtr2AiJIdQJXvaqRih4nzm6MziwiYYD/W/r4Nujz19Z5z93T+DfSR3y/FMdxxeeIP4gk/ybWVocKdL4KqsBp7vIvAaR5gr4M9WHyjjNdlQuR/obfzU8BzVYbAUXp33kNs40LLW3jy3j6Ldy3J4kpzByfP65WxfkQr6yvhJ7OmXTddr3QxLdgV72qjWB1xgpieJf8GZytuQIG39j/5JlqDZH2Dd7DL/tWNcxBg3BkAq+283eQjJFjTRw07lAfILR/9hU9/p5mCMrdiWfoNY3Qzx8qSbu3zronsgQ2t9dSmgTcQzXii/XrIXp9dYv/xuJbDmeX+c4M/+BjPDXT9vuFKht1NFI+jLZbFdHtVVeRTvZh8wYa7/suy7ZpnOn5ti5/x3g5UL4pPxwhcMeQKUV8KFX8nfU+/FeRVEf/BuI0/C4/4nuoSceVeWvPY2+1u9QbSHfmXhEPJgNARowksiH0N8iOfXmo8U9OXp9KkWaP17N1n5YiEAumPasLrb1uf18ytxFCTjO02dUaaGjyLNistCnpasvOVCtqmnrGLOlin35KfvImTmNFlXZmvXlU5p5wb+ewymcuV1w0eFVJ8lPOEYQEl9kFEeqmBZdmFSLyE8XbqdWQDYHSNfaTgtpj98bdu2cFDf0N0ye+aCSGCDZOYVu6rc68UFmZ0KFIQ7E/zk1x+nNGDUryjfIJPlvPmkgWTIhRaVNRMQr0j5wIPpC8jYRYhe0rgJ4ejUYQCExkOrS6a9KWkcCervVo9tDEgTUIcvza9PPk7GCP8zwacR6bw60CVtpD5gX4xbXjEckzv6ODY8lXIrMika3PtzZBJyWq4ngixln90+B1tr3KeN2awGsxFKdLHwT7znT+3tfhSeT8dog53D8VLwcY278Ye8nmkArcmAKcpfrkcic9SpFpCKf7xGE2n1587SO7mRFxoLzG9l/gia8UqSfbJd2NN77GOv6ugpeqEc8U8gOAoxTBz4VX6GZMHvlO+Lop9l3OUdXT0+rz/j/WTqbKZdYKaC4qf+o5JIz25ROabGUsFXHMTurEskJu1tS+FXMLw5YoMFpmqmoX4OJbndXJdfECxmIfcDxVTlu0RzFwwYhtzZ7mDi5gHQ43LpqkUHvT5nlwLF7RgurOQcXVZ6n0LDjoLECt4SAmbwcdSFfEBmSsOa9Z2FqgO6NrfYcKbn0KvzO/oHLxvg9heiYlGOtfpCwRtpaaxNPRzSlO5RgzwGhohMQ05CRU796Ffr0GvNliOB/K9PXscThGagvZVSxXsHHMEOkfAwDiRLkXjorW5Drxw5e8sYKwagyys27kYRu9PGdAu2LblLNrR/7Tu7+SBlCwPw00t2eE3UyTe7H1NLDB/rZSy6wr1NvtMb4/radEJya7PQJShmdOMbGzXan7cNRLk6uLsw67CxOTRI+jY2xE1rUf3q3Yn+FhCqSGlFtmfUcE0kzzit95Ro+8lC9EIraElgJLaq7VgC4rAktm9BbuahqOWRoaO4QcRCJeTQiK9XqVSBpCC3mUqEzzszJDeRuZarBOjaxCCss14iyxHdaLk6gnKGaJgz/bMneJp1AAdiut2DDJ29AF1/SdN8YgzAXyG346H/avSb6E1aOqOXPEjmyqIekSG5v6KJLt88VRveNoV1LGbgoNYUaIqOkYQllQleP6EvmwI9AqPL2sM1bmcsJqKzpjZfDWz1R0eP/fn9f7V9dVAc0dflEEKwkAnBCTAhkGCBoMGZQPAEdw9uwYPLQBLc3SW4u3sgSAjuzuDuDAPDyJKt3aqt+mp/9dVW7R+3q6v61ev3+r537jndXfeaO3qqCqPJ9tPIq1sbSssDTFsNqWRW4lEFsLECci6LmEN52YL9fpYi3h/spKsuMryAehIFwT7s2PfBlrMRd5N0CcDZgPA04UmT+PtwIy/PjOVyKu1xKCcFoILnZHsprlgL3scTdn5eS1I8/UmLmDRmLIVXVLD8QqyPcnJ/9uNlcUZorSUEj2+n7d4wy9f/aYYQbEfvq8d/BjcQvfz9c96ytgoeXWBhaNv4zvZyKGztaqIGA4iKiNcvrNtoaiGiTXVqC0pMtsaekHHoT49sYmVFpGa9SDWfZVJPH1F3phafSL8JQXog2UAO2S40+rB74VJovXBXmsc+T+Abhu1EzyQsozIejwHMksbWTrg8J9/T9sdl98dt+HKg+kZNxppqOan4JaJLC5wN8i9dFJA9MTwQT2gIGfm+EkwA5matqwu4fGYQasHUImqtezQqxBa7PKgnHD3UVaGR2OUMOPC6U09+TMgKP7Epr4o9EiDFC116u4Yd8H53/9MoUB6fLgGQ/2R6ajaBkyk24Fic8Du8mHI5LXJF42MTgMDbtVQoo4dN+j2WtZiyy9RqqqOWG1dqZF+v/NpvDzJnvI/8DVrfRLJw5WeC2MNEvdLy3Z5Jh4UfiVrHDbEYtO3yqdewdzPG++Nw4vrEKfr6H1ixUrxWuoPSYMHA4+rVH3inXnW0itQNLmkoOyvlXCHmCjy8u91aHZKdyt64a2VqAm8t8e8lY6S5am7QZoR+Zmzvvh/1LGwGA/hQz2aHAYiaoaYZkLbFDTfGz6TQ2WV1nPchXdOKE0xiGFR8AcC/1TrJgb4dV/9jNya/lejZUS/EIM3mq0jv99zDxX7WTmqsKiMPoeEdHSTEVoXgO74iQs9rgYY6SHWETfE89/skr+cBiS/8NERgwol/FK5EvivfeJYtlHiz5HWKI9kuulAXSuBMF1BnXepmjJwd99mBuNGIgi9g/DKrp5avCzh/GEN5svH7L7r0690epPi6LNC9PiQRp12J1Bn4SoLfGXcI8mS623PAK2sDWKMgwn02PqhGCZ1+k816ecW3QDG/Y1dkIcb/6zhA9RmjofeM4++o+jNHW0kc4UNIsscBG7iJrHmPRlOkZFu2++pYdUgalWH/Jk4Oj0BaIwWqWkMUWdG2opGO0CCiU2Z0mvC/1ZtsMNSh8jTxK4wTtIgzE0qwWdRXqvtr67bpeZuqZFRkcwUJRqS0TrKbWQrnxP8xRURP3WqlGA7qLkpZMHkMvG7NDoY7mJsypxwHbTh2Nyklyo4dqje8C2/XGCvhDfX5qy6IGzWtyfTj7Y9rlj/7UmzU1IuRYWMkRC1VHOdKQZI9H7YTT9vCrrWUe2oaRPk4TFnVXQ4lTGx2h+EIg5mE9OS3+9pzZ0arEjUPhbFu40Vtl2FVj1O3hAHI0obob8MRhCUCMKqKt64lNOVnxfXhUHGrVwN3heUNicNslx9eiKUT+dI6QENkDfbwaBtn/rRTYVc+YEayCb9wbLlAKp6tNHusEBa/4I7NINGSXKhynu6k1tOXf+WRuOB3IiO/89aPqtpHhm7SO8AfTKBAzKolMjWM28FxIjRn6XK2s/P69vVmo2n5HxFgMctACgTvXoBctehk11qC21UdyNo7Cadx4dGouhIMYP3hDJX6j5XYLIHcYb8/GaOnXh9eRjVXHEbjHMQCYZ+Ak9UO7aIlEhUxMuMqxqVvikT6t/va9ZPufrs0eMdrkTvZV+og15JBgv2A43pfNk459oSXVMfumzcJ0OwqMhr3DZOJcnwSThF4BYkcdTEv4weOsaz6/ec5BRqLzcWr+VM/iR9e7YpolvceVQ8ARPrb71oO0b6lmd8cOkPoJDJ3z3bKFbcz4sfO01J5BG0mRXHXDb/R6cBCk+nBTo9kIJs2sOYY0yxUWdaZRSYqfV3hHYATrZx4idq5jb6szBIj/awJ1HST0mUh6clxR7LM6WY2VONnXvhOUH9T9AXQ2lTAzmrqrSlSKY8iIB7Tuuo1+235riRGXYg/NKg187IIufg93aeH7j6lMlaZ7WOZGMALt8lIkLbm46aJGvThr19lTofeWtzswJI6ga8DDV9K+YpY4r9DrIrh/Jof0dlfNHCRDSGpTyHtRTtGvXzco7UvPBa0iWM0mh7R5Uw2NqqBrHpLaKL+5UNpbbhqfZIPf/emVlfWPUXifMxpT1rIvdSazzXvWUJ8fYOM5rai7E4uA99jCmtXO6Jhz4sd5SHg2W7DpyIBUKCL7N6ny+xQ3Zcvpcp/53Aak96gX4liANiGSiUDjS70u5BVDMCrw3TjbWj9WE048yk0o5r+x5Pah/YLDAFXh4YGPL5Nip6x72491qOdNAhhgqWVOgZUNtZxVbqO0HPZlUgbLNMXUdfkjKjj4D1b144+Fx3W3xFbzlzHBpzGL8uiPjAbqw6zsdt/YJIfbRNmDMUAWmdyUWxity5AJJ6yJe2ICBQo/uGB+uf14A/7csRrDyD1OVOhD2KqLPjM/9pBEoMddDvMS5a1xfYy7Ebl+VkhvYfq6iXQK3ie6feLmN5qe+CugjC2XOZKdKRkbOnYiw8YgEKyMwawZpo92vRiNs6caCtYDanceXDxnfPDZdCHg17EVQnZ4G2eCf5JYVmm6ITY6EAlR4H5RKGZWEQi67KerGMTZ/YNOTjTU12oMY9g/a097swl8sDoeOUjNoqJAVUcj2T1nXCmK69OotLnhGkSIUt8QsHNm2dVbHQvOtXGFlLuunlUgc+MnpTYQ6BvwNc2biEt4Kp9uiyT+LvIW1VPRaE8YE/7sEfSKdrjFwYQDTlXX9/wvj97Ywo64//3V46uaG/MVWYkaupW9QtDTZUgHVsXLTH4dCsbqQE6SzrALZzAAOwY71sW157QFOXZXfOSmc7PZUB6dIoxgDrY5b9LJcBw16eCbBiAb9c/hRPjnBW73QVX2pZV6d6WRcylgcNguAemYNVdDMCiWCnkVJvuMwbQZbRhvUCYcHWBdxgA453cE/pDiQEEhF1sVh4QTWpgAP49XesK6NkZSicnfqg/hF6GFcRyQPdFVOSm67RGPA14exOBegJJ9LS1oS5ztLeXQQLJCMc8mRBLoRCoWvZ50VDgkFedgR7TagrwhhASqOVr+in61AA4DuEx1FZvejWOMuKdDI+GxUb3YgAVUsmft0U5lEj2ZcFzeZAlKXRq6cgmO5cQGVhhBAOoncsi/+Ga4YeNAVTJ0r3e8qyFtLLsz/sUufBH2SWH5JhADpP/1al8B3mu3+nTrA3p4pi4ZXcRB5UuykUjrAcu+wSknAdOJL9PZ9zvXKu2PTE1aaNnNmqoNXYe1Hw4COnNp2i7IgE1sU1N8aJYBLNGH10SD8eB4CSgYQxA3rrBaNMH0vUaIh6mZWwm6Ub/dygckeawCn7ZdDcKjqG16R80HUjCcjg1ySKu1oNbLlnq6pK25eYFRr3bilzmIRnDAPT21fZjMYC8YFFzu93zfYQ6xYdR88D30n6cYN2ZpgjmSJn3XB+NR/aSXTTBK/sKS8c8gfceYAIjiI2GSnksRaAETcW0cXpLVbL0964J4B9eGwMFWiyLUdBac2yJ/Qa2pGbHjulW7haIfFfpYn8fdJ1DoK/spUb7g/fHZHxsH2dGGu7n1zWu1vwGMnQeKmObekT6yLHd1cHNwhNm6WnNJqb6EDpvjY0lCtoDNkcJ5S0Yn9Ue9fGtKhO246AF1LSYLjuSk2ikfpdWady1suhXqw+/UHVnxyJ7hQHuqJhmYhSxDRMbW9DJ4JHP8/WCiTdJF+u41xmbzWMxmQneGECk6/iHtgJG2Y9mEVm7qw1v1jWd2qFeT2C777bZ6mrZEnUIHSyeELIsaSGbEx1jIuCMFrHbSy8l23RlHuZ7+0Ndx3J2K7SDP6ZBH0Blu1bjT/zw1w7WEr9O5mxVmguV4pBnrejZKj0VC5Ia29bYYd5lXkc5uugNyAeRLtpT3Ue8LO1oEHyw3EB+jOqicsuCVmRYADnGcFmZHKSqK0dZOiJqMgwX1ygwLCyD2IhQPCCcWaRcN6NlnRI6Efl+VSmUkEGbOkEQJr+34Qp62Fdmk+ye7NL4CntItl+kcUDtcLH94GBIj3Ch/EQ9OHKo64rvZAv4t8ATA/itwK5R0SBp1HGX6ggmAw/7qe9Nx/mUh01Phdu6jJnhKEKEsAb4jOe87jmTNh1bDc25+wdEmCzv3qk9AU9ts35p8d1aJFaN6vvRpphEqjdumwKjNjErg1mD+2kJxh8pzSgfwugGyEykoTNLzRxV7Gtwjh2SHdfRZQ0qcTdhmYfnVwWvLIxFv4wo4VsltZ7UMRyY9yca47d1sGXUsgCki2ZSApYismaqXBm9CnMtwiZpxX4/e+jEMR0ozCFMgjxk6nXnb3Sbm6CP0TP4+LRFUoD75Qk95DSXtW+wxdUMtSE9XPTZxO/0QaWw9owOoxcG0NuhLYKXCnXE59UE9bYRpsxQBT1ymQxL567yVfIsXuEniIuZJrcUjRP+WvZ0kdE0QC1gRMyfmvQJiyOLVc5DVqBNaMWmfSmrDfODiLQvwBkcDd9nK13+mn2kWFGtZM1oLLXKePu85zhWKu+1h+Nlmlx/vYcQ7MKMcJf0pZeU/TQW1XTEKXOA2e1K0O/PaqRA8BFPu5OM62RhgqLdMMSa3uRmS5NDcoZWwM2U5J1oL3e/WHPBZ5GzCCC6QwIZVsN6rP9VLNGg5bqU2FIBtP+MbuP1/o16XKV7tAb2VXH9FDruABL2DjRbXps5LO3S9GKah+kcJDOf8/GjK+1D2earWym9flyVfXVe7wDv/IUVSzGf+4WXFtY+4DAV9vuUi68tKVq9LtRRpLm9716E1o3tsabJsejjuxwJFCMV+2lVJ7+sm323hyxqgjdYmYv0dx0fuhg8nd/N2smnULUzt2B8smKVhbb1oJ3fYHZr9/fdjtjdxb7xHxBbOAwb5WfW1VBnZ7RLbgJ7SdKl7MeIq8XG92nqJWSip+yE8bbC7dfj1rzpmyB1l4/JTg/T2kI5dipGfzIUigzOV3KTfvf3pEF83j0vj1RcL2hYYFnOymsQNBT2mKSklwyVJufTx8EASE7VHSplFizZo9vUQ2yWnvs97rCutw13Z2xob7ecCECXIeaUnsfXV6mMwwY6HNG4y41pERnrWXxIPxNISuXQA0qCnayjvege5fqzylCL50dp5uXiKS2ocSZGRHaFJyjkS17jLEzYKgYPHtwTReG8FXCTBndk+y0iveoQ0qB1vFP6/RYS+Mmdu6pWgExQ6vBm/HZ/MfMw+pT/slCwz15+4akp95OZuoKxnfkfTDshRwydbDSo9Rt1x5WOzL/czsDHPLMF//MNnA+A+z1iWqJnVxk1U07EA+t5nMXm0gNP+zR7uWzAdlvumPp+HXAA/CnW0MbeH1JJZa/fmvkrJzAZ97BPdftgVGqEohQZpcvmHWIXh8+7oCkb1M/4zhksr0YIGUtHv4H0tN6KqNQTte7UZEtMQjQLq8LNwZfUM1oHu0ibyWDHeK3OruDbjOwELnS+L3+aEjtkN0qsVssYA8AX5kcOnHbRDiBUQcSPDquWTVf0MIDQ0u1oJ0PRbNilwFEuXTr4uHRaiv2jWekWfDXvltige/afmiejCYcR3aONWldjohIdE6T7nlY8L64XTsqOF3jJPuo2/GfPp89hR4EFD9C3YIEBOAFhZCsYwJdCyJbVvXKnwwA2vxJZ0Xefq+eJBQajp/KnhRNHVsDdUPRn6Tnp+ygEOucF1bteyNF1R+8bIGwvTMFnSZ9ajnS6blbA6Gf/KqfHtnSRg5H2hRMnFNGWN3QeIpezK13PID3J3LsoWZAmeN3w+/0UiU83hlGKkOtE5vOnGMDPn5DT+2h8zGob32yNrELcZvlQK91C8+Z2HM4KcItOTEFakLMqCTrGAeQIAQQKQpUmo58FDSAjGdAoDOC61G8XcnhCBE5G3I2JDP+AfsBFi1n/YhJlCIEs4RN5USAZj++lthZaEANYLIGssxpP9T32iyXBAOr34MIYgJFjPdro8FTkbqjtKBiNdf9Y1t8HXQr0QTEAt5FALxDyVRQu3esY1Mv7aQVstEQjh13QXCD0y+yWZTGjuVXPm4Z2wSEbmX17KaZ5+/SKrOLVOwA6cc/oLEFREbz+shnJAEYq8KCflUWuXdB1DRRHYwDlzO3Cgf9yTwuAjtrqphSn8eAYAEwtKN5DiVphbmMNlegeuZEarOCuDJbizT5LAJ/bIlKQzzGAsNyzU5Rvz1wusmt4PSjSe+6OZWym64419iv7xwjrF5BuCiRbAwbwI1vU50MZWvVfInJIj3xwVYir0ZARmiOZD3yAAWwJf2zaRlvStZLX9a+AHaYYbl/J/UvV1cGkp4XMB9+xu3adxfzuzX56AA5J/5ecEb3Q6PrlEF60RHLPGiWKRpQQXbeESQb34xeUOktq9iS3y7a6554ECR48Bl9Mhj5hAHP12ZsGwOuK+Lcj5WvR8CQHNEeGw9fj7AuamO9LZrfor7f7GIBceJIvWOmSEzcABjdOv/cO4Wt0hWqRf8Mk95dT8BkF6I7vi2+ZrAitzhiqNh7RwLc1waBw6lOZv7kdwoUMVy5SuI804AtCpVokeHiMDjCLtzN6BDJil7nkY0K+SIuJfmstRoFqvmfYYN3m1+OJPvOnFf1TE1ANsP+fAjvIx0hGojKWZ5ByFTp3SEefqqNJe1ISMswB6n1al4tKVIkdDmeMfsrkz9XmJnsN5x30YS/pFaIIIo+UXfabebblfrCmWwYOPXbWFDbiowjoSJTZwurTdCB9cZdEXnZihATko7Kd9eL3rA6oRVFtInNgy+U1YbvWyDGx7rTdwqGmYYKopWAyx5tGcbhxHeiMAQPoU+e+qT2R+lxhldey0AZKV294EqGZeM0KnjsvPmMhGk52bh+rt0cfBIJifkZaXNGmBKUpFdDbGDvofqhuKYxXsCTg9qArLFm2UZYQ+Hy8V8RLmjuPktjSW8oAZTaraF/vuUQV5iatnxSt0SOA8i22/psNvK4SIsXjag2+OO932aNmuARVLtW1cZ2uSlkefDWdyursRYbBxnCs/9que/vuERpYuD8W2jpHYBlK53E6rcgiD1e/3vzW1JyIMDZRBrPu/u54xhHWns5rAkDZLI5dWy3aO1HHOXJDgBD54mBSff03T8srJrS5kNyQAuc+g/yvnbsqubp92yNOLpedx1XZKkhw8OWIbtsM4CF9d6XNnBpLkWRAa+RvRPyf4lddy08UbcfnTDN1vFcUhMOvf/UGaDd5+UsJCDoo2zwPr66cyL0N9ENZKDlRpLi7Gr7LmsmXs9/S/R5enGpGNSKVu+oQZmvNtSshvraSXCTWXMzBEY+jFaHpl/1uxPP9l1B6x7XRRI0RWikKC9fBhVMdsTeNFIYUHaqCUs+iSzNmDj35ARBq+8ZuD29li/1rdwxg3HZEV47WAEiGLRzcaFMfHgq6LDP2/IU+FhdAwZEPtfI9z7zmf5xf5T8Z3NssrTa+HV+2TPNtt1if4VRUsrGI2K+f7WLn5WoPi6eP7EbT6y5q/chvZmAxAAW2C02S+eZ77XZ4NcbniDtQb/Dh7ktmDkYQ7+pCAj5pBhNHDrtT14EColMI39JtdJi/iZVZIT2tLYJLsaU5Z8wG5gxYUWxhk2pp0IjjkFYKP5vSpnFSzI0ZTKx29Cix+q/1U/4ZQyr2T7KtbOKvsKdtGx0eV5XADZzQdIWYKIEcYKoDhdmJKNCr2JMsr5RF75YC99RPI0uaMswqdrbW0z1W8C4HihbRzI+FlhxGJ8y+44nVcwIvmmjR2AOgbsZyqUrS3hS9keIOPmxEbU/N6kxJgPalEAaElv4mw2K72i+h0+tH9VUsL0c3iZXQA3C9M3Ch7ZKHOaVwcg3tIT4bbcLuCOkw6KkOxGr/Uzi69RF33+nAcFe0UTHZwIJRcIQlTjBT2hXLTMIJDfEg39AhHd3HIp79HgGO1npAoI6oG0JDLbPeJONtKbPIPkMez0n3UjWoXWi94/0BbtWmKl//9d/qQdoWcOZnBSe++sLFE/yXMa4SReBELthDQ3x737Lcvb9q9rYVeQ9jcFcoyxXkr0ZxOo/eajFUl0ZDRP+GfJaxpkSWkriAcqNs88frgdWtBmvrlVq7Ucs+S8/rwM1HHW3TQ9ZPuJwtrkPv90Oig92LJSc2z0sW9DMvFgQHzlfNv5EN6bYkdfZf4jOyYDWPzX27Ml1Wd6XKy9mX961NeU8ci3/stFOfuHIZrAosMyammG2KKsHI9sFPXcdeznxNkbvceZ4N6knc1r30JJ9Y+HmbgrM5VVL2TZBt6EKOBvHtpT6MgY+0g/X3t9Jh6RNhzTwGqlVW5vXLSjGzNzzjGiFBO3wLHkq90miz12I874crGHqbnDtvHsaeoPcrO+d+LcZz+PwBznbY9qKfBq2SDZu0DtZ7MOh/If02eLsI7/HKl5d1A58Ro8mG1/a9yhlvxSygjuIglA2i1Zd8VeOXuP5oCbT59ZvBdL1p1eoWLdOdG7sGikHrfB0nuMjPCIRmQWVguQLyQzbCgm2BvR3nmaJBPGOWXGXpQM/seDFqHllc7SxTA425kdH2UwSfrugr4R6kbLHcMxGt8dDcpX9fp1hVCvSioaBEzq1o091f0BW5YNYueJ+syPMSiCvkNAyBfccNPCEwOpoHNzNXtzDM397c8KgMLBvdbZT9gaIUvF5C1siu5KY+o6HFo/FYB9/8//VDfpZUgZrGADpZDqHHOm1vUedGkhiAqR5kjOtWbU6uCdTN/ET2WsxNjHDGC3l/O3Gmb7CsPsjpfFU+BlDHjgHspiBLwP/7RNsn9shnUoS24kk+ZK1Gjek7n8XhPQv60ucLQsXbYgAiA9sy1xr3uuaT4P34tkWIS7PaIKcBahhAD1kJ1h8Q/Ehr/IOCPwSQs18NgpJq/2vVs9sjlGHjyPOvGxMDD2/diJiW+/Hi+H5alGpzFdcwOzvOzzQxGgrHZfQGsbyLrGIB80DWHhQF9yKOysZSMQAfAsQPD80BQc6qbbWB9SXGfQK0Ou4bb9DbaPzDAg9P3HECil+rL0zRtQ5DnYXUr9IwgL+vkCWbsg2giz8QVuxENzHrhjPyqhfPt9L5IGiy1Vyt1zpdp3lGUpWZ9h0MpBhA9S/UL/lfQ9GpFjfexSd3l5sLkTIUvRXiKRH6qI9pCJc7seX7PvmQJX9NH1xFQljfCIPeFfUci8fvcINuiEv514j4KNUTnkBIjFRQaW98f6l0/Hj2mLJPGCc6ysGHpUQnvvXRy1KpQnzSguFsS1aXNuvdpQAjQyMPw6FjWc4qsZkBGwjRsZnJRD+YlXIszaIudbm06mQAcLw1PW5FohDxmm0F2FsvgwFoxV5V+IK7Ywrxo69+4p2FQwhXXe9Z5se0JlSk7xPZKJF/OdgQrCBcPVYMoAyUKIsGNhqji/3Uy8nFrNKW1KIF7pdGJ5uQDp/kqET0DY4vmzvUipK2Jnqo5a4r+DzOCbQvFfiHbiDgNi0dQi4WxvwO8SP88iPTep+3441fzn2fKBa97rAydNVVjqAKdEpbUdBu4MAmvX/Pk7LKYVqErEGR5KqSQvdsaelEGK8Ph0bdFP6tgd2jVE2voR1K3G+z3WzQKyrFRR6lyCr2A14CFJ+6LA69LY0JNQH8xto8wQCE4OkM6bJKdw/aqYk7uTMH2Qz/rgufF1uRX9jfzkhUI5z050P2UtVB7SPH82QyWiZfU8MutLIvb2caBXTL6LU0w5RgzkQV+qEX9aONlcrV0+1/BdD2TqpyXt2Vy+RjEk5p28iFr+H7b3Y2s2PbOGFlFrvDezP7RV/TBGmn6vjobuw+8ydZ4u5+gT5ZQEywL7TGKb2QZDAYNRVW2bZfMFKEyA/aJqpMFXVYjnngizymg1nFuTffytJ43U19Db7kk7MY+0sqJQ63ByfZCnl/h5O8Sg9UmZ5dTbTekmQ42DpJuJvVKLKad4pcmFjYqlA/dx1b8GH/Cg5TfqkCO9Qljz02lOlwWnvKh8U+Te1ME+LnyYXanLoacZLgj5ORLPhLPsr4pEu+ygkDAD0RMn5fFvLdcUyp3S9RfHTHXeREsEp6AEdUB3sTV7ACAyBaxK9cpzzoJfsmM2KwFnD8sGniWQvhCIPakghb0Y8A/Icgr2OTCNaw/vF19cZPj5308gpeq5KHMedzCU98/M+VWMmCN4SN6vcvOHj67NUpVPCNzcUSsC6UIt7QjanHfyNtkt99/tBLq8FH4mwidjuVpMhHK2J56c/DAlCxwAh+aCxWWos5fzK99BcGOHofVmrjrX7A/5m6TD+ULc+RWS1OAOwD0b3KfnhTNhTGzqCaYAdgr/hLh3cU4e1NYqhn7NodZPFcCe/312u+Gsp3I41mr18f9juCi++hSV3gkpggKn0abhEtHHxOol7UQIQ817f/vtHWhpcXtumL8qfU/NCqPdAE978Cc8IrV3vVqmc21kxdaHpbS26TDzpsqaSXMsfTkmq4OSpElt/8Id3LWbd4D/VzTXz9vShp7FoqC7L8QsviDLsfTBB+lPfdn/XL0FTJqN68JyDcw6RRk+aW+MfYti759XO3Mw9YhUajsq+CrCaz2nC8DWtEHQ8AkPvL77fy0g8aDXaIYeP4l6aWZ/qdmszqFyMowIlNIAYQrnzaOGGq9zfw7pIkhAHOjjQ6qXDSmvjj6nOpr2hfiYfaGhl/0tGsAVoBRapKa7A6V/DzFCZ9TA+FscFXj5bmr8V6x70INk/siY63mhSdi7blp2cbGHzfzh8rIYRAq4PgEAwge6jWsgdAgeXUTVv2NUr79cqCpubhsbp+RrZXmvuf7uLN6JEY5v3V1J/uH5t4ll+aCkf6EkFpcUyaZFgMpaAdtJUwUrsMi86kM1RIQ514hJOsRTvXGysAGTupMmdh7QOWaeWHEq9wC2RJCXT/zySo/33LZwWqpOkyP2BwID74liBOfaWvnqCM7RawmGx1VZDrT2mK2yB5PbhS2keKJbnABJfiKn8a3aZLmUeKNWa4r1KbndQMJLGSNY55SMl3GJdjXmmqW/usZ5MU6wIecrX2UrNn81H1OpPAw4i5Eo8BKZPRbov2oY/W7NufxW+9nGQl12s7POGFWaLohPm/NI8Eip4kykrGZMg6rcXCKrt+tc5dWxSzF35mt3/C7cXgNUeZH4zbvKX5w0yOEjvPdzgrcl9eZUeB+/l2XJzoODRgmbpECDtj7u36W3J8Fd4RuXNWZI38ssM1+BgidGT2XkvUdjSD5qvl19f5lVEQ1aag67XBVtzte5xnpmKG9LR4h3ujeGPrxoLrYzPCTiwbx2xG4voC3hQkICqEXM2JnsoTx/aJ5VGCOuRwZ2oUjBr0M3ptTBXvUZQZFOkabcx2YRA9m02eMHyXsd0hN+IAS54fW2AAKU61N65lc5sIxkTh3nVtGvBFZo0LT1/PYnENgOTTri/mZJueLfMPr7FKZrRH7uGYLMVP18fNvz1Vk6/lhvKOXPRRHozsG2q57qwayonEeQZJvzGD0S7t7+sJVRaJ5QkrcI2exjBaBoKWjVyQCjcaTFJLrPK/NBzt82lwDCfewiqHeDPIFv7olma3RngHL9j/drz0KRalmK3TPx+Qr3N3tmfydAvE3ZYC9TTIS280vmYd1A5O5WCbFQMtXMVEFT1or1KSgLPmJb3uGPhFbqgrdXFFSurVn1Za/RqLxiVtkkyiz62f7f3XYhYcUpX3PWHMOQ/+k8VEhOkyYwN1J0y6msxZ8fnWs/jOTJdSGSUFDvt8aaS9ZnFDvlqdli/b7d4voIfnvNy1xN/qZV7L8M3dzPUeFxnyAA09KnlOLlhCxpVSXL4JzzZEFV9P3FLITulBNs/nwKTzp1rG2bGjMhelkvIEMgZforfDKzh2vegUp2LAq7rjBvKjnu2HdxRRUAD5wUQYp1gzBgCbI6Pikq9dGp74JAikWpS5mU2znQvvm2nomLPDAA6yL/fVmIta6Vk+WLi5oV92NZmw8w3EcbrUXrxyiZ4oRXjU6c4/P6YW3Lz5o5ZdeAANajCd1Pt4D5ArWN0lyVoT6ti7iqKdQ9YCH3JmbEIPIb0w4dfnYm3cfpcqU8d1sXfFTdn2+bMKM0uGrw//tpXBocep59QIZF7Yb6HRTMrfmsmXjfw4T3+AMiURqzm7KOrF1UGIb3T6C4QbKfOr8Veq+VHfDi6HGoGevG7vjB0fccXu4UJ6w3b42A1gzJ1j5iSL2nTuTYiFkNMjsLi6Od6lJ5xHzlUQLTgKodewt/81Nuzo65VdwU/cL9rnFvUKnxr6VlwnmcR196wgbRMZlr/r4pUtT/g0c2C18avBO70/k7wgLjBXKbmmEm9pjvlSg7dRLwaA9wX/TeiYftoHIRC2h7KudJyQi+HPxyYCPQHKOrqv6unVTSqVOf9fwOk/AtcoizXeCIBrjEziAMilROYZ8ChmIPY9nWfVHptjuZtFe/JvMWor2oxXvvSuFoxqfU5iL8dntbMJZYHp9naLuP1C7sWXsbEjrmKvJrNmLYQdcZyNo65pi5vLwTTfWLW35rVhmne9iGnGc3mgGMwqla2M2uYva+U1FdhNcQRWmS57HoiOe7Z6Tr2DA33kkClTg37b3zy/fYHCE1W+AivJt5G2dUreBiMv4k+B+5I/qU7MMvY7gNo159KhJeuqxyYJ/xJmdX5A+yUWbOV/Zx76e1DEt/le4oh4IPkIBTZkHeZq175Yj8e9qVjputasdP+B1rSvsT1mmBMbBPzpBslXuBZbezmftHV8A5lsMp0d2A5nKL1cnzwOATshN2NvOlkYZBpMhrPNcW+qa0huYD8/r2kCqZ6EHDsg9Rpwr33r+p8HZm3L76Km70YQWux8I30jf4Xb6xQPPjzrdTJSutaa9+N7rCZ9yxmcmh50J4Q6hefbfNvYwQsIc3sM3p1d+wk+bjr3S5xQTHhhqlp+8OVTkXCquUq9nW2ET8290AGVwI+14fAeV21jg6QSuNbdQItYfbK788pTxu5ID+343Bl8UKWS6MESnsRSpPvWjDM/v7wLlz2Og4dD74WNe0iB4jJCvdHG6gbc67y2nB9R4e/R54u93kF4FPNafFR4BozvocpG+TTh14O24lztaQCrPe+PMNEwVhvm/P/2QitsDVYlEgoDXCrRecjcya+sMjeBq6vwpttfFc8P3a33VH3Ksj3cN9ZRLwNIubQWBbI7aHRK/bnOAca+aop7RJ9Qkq8jS4WyXfaROtt+tCPbDFMZ8VSsWy+reKd1S8lkGsbBICRcKSC4UTHgwTUX4V7uJhHlnE9NroX7Pc0d25eDYhv6wHuXFNbazxUbi9rUltj45LuMJu2ygZxouBAmPrc4nX9iw+JA8dAMhWOaHioKKI4oH0hi2v+Y8iZ8cjXCqU/dczgVbTalSWUGfklyqlXx9WP4NyxVFySrIN8LS3+daixTWJlmEo/8HbE7uFJIyzT/5tnBVkSPhlIT394iRe9vf3qPge33o1q//IjcY1/F4jOV8J0scqQkaR78dApQsRZi1FQpxsOxzz2mzDEJuMft/wzt/4+GTZpyzzKo/8bq6AbmJL3baIiUemlPirWB5hzHLotp2EAUxC/qc/aL88Hs6/Irhr+8m0v0CP7lHd5aBJZ/77H4ToY3Z6MBBgYu6wz3ydD90BTU+hAMvZtqLpetuFWr6xcwnqebwTOen+h6aFHCpd2anEy8+TeZ4a6W41yVcIeDcmEpTmDoRH8GyL+WpvJCFKHW8oQlDWz/yuXaKHlq9AtkTz3oCLXV2BCBSFyG6OYydt+tZdKnOLYc7iulGI5Q5Hc0O0omP1GH4bmFBRQCjN+D5PMnzd+dmMKK8lVrAzWQ1u90Ned94j5TV/ILQmFlbEWKuyfxafsiouvC6X8D16iW5Dfpz+BBFtOFn36yZcvDs/E8xJ5TxqbRZzupeij1hJoTkH9yMjjiLJcHkFZyBpGFApRxPkqRBv0nwfB/sw98rfL53FG2Eef8QXb2Py3oxREqUrwMQ3zAB3oiv0ukdosZqc2Lej0KjEPHLadJpEi5yC1uzO2JU+0pGGZsCQ7X97HCVl4MKBaGMZvyRAfQGu20RsD3bNDZ0AJ3ws6XvopWuTEMNVNioMVb8Z0E4qwQLoPGeGjkO1IcZTOve1dbatjmLen5k+Fu68rZh44TMOfgO+Kwk/6v+s3/n0z2/vBQVbIiRsrSwLp6OJ/snqbQFNatf5SLDSW81Uq4Sf41e35itaAebcOcA+RrbohbXM9dLc9Li1RvFhDIDXsvy/5HJPZG/a+Vi383thTp+GNbVc83rPRY7gR6BaRq2Ia98nIhj2XIFq3QFN/s8hM3sxJUZGWPrtZwdOKoGjO8tVzybmwm5x9p6KOYcwMyJe89+SBAdeK/egeCWfgfUEsHCOyh7g5TrAAAxbEAAFBLAwQUAAgACAAKvFVDAAAAAAAAAAAAAAAAFgAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNLK81LLsnMz1NIT0/yz/PMyyzR0FSoruUCAFBLBwhFzN5dGgAAABgAAABQSwMEFAAIAAgACrxVQwAAAAAAAAAAAAAAAAwAAABnZW9nZWJyYS54bWzlXNty2zYavm6fAqOLjtO1ZYAgSKq123HSaeudpPXE2aSzTTcDkZDEiiJZkrLlbPduH2Xv9wV61zfZJ9kfAElRpCyJOjjebhsbPOD0f/8ZBHz25WwSoBuRpH4UnndIF3eQCN3I88PheWeaDU6czpdffHw2FNFQ9BOOBlEy4dl5x+wanXk7uOtaWDb2vfPOYDDAYoD7J2Lg9U7M/sA64YZjnNjMpQNnwE1MoSaapf5nYfQdn4g05q64dkdiwp9HLs9Un6Msiz87Pb29ve0Wo3ejZHg6HPa7s9TrIJh5mJ538ovPoLuFRrdUVTcwJqc/vHiuuz/xwzTjoSs6SFI19b/4+KOzWz/0olt063vZCDCg1OmgkfCHI6DToVYHncpaMRAbCzfzb0QKbSu3iuhsEndUNR7K9x/pKxSU9HSQ59/4nkjOO7hrmDZ1TMKYyVgPm9TsoCjxRZjllUk+6GnR3dmNL251v/JKDQmNsigK+lx2iX79FRnYwOhYFkQXBhSWpV9h/QxTXRi6MHXBdB1TNzd1VVPXMXUdkwLD/dTvBwJYzIMUMPTDQQL8K+/T7C4Qaj75gzn55BhoSv33UJliYL8GHZ5jfCx/LPgx5YvTRSJJZdQsma4cVL+vjFmMCDxtMaSxE6G0JJOS5pgGWz6mU+Elkbz6FRHJJFVQJNlDFJtkYea3lr61VUGwLkj+0pG/evLG2o1xJYisgiGQof6pnybTVg2pubTnEekqptVHvF9OqgOe9I5p75hYxDkmxG4OaZkPTaSJe/beyTQoPu6Zx8Qg5nGP0MagkvIlZkaXJC/3j/4SJM5OCyN4lk8IpSNZN7cLmZikcoq0h5gSfIIYaJJlg/1iiPSgsKVGGYgwZDK4JQ6yZGkjKpXIRBQ5SNYjFCmzxxz4ZdqqMwsx6Ew+tbWqIWoiRhFR1tJEgANSFhdQMSjUYAwxaCSHJ4bsglrItOCOOsiEOUpja0tNp9AQ7mF4A1GCqGxMbGRYyJL9EVMaccuRU4cuDWRhZCnkwV6DrdZ2Guo7iEpqQPniKPVLdEciiAuQFI5+GE+zBezciVdcZlFc8lDV9iJ3/LTEOn8jeJpVq4GnmjtE7bkW/OVHZwHviwDCimspCAjd8EDaSjXCIAozVAiBo58NEx6PfDe9FlkGrVL0M7/hz3kmZl9D7bQYWw2t/PiZmLqB7/k8fA1SIruQHaKKW8dzt26xfBg3ihLv+i4F2UGzv4okOu/0WJeZpmGZINYWtgHNO/2CEqtrEGwz+OWYFMOb1OVS5BnrYkJNBwIbBu+kOtwtf0UNUw8sbkrK+EyU9KBh4peskNeX6dMo8MrXceSH2TMeZ9NEhWhAUyJJugiHgVDQKv8FwY477kez69z96b5e3cVCNlET6A+fRUGUINBIgzGokJd9Xao6cmZlLazqYFUDF0zyvfI96Rmqhir7ulS1gOt6ajmlpKCS4GIYP1W2BjpfkDIlMzJ0moZ+9ry4yXx3nJNKdIPvppM+iFuO22KfZF99np3WJOxsLJJQBFqMQuDlNJqmWrBL4fzobJqKK56NLkLvpRiCSl5xaRYz6FpXnU/ZE64/gYb6eQ4el4z9C0xVP/XEMBEFiYGKijW06i2uCnXjserq6ySaXIY3r0BqGlOF0DgBSYJJSNuxOL2z04Las9RN/FiKLuqDFR+LuXR6fsrBB3hV7QRoUujEVV1mfiYh/oqn6A1PU5H0xej3fwWAxiTyRBCgwe+/JcgTIbqcxNMg7SA+zUYRSBdgmACP0HdA2oSHITpK3dE0iEd3qT++9cd+1xNPYAZgIaTooWsRg04DB8Esg/xL+xCICUTYKFNaoBSplIZnKnaXbEdR/2ewWnVxmXMJ3i9VCaU8HCbEZYCfQx7wO5hBlZ+qvxdAbI01BehgiWItg7EQWnz1hOEihu6U1ld4pnidohnEK7jbY4xAwMJ61MaQcYHa38Fzs4spYSa1LMN2sOWA3Xqvcz2d2EgkpKFYsMn6aU2GQAU0iA04w+lEAH9KvF5I7ipQofU078MohlwAOo8HNsUZV1AmDZRxBeXvB4NUZAoaQyPhLOVB3ksayOwMTXztNSd8plIs3k+jYJpBfgqKF87zUz3t3LtACiWz35nyHlgNZpmWvBr4M1EadJBk/z2YikW9n9vHDDzeGBK+VCd3ublWF9/6HqhFOdkNBAYvE5gFDs7iBMaSneTo9xMBUdS7APz7DDql6FOU/pJkR4qbT7SjX833soca601IeaVLtRybgGMAGWzH5NXzfvYin/Ez9Cd0hLsMJl7M5BhBul198KSzaAKaRNVsw4vtjIPlKIJk0dfFttZhruOkS0CLIUF34F+PQniiBdvo9mzsONTsQdKHHYvtR8WXAH1VIP1CQX2MwOyQ9pBePQCmdDdMaRcfAtOV6vONAK8mUyB/OAZprWsR/dAGlG1qQHFuQFl7A2rlBhS82AMaUDAaezGhcWk9a7wEC6Sd4gZWNG4aUKtg/XYmc+VwXn0wvFTO2kZEeKV24k1FCYSunSyRUpZMUnpjVvXGOSUtpMl4AHe8kkcNW7B/Hq02Bhupu4U35JFT8og5hb4zYycWtVZ4POcSXhZlVxK/DZn0ss4k9piYtIMiUZwzyWD4f1uPalb53d9fCneUpf9oBqwPy7mKr5Vfg1plK9s7W4sW3tai5sNq31budn3OeS9DlyefD8JQoiE+sQ+ffs4ZahP7IRm6qaZC5M3j+fLSq4QH8P/6uGqcR1UEnaKXEEvpnBRykEWuP4HX+atP6682ibzGTTdrNCUCsgUlE4wsD3RWk/IaGAovV4eJQNl9pqpB2SaEFYPWyCPmbnFlg7hrd5TwcCxy6vJh51xpMGyTyZedNvIhttfJu/msi/HQSZ0Jm8zWbcpQi2luIECjfJqjo+wJOkeV2bogG/Dq6GQMF9lSbAfTUK3Fdua9rbGKFd3dZ6iPtzU+q8G5zcG51eCA8QUoFFIrErAGKLcHB2Xlik/72KkKihtNJjz0UKi+v16ppZf5dz+Ozzuzi5mf5rOfZsXTC91R3nzNGs7Fdis4xNDfmlS5wbL5StnZx7J5Edmq8iCLZhckF8mj2dHFk2N0B7/BDrK2q2bQz3aLZtpZyaKvi23xbqLGDoeaUUWt8BsavdbIGY8HOePw8kbvRw7uvNbo0f8r9MyV6LXXWvPxoXc4rR0VWjsytP89KiLAkwUnLOP09UFsM1ZZq8gfIFjZ0i9fDjrQd1Is7c2ds8Lpk2H2OVIgwmxJ8UEVcaOR59a9eD/h03S1J2/gqtvsF9pNV6oOAO21GMrnNVylH5ZQXjQg46vhSvPuCiB4E6mFbzAHksFcK1OYnOLeRRBEt8JrbOOY6zurWcv5WFtk/OKXUDdJ9T4ZfxIHvgspUYFmIKOsy1BubdETbG6GGQsRy11I34eQ+Iep3E1e3wWzsDxwsxWfzZzPtKkb7Rjd/zCMxjszGrKeR8/qzRf2nhabhC7C93zU+DS2ycregWzXQXdjvLkncZD+oW0U8uYxJg/0YGHIm4XswdDYGduD9wjzh32BV18sCO6GUVi3qLlBNXQAotDlVEtV3cS+9qXZGue+lr8jug3Pm9yqC1NekHXLDXoq5Qpm0fF20cKOdnxxncJg7di3xpTfbwoboce7tXrcmpjDuaXyq+FG8cca9n1gp9TgxD5SkYdixAmtBQjWH4gTt8tYsZt+H14lTow/JCeWWKcNtqcVBxDahszzb6wFqHtKnOrqstpwsUfApHWJUzNGuswjpEu9UPMVhNw3XB7X+XH0U6tvJZe7b55/JEsy9+STZfRTj3Um7dLJyVbKoXEieOePSgdz3Gvk/wBmaJFtX5cSuXQ9rfZ99D///Pff8g+k8GPl62tYh6nFkaQKk0c8fN9yOU012dgluVHo+Tp7hOrf57WjpiTI7QbzXQc7HThZyke74KPRTm3W4L+4BKwwX7UMvIYbxhbsMP7o/FgEoB9FgeBz+qP6ikn1zNfhzHaV4LmnNgnT3yCc1Wce8hOMC/u/m37utUgCPh0gYLDwhyJc7/bid8nynTe77a+R3dZQdva8teaVmGXFitAnv0yj7PO3YCP1QTn0FsXgxPVjeTLjOX8lfvgxfhf8JFc98udvj9G3d/nNMqIyGKGzONzBA+vdXJafKkLrsZA6UZwCgwbl+XP/vXiR/4UTfdIYd4qArFgfkMcf1W4JlPtA07So42DToNhmPcPRQSbuUof2mOEYzHFM27YWDtStkz6yj+MBZM/HA5bM09jHPI1DHmPwJ3w4F8WnfuDp4QY+mFHtmWw+YIQRp0do37McYnsmtShzTOx4Hu6ztxfTLHrXBxPS/Tke5iIVPuXueJhE07ApbxUZCdUBYTVjfSLq3hqVZdxnUhvnR9Pu4MGT/S5ek7Y6tv1OzjarWs1dkAsHyWpSdoxw20Xa14/nlJ5ZO1FGDnlIbzEUew2ER0ktAJPHI2VU9boRTd2sjqRudG8FgjcHT+6rR/bmIYO9Krlvn9xAcr/4n7m/XL9y9D53Li6YA5H6PGyYh1z816vKVakqV1JXYnWota1+PMSJyw31w16uH4c5cLmRflxpBblqKEjcSkHiHRL89tFSffXL2JeCWPtc/dpCI67a+n1a9/t91uv3qUcExz3Dcj3DHFiEmsz1bGYPerb2+8Pk99/C7p+vvnk8jn/77QXL/P6um2d39/un1T//Ie+Lv+X3xX8BUEsHCKp6V9TDDQAAe1AAAFBLAQIUABQACAAIAAq8VUM+dkvjRJ8AAEqpAAAuAAAAAAAAAAAAAAAAAAAAAAA3YWY1MTUxODkxM2JkNjgxN2Q0MzYzNTg0MDhkZDBiNVxBdXRvX2JsYXUuanBnUEsBAhQAFAAIAAgACrxVQ+yh7g5TrAAAxbEAAC8AAAAAAAAAAAAAAAAAoJ8AAGI1OWJiM2QxZWEwOTI2Y2QyNGY2MTM0NWNkNzU3Zjk3XEF1dG9fZ3LDvG4uSlBHUEsBAhQAFAAIAAgACrxVQ0XM3l0aAAAAGAAAABYAAAAAAAAAAAAAAAAAUEwBAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgACAAKvFVDqnpX1MMNAAB7UAAADAAAAAAAAAAAAAAAAACuTAEAZ2VvZ2VicmEueG1sUEsFBgAAAAAEAAQANwEAAKtaAQAAAA==" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "false" />
| + | |
| | | | |
| | ==Links== | | ==Links== |
| − | *[http://www.youtube.com/user/SMUPhysics#p/u/34/RaXMgBm1fh8 Video eines hängenden Fahrradrades)] (Bicycle Wheel Gyroscope) von Saint Mary's University Physics & Astronomy | + | *[https://www.univie.ac.at/physikwiki/index.php/LV001:LV-Uebersicht/Videos/Rollende_Zylinder Video] von herabrollender Dose und Zylinder. (Fakultät für Physik Uni Wien; eLearning) Probleme mit Flash-Player |
| | + | *[https://www.youtube.com/watch?v=hebr1xH-Wsw Video] von herabrollenden Zylindern mit unterschiedlicher Messeverteilung. (youtube: "Versuch auf schiefer Ebene - Versuch" von "Noob Physik") |
| | + | *[http://www.youtube.com/watch?v=4OD4aDlAiZI Video] der Drehschwingung eines Menschen auf einem Drehstuhl. (youtube: "Trägheitsmomente" von "Wissenschaftskanal1") |
| | + | |
| | + | ==Fußnoten== |
| | + | <references /> |
Weitere Beispiele sind der Luftkissenpuck (Fußball), ein Mensch auf einem Bürodrehstuhl oder Experimente am Luftkissentisch oder -bahn.
Mit Hilfe der Regler kann man die Masse und die Geschwindigkeit des Autos verändern. (Die Massen- und Geschwindigkeitsangaben sind in kg und in m/s und deshalb etwas ;) unrealistisch.)