Kraft verändert den Impuls; vektoriell (Überlagerung und Zerlegung von Bewegungen): Unterschied zwischen den Versionen
Aus Schulphysikwiki
(→Versuch: Auto und Kiste) |
(→Animation Schräger Wurf) |
||
| (11 dazwischenliegende Versionen des gleichen Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | ==Beispiele== | + | ([[Inhalt_Klasse_10|'''Klassische Mechanik''']] > [[Inhalt_Klasse_10#Bewegungen im Raum (Unabhängigkeitsprinzip / Superpositionsprinzip)|'''Bewegungen im Raum''']]) |
| + | |||
| + | ==Beispiele und Versuche== | ||
<gallery widths=150px heights=130px perrow=4 > | <gallery widths=150px heights=130px perrow=4 > | ||
Bild:Springbrunnen_Europapark.jpg | Bild:Springbrunnen_Europapark.jpg | ||
| Zeile 5: | Zeile 7: | ||
Bild:Springbrunnen_waagrecht_seite.jpg | Bild:Springbrunnen_waagrecht_seite.jpg | ||
Bild:Auto_mit_Dreckspritzern.jpg|Ein Auto mit Dreckspritzern | Bild:Auto_mit_Dreckspritzern.jpg|Ein Auto mit Dreckspritzern | ||
| − | |||
| − | |||
| − | |||
</gallery> | </gallery> | ||
| Zeile 13: | Zeile 12: | ||
:Bei den Sprüngen ist sehr gut die Überlagerung von Rotation und Translation zu erkennen. Die Translation wiederum kann man in eine waagrechte Bewegung mit konstantem Impuls und eine senkrechte mit konstanter Impulszunahme zerlegen. | :Bei den Sprüngen ist sehr gut die Überlagerung von Rotation und Translation zu erkennen. Die Translation wiederum kann man in eine waagrechte Bewegung mit konstantem Impuls und eine senkrechte mit konstanter Impulszunahme zerlegen. | ||
:Zieht der Springer während der Drehung zusammen, so verkleinert er sein Trägheitsmoment. Weil sein Drehimpuls aber unverändert ist, vergrößert sich seine Drehgeschwindigkeit. Beim Öffnen geschieht der umgekehrte Vorgang. | :Zieht der Springer während der Drehung zusammen, so verkleinert er sein Trägheitsmoment. Weil sein Drehimpuls aber unverändert ist, vergrößert sich seine Drehgeschwindigkeit. Beim Öffnen geschieht der umgekehrte Vorgang. | ||
| − | |||
| − | |||
| − | + | ===Versuch: Auto und Kiste=== | |
| − | = | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | ==Versuch: Auto und Kiste== | + | |
;Aufbau | ;Aufbau | ||
<gallery widths=150px heights=130px perrow=4 > | <gallery widths=150px heights=130px perrow=4 > | ||
| Zeile 38: | Zeile 29: | ||
;Interpretation | ;Interpretation | ||
[[Image:Freier_Fall_waagrecht.jpg|thumb|250px|Impulsveränderung beim waagrechter Wurf]] | [[Image:Freier_Fall_waagrecht.jpg|thumb|250px|Impulsveränderung beim waagrechter Wurf]] | ||
| + | <br style="clear: both" /> | ||
| + | ===Versuch: Die fallende Zielscheibe=== | ||
| + | ;Aufbau | ||
| + | <gallery widths=150px heights=130px perrow=4 > | ||
| + | Bild:Geschwindigkeit Überlagerung Vektor Dart-Pfeil Versuchsaufbau gesamt.jpg | ||
| + | Bild:Geschwindigkeit Überlagerung Vektor Dart-Pfeil Versuchsaufbau Befestigung.jpg | ||
| + | </gallery> | ||
| − | ==Animation | + | ==Animation Schiefer Wurf== |
| − | + | ||
| + | {{#widget:Iframe | ||
| + | |url=https://tube.geogebra.org/material/iframe/id/322009/width/916/height/1198/border/888888/rc/false/ai/false/sdz/false/smb/false/stb/false/stbh/true/ld/false/sri/true/at/preferhtml5 | ||
| + | |width=1198 | ||
| + | |height=916 | ||
| + | |border=0 | ||
| + | }} | ||
| + | |||
| + | ==Zweites Newtonsches Gesetz (vektorielle Form)== | ||
| + | Bisher wurde die Änderung des Impulses nur längs einer Richtung betrachtet. Dabei wirkt die Kraft parallel oder antiparallel zum Impulsvektor. Die Kraft gibt die zeitliche Änderung des Impulses an. | ||
| + | |||
| + | Auch wenn die Kraft nicht (anti)parallel zum Impuls wirkt, gibt sie die zeitliche Änderung des Impulses an. Dabei ändert sich nicht nur der Betrag, sondern auch die Richtung des Impulses! | ||
| + | |||
| + | |||
| + | {|class="wikitable" style="border-style: solid; border-width: 4px " | ||
| + | | | ||
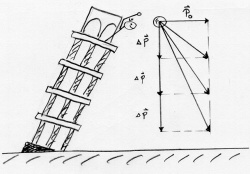
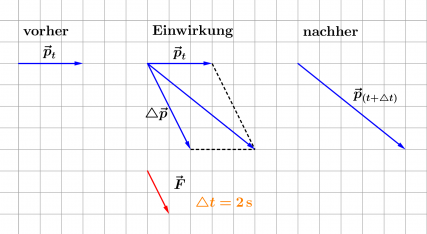
| + | :[[Datei:Zweites_Newtonsches_Gesetz_veranschaulicht.png|427px]] | ||
| + | :<math>\triangle \vec p = \vec F \, \triangle t</math> Die vektorielle Impulsänderung ist das Produkt von Kraftvektor und Zeitdauer. | ||
| + | |||
| + | :<math>\vec F = \frac{\triangle \vec p}{ \triangle t} </math> Der Kraftvektor ist die zeitliche Änderungsrate des Impulsvektors. | ||
| + | |} | ||
==Links== | ==Links== | ||
*[http://www.youtube.com/watch?v=cu6eKikHchM Video] von sytemphysik einer genaueren mathematischen Untersuchung der Peltonturbine. | *[http://www.youtube.com/watch?v=cu6eKikHchM Video] von sytemphysik einer genaueren mathematischen Untersuchung der Peltonturbine. | ||
**[http://www.systemdesign.ch/index.php?title=Peltonturbine System Physik: Peltonturbine] | **[http://www.systemdesign.ch/index.php?title=Peltonturbine System Physik: Peltonturbine] | ||
| + | *[http://www.youtube.com/watch?v=rf9meqw2SQA Pelton Turbine/Wheel Working & Design] | ||
| + | *[http://www.youtube.com/watch?v=IoJn9WQq_hQ WATER TURBINE PELTON COSTA RICA] | ||
| + | *[http://www.youtube.com/watch?v=YjZmWXbIncQ Pelton-Turbine (Aufbau und Funktionsweise) 3D-Animation] | ||
Aktuelle Version vom 20. April 2018, 04:45 Uhr
(Klassische Mechanik > Bewegungen im Raum)
Inhaltsverzeichnis
Beispiele und Versuche
- Turmspringen (Ausschnitt eines Films von Leni Riefenstahl; youtube: "Diving in 1936 Olympics" von "boxerphotos")
- Bei den Sprüngen ist sehr gut die Überlagerung von Rotation und Translation zu erkennen. Die Translation wiederum kann man in eine waagrechte Bewegung mit konstantem Impuls und eine senkrechte mit konstanter Impulszunahme zerlegen.
- Zieht der Springer während der Drehung zusammen, so verkleinert er sein Trägheitsmoment. Weil sein Drehimpuls aber unverändert ist, vergrößert sich seine Drehgeschwindigkeit. Beim Öffnen geschieht der umgekehrte Vorgang.
Versuch: Auto und Kiste
- Aufbau
- Beobachtung
Das Auto trifft genau die Kiste!
In diesem Film kann man sich das von der Seite anschauen.
- Interpretation
Versuch: Die fallende Zielscheibe
- Aufbau
Animation Schiefer Wurf
Zweites Newtonsches Gesetz (vektorielle Form)
Bisher wurde die Änderung des Impulses nur längs einer Richtung betrachtet. Dabei wirkt die Kraft parallel oder antiparallel zum Impulsvektor. Die Kraft gibt die zeitliche Änderung des Impulses an.
Auch wenn die Kraft nicht (anti)parallel zum Impuls wirkt, gibt sie die zeitliche Änderung des Impulses an. Dabei ändert sich nicht nur der Betrag, sondern auch die Richtung des Impulses!
Links
- Video von sytemphysik einer genaueren mathematischen Untersuchung der Peltonturbine.
- Pelton Turbine/Wheel Working & Design
- WATER TURBINE PELTON COSTA RICA
- Pelton-Turbine (Aufbau und Funktionsweise) 3D-Animation