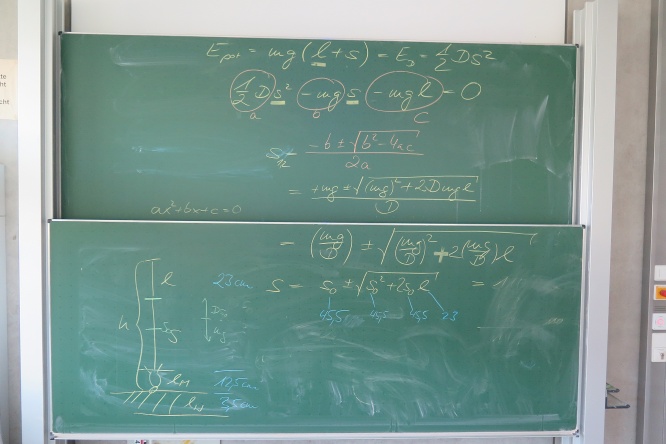Energiebilanzen: Unterschied zwischen den Versionen
(→Energiebilanzen) |
|||
| (11 dazwischenliegende Versionen des gleichen Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | ([[Inhalt_Klasse_10|'''Klassische Mechanik''']] > [[Inhalt_Klasse_10#Energieerhaltung|'''Energieerhaltung''']]) | ||
| + | |||
==Beispiele== | ==Beispiele== | ||
| − | <gallery widths=150px heights=130px perrow=4 | + | <gallery widths=150px heights=130px perrow=4 > |
| − | Bild:[[ | + | Bild:Achterbahn_Colossos.jpg|Welches ist eigentlich die größte Achterbahn der Welt? |
| − | Bild:| | + | Bild:Achterbahn_Blue_Fire.jpg|([[Media:Achterbahnfahrt blue fire.ogg|'''Video''']]) einer Achterbahnfahrt |
| − | + | Bild:Spielzeugpistole_Laden.jpg|Eine Spielzeugpistole wird "geladen". ([[Media:Spielzeugpistole_Laden.ogg|'''Video''']]) Welche Geschwindigkeit erreicht der Pfeil wohl? | |
| − | Bild:| | + | Bild:Springbrunnen_unterschiedliche_Höhen.jpg|([[Media:Springbrunnen_unterschiedliche_Höhen.ogg|'''Video''']]) Warum spritzen denn die Geysire unterschiedlich hoch? |
| − | Bild:| | + | Bild:Bungee jumping Absprung.jpg|Beim Bungee jumping will man... |
| + | Bild:Bungee jumping Eintauchen.jpg|gerade noch ins Wasser eintauchen. | ||
</gallery> | </gallery> | ||
| − | === | + | == Formeln für Energieformen == |
| − | + | ===Lageenergie=== | |
| − | + | Ein 6kg schwerer Koffer wird von Jemandem vom Boden auf einen 1,5 m hohen Tisch angehoben. | |
| − | + | Die dazu benötigte Energie kommt aus dem Menschen und ist dann als Lageenergie gespeichert. | |
| − | + | Dabei spielt es keine Rolle auf welchem Weg dies passiert, ob er senkrecht nach oben gehoben wird oder mit Hilfe einer schiefen Ebene oder mit einer anderen Maschine. Immer ist das Produkt aus wirkender Kraft und Weglänge gleichgroß. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | Beim Hochheben muss man die Gewichtskraft des Koffers ausgleichen, die sich aus der Masse des Koffers und dem Ortsfaktor ergibt: | |
| − | === | + | :<math>F= m\, g = 6\, \rm kg \cdot 10\frac{N}{kg} = 60 \, N</math> |
| − | + | ||
| − | == | + | Die übertragene Energie beträgt daher: |
| − | + | :<math>E=F s = 60\,\rm N \cdot 1{,}5\,m = 90 \, Nm</math> | |
| − | + | {|class="wikitable" style="border-style: solid; border-width: 4px " | |
| + | | | ||
| + | Um einen Gegenstand mit der Masse m auf der Erde um die Höhe h anzuheben benötigt man die Energie: | ||
| + | |||
| + | :<math>E = m\, g\, h</math> | ||
| + | |||
| + | Diese Energiemenge ist als Lageenergie im [[Feldenergie (qualitativ)|Schwerefeld]] gespeichert. | ||
| + | |} | ||
| − | + | ===Bewegungsenergie=== | |
| + | Ein Gegenstand hat viel Bewegungsenergie, wenn er schnell ist, also eine große Geschwindigkeit hat, und er eine große Masse hat. Das trifft auch für den Impuls zu, die Frage ist daher wie genau Geschwindigkeit und Masse mit der Bewegungsenergie zusammenhängen. Es muss auch rechnerisch einen Unterschied zum Impuls geben. | ||
| − | + | Dazu beschleunigt man einen Gegenstand mit einer konstanten Kraft F eine bekannte Zeitdauer t. Je nach Masse m des Gegenstands legt man dazu einen mehr oder weniger langen Weg der Länge s zurück. | |
| + | Danach enthält der Gegenstand dann den Impuls <math>p=F\, t</math>. Um die enthaltene Energie <math>E=F\, s</math> zu berechnen, muss man die Länge der Beschleunigungsstrecke kennen. | ||
| + | [[Datei:Kinematik_Interpretation_v-t-Diagramm_gleichmäßig_beschleunigt.png|thumb]] | ||
| + | Die Weglänge s ergibt sich aus dem Geschwindigkeit-Zeit-Diagrammm der Bewegung: | ||
Die Fläche des Dreiecks entspricht der Wegstrecke s. Nach der Zeit t hat der Gegenstand die Geschwindigkeit v, es gilt also: | Die Fläche des Dreiecks entspricht der Wegstrecke s. Nach der Zeit t hat der Gegenstand die Geschwindigkeit v, es gilt also: | ||
| Zeile 40: | Zeile 50: | ||
::<math>=\frac{1}{2} \, m \, v^2 =\frac{1}{2} \, \frac{p^2}{m}</math> | ::<math>=\frac{1}{2} \, m \, v^2 =\frac{1}{2} \, \frac{p^2}{m}</math> | ||
| + | {|class="wikitable" style="border-style: solid; border-width: 4px " | ||
| + | | | ||
| + | Ein Gegenstand mit der Masse m und dem Impuls p (der Masse m und der Geschwindigkeit v) enthält die Bewegungsenergie | ||
| + | :<math>E_{kin}=\frac{1}{2} \, \frac{p^2}{m}=\frac{1}{2} \, m \, v^2</math> | ||
| − | + | Die Bewegungsenergie ist bei gleicher Geschwindigkeit proportional zur Masse und | |
| − | + | <br>bei gleicher Masse proportional zum Quadrat des Impulses (der Geschwindigkeit). | |
| − | + | |} | |
| − | + | ||
| − | + | ||
===Spannenergie=== | ===Spannenergie=== | ||
Wieviel Energie steckt in einer Feder, die um die Strecke s gedehnt wurde? Außer von der Auslenkung hängt dies bestimmt von ihrer Härte ab, die man mit der Federkonstante D in N/m beschreiben kann. | Wieviel Energie steckt in einer Feder, die um die Strecke s gedehnt wurde? Außer von der Auslenkung hängt dies bestimmt von ihrer Härte ab, die man mit der Federkonstante D in N/m beschreiben kann. | ||
| − | Bei der Verlängerung der Feder ist die Kraft nicht konstant, sondern steigt linear an. Je größer die Auslenkung, desto mehr Energie benötigt man, um noch einen weiteren Zentimeter zu dehnen | + | Bei der Verlängerung der Feder ist die Kraft nicht konstant, sondern steigt linear an. Je größer die Auslenkung, desto mehr Energie benötigt man, um noch einen weiteren Zentimeter zu dehnen. Um weiterhin mit der Formel "Kraft * Weg" arbeiten zu könne, muss man mit einer mittleren Kraft rechnen! |
Wie auch bei der Verallgemeinerung der Impulsmenge P = F t kann man auch hier das Problem mit einer Fläche in einem Diagramm lösen. Die Energiemenge entspricht im Kraft-Weg-Diagramm der Fläche zwischen Graphen und s-Achse. | Wie auch bei der Verallgemeinerung der Impulsmenge P = F t kann man auch hier das Problem mit einer Fläche in einem Diagramm lösen. Die Energiemenge entspricht im Kraft-Weg-Diagramm der Fläche zwischen Graphen und s-Achse. | ||
| Zeile 60: | Zeile 72: | ||
Allgemein gilt, dass die Kraft linear mit der Verlängerung zunimmt, je nach Federhärte D mehr oder weniger stark. Die maximale Kraft erreicht man bei maximaler Auslenkung: F = D s. Die Dreiecksfläche beträgt also: | Allgemein gilt, dass die Kraft linear mit der Verlängerung zunimmt, je nach Federhärte D mehr oder weniger stark. Die maximale Kraft erreicht man bei maximaler Auslenkung: F = D s. Die Dreiecksfläche beträgt also: | ||
| − | :<math>E = \frac{1}{2}\, F \, s = \frac{1}{2}\, D \, s^2</math> | + | :<math>E = \frac{1}{2}\, F \, s = \frac{1}{2}\, D \, s\, s = \frac{1}{2}\, D \, s^2</math> |
| − | + | {|class="wikitable" style="border-style: solid; border-width: 4px " | |
| − | + | | | |
| − | + | Eine Feder mit der Federkonstante D, die um die Strecke s verlängert wurde, enthält die | |
| + | Spannenergie | ||
| + | :<math>E_{sp} = \frac{1}{2}\, D \, s^2</math> | ||
| + | |||
| + | Die Spannergie ist proportional zum Quadrat der Verlängerung. | ||
| + | |||
| + | |} | ||
== Energiemengen im Weg-Kraft-Diagramm == | == Energiemengen im Weg-Kraft-Diagramm == | ||
| Zeile 81: | Zeile 99: | ||
* Es gilt, wie überall die Energieerhaltung | * Es gilt, wie überall die Energieerhaltung | ||
* Energiebilanzen Achterbahn, Pendel, etc | * Energiebilanzen Achterbahn, Pendel, etc | ||
| + | |||
| + | ==Versuch: Bungee Jumping== | ||
| + | ;Aufbau | ||
| + | <gallery widths=180px heights=120px perrow=4> | ||
| + | Bild:Bungee-Jumping Versuchsaufbau.jpg|Der Versuchsaufbau | ||
| + | Bild:Bungee-Jumping Versuchsaufbau Person.jpg|Die Person und das Gewicht sind mit Knete befestigt. | ||
| + | </gallery> | ||
| + | An einer Feder hängt eine mit einem Gewicht beschwerte Spielzeug-Figur. Darunter eine wassergefüllte Kiste. | ||
| + | Die Person steht zu Beginn oben am Anfang der Feder und läßt sich dann fallen. | ||
| + | |||
| + | Wie hoch muß man den Anfang der Feder befestigen, damit die Person das Wasser gerade berührt? | ||
| + | |||
| + | ;Rechnung | ||
| + | [[Datei:Bungee-Jumping_Rechnung_klein.jpg|666px]] | ||
Aktuelle Version vom 21. Juli 2017, 10:00 Uhr
(Klassische Mechanik > Energieerhaltung)
Inhaltsverzeichnis
Beispiele
(Video) einer Achterbahnfahrt
Eine Spielzeugpistole wird "geladen". (Video) Welche Geschwindigkeit erreicht der Pfeil wohl?
(Video) Warum spritzen denn die Geysire unterschiedlich hoch?
Formeln für Energieformen
Lageenergie
Ein 6kg schwerer Koffer wird von Jemandem vom Boden auf einen 1,5 m hohen Tisch angehoben.
Die dazu benötigte Energie kommt aus dem Menschen und ist dann als Lageenergie gespeichert.
Dabei spielt es keine Rolle auf welchem Weg dies passiert, ob er senkrecht nach oben gehoben wird oder mit Hilfe einer schiefen Ebene oder mit einer anderen Maschine. Immer ist das Produkt aus wirkender Kraft und Weglänge gleichgroß.
Beim Hochheben muss man die Gewichtskraft des Koffers ausgleichen, die sich aus der Masse des Koffers und dem Ortsfaktor ergibt:
- [math]F= m\, g = 6\, \rm kg \cdot 10\frac{N}{kg} = 60 \, N[/math]
Die übertragene Energie beträgt daher:
- [math]E=F s = 60\,\rm N \cdot 1{,}5\,m = 90 \, Nm[/math]
|
Um einen Gegenstand mit der Masse m auf der Erde um die Höhe h anzuheben benötigt man die Energie:
Diese Energiemenge ist als Lageenergie im Schwerefeld gespeichert. |
Bewegungsenergie
Ein Gegenstand hat viel Bewegungsenergie, wenn er schnell ist, also eine große Geschwindigkeit hat, und er eine große Masse hat. Das trifft auch für den Impuls zu, die Frage ist daher wie genau Geschwindigkeit und Masse mit der Bewegungsenergie zusammenhängen. Es muss auch rechnerisch einen Unterschied zum Impuls geben.
Dazu beschleunigt man einen Gegenstand mit einer konstanten Kraft F eine bekannte Zeitdauer t. Je nach Masse m des Gegenstands legt man dazu einen mehr oder weniger langen Weg der Länge s zurück.
Danach enthält der Gegenstand dann den Impuls [math]p=F\, t[/math]. Um die enthaltene Energie [math]E=F\, s[/math] zu berechnen, muss man die Länge der Beschleunigungsstrecke kennen.
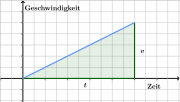
Die Weglänge s ergibt sich aus dem Geschwindigkeit-Zeit-Diagrammm der Bewegung:
Die Fläche des Dreiecks entspricht der Wegstrecke s. Nach der Zeit t hat der Gegenstand die Geschwindigkeit v, es gilt also:
- [math]s= \frac{1}{2}\, v\, t[/math]
Mit der Impulsmenge [math]p = F\, t =m \, v[/math] folgt daraus für die Energie:
- [math]E = F\, s = F \, \frac{1}{2}\, v\, t =\frac{1}{2} \, p \, v [/math]
- [math]=\frac{1}{2} \, m \, v^2 =\frac{1}{2} \, \frac{p^2}{m}[/math]
|
Ein Gegenstand mit der Masse m und dem Impuls p (der Masse m und der Geschwindigkeit v) enthält die Bewegungsenergie
Die Bewegungsenergie ist bei gleicher Geschwindigkeit proportional zur Masse und
|
Spannenergie
Wieviel Energie steckt in einer Feder, die um die Strecke s gedehnt wurde? Außer von der Auslenkung hängt dies bestimmt von ihrer Härte ab, die man mit der Federkonstante D in N/m beschreiben kann.
Bei der Verlängerung der Feder ist die Kraft nicht konstant, sondern steigt linear an. Je größer die Auslenkung, desto mehr Energie benötigt man, um noch einen weiteren Zentimeter zu dehnen. Um weiterhin mit der Formel "Kraft * Weg" arbeiten zu könne, muss man mit einer mittleren Kraft rechnen!
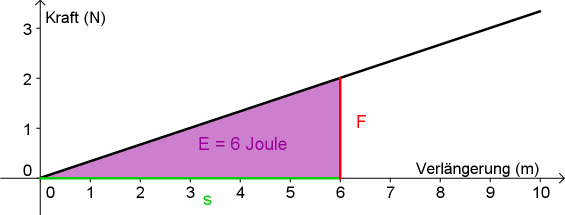
Wie auch bei der Verallgemeinerung der Impulsmenge P = F t kann man auch hier das Problem mit einer Fläche in einem Diagramm lösen. Die Energiemenge entspricht im Kraft-Weg-Diagramm der Fläche zwischen Graphen und s-Achse.
In diesem Beispiel beträgt die Federhärte 0,5 Newton pro Meter und die Feder wurde um 6 Meter gedehnt. Dabei wurde Energie von 6 Joule auf die Feder übertragen. (Die Zahlenangaben sind unrealistisch. Normalerweise liegen Federhärten im Bereich ab 10 N/m für sehr weiche Federn.)
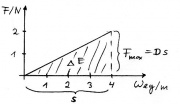
Allgemein gilt, dass die Kraft linear mit der Verlängerung zunimmt, je nach Federhärte D mehr oder weniger stark. Die maximale Kraft erreicht man bei maximaler Auslenkung: F = D s. Die Dreiecksfläche beträgt also:
- [math]E = \frac{1}{2}\, F \, s = \frac{1}{2}\, D \, s\, s = \frac{1}{2}\, D \, s^2[/math]
|
Eine Feder mit der Federkonstante D, die um die Strecke s verlängert wurde, enthält die Spannenergie
Die Spannergie ist proportional zum Quadrat der Verlängerung. |
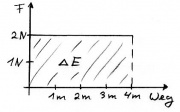
Energiemengen im Weg-Kraft-Diagramm
s-F-Diagramm Fläche ist Energiemenge. Bei konstanter Kraft: E=Fs
Energiebilanzen
- Es gilt, wie überall die Energieerhaltung
- Energiebilanzen Achterbahn, Pendel, etc
Versuch: Bungee Jumping
- Aufbau
An einer Feder hängt eine mit einem Gewicht beschwerte Spielzeug-Figur. Darunter eine wassergefüllte Kiste. Die Person steht zu Beginn oben am Anfang der Feder und läßt sich dann fallen.
Wie hoch muß man den Anfang der Feder befestigen, damit die Person das Wasser gerade berührt?
- Rechnung