Geschwindigkeits- und Beschleunigungsdiagramme von Bewegungen: Unterschied zwischen den Versionen
| (6 dazwischenliegende Versionen des gleichen Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | ([[Inhalt_Klasse_10|'''Klassische Mechanik''']] > [[Inhalt_Klasse_10#Kinematik_-_.22Ja.2C_wo_laufen_sie_denn.3F.22|'''Kinematik''']]) | ||
| + | |||
<gallery widths=150px heights=130px perrow=4 > | <gallery widths=150px heights=130px perrow=4 > | ||
Bild:Tachoscheibe.jpg|Die Tachoscheibe eines LKWs. | Bild:Tachoscheibe.jpg|Die Tachoscheibe eines LKWs. | ||
| − | Bild:Verkehrsunfalluntersuchung_klein.jpg|Wer war Schuld? ([http://www.unfallaufnahme.info/unfallspuren/ | + | Bild:Verkehrsunfalluntersuchung_klein.jpg|Wer war Schuld? ([http://www.unfallaufnahme.info/content/unfallspuren/uebersicht_unfallspuren/ Verschiedene Unfallspuren]) |
| − | Bild:Bremsspuren_Autobahn.jpg|War der Sicherheitsabstand ausreichend? ([http://www.unfallaufnahme.info/uebersichten-listen-und-tabellen/geschwindigkeiten-und-bremswege/ | + | Bild:Bremsspuren_Autobahn.jpg|War der Sicherheitsabstand ausreichend? ([http://www.unfallaufnahme.info/content/uebersichten-listen-und-tabellen/geschwindigkeiten-und-bremswege/ Bremsverzögerungswerte auf verschiedenem Untergrund]) |
Bild:Bremsspur_Unfall_Baum.jpg|Wurde hier die Höchstgeschwindigkeit überschritten? | Bild:Bremsspur_Unfall_Baum.jpg|Wurde hier die Höchstgeschwindigkeit überschritten? | ||
</gallery> | </gallery> | ||
| Zeile 37: | Zeile 39: | ||
:<math>a=\frac{0{,}4\rm\frac{m}{sec}}{2{,5}\rm s} = 0{,}16\rm \frac{m}{s^2}</math> | :<math>a=\frac{0{,}4\rm\frac{m}{sec}}{2{,5}\rm s} = 0{,}16\rm \frac{m}{s^2}</math> | ||
| − | :Das Abbremsen ging viel schneller als das Beschleunigen. Innerhalb von nur 0,2s fiel die Geschwindigkeit um 0,4m/sec. | + | :Das Abbremsen ging viel schneller als das Beschleunigen. Innerhalb von nur 0,2s fiel die Geschwindigkeit um 0,4m/sec. Außerdem war die Beschleunigung beim Bremsen nicht konstant. Die mittlere Beschleunigung betrug |
:<math>\bar a=\frac{-0{,}4\rm\frac{m}{s}}{0{,}2\rm s} = -2\rm \frac{m}{s^2}</math> | :<math>\bar a=\frac{-0{,}4\rm\frac{m}{s}}{0{,}2\rm s} = -2\rm \frac{m}{s^2}</math> | ||
| Zeile 60: | Zeile 62: | ||
=== Flächen in Diagrammen === | === Flächen in Diagrammen === | ||
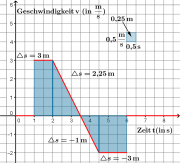
| − | [[Bild: | + | [[Bild:Ortsänderung_als_Fläche_unter_der_Geschwindigkeitskurve_Beschleunigung_konstant.png|thumb|Der Wagen steht zunächst. Dann fährt er 5,25m, kehrt um, fährt 4m zurück und bleibt stehen.]] |
Die Flächen zwischen dem Schaubild und der Zeitachse lassen sich anschaulich interpretieren. Grundlage dazu ist der sogenannte Hauptsatz der Differential-Integralrechnung (HDI), den man in Worten so formulieren kann: | Die Flächen zwischen dem Schaubild und der Zeitachse lassen sich anschaulich interpretieren. Grundlage dazu ist der sogenannte Hauptsatz der Differential-Integralrechnung (HDI), den man in Worten so formulieren kann: | ||
| Zeile 76: | Zeile 78: | ||
* Die Fläche unterhalb des Beschleunigungs-Schaubildes entspricht der Geschwindigkeitsänderung. | * Die Fläche unterhalb des Beschleunigungs-Schaubildes entspricht der Geschwindigkeitsänderung. | ||
| − | |||
==Links== | ==Links== | ||
| − | *[http://www.unfallaufnahme.info | + | *[http://www.unfallaufnahme.info Polizeiliche Verkehrsunfallaufnahme] (Ein Polizeibeamter gibt seine langjährigen Erfahrungen weiter. Es geht um Unfallspuren, Unfallfotografie und Photogrammetrie.) |
Aktuelle Version vom 26. Mai 2017, 08:59 Uhr
(Klassische Mechanik > Kinematik)
Wer war Schuld? (Verschiedene Unfallspuren)
War der Sicherheitsabstand ausreichend? (Bremsverzögerungswerte auf verschiedenem Untergrund)
Inhaltsverzeichnis
Beispiele und Versuche
Skateboard fahren
- Aufbau
Jemand stellt sich auf ein Skateboard und stößt sich einmal kurz vom Boden ab. Mit einem Ultraschallsensor wird 25 in der Sekunde der Ort der Person gemessen.
- Messung
- Auswertung
Beim Abstoßen steigt die Geschwindigkeit schnell an. Danach rollt die Person aus, die Geschwindigkeit nimmt dabei gleichmäßig ab.
Ein Wagen rollt bergab
- Aufbau
Ein kleiner Wagen wird auf eine schräggestellte Schiene gesetzt und losgelassen. Am Ende der Schiene bremst etwas Knete den Wagen.
Mit Hilfe eines Ultraschallsensors kann dabei der Ort des Wagens bestimmt werden, wobei das Ortskoordinatensystem gerade die Schiene selbst ist. Den Nullpunkt kann man beliebig setzen, z.B. an den linken Rand der Schiene.
- Messung
- Auswertung
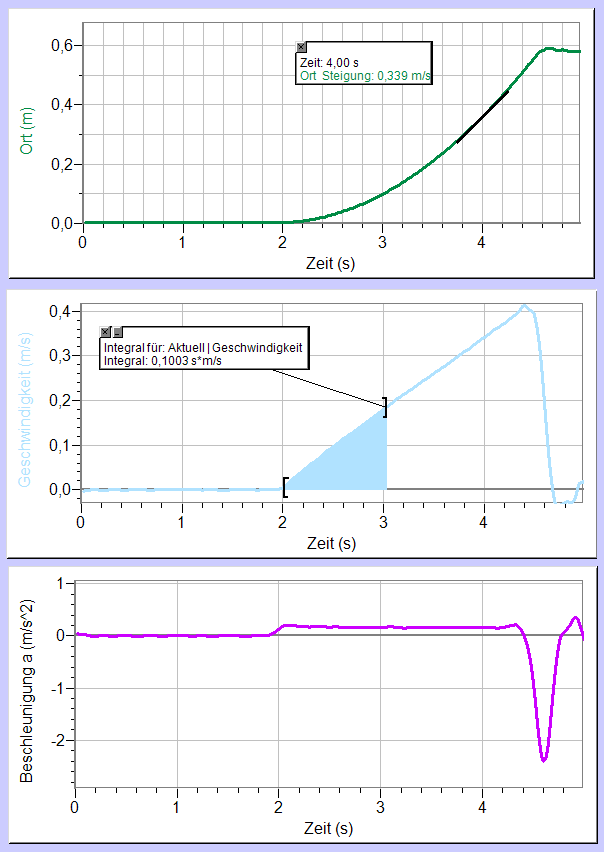
Am Ortsdiagramm kann man folgendes ablesen:
- Der Wagen befindet sich zunächst am Anfang der Schiene. Nach ca. zwei Sekunden wurde er losgelassen und erreicht den Knetklumpen nach ca. 4,5 Sekunden. Während seiner Fahrt wurde er immer schneller. Der Knetklumpen lag 0,6m vom linken Rand entfernt.
Das Geschwindigkeitsdiagramm liefert folgendes:
- Die Geschwindigkeit hat gleichmäßig zugenommen. Innerhalb von 2,5s um 0,4 m/s.
- Die Beschleunigung beim Bergabrollen war also in etwa konstant. Sie beträgt
- [math]a=\frac{0{,}4\rm\frac{m}{sec}}{2{,5}\rm s} = 0{,}16\rm \frac{m}{s^2}[/math]
- Das Abbremsen ging viel schneller als das Beschleunigen. Innerhalb von nur 0,2s fiel die Geschwindigkeit um 0,4m/sec. Außerdem war die Beschleunigung beim Bremsen nicht konstant. Die mittlere Beschleunigung betrug
- [math]\bar a=\frac{-0{,}4\rm\frac{m}{s}}{0{,}2\rm s} = -2\rm \frac{m}{s^2}[/math]
Das Beschleunigungsdiagamm bestätigt die am Geschwindigkeitsdiagramm gefundenen Aussagen.
Beschreibung einer Bewegung
Wie schnell ist der Gegenstand?
Die Geschwindigkeit ist die zeitliche Änderung des Ortes. ([math]\dot s[/math]) Bei einer eindimensionalen Bewegung wird die Richtung entgegen dem Koordinatensystem mit einem negativen Vorzeichen ausgedrückt. In der Fläche und im Raum ist die Geschwindigkeit eine vektorielle Größe und wird als [math]\vec v[/math] notiert.
Bremst/beschleunigt der Gegenstand?
Die Beschleunigung ist die zeitliche Änderung der Geschwindigkeit. [math]a = \dot v[/math] Im eindimensionalen gibt ein negatives Vorzeichen die Verringerung der Geschwindigkeit, also einen Bremsvorgang an. In der Fläche und im Raum ist sie auch eine vektorielle Größe und wird [math]\vec a[/math] geschrieben.
Beschreibung des zeitlichen Verlaufs
Wann ist der Körper wie schnell?
Ordnet man jedem Zeitpunkt der momentanen Geschwindigkeit zu, so erhält man das Geschwindigkeitsgesetz [math]v(t)[/math]. Das Schaubild heißt Geschwindigkeit-Zeit-Diagramm.
- Die Steigung einer Tangente im Geschwindigkeit-Zeit-Diagramm ist die momentane Beschleunigung [math]a=\dot v[/math],
- die Sekantensteigung ist die mittlere Beschleunigung [math]\bar a= \frac{\Delta v}{\Delta t}[/math]
Flächen in Diagrammen
Die Flächen zwischen dem Schaubild und der Zeitachse lassen sich anschaulich interpretieren. Grundlage dazu ist der sogenannte Hauptsatz der Differential-Integralrechnung (HDI), den man in Worten so formulieren kann:
Das Integral (die Fläche) unterhalb der Änderungsrate ergibt die Gesamtänderung. Dabei werden Flächen unterhalb der x-Achse negativ gewertet.
Trägt man z.B. die zeitliche Änderungsrate des Ortes (die Geschwindigkeit) über der Zeit auf, so entspricht die Fläche unterhalb des Schaubildes der Gesamtänderung des Ortes.
[math]\Delta s = s_2-s_1 = \int_{t_1}^{t_2} v(t) \ \mathrm{dt}[/math]
Mit Hilfe des GTRs kann man Flächen unter Schaubildern numerisch bestimmen. (Genauere Beschreibung unter Berechnung von Energiemengen.)
Für die Beschreibung von Bewegungen bedeutet das:
- Die Fläche unterhalb des Geschwindigkeit-Schaubildes entspricht der Ortsänderung, also der zurückgelegten Strecke.
- Die Fläche unterhalb des Beschleunigungs-Schaubildes entspricht der Geschwindigkeitsänderung.
Links
- Polizeiliche Verkehrsunfallaufnahme (Ein Polizeibeamter gibt seine langjährigen Erfahrungen weiter. Es geht um Unfallspuren, Unfallfotografie und Photogrammetrie.)