Bewegung im Raum - Vektorielle Geschwindigkeit: Unterschied zwischen den Versionen
(→2) Über den Fluss) |
(→Zerlegung einer Geschwindigkeit in Komponenten) |
||
| (25 dazwischenliegende Versionen des gleichen Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | ([[Inhalt_Klasse_10|'''Klassische Mechanik''']] > [[Inhalt_Klasse_10#Kinematik_-_.22Ja.2C_wo_laufen_sie_denn.3F.22|'''Kinematik''']]) | ||
| + | |||
<gallery widths=250px heights=200px perrow=2 > | <gallery widths=250px heights=200px perrow=2 > | ||
Bild:Rolltreppe.jpg|Wie schnell bewegen sich die Personen? <br/> ([[Media:Rolltreppe.ogg|Video anschauen]]) | Bild:Rolltreppe.jpg|Wie schnell bewegen sich die Personen? <br/> ([[Media:Rolltreppe.ogg|Video anschauen]]) | ||
| − | Bild:Flugzeug_Landung_Seitenwind_Vorhaltewinkel.jpg|Ob dieses Flugzeug heil runter kommt? <br/>([http://www.youtube.com/watch?v=ihEmw9CPvJU Video anschauen | + | Bild:Flugzeug_Landung_Seitenwind_Vorhaltewinkel.jpg|Ob dieses Flugzeug heil runter kommt? <br/>([http://www.youtube.com/watch?v=ihEmw9CPvJU Video anschauen]) <br/> ([http://www.youtube.com/watch?v=TCUHQ_-l6Qg Video: Landende B52]) |
| − | Bild:Applet_relativeVelocity.gif|Wie schnell ist das fahrende Schiff? ([http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=140.0 Applet]) | + | Bild:Applet_relativeVelocity.gif|Wie schnell ist das fahrende Schiff? ([http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=140.0 JAVA-Applet]) <br>([https://www.daserste.de/information/wissen-kultur/kopfball/videosextern/pfeil-aus-auto-abschiessen-108.html Video: Pfeil aus Auto abschießen]) |
| − | Bild:Applet_Boat_and_River.png|Wie ein Boot über den Fluss fährt. ([http://www.surendranath.org | + | Bild:Applet_Boat_and_River.png|Wie ein Boot über den Fluss fährt. ([http://www.surendranath.org Animation: Menü>Kinematics>Boat&River]) |
</gallery> | </gallery> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | == | + | ==Versuch: Flussüberquerung== |
| − | === | + | ;Aufbau |
| − | + | <gallery widths=150px heights=130px perrow=4 > | |
| − | : | + | Bild:Geschwindigkeit Überlagerung Vektor Fluss Versuchsaufbau gesamt.jpg |
| − | + | Bild:Geschwindigkeit Überlagerung Vektor Fluss Versuchsaufbau Antrieb.jpg | |
| + | Bild:Geschwindigkeit Überlagerung Vektor Fluss Versuchsaufbau Papierrolle.jpg | ||
| + | </gallery> | ||
| − | == | + | ==Geschwindigkeit als vektorielle Größe== |
| − | + | Beschreibt man die Geschwindigkeit eines bewegten Gegenstandes, so muss man angeben wie schnell er ist und in welche Richtung er sich bewegt. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | Gibt es nur zwei mögliche Richtungen, wie Oben/Unten oder Links/Rechts, so kann man von positiven und negativen Geschwindigkeit sprechen. Kann die Bewegung in irgendeiner Richtung verlaufen, so beschreibt man die Geschwindigkeit mit einem Pfeil (oder auch "Vektor"). Der Pfeil zeigt in Richtung der Bewegung, seine Länge gibt den Betrag der Geschwindigkeit an. | |
| − | + | ||
| − | Die | + | Einen Vektor benennt man mit einem "gepfeilten" Buchstaben, ohne den Pfeil ist die Länge des Vektors gemeint: |
| − | + | ||
| − | : | + | <gallery widths=200px heights=150px perrow=4> |
| − | + | Bild:Geschwindigkeit_vektoriell_Lokomotive.jpg|Die Lokomotive kann nur vorwärts und rückwärts fahren. | |
| − | : | + | Bild:Geschwindigkeit_vektoriell_Fußgänger_Vogelperspektive.jpg|Die Fußgänger können sich in der Ebene bewegen. |
| + | Bild:Geschwindigkeit_vektoriell_Flugzeug_Abflug.jpg|Das Flugzeug bewegt sich in drei Dimensionen. | ||
| + | </gallery> | ||
| + | |||
| + | ==Addition (Überlagerung) von Geschwindigkeiten== | ||
| + | Geschwindigkeiten kann man mit einem Pfeildiagramm vektoriell addieren. Die resultierende Geschwindigkeit erhält man durch Aneinanderlegen der Pfeile oder durch ein "Vektorparallelogramm". | ||
| + | |||
| + | Bei (anti)parallelen Geschwindigkeiten könnte man statt mit Vektoren auch mit positiven und negativem Vorzeichen arbeiten. | ||
| + | <br>Dementsprechend kann man Geschwindigkeiten auch subtrahieren. | ||
| + | |||
| + | <gallery widths=227px heights=330px perrow=3 caption="Ein Boot fährt auf einem Fluss"> | ||
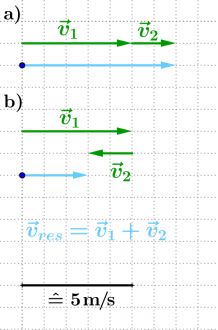
| + | Bild:Geschwindigkeit vektoriell Pfeildiagramme eindimensional.png|Der Fluss fließt mit der Geschwindigkeit <math>v_1 = 5\,\rm m/s </math> nach rechts. <br/> Das Boot fährt mit <math>v_2 = 2\,\rm m/s </math> <br/> a) nach rechts: <math>|\vec v_{res}| = v_{res} = 3\,\rm m/s</math> <br/> b) nach links: <math>|\vec v_{res}| = v_{res} = 7\,\rm m/s</math> | ||
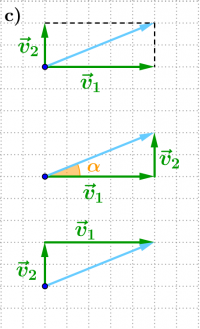
| + | Bild:Geschwindigkeit vektoriell Pfeildiagramme rechtwinklig.png|Der Fluss fließt mit der Geschwindigkeit <math>v_1 = 5\,\rm m/s </math> nach rechts: <br/> c) Das Boot fährt mit <math>v_2 = 2\,\rm m/s </math> rechtwinklig zur Flussrichtung. <br/> <math>|\vec v_{res}| = v_{res} \approx 5{,}4\,\rm m/s</math> <br/> <math>\alpha = 21{,}8^\circ</math> | ||
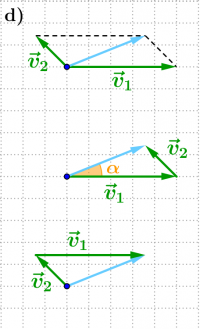
| + | Bild:Geschwindigkeit vektoriell Pfeildiagramme schiefwinklig.png|Der Fluss fließt mit der Geschwindigkeit <math>v_1 = 5\,\rm m/s </math> nach rechts: <br/> d) Das Boot fährt mit <math>v_2 = 2\,\rm m/s </math> im Winkel von 45° schräg nach links: <br/> <math>|\vec v_{res}| = v_{res} \approx 3{,}9\,\rm m/s</math> <br/> <math>\alpha = 21{,}5^\circ</math> | ||
| + | </gallery> | ||
| + | |||
| + | ==Zerlegung einer Geschwindigkeit in Komponenten== | ||
| + | Die Geschwindigkeit eines Flugzeugs im Raum kann man in Komponenten zerlegen: In x-, y- und z-Richtung. | ||
| + | <br>Dieses Flugzeug steigt und sinkt aber nicht und es genügt die Komponenten in Ost-West-Richtung (x-Komponente) und Nord-Südrichtung (y-Komponente) zu betrachten. | ||
| + | |||
| + | An dem blauen Punkt kann man die Geschwindigkeit des Flugzeugs verändern. | ||
| + | |||
| + | {{#widget:Iframe | ||
| + | |url=https://www.geogebra.org/material/iframe/id/vgzys3vr/width/530/height/400/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/true/rc/false/ld/false/sdz/false/ctl/false | ||
| + | |width=530 | ||
| + | |height=400 | ||
| + | |border=0 | ||
| + | }} | ||
| + | |||
| + | (Zur [https://www.geogebra.org/material/show/id/de7pFAdR Datei] und zum [https://www.geogebra.org/download?lang=de Programm]) | ||
| + | |||
| + | ==[[Aufgaben_zur_Kinematik_(Bewegungslehre)#Vektorielle_Geschwindigkeiten|Aufgaben]]== | ||
==[[Aufgaben zur Geschwindigkeit als Vektor - Lösungen|Lösungen]]== | ==[[Aufgaben zur Geschwindigkeit als Vektor - Lösungen|Lösungen]]== | ||
| + | |||
| + | ==Links== | ||
| + | *[https://lehrerfortbildung-bw.de/u_matnatech/physik/gym/bp2004/fb3/modul3/4_material_geschw/ue/ Unterrichtsgang vektorielle Geschwindigkeit] (Materialiensammlung des Lehrerfortbildungsservers Baden-Württemberg) | ||
| + | |||
| + | *Video: [https://www.daserste.de/information/wissen-kultur/kopfball/videosextern/pfeil-aus-auto-abschiessen-108.html Pfeil aus Auto abschießen] ARD Kopfball, vom 10.01.2015 ([http://www.buckle-up.de/de/projects.php?we_objectID=101 Wie verhält sich ein Pfeil, wenn man ihn aus einem fahrenden Auto abschießt?] Buckle-up Productions GbR, Velbert) | ||
| + | |||
| + | *Video: [http://www.youtube.com/watch?v=ihEmw9CPvJU Awkward crosswind landings 2013] von "flugsnug", youtube | ||
| + | |||
| + | **Video: [http://www.youtube.com/watch?v=TCUHQ_-l6Qg Landende B52 bei Seitenwind] von "peter greenwood", youtube | ||
| + | |||
| + | *Java-Applet: [http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=140.0 Relative Motion (frame of reference)] von Fu-Kwun Hwang, NTNUJAVA Virtual Physics Laboratory | ||
| + | |||
| + | **Applet: [http://www.surendranath.org Boat Crossing a River] (Menü>Kinematics>Boat&River) von B.Surendranath, Hyderabad, India | ||
Aktuelle Version vom 10. August 2025, 22:11 Uhr
(Klassische Mechanik > Kinematik)
Wie schnell bewegen sich die Personen?
(Video anschauen)Ob dieses Flugzeug heil runter kommt?
(Video anschauen)
(Video: Landende B52)Wie schnell ist das fahrende Schiff? (JAVA-Applet)
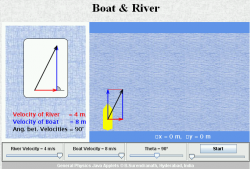
(Video: Pfeil aus Auto abschießen)Wie ein Boot über den Fluss fährt. (Animation: Menü>Kinematics>Boat&River)
Inhaltsverzeichnis
Versuch: Flussüberquerung
- Aufbau
Geschwindigkeit als vektorielle Größe
Beschreibt man die Geschwindigkeit eines bewegten Gegenstandes, so muss man angeben wie schnell er ist und in welche Richtung er sich bewegt.
Gibt es nur zwei mögliche Richtungen, wie Oben/Unten oder Links/Rechts, so kann man von positiven und negativen Geschwindigkeit sprechen. Kann die Bewegung in irgendeiner Richtung verlaufen, so beschreibt man die Geschwindigkeit mit einem Pfeil (oder auch "Vektor"). Der Pfeil zeigt in Richtung der Bewegung, seine Länge gibt den Betrag der Geschwindigkeit an.
Einen Vektor benennt man mit einem "gepfeilten" Buchstaben, ohne den Pfeil ist die Länge des Vektors gemeint:
Addition (Überlagerung) von Geschwindigkeiten
Geschwindigkeiten kann man mit einem Pfeildiagramm vektoriell addieren. Die resultierende Geschwindigkeit erhält man durch Aneinanderlegen der Pfeile oder durch ein "Vektorparallelogramm".
Bei (anti)parallelen Geschwindigkeiten könnte man statt mit Vektoren auch mit positiven und negativem Vorzeichen arbeiten.
Dementsprechend kann man Geschwindigkeiten auch subtrahieren.
- Ein Boot fährt auf einem Fluss
Zerlegung einer Geschwindigkeit in Komponenten
Die Geschwindigkeit eines Flugzeugs im Raum kann man in Komponenten zerlegen: In x-, y- und z-Richtung.
Dieses Flugzeug steigt und sinkt aber nicht und es genügt die Komponenten in Ost-West-Richtung (x-Komponente) und Nord-Südrichtung (y-Komponente) zu betrachten.
An dem blauen Punkt kann man die Geschwindigkeit des Flugzeugs verändern.
Aufgaben
Lösungen
Links
- Unterrichtsgang vektorielle Geschwindigkeit (Materialiensammlung des Lehrerfortbildungsservers Baden-Württemberg)
- Video: Pfeil aus Auto abschießen ARD Kopfball, vom 10.01.2015 (Wie verhält sich ein Pfeil, wenn man ihn aus einem fahrenden Auto abschießt? Buckle-up Productions GbR, Velbert)
- Video: Awkward crosswind landings 2013 von "flugsnug", youtube
- Video: Landende B52 bei Seitenwind von "peter greenwood", youtube
- Java-Applet: Relative Motion (frame of reference) von Fu-Kwun Hwang, NTNUJAVA Virtual Physics Laboratory
- Applet: Boat Crossing a River (Menü>Kinematics>Boat&River) von B.Surendranath, Hyderabad, India