Bewegungsdiagramme und Bewegungsgesetze beliebiger Bewegungen: Unterschied zwischen den Versionen
(→Herleitung / Beispiele / Aufgaben ZU ÜBERARBEITEN!!!) |
|||
| (9 dazwischenliegende Versionen des gleichen Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | ([[Inhalt_Klasse_10|'''Klassische Mechanik''']] > [[Inhalt_Klasse_10#Kräfte_ändern_den_Impuls|'''Kräfte ändern den Impuls''']]) | ||
| + | |||
==Beispiele== | ==Beispiele== | ||
| Zeile 4: | Zeile 6: | ||
Die Kraft ist die zeitliche Änderungsrate des Impulses ("Ableitung der Impulsmenge nach der Zeit"). | Die Kraft ist die zeitliche Änderungsrate des Impulses ("Ableitung der Impulsmenge nach der Zeit"). | ||
| − | ==Herleitung / Beispiele / Aufgaben ZU ÜBERARBEITEN | + | ==Herleitung / Beispiele / Aufgaben (ZU ÜBERARBEITEN)== |
Die folgenden Aufgaben kann man mit dieser [[Animation: Der Kraftverlauf bestimmt die Bewegung (Bewegungsdiagramme)|Animation der Bewegungsdiagramme]] lösen! | Die folgenden Aufgaben kann man mit dieser [[Animation: Der Kraftverlauf bestimmt die Bewegung (Bewegungsdiagramme)|Animation der Bewegungsdiagramme]] lösen! | ||
| Zeile 60: | Zeile 62: | ||
Der braune Schieberegler kann Elisabeth eine Diät verordnen oder sie wieder aufpäppeln. | Der braune Schieberegler kann Elisabeth eine Diät verordnen oder sie wieder aufpäppeln. | ||
| + | |||
| + | |||
| + | Mit der Geogebra-Datei läuft die Animation flüssiger. Hier der Link zur [https://www.geogebra.org/material/show/id/RuzFdebD Datei] (Endung .ggb) und zum [https://www.geogebra.org/download?lang=de Programm]. | ||
| + | |||
{{#widget:Iframe | {{#widget:Iframe | ||
| − | |url=https:// | + | |url=https://www.geogebra.org/material/iframe/id/RuzFdebD/width/926/height/1179/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/false/rc/false/ld/false/sdz/false/ctl/false |
|width=617 | |width=617 | ||
|height=786 | |height=786 | ||
Aktuelle Version vom 8. August 2025, 07:59 Uhr
(Klassische Mechanik > Kräfte ändern den Impuls)
Inhaltsverzeichnis
Beispiele
Allgemeine Formulierung des 2. Newtonschen Gesetzes
Die Kraft ist die zeitliche Änderungsrate des Impulses ("Ableitung der Impulsmenge nach der Zeit").
Herleitung / Beispiele / Aufgaben (ZU ÜBERARBEITEN)
Die folgenden Aufgaben kann man mit dieser Animation der Bewegungsdiagramme lösen!
Pauline und Paul fahren Skateboard. Pauline ist kleiner und bringt deshalb nur 50kg auf die Waage im Vergleich zu doppelt so schweren Paul.
1) Pauline steht zu Beginn am Baum. Dann stößt sie sich anderthalb Sekunden lang mit 40 Newton ab und rollt weiter.
- Vernachläßige zunächst die auftretende Reibung.
- a) Stelle den Kraftverlauf und die Werte von v(0), s(0) und m so ein, dass es der beschriebenen Bewegung entspricht.
- b) Wieviel Impuls hat Pauline nach dem Abstoßen?
- c) Wie schnell ist sie nach dem Abstoßen?
- d) Wie weit fährt sie während des Abstoßens und wie weit in den nächsten viereinhalb Sekunden?
- e) Paul macht nun genau das gleiche wie Pauline: Er steht am Baum und stößt sich anderthalb Sekunden lang mit 40 Newton ab. Vergleiche seine Fahrt mit der von Pauline.
- f) Nimm nun an, dass bei Pauline eine Reibungskraft von 5N und bei Paul von 10N wirkt, solange sie fahren. Wie verändert sich die Fahrt der beiden?
2) Diesmal fährt Pauline zu der Zeitmessung schon mit 1 m/s am Baum vorbei und rollt weiter. Wieder soll zunächst die Reibung vernachlässigt werden.
- a) Stelle den Kraftverlauf und die Werte von v(0), s(0) und m so ein, dass es der beschriebenen Bewegung entspricht.
- b) Wo ist Pauline nach 6 Sekunden und wie schnell ist sie?
- c) Begründe die Bewegungsgesetze durch die Betrachtung von Ableitungen (Steigungen) und Integralen (Flächen):
- [math]s(t) = v\, t = 2 \, \rm{\frac{m}{s}} \cdot t[/math]
- [math]v(t) = v_0 = 2\, \rm \frac{m}{s} [/math]
- [math]a(t) = 0 \, \rm \frac{m}{s^2}[/math]
- d) Löse b) mit Hilfe der Bewegungsgesetze.
3) Paul hat sich einen kleinen Motor an sein Board gebaut, der mit 20 Newton schiebt. Zu Beginn steht er am Baum.
- a) Stelle den Kraftverlauf und die Werte von v(0), s(0) und m so ein, dass es der beschriebenen Bewegung entspricht.
- b) Wo und wie schnell ist Paul nach 6 Sekunden?
- c) Welche Strecke legt in der Zeitspanne von 4 bis 6 Sekunden nach Beginn der Zeitmessung zurück?
- d) Begründe die Bewegungsgesetze durch die Betrachtung von Ableitungen (Steigungen) und Integralen (Flächen):
- [math]s(t) = \frac{1}{2} \, a\, t^2 = 0{,}1 \, \rm \frac{m}{s^2} \cdot t^2[/math]
- [math]v(t) = a\, t = 0{,}2 \, \rm \frac{m}{s^2} \cdot t[/math]
- [math]a(t) = \frac{F}{m} = 0{,}2 \, \rm \frac{m}{s^2}[/math]
- e) Löse b) und c) mit Hilfe der Bewegungsgesetze.
4) Pauline kommt mit 1 m/s angerauscht. Als sie am Baum vorbeifährt, sieht sie 5 Meter vor sich "Momo", die Katze der Nachbarn, sitzen. Sie bremst ab sofort mit 15 Newton.
- a) Stelle den Kraftverlauf und die Werte von v(0), s(0) und m so ein, dass es der beschriebenen Bewegung entspricht.
- b) Wie lange dauert es, bis sie steht? Schafft sie es noch vor der Katze anzuhalten? Wenn nicht, bei welcher Geschwindigkeit kollidieren die beiden?
- c) Begründe folgende Formeln für die Bremszeit und den Bremsweg:
- [math]t_{brems} = \frac{m}{F} \, v_0 [/math]
- [math]s_{brems} = \frac{1}{2}\, \frac{m}{F}\, v_0^2[/math]
- d) Wie verändert sich der Bremsweg und die Bremszeit, wenn sich die Ausgangsgeschwindigkeit verdoppelt oder halbiert?
Animation der Bewegungsdiagramme
Elisabeth fährt Skateborard.
Mit dem Schieberegler für die Zeit t oder der Schaltfläche "Los!" kann man sie fahren lassen.
Mit den orangenen Punkten im Kraft-Diagramm kann man einstellen, wie sie sich vom Boden abstößt oder bremst.
An dem grünen Punkt im Ortsdiagramm kann man Elisabeths Position zu Beginn der Zeitmessung einstellen. An dem hellblauen Punkt kann man Elisabeths Geschwindigkeit zu Beginn der Zeitmessung einstellen.
Der braune Schieberegler kann Elisabeth eine Diät verordnen oder sie wieder aufpäppeln.
Mit der Geogebra-Datei läuft die Animation flüssiger. Hier der Link zur Datei (Endung .ggb) und zum Programm.
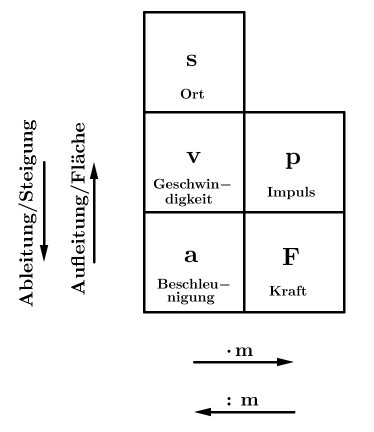
Übersichtliche Darstellung als Merkregel
|
Ort [math]s[/math] in [math]\rm m[/math] Wo ist das Ding? | |
|
Geschwindigkeit [math]v[/math] in [math]\rm \frac{m}{s}[/math] Wie schnell ist es? [math]v=\dot s \approx \frac{\triangle s}{\triangle t}[/math] [math]v=\frac{p}{m}[/math] (Entspricht dem Impuls in einem Kilogramm Masse.) |
Impuls [math]p[/math] in [math]\rm Hy[/math] Wieviel Bewegung steckt drin?
. |
|
Beschleunigung [math]a[/math] in [math]\rm \frac{m}{s^2}[/math]
[math]a=\frac{F}{m}[/math] (Entspricht der Kraft auf ein Kilogramm Masse.) |
Kraft [math]F[/math] in [math]\rm N[/math] Wie wird gedrückt/gezogen? [math]F=\dot p \approx \frac{\triangle p}{\triangle t}[/math]
. |