Elektrischer Energietransport: Beladungsmaß und Leistung: Unterschied zwischen den Versionen

Aus Schulphysikwiki
Wechseln zu: Navigation, Suche
(→‎Versuch: Kichererbsentransport)
(→‎Versuch: Eine helle Lampe)
Zeile 2: Zeile 2:
 
;Aufbau
 
;Aufbau
 
[[Datei:Stromkreis_Versuch_zwei_Lampen_Potential_als_Energiebeladungsmaß.jpg|thumb|Das linke Lampe ist an ein Netzgerät angeschlossen, die rechte über einen Schalter an die Steckdose.]]
 
[[Datei:Stromkreis_Versuch_zwei_Lampen_Potential_als_Energiebeladungsmaß.jpg|thumb|Das linke Lampe ist an ein Netzgerät angeschlossen, die rechte über einen Schalter an die Steckdose.]]
−
Eine 60W-Glühbirne ist an der Steckdose angeschlossen, die andere (4V/250mA) wird mit einer Batterie betrieben. Bei beiden Lampen wird die Stromstärke gemessen.
+
Eine 60W-Glühbirne ist an der Steckdose angeschlossen, die andere (12V/250mA) wird mit einem Netzgerät<ref>Noch schöner wäre der Vergleich zwischen Batterie und "Steckdose".</ref> betrieben. Bei beiden Lampen wird die Stromstärke gemessen.
 
;Beobachtung
 
;Beobachtung
 
Durch beide Lampen fließt der gleiche Strom mit einer Stärke von ca. 0,25 Ampère, aber die an der Steckdose angeschlossene Lampe ist viel heller!
 
Durch beide Lampen fließt der gleiche Strom mit einer Stärke von ca. 0,25 Ampère, aber die an der Steckdose angeschlossene Lampe ist viel heller!

Version vom 21. März 2016, 17:20 Uhr

Versuch: Eine helle Lampe

Aufbau
Das linke Lampe ist an ein Netzgerät angeschlossen, die rechte über einen Schalter an die Steckdose.

Eine 60W-Glühbirne ist an der Steckdose angeschlossen, die andere (12V/250mA) wird mit einem Netzgerät[1] betrieben. Bei beiden Lampen wird die Stromstärke gemessen.

Beobachtung

Durch beide Lampen fließt der gleiche Strom mit einer Stärke von ca. 0,25 Ampère, aber die an der Steckdose angeschlossene Lampe ist viel heller!

Versuch: Kichererbsentransport

Aufbau

In einer Kiste auf einer Seite des Raumes befinden sich Erbsen. (Man kann auch Streichhölzer nehmen.) Die Erbsen sollen in eine noch leere Kiste auf der anderen Seite transportiert werden. Aber jede Person darf nur zwei Erbsen nehmen!

Wir arbeiten zusammen und schauen, wie schnell wir die Erbsen transportieren können:

Energiestromstärke Leistung Versuch Erbsenstromstärke.png

In diese leere Tabelle schreiben wir unsere Ergebnisse:

Erbsen-
beladung

Zeit-
spanne

Personen-
anzahl

Erbsen-
anzahl

Personen-
stromstärke

Erbsen-
stromstärke

[math]2\,\rm \frac{E}{P}[/math]

.

.

.

.

Messwerte

Erbsen-
beladung

Zeit-
spanne

Personen-
anzahl

Erbsen-
anzahl

Personen-
stromstärke

Erbsen-
stromstärke

[math]2\,\rm \frac{E}{P}[/math]

[math]70\,\rm s[/math]

[math]69\,\rm P[/math]

[math]138\,\rm E[/math]

[math]3\,\rm \frac{E}{P}[/math]

[math]64\,\rm s[/math]

[math]64\,\rm P[/math]

[math]192\,\rm E[/math]

[math]8\,\rm \frac{E}{P}[/math]

[math]28\,\rm s[/math]

[math]21\,\rm P[/math]

[math]168\,\rm E[/math]

Auswertung

Ob wir uns bei den Erbsen verzählt haben, kann man leicht überprüfen. Die Personenanzahl multipliziert mit der Erbsenbeladung muss die Erbsenanzahl ergeben!

Die Stromstärken berechnen sich als Personen pro Zeit und als Erbsen pro Zeit:

Erbsen-
beladung

Zeit-
spanne

Personen-
anzahl

Erbsen-
anzahl

Personen-
stromstärke

Erbsen-
stromstärke

[math]2\,\rm \frac{E}{P}[/math]

[math]70\,\rm s[/math]

[math]69\,\rm P[/math]

[math]138\,\rm E[/math]

[math]\frac{69\,\rm P}{70\,\rm s}=0{,}99\,\rm \frac{P}{s}[/math]

[math]\frac{138\,\rm E}{70\,\rm s}=1{,}97\,\rm \frac{E}{s}[/math]

[math]3\,\rm \frac{E}{P}[/math]

[math]64\,\rm s[/math]

[math]64\,\rm P[/math]

[math]192\,\rm E[/math]

[math]\frac{64\,\rm P}{64\,\rm s}=1\,\rm \frac{P}{s}[/math]

[math]\frac{192\,\rm E}{64\,\rm s}=3\,\rm \frac{E}{s}[/math]

[math]8\,\rm \frac{E}{P}[/math]

[math]28\,\rm s[/math]

[math]21\,\rm P[/math]

[math]168\,\rm E[/math]

[math]\frac{21\,\rm P}{28\,\rm s}=0{,}75\,\rm \frac{P}{s}[/math]

[math]\frac{168\,\rm E}{28\,\rm s}=6\,\rm \frac{E}{s}[/math]

Man bemerkt, dass man die Erbsenstromstärke auch mit Hilfe der Personenstromstärke ausrechnen kann. Dazu muss man nur die Personenstromstärke mit der Beladung multiplizieren!

Das Potential als Energiebeladungsmaß und die elektrische Leistung

Die Batterie belädt jedes Coulomb elektrische Ladung mit 6 Joule Energie.
Es fließen 5 Coulomb pro Sekunde im Kreis.
Daher werden 30 Joule Energie pro Sekunde von der Batterie zur Lampe transportiert, die Leistung beträgt 30 Watt: [math]P=6\,\rm V \cdot 5\,\rm A = 30\,\rm W[/math].
  • Ein elektrischer Stromkreis transportiert Energie.
  • Die Stromstärke I gibt an, wieviel elektrische Ladung pro Zeit im Kreis fließt.

[math]I=\frac{Q}{t}[/math]

  • Eine Batterie belädt die elektrische Ladung mit Energie, das Potential steigt.
Bei einer Lampe wird die Energie wieder abgeladen, das Potential fällt.
  • Das Potential gibt an, mit wieviel Energie die elektrische Ladung beladen ist.

[math]\varphi=\frac{E}{Q}[/math]

  • Die Energiestromstärke oder Leistung gibt an, wieviel Energie pro Zeit transportiert wird.

[math]P=\frac{E}{t}[/math]

  • Je größer die Energiebeladung und je größer die Stromstärke, desto größer ist die Leistung.

[math]P=U\!\cdot\! I[/math]

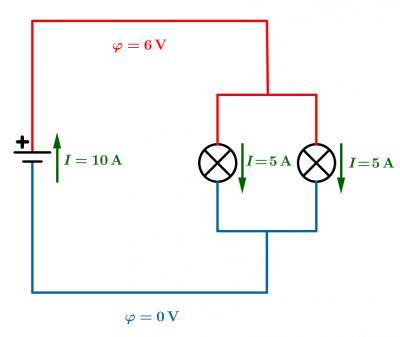
Parallelschaltung

Leistung Beispiel Parallelschaltung.png


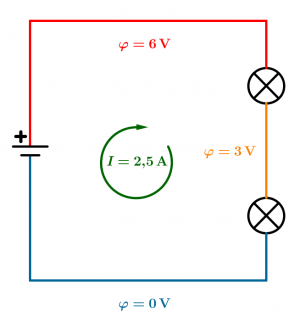
Reihenschaltung

Leistung Beispiel Reihenschaltung.png



Referenzfehler: Es sind <ref>-Tags vorhanden, jedoch wurde kein <references />-Tag gefunden.

Von „http://schulphysikwiki.de/index.php?title=Elektrischer_Energietransport:_Beladungsmaß_und_Leistung&oldid=11283“