Elektrischer Energietransport: Beladungsmaß und Leistung: Unterschied zwischen den Versionen

Aus Schulphysikwiki
Wechseln zu: Navigation, Suche
(→‎Das Potential als Energiebeladungsmaß und die elektrische Leistung)
Zeile 183: Zeile 183:
 
Man bemerkt, dass man die Erbsenstromstärke auch mit Hilfe der Personenstromstärke ausrechnen kann. Dazu muss man nur die Personenstromstärke mit der Beladung multiplizieren!
 
Man bemerkt, dass man die Erbsenstromstärke auch mit Hilfe der Personenstromstärke ausrechnen kann. Dazu muss man nur die Personenstromstärke mit der Beladung multiplizieren!
  
−
==Das Potential als Energiebeladungsmaß und die elektrische Leistung==
+
==Vergleich des Erbsentransports mit dem elektrischen Energietransport==
 
Mit Hilfe des Erbsentransportes können wir erklären, warum die Lampen so unterschiedlich hell leuchten. Dazu vergleichen wir den Erbsentransport durch Personen mit dem Energietransport durch die elektrische Ladung:
 
Mit Hilfe des Erbsentransportes können wir erklären, warum die Lampen so unterschiedlich hell leuchten. Dazu vergleichen wir den Erbsentransport durch Personen mit dem Energietransport durch die elektrische Ladung:
  
Zeile 275: Zeile 275:
 
|-
 
|-
 
|style="border-style: solid; border-width: 4px "|  
 
|style="border-style: solid; border-width: 4px "|  
−
<math>U = \frac{E}{Q}</math>
+
<math>\varphi = \frac{E}{Q}</math>
 
|style="border-style: solid; border-width: 4px "|  
 
|style="border-style: solid; border-width: 4px "|  
 
<math>t</math>
 
<math>t</math>
Zeile 287: Zeile 287:
 
<math>P = \frac{E}{t} = U\,I</math>
 
<math>P = \frac{E}{t} = U\,I</math>
 
|}
 
|}
 +
 +
==Das Potential als Energiebeladungsmaß und die elektrische Leistung==
 
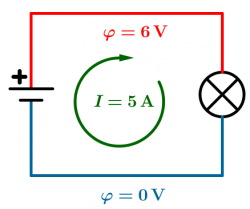
[[Datei:Leistung Beispiel.png|thumb|250px|Die Batterie belädt jedes Coulomb elektrische Ladung mit 6 Joule Energie.<br>Es fließen 5 Coulomb pro Sekunde im Kreis.<br>Daher werden 30 Joule Energie pro Sekunde von der Batterie zur Lampe transportiert, die Leistung beträgt 30 Watt: <math>P=6\,\rm V \cdot 5\,\rm A = 30\,\rm W</math>.]]
 
[[Datei:Leistung Beispiel.png|thumb|250px|Die Batterie belädt jedes Coulomb elektrische Ladung mit 6 Joule Energie.<br>Es fließen 5 Coulomb pro Sekunde im Kreis.<br>Daher werden 30 Joule Energie pro Sekunde von der Batterie zur Lampe transportiert, die Leistung beträgt 30 Watt: <math>P=6\,\rm V \cdot 5\,\rm A = 30\,\rm W</math>.]]
 
{|class="wikitable" style="border-style: solid; border-width: 4px "
 
{|class="wikitable" style="border-style: solid; border-width: 4px "

Version vom 21. März 2016, 18:19 Uhr

Versuch: Eine helle Lampe

Aufbau
Das linke Lampe ist an ein Netzgerät angeschlossen, die rechte über einen Schalter an die Steckdose.

Eine 60W-Glühbirne ist an der Steckdose angeschlossen, die andere (12V/250mA) wird mit einem Netzgerät[1] betrieben. Bei beiden Lampen wird die Stromstärke gemessen.

Beobachtung

Durch beide Lampen fließt der gleiche Strom mit einer Stärke von ca. 0,25 Ampère, aber die an der Steckdose angeschlossene Lampe ist viel heller!

Folgerung

Offensichtlich ist "der Strom aus der Steckdose" anders als "der Strom aus dem Netzgerät". Der "Steckdosenstrom" transportiert mehr Energie!

Versuch: Kichererbsentransport

Aufbau

In einer Kiste auf einer Seite des Raumes befinden sich Erbsen. (Man kann auch Streichhölzer nehmen.) Die Erbsen sollen in eine noch leere Kiste auf der anderen Seite transportiert werden. Aber jede Person darf nur zwei Erbsen nehmen!

Wir arbeiten zusammen und schauen, wie schnell wir die Erbsen transportieren können:

Energiestromstärke Leistung Versuch Erbsenstromstärke.png

In diese leere Tabelle schreiben wir unsere Ergebnisse:

Erbsen-
beladung

Zeit-
spanne

Personen-
anzahl

Erbsen-
anzahl

Personen-
stromstärke

Erbsen-
stromstärke

[math]2\,\rm \frac{E}{P}[/math]

.

.

.

.

Messwerte

Erbsen-
beladung

Zeit-
spanne

Personen-
anzahl

Erbsen-
anzahl

Personen-
stromstärke

Erbsen-
stromstärke

[math]2\,\rm \frac{E}{P}[/math]

[math]70\,\rm s[/math]

[math]69\,\rm P[/math]

[math]138\,\rm E[/math]

[math]3\,\rm \frac{E}{P}[/math]

[math]64\,\rm s[/math]

[math]64\,\rm P[/math]

[math]192\,\rm E[/math]

[math]8\,\rm \frac{E}{P}[/math]

[math]28\,\rm s[/math]

[math]21\,\rm P[/math]

[math]168\,\rm E[/math]

Auswertung

Ob wir uns bei den Erbsen verzählt haben, kann man leicht überprüfen. Die Personenanzahl multipliziert mit der Erbsenbeladung muss die Erbsenanzahl ergeben!

Die Stromstärken berechnen sich als Personen pro Zeit und als Erbsen pro Zeit:

Erbsen-
beladung

Zeit-
spanne

Personen-
anzahl

Erbsen-
anzahl

Personen-
stromstärke

Erbsen-
stromstärke

[math]2\,\rm \frac{E}{P}[/math]

[math]70\,\rm s[/math]

[math]69\,\rm P[/math]

[math]138\,\rm E[/math]

[math]\frac{69\,\rm P}{70\,\rm s}=0{,}99\,\rm \frac{P}{s}[/math]

[math]\frac{138\,\rm E}{70\,\rm s}=1{,}97\,\rm \frac{E}{s}[/math]

[math]3\,\rm \frac{E}{P}[/math]

[math]64\,\rm s[/math]

[math]64\,\rm P[/math]

[math]192\,\rm E[/math]

[math]\frac{64\,\rm P}{64\,\rm s}=1\,\rm \frac{P}{s}[/math]

[math]\frac{192\,\rm E}{64\,\rm s}=3\,\rm \frac{E}{s}[/math]

[math]8\,\rm \frac{E}{P}[/math]

[math]28\,\rm s[/math]

[math]21\,\rm P[/math]

[math]168\,\rm E[/math]

[math]\frac{21\,\rm P}{28\,\rm s}=0{,}75\,\rm \frac{P}{s}[/math]

[math]\frac{168\,\rm E}{28\,\rm s}=6\,\rm \frac{E}{s}[/math]

Man bemerkt, dass man die Erbsenstromstärke auch mit Hilfe der Personenstromstärke ausrechnen kann. Dazu muss man nur die Personenstromstärke mit der Beladung multiplizieren!

Vergleich des Erbsentransports mit dem elektrischen Energietransport

Mit Hilfe des Erbsentransportes können wir erklären, warum die Lampen so unterschiedlich hell leuchten. Dazu vergleichen wir den Erbsentransport durch Personen mit dem Energietransport durch die elektrische Ladung:

  • Die im Kreis laufenden Personen entsprechen der im Kreis fließenden Ladung: [math] \text{1 Person } \widehat{=} \text{ 1 Coulomb}[/math]
  • Die transportierten Erbsen entsprechen der transportierten Energie: [math] \text{1 Erbse } \widehat{=} \text{ 1 Joule}[/math]
  • Die Erbsenbeladung entspricht dem elektrischen Potential: [math] \text{1 Erbse pro Person } \widehat{=} \text{ 1 Joule pro Coulomb}[/math]

Jetzt können wir die entsprechende Tabelle aufstellen:

Energie-
beladung

Zeit-
spanne

Ladungs-
menge

Energie-
menge

(Ladungs-)
Stromstärke

Energie-
stromstärke
(Leistung)

[math]12\,\rm V = 12\,\rm \frac{J}{C}[/math]

[math]0{,}25\,\rm A=0{,}25\,\rm \frac{C}{s}[/math]

[math]230\,\rm V = 230\,\rm \frac{J}{C}[/math]

[math]0{,}25\,\rm A=0{,}25\,\rm \frac{C}{s}[/math]

Weil wir die Zeitdauer nicht kennen, die Lampen können ja eine Sekunde oder eine Stunde lang angeschaltet sein, können wir uns eine wählen.

Wählt man als Zeitdauer eine Sekunde, ist es einfach die geflossene Ladungsmenge zu bestimmen, denn bei einer Stromstärke von 0,25 Ampère fließen ja gerade 0,25 Coulomb pro Sekunde! In zwei Sekunden fließen daher 0,5 Coulomb usw.

Die transportierte Energiemenge ergibt sich aus der geflossenen Ladung mal dem Beladungsmaß.

Die Energiestromstärke kann man jetzt entweder als Energie pro Zeit berechnen oder als Ladungsstromstärke mal Beladungsmaß.

Energie-
beladung

Zeit-
spanne

Ladungs-
menge

Energie-
menge

(Ladungs-)
Stromstärke

Energie-
stromstärke
(Leistung)

[math]12\,\rm V = 12\,\rm \frac{J}{C}[/math]

[math]1\,\rm s[/math]

[math]0{,}25\,\rm C[/math]

[math]3\,\rm J[/math]

[math]0{,}25\,\rm A=0{,}25\,\rm \frac{C}{s}[/math]

[math]3\,\rm \frac{J}{s}[/math]

[math]230\,\rm V = 12\,\rm \frac{J}{C}[/math]

[math]60\,\rm s[/math]

[math]15\,\rm C[/math]

[math]3450\,\rm J[/math]

[math]0{,}25\,\rm A=0{,}25\,\rm \frac{C}{s}[/math]

[math]57{,}5\,\rm \frac{J}{s}[/math]

[math]\varphi = \frac{E}{Q}[/math]

[math]t[/math]

[math]Q[/math]

[math]E[/math]

[math]I = \frac{Q}{t}[/math]

[math]P = \frac{E}{t} = U\,I[/math]

Das Potential als Energiebeladungsmaß und die elektrische Leistung

Die Batterie belädt jedes Coulomb elektrische Ladung mit 6 Joule Energie.
Es fließen 5 Coulomb pro Sekunde im Kreis.
Daher werden 30 Joule Energie pro Sekunde von der Batterie zur Lampe transportiert, die Leistung beträgt 30 Watt: [math]P=6\,\rm V \cdot 5\,\rm A = 30\,\rm W[/math].
  • Ein elektrischer Stromkreis transportiert Energie.
  • Die Stromstärke I gibt an, wieviel elektrische Ladung pro Zeit im Kreis fließt.

[math]I=\frac{Q}{t}[/math]

  • Eine Batterie belädt die elektrische Ladung mit Energie, das Potential steigt.
Bei einer Lampe wird die Energie wieder abgeladen, das Potential fällt.
  • Das Potential gibt an, mit wieviel Energie die elektrische Ladung beladen ist.

[math]\varphi=\frac{E}{Q}[/math]

  • Die Energiestromstärke oder Leistung gibt an, wieviel Energie pro Zeit transportiert wird.

[math]P=\frac{E}{t}[/math]

  • Je größer die Energiebeladung und je größer die Stromstärke, desto größer ist die Leistung.

[math]P=U\!\cdot\! I[/math]

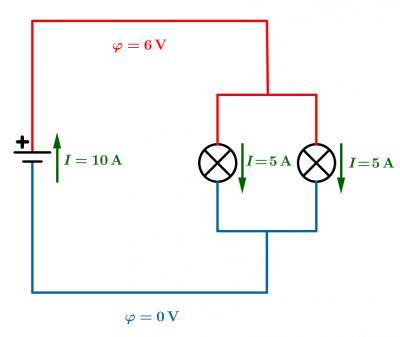
Parallelschaltung

Leistung Beispiel Parallelschaltung.png


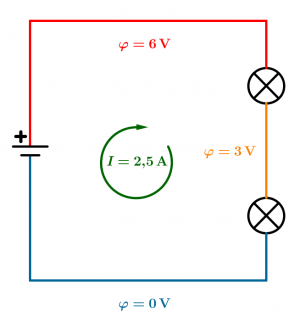
Reihenschaltung

Leistung Beispiel Reihenschaltung.png


Fußnoten

  1. ↑ Noch schöner wäre der Vergleich zwischen Batterie und "Steckdose".
Von „http://schulphysikwiki.de/index.php?title=Elektrischer_Energietransport:_Beladungsmaß_und_Leistung&oldid=11289“