Aufgaben zum Licht als Welle (Lösungen): Unterschied zwischen den Versionen
(→5) Doppelspalt quantitativ) |
(→7) Einzelspalt) |
||
| Zeile 270: | Zeile 270: | ||
Beleuchtet man einen schmalen Spalt mit weißem Licht, so kann man dahinter ein buntes Streifenmuster auf einem Schirm beobachten. | Beleuchtet man einen schmalen Spalt mit weißem Licht, so kann man dahinter ein buntes Streifenmuster auf einem Schirm beobachten. | ||
*Wie kommt es zu den wiederholten dunklen Stellen? Fertigen Sie eine Zeichnung zur Begründung an. | *Wie kommt es zu den wiederholten dunklen Stellen? Fertigen Sie eine Zeichnung zur Begründung an. | ||
| + | [[Datei:Wellenwanne Spalt groß f20Hz.jpg|thumb|Ein Einzelspaltmuster mit [[Beugung an Öffnungen und Hindernissen#Versuche in der Wellenwanne|Wasserwellen.]] ]] | ||
| + | ::Man kann die dunklen Stellen mit dem [[Das Huygenssche Prinzip|Huygensschen Prinzip]] erklären: | ||
| + | ::Jede Stelle im Spalt ist Ausgangspunkt einer Elementarwelle, welche sich hinter dem Spalt überlagern. | ||
| + | ::Zu den dunklen Stellen am Schirm (Minima) haben die Randstrahlen einen Gangunterschied, der ein Vielfaches der Wellenlänge beträgt. (vgl. [http://www.roro-seiten.de/physik/lk12/optik/einfachspalt__gangunterschied.html dieses Bild]) | ||
| + | ::Man kann dann alle Elementarwellen in eine gerade Anzahl von Teilbündel einteilen, die sich paarweise auslöschen, weil sie einen Gangunterschied von einer halben Wellenlänge haben. | ||
*Wie kommt es zu den farbigen Rändern der hellen Stellen? | *Wie kommt es zu den farbigen Rändern der hellen Stellen? | ||
:Sind die hellen Stellen nach Außen hin oder zur Mitte hin rot? Begründen Sie. | :Sind die hellen Stellen nach Außen hin oder zur Mitte hin rot? Begründen Sie. | ||
Version vom 24. November 2017, 11:26 Uhr
(Kursstufe > Die Welleneigenschaften des Lichts)
Inhaltsverzeichnis
- 1 1) Interferenz im Alltag
- 2 2) Typische Welleneigenschaften
- 3 3) Beispiel-Experiment
- 4 4) Doppelspalt qualitativ
- 5 5) Doppelspalt quantitativ
- 6 6) Lichtfarben und Wellenlänge
- 7 7) Einzelspalt
- 8 8) Haaresbreite
- 9 9) Ein Seidenschal
- 10 10) Eine CD oder DVD
- 11 11) Mehrfachspalt und Zeigeraddition
- 12 Fußnoten
1) Interferenz im Alltag
Die Interferenz, also die Überlagerung, von Licht tritt grundsätzlich immer auf. So kann Licht aus zwei Lampen zum Beispiel quer durch das Zimmer "fliegen" und sich durchkreuzen. Lichtschwerter wie in Star Wars gibt es nicht:).
Nur das typische Muster, die periodische Schwankung der Intensität, ist nicht immer zu beobachten. Solche Muster treten bei Wellen dann auf, wenn der Abstand der Lichtquellen oder die Breite eines Hindernisses im Bereich von einigen Wellenlänge des Lichtes liegt. (Vgl. Beugung an Öffnungen und Hindernissen) Im Alltag ist die Wellenlänge des Lichtes aber viel kleiner als die Breite der meisten Gegenstände. Ein Haar ist aber so klein, dass man Interferenzphänomene beobachten kann, oder auch das enge Gewebe eines Vorhangs.
CDs haben so feine Muster, dass sie in bunten Farben schillern und auch Vögel nutzen Interferenz um ein leuchtend buntes Federkleid zu haben.
- Hält man ein Haar direkt vor das Auge und schaut in eine eng begrenzte, helle Lichtquelle, wie z.B. eine weit entfernte helle Lampe, dann sieht man nebenstehendes Bild.
- a) Zeichnen Sie ein, in welcher Richtung das Haar verläuft.
- b) Erklären Sie die regelmäßigen farbigen Stellen innerhalb des Lichtstreifens.
- Das Licht der Lampe wird am Haar in den Schattenraum gebeugt. Die Beugung geschieht nur senkrecht zum Haar, deshalb sieht man den Lichtstreifen senkrecht zur Haarrichtung.
- Hinter dem Haar überlagern sich die Lichtwellen die von beiden Seiten des Haares kommen und es gibt ein Interferenzmuster, ähnlich wie bei den zwei Lautsprechern.
- Das Licht der Lampe besteht aber aus elektromagnetischen Wellen verschiedener Wellenlänge, was wir als verschiedene Farben wahrnehmen. Rotes Licht mit großer Wellenlänge erzeugt auch ein großes Interferenzmuster, das heißt die Maxima liegen weiter auseinander. Das gelbe Muster ist kleiner und das blaue am kleinsten. Was man sieht ist die Überlagerung aller dieser Muster. (Diese Animation von Claus Wolfseher, Katharinen-Gymnasium Ingolstadt gibt einen Eindruck davon.)
2) Typische Welleneigenschaften
Typische Welleneigenschaften, die man auch von mechanischen Wellen kennt, sind:
Isaac Newton hat Licht als einen Strom von Teilchen beschrieben und konnte damit einfach die Reflektion wie das Abspringen von Bällen an einer Wand erklären. Auch die Brechung konnte er mit einer größeren Ausbreitungsgeschwindigkeit in einem Medium erklären. Die Beugung, also die Ablenkung, von Teilchen in der Nähe eines Hindernisses zu erklären hat auch Newton größere Probleme bereitet.
Vollkommen unvereinbar mit der Vorstellung von Lichtteilchen sind aber Interferenzerscheinungen. Vor allem das Zustandekommen eines Minimums ist nicht zu erklären. Denn wie sollen sich an einem Ort auftreffende Lichtteilchen gegenseitig auslöschen?
3) Beispiel-Experiment
Gegenstände oder speziell aufgebaute Experimente, bei denen man Interferenzmuster beobachten kann, sind ein guter Nachweis für den Wellencharakter von Licht:
Im Alltag: Schillernde CDs, Hologramme von Geldscheinen, [Seifenblasen, schillernde Federn von Vögeln, Perlmutt, ... (Siehe auch hier)
Im Experiment: Doppelspalt, Einzelspalt, Gitter, ...
4) Doppelspalt qualitativ
Der Doppelspaltversuch ist auch mit mechanischen Wellen durchführbar und hier erklärt.
Der Versuch mit Licht ist hier beschrieben.
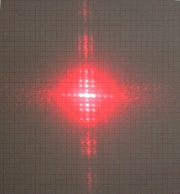
5) Doppelspalt quantitativ
Ein Doppelspalt wird vom Licht einer Glühlampe beleuchtet. Die Spaltmitten haben einen Abstand von 0,1mm und der Schirm steht 90cm hinter dem Spalt. Das Foto zeigt das Interferenzmuster auf dem Schirm. Zur Entfernungsmessung dient ein Geodreieck mit einer cm-Skala
- Berechnen Sie aus dem Abstand des zweiten oder dritten Maximums vom nullten Maximum die Wellenlängen von rotem und blauem Licht und vergleichen Sie das Ergebnis mit Literaturwerten.
- Die Abstände zwischen dem 2. und 0. Maximum sind ungefähr:
- [math]a_{blau}=8\,\rm mm \qquad a_{rot} = 12\,\rm mm[/math]
- Beim 2. Maximum beträgt der Gangunterschied der Mittelpunktstrahlen gerade zwei Wellenlängen. Die Interferenzbedingung muß man dann nur noch nach der Wellenlänge auflösen:
- [math]\sin (\alpha) = \frac{\Delta s}{d} = \frac{2 \lambda}{d}\approx \frac{a}{l} [/math]
- [math]\lambda = \frac{1}{2} d \frac{a}{l}[/math]
- [math]\lambda_{blau} = \frac{1}{2} 0{,}1\,\rm mm \cdot \frac{8\,\rm mm}{90\,\rm cm} =\frac{1}{2} \cdot 0{,}1\,\rm mm \cdot \frac{8\,\rm mm}{900\,\rm mm} = 0{,}444\cdot 10^{-3}\,\rm mm = 444\,\rm nm[/math]
- [math]\lambda_{rot} = \frac{1}{2} \cdot 0{,}1\,\rm mm \cdot \frac{12\,\rm mm}{90\,\rm cm} =\frac{1}{2} \cdot 0{,}1\,\rm mm \cdot \frac{12\,\rm mm}{900\,\rm mm} = 0{,}666\cdot 10^{-3}\,\rm mm = 666\,\rm nm[/math]
Die gemessenen Werte stimmen in etwa mit den Angaben auf Wikipedia überein.
6) Lichtfarben und Wellenlänge
Ein Gitter wird vom Licht einer Glühlampe beleuchtet. Hinter dem Gitter ist im Abstand von 60cm ein Schirm. (Versuchsaufbau) Hier die Ergebnisse:
a) Bestimmen Sie aus den Messergebnissen die Wellenlänge von violettem, blauen, grünem, gelben und rotem Licht. Vergleichen Sie Ihre Ergebnisse mit Literaturwerten.
Zur Berechnung der Wellenlängen kann man die gleiche Formel wie beim Doppelspalt heranziehen. Der Abstand der Spaltmitten d beim Doppelspalt entspricht hier ebenfalls dem Abstand der Spaltmitten, der sogenannten Gitterkonstante.
- Gitter mit 80 Linien pro mm
- [math]\frac{\Delta s}{d} \approx \frac{a}{l}[/math]
Der Gangunterschied beträgt beim 1. Maximum gerade eine Wellenlänge, beim zweiten Maximum zwei Wellenlängen. Um die Wellenlänge zu berechnen muss man also nach dem Gangunterschied auflösen:
- [math]\Delta s = \frac{a}{l}\, d[/math]
|
[math] \begin{array}{rrcl} \textsf{1.Max:}& \Delta s &=& \lambda \\ \Rightarrow & \lambda &=& \frac{a_1}{l}\,d \\ & &=& \frac{a_1}{0{,6}\,\rm m}\cdot \frac{1}{80}\cdot 10^{-3}\,\rm m \\ & &=& \,a_1\cdot2{,}083\cdot 10^{-5}\,\rm m \\ \end{array} [/math] |
[math] \begin{array}{rrcl} \textsf{2.Max:}& \Delta s &=& 2 \, \lambda \\ \Rightarrow & \lambda &=& \frac{1}{2}\,\frac{a_2}{l}\,d \\ & &=& \frac{1}{2}\, \frac{a_2}{0{,6}\,\rm m}\cdot \frac{1}{80}\cdot 10^{-3}\,\rm m \\ & &=& \,a_2\cdot 1{,}042\cdot 10^{-5}\,\rm m \\ \end{array} [/math] |
|
violett |
blau |
grün |
gelb |
rot | |
|
[math]\textsf{1.Max:}\ a_1\ \text{(in cm)}[/math] |
[math]2{,}0[/math] |
[math]2{,}2[/math] |
[math]2{,}6[/math] |
[math]2{,}8[/math] |
[math]3{,}2[/math] |
|
[math]\textsf{2.Max:}\ a_2\ \text{(in cm)}[/math] |
[math]4{,}0[/math] |
[math]4{,}5[/math] |
[math]5{,}2[/math] |
[math]5{,}6[/math] |
[math]6{,}1[/math] |
|
[math]\textsf{1.Max:}\ \lambda\ \text{(in nm)}[/math] |
417 |
458 |
542 |
583 |
667 |
|
[math]\textsf{2.Max:}\ \lambda\ \text{(in nm)}[/math] |
417 |
469 |
542 |
583 |
635 |
Obwohl man die Abweichungen vom 0. Maximum auf den Bildern nicht so genau abmessen kann, stimmen die gemessenen Werte stimmen sehr gut mit den Literaturwerten überein.
- Gitter mit 300 Linien pro mm
Das Maximum erster Ordnung ist so breit, dass man für die einzelnen Farben ganze Wellenlängenbereiche angeben kann.
[math] \begin{array}{rrcl} & \Delta s &=& \lambda \\ \Rightarrow & \lambda &=& \frac{a_1}{l}\,d \\ & &=& \frac{a_1}{0{,6}\,\rm m}\cdot \frac{1}{300}\cdot 10^{-3}\,\rm m \\ & &=& \,a_1\cdot5{,}556\cdot 10^{-6}\,\rm m \\ \end{array} [/math]
|
violett ab |
blau ab |
grün ab |
gelb |
rot ab |
rot bis | |
|
[math] a_1\ \text{(in cm)}[/math] |
[math]7{,}5[/math] |
[math]8{,}5[/math] |
[math]9{,}2[/math] |
[math]10{,}6[/math] |
[math]11{,}0[/math] |
[math]12{,}5[/math] |
|
[math]\lambda\ \text{(in nm)}[/math] |
417 |
472 |
511 |
589 |
611 |
667 |
Vergleich man mit den Literaturwerten, so stellt man Abweichungen fest, die nicht nur an der Genauigkeit des Ablesens liegen können. Insbesondere stimmen die kürzeste und die längste Wellenlänge nicht mit den Literaturwerten überein. Zu Berücksichtigen ist, dass die Digitalkamera die gemessenen Farbwerte in nur drei Grundarben (rot, grün, blau) abspeichert und so den Originalfarbton nur nachahmen kann[1] Das Ablesen am Experiment bringt bestimmt deutlich bessere Werte.
b) Warum ist das Maximum nullter Ordnung weiss und nicht bunt wie die anderen?
Je größer die Wellenlänge, desto größer ist auch das Interferenzmuster. Deshalb liegen die roten Maxima weiter außen als die blauen. Nur beim nullten Maxima gibt es keine Unterschiede zwischen den Wellenlängen, denn dort beträgt der Gangunterschied für alle Farben Null. Deshalb überlagern sich dort alle Farben und das Maxima ist weiß.
c) Zu dem Gitter mit 80 Linien pro mm:
- Warum ist das zweite Maximum breiter als das erste?
- Begründen Sie, dass das zweite Maximum doppelt so breit sein müsste wie das erste. Wie breit ist demnach das dritte?
Der Gangunterschied für das erste Maximum beträgt eine Wellenlänge, für das zweite Maximum zwei Wellenlängen. Bei violettem Licht, mit seiner kleinen Wellenlänge [math]\lambda_v[/math], reicht daher schon eine geringe Abweichung vom nullten Maximum, für rotes Licht muss die Abweichung größer sein:
|
1. Max: |
violett: |
[math] \frac{\lambda_v}{d} = \frac{a_v}{l} \qquad \Rightarrow \quad a_v = \frac{l}{d}\, \lambda_v [/math] |
||
|
rot: |
[math] \frac{\lambda_r}{d} = \frac{a_r}{l} \qquad \Rightarrow \quad a_r = \frac{l}{d}\, \lambda_r \qquad \Rightarrow \quad a_r-a_v=\frac{l}{d}(\lambda_r-\lambda_v)[/math] |
|||
|
2. Max: |
violett: |
[math] \frac{2\,\lambda_v}{d} = \frac{a_v}{l} \qquad \Rightarrow \quad a_v = 2\,\frac{l}{d}\, \lambda_v [/math] |
||
|
rot: |
[math] \frac{2\,\lambda_r}{d} = \frac{a_r}{l} \qquad \Rightarrow \quad a_r = 2\,\frac{l}{d}\, \lambda_r \qquad \Rightarrow \quad a_r-a_v=2\,\frac{l}{d}(\lambda_r-\lambda_v)[/math] |
Das zweite Maximum ist daher doppelt so breit wie das erste. Die Breite des n-ten Maximums beträgt näherungsweise für "kleine" Winkel:
- [math] a_r-a_v= n\,\frac{l}{d}(\lambda_r-\lambda_v)[/math]
7) Einzelspalt
Beleuchtet man einen schmalen Spalt mit weißem Licht, so kann man dahinter ein buntes Streifenmuster auf einem Schirm beobachten.
- Wie kommt es zu den wiederholten dunklen Stellen? Fertigen Sie eine Zeichnung zur Begründung an.

- Man kann die dunklen Stellen mit dem Huygensschen Prinzip erklären:
- Jede Stelle im Spalt ist Ausgangspunkt einer Elementarwelle, welche sich hinter dem Spalt überlagern.
- Zu den dunklen Stellen am Schirm (Minima) haben die Randstrahlen einen Gangunterschied, der ein Vielfaches der Wellenlänge beträgt. (vgl. dieses Bild)
- Man kann dann alle Elementarwellen in eine gerade Anzahl von Teilbündel einteilen, die sich paarweise auslöschen, weil sie einen Gangunterschied von einer halben Wellenlänge haben.
- Wie kommt es zu den farbigen Rändern der hellen Stellen?
- Sind die hellen Stellen nach Außen hin oder zur Mitte hin rot? Begründen Sie.
Ein Einzelspalt hat eine Breite von genau einer Wellenlänge des einfallenden Lichtes.
- Unter welchem Winkel ist das Maximum nullter Ordnung zu sehen?
8) Haaresbreite
a) Bestimmen Sie mit aus den Messergebnissen des "Haarschattenversuchs" die Wellenlänge des Laserlichts.
Näherungsweise kann man den Versuch als Doppelspaltexperiment auffassen, bei dem vom rechten und linken Rand des Haars jeweils eine Lichtwelle ausgeht.
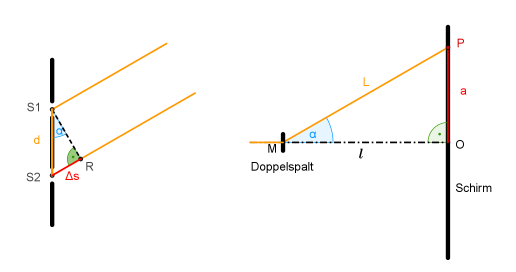
Die Spaltmitten haben einen Abstand [math]d[/math] voneinander und [math]\Delta s[/math] ist der Gangunterschied der beiden Strahlen.
- [math]\sin(\alpha) = \frac{\triangle s}{d} = \frac{a}{L} =\frac{a}{\sqrt{a^2+l^2}}\approx \frac{a}{l} \qquad \triangle s: \text{Gangunterschied zu den ''Spaltmitten''}[/math]
- [math]\triangle s = k \ \lambda \qquad \qquad \text{konstruktive Interferenz: Maximum k-ter Ordnung (k= 0,1,...)}[/math]
- [math]\triangle s = k \ \lambda - 1/2 \ \lambda \quad \text{destruktive Interferenz: Minimum k-ter Ordnung (k= 1,2,...)}[/math]
Wir messen folgende Größen mit Mikrometerschraube und Lineal bei dem roten Laser:
Dicke des Haares: 0,05 mm Abstand Haar-Wand: 1 m Abstand Mitte des Musters - 2. dunkle Stelle: 1,8 cm
Man hat an der Stelle des 2. Minimums gemessen, der Gangunterschied beträgt daher [math]\Delta s = \frac{3}{2} \lambda[/math]:
- [math]\frac{\frac{3}{2} \lambda}{d} \approx \frac{a}{l}[/math]
Das kann man nun nach der Wellenlänge auflösen:
- [math]\lambda= \frac{2}{3} \frac{a}{l}\, d =\frac{2}{3} \frac{1{,}8\,\rm cm}{100\,\rm cm}\cdot 0{,}05\cdot 10^{-3}\,\rm m = 6\cdot 10^{-7}\,\rm m = 600\,\rm nm[/math]
Das ist nicht sonderlich genau, ergibt aber einen ungefähren Wert.
b) Mit einem Laserpointer läßt man rotes Licht der Wellenlänge 650nm auf ein Haar fallen. Die Dicke des Haares hat man vorher zu 5 Hundertstel mm gemessen. Auf der 2m entfernten Wand kann man nun eine interessante Beobachtung machen.
Zeichnen Sie das auf der Wand sichtbare Muster in Originalgröße.
9) Ein Seidenschal
- Ein roter Laserpointer, mit einer Wellenlänge von 630nm wird auf einen Schal gerichtet. Drei Meter hinter dem Schal kann man folgende Beobachtung machen:
- Erklären Sie die Beobachtung. Welche Eigenschaften des Schals können Sie daraus berechnen?
- Oder genauer: Bestimmen Sie die Dicke der Fäden und die Breite der Lücken in horizontaler und vertikaler Richtung.
10) Eine CD oder DVD
Ein Laserpointer wird auf eine CD gerichtet. Man macht folgende Beobachtung:
Zwischen den Maxima Nullter und erster Ordnung bildet sich ein Winkel von 22°.
a) Die CD mit ihren eng beieinanderliegenden Rillen stellt ein Reflektionsgitter dar. Der Abstand der Rillen entspricht der Gitterkonstante [math]d[/math]. Der Zusammenhang zwischen Winkel, Gangunterschied und Gitterkonstante beträgt:
- [math]\sin(\alpha) = \frac{\Delta s}{d}[/math]
Die Gleichung kann man nach der Gitterkonstanten auflösen:
- [math]d = \frac{\Delta s}{\sin(\alpha)}[/math]
Der Gangunterschied ist beim 1. Maximum gerade eine Wellenlänge:
- [math]d = \frac{\lambda}{\sin(\alpha)}= \frac{630\cdot 10^{-9}\,\rm m}{\sin(22^\circ)} = 1{,}68\cdot 10^{-6}\,\rm m = [/math]
Der Rillenabstand beträgt ungefähr [math]1{,}5[/math] Tausendstel Millimeter. Das Messergebnis stimmt gut mit dem genormten Spurabstand einer CD überein. Auf einen Millimeter gibt es also eine Menge Rillen:
- [math] 1\,\rm mm \,\colon 0{,}00168\,\rm mm = 595[/math]
Eine CD hat ca. 600 Rillen pro Millimeter! Und bei einer beschreibbaren Breite von ca. 30mm folgt daraus, dass die Schreibspur ca. 18000 mal um das innere Loch "gewickelt" ist.
b) Um den Winkel zum Maximum zweiter Ordnung zu bestimmen, setzt man den Gangunterschied gleich zwei Wellenlängen:
- [math]\sin(\alpha_2) = \frac{\Delta s}{d} = \frac{2\, \lambda}{d} = 2\, \frac{\lambda}{d} [/math]
Der Sinus des Winkels des 2. Maximums hat also den doppelten Wert im Vergleich zum 1. Maximum:
- [math]\sin(\alpha_2) = 2\, \sin(22^\circ) [/math]
Für kleine Winkel ergibt sich daraus eine Verdoppelung des Winkels, also 44°. Diese Kleinwinkelnäherung ist aber bei 22° schon recht ungenau. Mit Hilfe der inversen Sinusfunktion kann man exakt nach dem Winkel auflösen:
- [math]\alpha_2 = \sin^{-1}\left( 2\, \sin(22^\circ) \right) = 58{,}5^\circ [/math]
Der Winkel, unter dem das Maximum zweiter Ordnung erscheint, beträgt schon fast 60°.
c) Eine DVD hat einen geringen Spurabstand von lediglich [math]0{,}74\,\rm \mu m = 740\,\rm nm[/math], wodurch auch eine größere Datenkapazität erreicht wird. Der Spurabstand ist so klein, dass er bereits der Wellenlänge von rotem Licht entspricht! Auf einen Millimeter kommen ca. 1350 Spuren.
Wegen der kleineren Gitterkonstante werden die Winkel der Maxima auch größer, denn der zu erreichende Gangunterschied bleibt ja gleich. Beim ersten Maximum beträgt der Gangunterschied eine Wellenlänge, also 630nm:
- [math]\sin(\alpha_{\rm DVD}) = \frac{\lambda}{d_{\rm DVD}}[/math]
- [math]\alpha_{\rm DVD} = \sin^{-1}\left(\frac{630\,\rm nm}{0{,}74\,\rm \mu m}\right) = 58,4^\circ[/math]
Der Winkel des ersten Maximums ist bereits so groß wie der des zweiten Maximums bei der CD. Das liegt daran, dass der Spurabstand ungefähr halbiert wurde.
Für ein zweites Maximum müsste der Gangunterschied 1260nm betragen. Weil aber die Gitterkonstante nur 740nm beträgt, kann dieser Gangunterschied nicht erreicht werden! Die DVD erzeugt daher nur das Maximum erster Ordnung.
11) Mehrfachspalt und Zeigeraddition
Das nebenstehende Bild zeigt das Bild eines Schirms hinter einem beleuchteten Mehrfachspalt. Der verwendete Laser hat eine Wellenlänge von 532nm und der Abstand zwischen Spalt und Schirm beträgt 1m.
- Wieviele Spalte hat der Mehrfachspalt? Begründen Sie in Worten und mit Hilfe von Zeigeraddition.
- Wie breit sind die einzelnen Spalte und wie groß ist der Mittenabstand zwischen den Spalten?
Fußnoten
- ↑ Siehe auch die Seiten: Digitaler Sensor-Die Fotoschule, Alles über Kamera-Sensoren, Aufbau einer DSLR-Kamera.