Der Photoeffekt: Unterschied zwischen den Versionen

Aus Schulphysikwiki
Wechseln zu: Navigation, Suche
(→‎Versuch: Photonenmessung mit einem Zählrohr)
Zeile 111: Zeile 111:
 
*Video: [https://www.experimente.physik.uni-freiburg.de/H_Atom_und_Kernphysik/photoeffekt/nachweisphotonenzaehlrohr Nachweis von Photonen mittels Zählrohr] der Uni Freiburg
 
*Video: [https://www.experimente.physik.uni-freiburg.de/H_Atom_und_Kernphysik/photoeffekt/nachweisphotonenzaehlrohr Nachweis von Photonen mittels Zählrohr] der Uni Freiburg
 
;Beobachtung
 
;Beobachtung
−
Der an das Zählrohr angeschlossene Lautsprecher sendet Knack-Geräusche aus. Je näher die Kerze am Zählrohr steht, desto öfter knackt es. Die Glasscheibe verhindert das Knacken.
+
Der an das Zählrohr angeschlossene Lautsprecher sendet in unregelmäßigem zeitlichen Abstand Knack-Geräusche aus. Je näher die Kerze am Zählrohr steht, desto öfter knackt es. Die Glasscheibe verhindert das Knacken.
−
;Folgerung
+
;Erklärung
 +
Das Zählrohr reagiert auf ionisierende Strahlung, in diesem Fall die von der Kerze ausgesendete UV-Strahlung. Die Glasscheibe läßt nur das sichtbare Licht hindurch, dass zur Ionisierung nicht ausreicht.
  
 
==Fußnoten==
 
==Fußnoten==

Version vom 6. Februar 2023, 18:41 Uhr

(Kursstufe > Licht als Teilchen)

Beispiele

  • Röntgenstrahlen, UV-Licht, Radiowellen, alles elektromagnetische Wellen...

  • Aber einen solchen Sonnenbrand bekommt man nicht im Auto, oder?

  • Die Milch ist in einer "Lichtschutzflasche" abgefüllt.

  • Wie groß ist die Strahlenbelastung bei Flügen...

  • oder Röntgenaufnahmen!?

  • Gamma-Strahlen können sogar tödlich sein!

  • Handystrahlung ist bestimmt nicht tödlich, aber umstritten.

  • Wenn die Batterien schlapp machen...

Zitate

"Unter Lichtstrahlen verstehe ich die kleinsten Theilchen des Lichts, und zwar sowohl nach einander in denselben Linien, als gleichzeitig in verschiedenen. Denn es ist klar, dass das Licht sowohl aus succesiven, wie aus gleichzeitigen Theilchen besteht, da man an der nämlichen Stelle das in einem bestimmten Augenblicke ankommende Licht auffangen und gleichzeitig das nachkommende vorbeilassen kann, und ebenso kann man im nämlichen Augenblicke das Licht an einer Stelle auffangen und an einer anderen vorbeilassen. Denn das aufgefangene Licht kann nicht dasselbe sein, wie das vorbeigelassene. Das kleinste Licht oder Lichttheilchen, welches getrennt von dem übrigen Lichte für sich allein aufgefangen werden kann, oder allein etwas thut oder erleidet, was das übrige Licht nicht thut, noch erleidet, - dies nenne ich einen Lichtstrahl." (Isaac Newton, 1704)[1]
  • "Anders als z. B. Röntgenstrahlung kann UV-Strahlung den menschlichen Körper nicht durchdringen, sondern wird in den obersten Hautschichten absorbiert, wo die Strahlungsenergie in photochemische Reaktionsenergie umgewandelt wird. Ultraviolette Strahlung kann also beim Menschen Schäden an der Haut und an den Augen verursachen. Die Absorption erfolgt in sogenannten Chromophoren – DNS (DNA), RNS (RNA), Proteinen, Pigmenten (z. B. Melanin)."[2]
  • "Biochemische Wirkungen [...] sind immer dann zu erwarten, wenn die Energieübertragung zu Ionisationen [...] führt. Der Energiebedarf für eine Ionisation beträgt etwa 15 eV [...]. Tatsächlich wird in [...] typischen menschlichen Geweben im Mittel ein Energiebetrag von 30 eV zur Erzeugung eines Ionenpaares benötigt. Die Hälfte der Energie wird also offensichtlich ohne Ionisation übertragen."[3]

Ionisierende Strahlung

Ionisationsenergien verschiedenener Atome

Elektromagnetische Wellen können gefährlich sein. Liegt ein Mensch zu lange in der Sonne, kann er Sonnenbrand bekommen. Dabei werden durch die UV-Strahlung Hautzellen abgetötet. Die rote Färbung der Haut kommt durch die starke Durchblutung zustande, wenn der Körper die Haut wieder "repariert". Bei Flügen in großen Höhen ist man der Röntgen- und Gammastrahlung aus dem Weltraum stärker ausgesetzt als auf der Erde, weil die schützende Luftschicht dünner ist. Dadurch steigt das Krebsrisiko leicht an, denn die Strahlung kann zu Veränderungen im Erbgut führen.

UV-Strahlen können aber auch Wasser desinfizieren, in dem sie Bakterien abtöten. Dazu müssen mit dem Wasser gefüllte Kunststofflaschen einige Stunden in die direkte Sonne gelegt werden.

Elektromagnetische Wellen mit kleiner Wellenlänge können also Atome ionisieren oder sogar chemische Bindungen trennen. Langwellige Strahlen können das nicht.

Versuch: Der Photoeffekt qualitativ

Die Hg-hochdrucklampe ist über eine Drossel an eine Spannungsquelle mit 230V angeschlossen.
Aufbau
Eine Zinkplatte wird mit Schmirgelpapier blank gerieben und auf ein Elektroskop gesteckt. Das Zink wird mit Hilfe eines geriebenen Kunststoffstabes negativ geladen oder mit einem geriebenem Glasstab positiv geladen.
Dann wird die Zinkplatte mit einer Glühlampe oder mit einer Quecksilberhochdrucklampe angeleuchtet.
Zwischen die Lampe und der Zinkplatte kann man noch eine Glasplatte halten.
Beobachtung
Das Licht der Hg-Lampe ist wesentlich weniger intensiv als das der helleren Glühbirne und bläulich.
Wird die negativ geladene Zinkplatte von der Hg-Lampe beleuchtet, so zeigt das Elektroskop eine Entladung an. In allen anderen Fällen, also mit der Glühlampe oder bei positiv geladenem Zink passiert nichts, der Zeiger des Elektroskops bewegt sich nicht. Auch die Glasplatte zwischen Hg-Lampe und negativ geladenem Zink verhindert die Entladung, obwohl das bläuliche Licht weiterhin auf die Zinkplatte fällt.
Folgerung
Das Elektroskop wird negativ geladen, indem zusätzliche Elektronen auf das Zink gebracht werden. Eine Entladung der negativen Zinkplatte bedeutet, dass die überschüssigen Elektronen vom Zink entfernt werden. Das Licht der Glühlampe ist dazu offensichtlich nicht in der Lage, das Licht der Hg-Lampe aber sehr wohl.
Die Glasplatte läßt sichtbares Licht durch, verhindert aber die Entladung, woraus man schließen kann, dass die Hg-Lampe offensichtlich auch elektromagnetische Wellen aussendet, die im nicht sichtbaren Breich liegen. Dieser Anteil muss die Entladung auslösen. Langwellige infrarot-Strahlung kann es nicht sein, denn die wird von der Glühbirne auch ausgesendet. Außerdem deutet die bläuliche Farbe des Hg-Lampen-Lichtes an, dass sie wohl auch kurzwelliges ultraviolettes Licht aussendet.[4]
Kurzwelliges UV-Licht kann also Elektronen aus Zink lösen, das langwelligere sichtbare Licht aber nicht!
Zum Auslösen der Elektronen aus der Zinkplatte wird Energie benötigt, denn die Elektronen sind an die Atomrümpfe gebunden. Diese Energie wird von der elektromagnetischen Welle geliefert. Aber warum kann dann das langwellige Licht keine Elektronen auslösen? Auch sichtbares Licht kann beliebig viel Energie transportieren, das ist nur eine Frage der Intensität, also der Amplitude der elektrischen und magnetischen Felder. Offensichtlich kann die Wellentheorie dies nicht erklären!
Um eine Erklärung zu liefern, muss man die Sichtweise auf Licht ändern. Auch wenn die Interferenz von Licht für das Wellenmodell spricht und auch die Maxwellgleichungen stark für die Existenz von elektromagnetischen Wellen sprechen, kann man versuchen den Photoeffekt mit Hilfe einer Teilchentheorie zu erklären. Licht besteht dann aus einem Strom von vielen, kleinen Teilchen. Die unterschiedlichen Farben des Lichtes kommen durch unterschiedliche Lichtteilchen zustande. Treffen diese Teilchen auf das negativ geladene Zink, so schlagen sie Elektronen heraus. Die Teilchen des sichtbaren Lichtes sind dazu aber nicht in der Lage. Daraus kann man schließen, dass immer nur ein Lichtteilchen ein Elektron herauslöst. Die Lichtteilchen sind wohl wenig kooperativ. Die Teilchen des sichtbaren Lichtes tragen zu wenig Energie, um ein Elektron auszulösen, die Energie der Teilchen des UV-Lichtes aber reicht aus. Offenbar nimmt die Energiemenge eines Lichtteilchens mit der Wellenlänge ab!
Wir haben nun die unangenehme Situation, dass es verschiedene Experimente gibt, die wir nicht mit einer Theorie erklären können. Die destruktive Interferenz beim Doppelspalt ist im Rahmen der Teilchentheorie unverständlich, ebenso wie der Photoeffekt für die Wellentheorie. Was nun?

Versuch: Der Photoeffekt quantitativ

Bevor man die Frage nach dem richtigen Modell für das Licht klärt kann man das Teilchenmodell noch ausbauen. Wir untersuchen wieviel Energie denn ein Lichtteilchen transportiert und wie die Energiemenge von der Wellenlänge abhängt. Schon in diesem Satz wird der Widerspruch deutlich: Man spricht von einer Wellenlänge und einem Teilchen, als ob ein Teilchen eine Wellenlänge hätte.

Aufbau
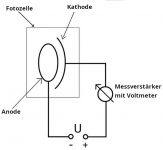
Es gibt verschiedene Möglichkeiten den Photoeffekt genauer zu untersuchen. Hier wird eine Photozelle[5] verwendet, die durch Bestrahlung mit Licht eine elektrische Spannung erzeugt, welche gemessen wird.

  • Die Spannung der Fotozelle wird mit einem Messverstärker gemessen, weil nur ganz geringe Ströme fließen.

  • Eine Fotozelle. Im Hintergrund des Glasbehälters die Kathode, aus der Elektronen gelöst werden. Der Draht im Vordergrund ist die Anode.

  • Fotozelle Zeichnung.png

  • Quecksilberdampflampe im Betrieb mit ihrem charakteristischen Spektrum

Um verschiedene Wellenlängen zu untersuchen werden Farbfilter verwendet, die nur eine bestimmte Wellenlänge hindurchlassen. Die Farbfilter sind nicht in der Lage eine exakte Wellenlänge herauszufiltern. Aber das Licht der Quecksilberdampflampe hat ein Linienspektrum, aus dem die Filter die besonders hellen Linien herausfiltern.
Messung
Bei Bestrahlung durch das Licht stellt sich schnell eine konstante Spannung ein. Für die verschiedenen Wellenlängen wurde gemessen: 
Farbe   | Wellenlänge | Spannung
gelb    |   578nm     | 0,6V
grün    |   546nm     | 0,65V
violett |   436nm     | 1,1V
Auswertung
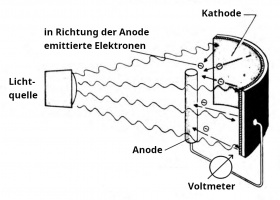
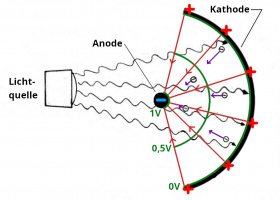
Trifft das Licht auf das Kathodenmaterial[6], so löst es Elektronen aus, die auch die Anode treffen.[7] Dadurch lädt sich die Kathode positiv und die Anode negativ auf und es bildet sich ein elektrisches Feld. Das Feld ist so gerichtet, dass es die ausgelösten Elektronen von der negativ geladenen Anode wegdrückt. Die Ladungsverschiebung hält also nur so lange an, bis die kinetische Energie der ausgelösten Elektronen nicht mehr ausreicht, um zur Anode zu gelangen. Dann ist die maximale elektrische Feldstärke erreicht und auch die maximale Spannung. Diese Spannung haben wir gemessen. Die Spannung ist also ein Maß für die kinetische Energie der Elektronen. Offensichtlich haben die von den violetten Lichtteilchen ausgelösten Elektronen die größte Bewegungsenergie.

  • Die vom Licht ausgelösten Elektronen treffen unter anderem auch auf die Anode. Die Kathode wird positiv, die Anode negativ geladen.

  • Durch das elektrische Feld werden die Elektronen gebremst und erreichen die Anode gerade nicht mehr.

Zur Berechnung der kinetischen Energie verwendet man die gemessene Spannung. Um einen Potentialunterschied von U zu überwinden, benötigt ein Elektron mit der Ladung [math]Q=e[/math] die Energiemenge[8]:
[math]E_{kin}=E_{el}=Q\, U=e\,U[/math]
Es ist praktisch als Energieeinheit ein "Elektronenvolt" zu verwenden. Das ist die Energiemenge, die ein Elektron bei einem Potentialunterschied von einem Volt benötigt oder bekommt:
[math]1\rm\, eV=1\rm\,e \cdot 1\rm\, V = 1{,}6\cdot 10^{-19}\rm\, C \cdot 1\rm\, V = 1{,}6\cdot 10^{-19}\rm\, C \cdot \frac{1\rm\, J}{1\rm\, C} =1{,}6\cdot 10^{-19}\rm\, J[/math]
Die gemessenen Bewegungsenergien werden nun in Abhängigkeit von der Lichtfrequenz aufgetragen: (Hier kann man seine EIGENEN MESSWERTE EINTRAGEN!))

(Zur Datei und zum Programm)

Die kinetische Energie der Elektronen steigt linear mit der Frequenz der Lichtteilchen. (Das sieht man vor allem bei Messungen mit vielen Wellenlängen.) Deshalb ist es sinnvoll eine Ausgleichsgerade durch die Messpunkte zu legen.
Die Energie der Elektronen ist geringer als die Energie der Photonen, weil auch für das Auslösen des Elektrons aus der Kathode Energie benötigt wird. Die Bewegungsenergie hängt also linear mit der Frequenz zusammen:
[math]E_{kin}(f)=E_{ph}(f)-W_A \quad[/math], was der Geradengleichung [math]g(x)=m\,x-b[/math] entspricht.
Die Energie der Lichtteilchen erhält man, indem man zur kinetischen Energie der Elektronen noch die zum Auslösen benötigte Energie addiert.
An den Geraden lassen sich wichtige Informationen ablesen:
1) Die Photonenenergie steigt proportional zur Frequenz.
2) Die Austrittsenergie (oder Austrittsarbeit), die benötigt wird, um ein Elektron aus dieser Kathode auszulösen, beträgt ca. 1eV.
3) Ab einer Frequenz von ca. [math]3{,}3\cdot10^{14}\rm\, Hz[/math] ist ein Lichtteilchen in der Lage ein Elektron auszulösen. Das ist die Grenzfrequenz.
Aus der Steigung der Gerade läßt sich der Proportionalitätsfaktor zwischen Photonenenergie und Frequenz berechnen:
[math]\frac{\Delta E}{\Delta f}=\frac{2\rm\, eV}{6{,}6\cdot 10^{14}\rm\, Hz}=30{,}30\cdot 10^{-16}\rm\, \tfrac{\rm eV}{\rm Hz}[/math]
Es ist aber üblich die Photonenenergie in Joule anzugeben und nicht in eV:
[math]30{,}30\cdot 10^{-16}\rm\, \tfrac{\rm eV}{\rm Hz} = 30{,}30\cdot 10^{-16} \cdot 1{,}6\cdot10^{-19} \tfrac{\rm J}{\rm Hz} = 4{,}9\cdot 10^{-34}\tfrac{\rm J}{\rm Hz}[/math]
Das ist das berühmte Plancksche Wirkumsquantum h! Es gibt an, wie die Photonenenergie mit der Frequenz zunimmt. Unser Messwert ist um ca. 27% zu klein, was für eine Messung mit nur drei Messwerten in Ordnung ist.

Die Energie eines Lichtteilchens (Photon) ist proportional zu seiner Frequenz:

[math]E=h\, f[/math]

mit [math]h=6{,}66\cdot 10^{-34}\tfrac{\rm J}{\rm Hz}[/math] "Planksches Wirkungsquantum"

Damit berechnet sich die kinetische Energie des ausgelösten Elektrons zu:
[math] e\, U = h\,f -W_A[/math]

Versuch: Photonenmessung mit einem Zählrohr

Aufbau

Eine Kerze wird vor ein Geiger-Müller-Zählrohr gestellt. Der Abstand wird variiert und eine Glasscheibe zwischen Kerze und Zählrohr gestellt.

Beobachtung

Der an das Zählrohr angeschlossene Lautsprecher sendet in unregelmäßigem zeitlichen Abstand Knack-Geräusche aus. Je näher die Kerze am Zählrohr steht, desto öfter knackt es. Die Glasscheibe verhindert das Knacken.

Erklärung

Das Zählrohr reagiert auf ionisierende Strahlung, in diesem Fall die von der Kerze ausgesendete UV-Strahlung. Die Glasscheibe läßt nur das sichtbare Licht hindurch, dass zur Ionisierung nicht ausreicht.

Fußnoten

  1. ↑ Newton, Isaac: "Optik; oder, Abhandlung über Spiegelungen, Brechungen, Beugungen und Farben des Lichts", Robert Oppenheim, Berlin, 1898 (Original von 1704) (Online bei Internet Archive), S.5
  2. ↑ Fachverband für Strahlenschutz e. V.: "Leitfaden „Ultraviolettstrahlung künstlicher Quellen“, S.6
  3. ↑ Hanno Krieger: "Grundlagen der Strahlungsphysik und des Strahlungsschutzes", Vieweg, 2012, S. 391
  4. ↑ Deshalb ist es auch wichtig im Umgang mit der Hg-Lampe vorsichtig zu sein und möglichst nicht in die Lampe zu schauen oder eine Schutzbrille aus Glas zu tragen. Das nicht sichtbare UV-Licht kann die Netzhaut angreifen ohne dass das Auge durch einen Schließreflex sich schützt.
  5. ↑ Von Phywe (06779-00).
  6. ↑ Das Kathodenmaterial besteht hier nicht aus Zink, das von sichtbarem Licht nicht ionisiert werden kann.
  7. ↑ Die meißten Elektronen treffen die Anode nicht, aber das spielt keine Rolle.
  8. ↑ Der Potentialunterschied, also die Spannung, des elektrischen Feldes entspricht im Gravitationsfeld dem Höhenunterschied. Siehe auch "das Potential".

Literatur/Links

Biologische Wirkung

Bindungsenergien

Transparenz von Glas und Kunststoffen

Von „http://schulphysikwiki.de/index.php?title=Der_Photoeffekt&oldid=16904“