Aufgaben zur Energieübertragung mit einer Kraft (Lösungen): Unterschied zwischen den Versionen

Version vom 16. Mai 2011, 21:16 Uhr

[math]p= F \, t = 40 N \cdot 5 sec = 200 N sec = 200 Hy[/math]

[math]E= F\, s = 40 N \cdot 7,5 m = 300 N m = 300 J[/math]

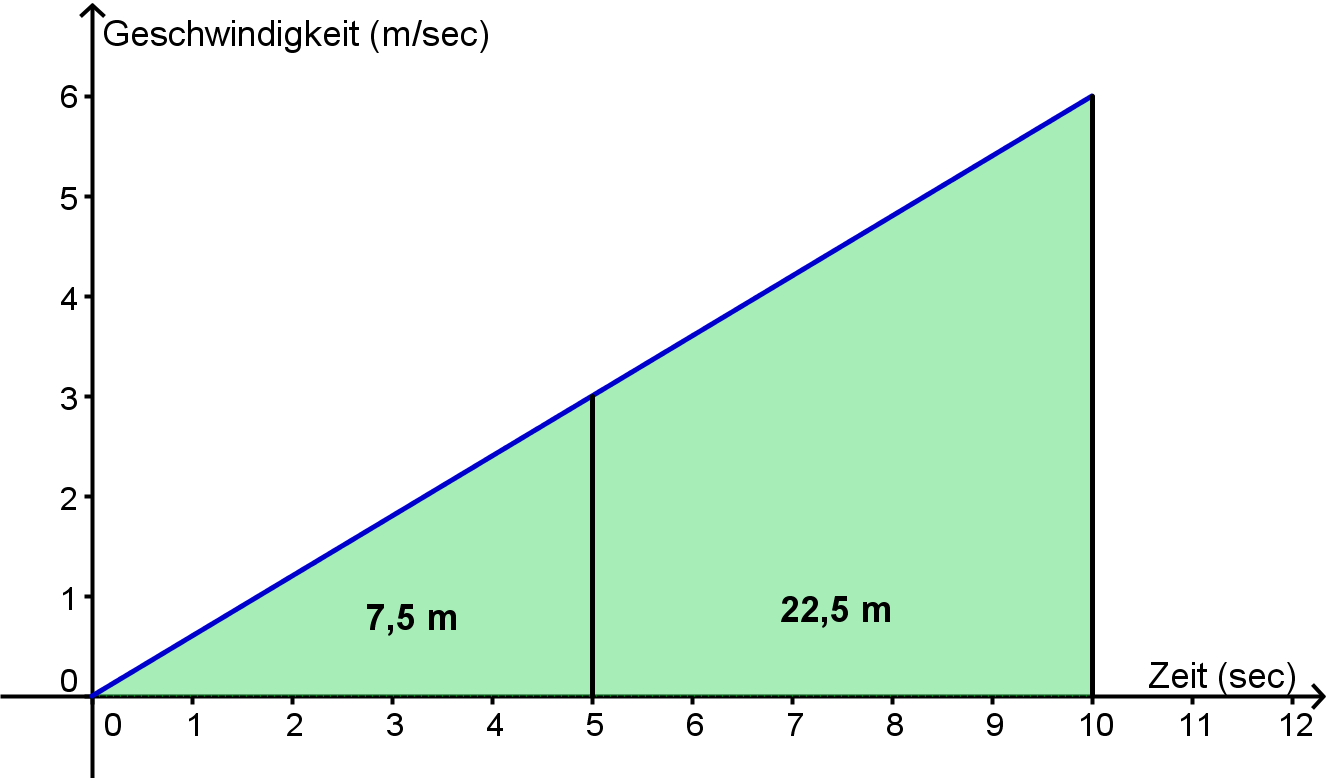
Das Rad ist ja nach 5 Sekunden nicht mehr in Ruhe. Durch die immer größere Geschwindigkeit legt es auch in gleichen Zeiten größere Strecken zurück. Genau sieht man das im v-t-Diagramm. Wegen der konstanten Kraft nimmt die Geschwindigkeit wie der Impuls linear zu, die Fläche unter dem dem Graphen entspricht dem zurückgelegten Weg:

Man sieht, dass das Rad in den zweiten 5 Sekunden den dreifachen Weg zurücklegt!

[math]\triangle p= F \, t = 40 N \cdot 5 sec = 200 N sec = 200 Hy[/math]

[math]\triangle E= F\, s = 40 N \cdot 22,5 m = 900 N m = 900 J[/math]

Insgesamt stecken also [math]400 Hy [/math] Impuls und [math]1200 J[/math] Energie im Rad!

(Für Neugierige und Schlaue: Im v-t-Diagramm kann man ablesen, dass die FahrerIn nach 5 Sekunden 3 m/sec schnell sein muss. Da der Impuls 200 Hy beträgt hat sie also eine Masse von 76 kg.)

Die Kraft auf die Pedale ist achtmal so groß wie die Kraft zwischen Rad und Straße, also beträgt sie 320 Newton.

Um die Kraft konstant zu halten, müßte die RadlerIn in Bewegungsrichtung der Pedale immer mit 320 N Ziehen bzw. Drücken. Realistisch ist aber, dass sie besonders stark Runterdrücken kann und damit die Kraft besonders bei waagrecht stehenden Pedalen groß ist.

@@ Zeile 12: / Zeile 12: @@
 :<math>\triangle E= F\, s = 40 N \cdot 22,5 m = 900 N m = 900 J</math>
 Insgesamt stecken also <math>400 Hy </math> Impuls und <math>1200 J</math> Energie im Rad!
 *(Für Neugierige und Schlaue: Im v-t-Diagramm kann man ablesen, dass die FahrerIn nach 5 Sekunden 3 m/sec schnell sein muss. Da der Impuls 200 Hy beträgt hat sie also eine Masse von 76 kg.)
-Das Zahnrad an der Kurbel ("Kettenblatt") hat 52 Zähne, das hintere ("Ritzel") nur 13. Der Radius des Rades beträgt ungefähr das Doppelte der Kurbellänge. Damit ist die Übersetzung der Gangschaaltung 1:4, insgesamt beträgt die Übersetzung von der Kurbel auf das Rad 1:8. Dreht man also die Kurbel um einen Zentimeter, so bewegt sich der äußere Rand des Rades und somit das Fahrrad um 8 Zentimeter.
 *Die Kraft auf die Pedale ist achtmal so groß wie die Kraft zwischen Rad und Straße, also beträgt sie 320 Newton.
 *Um die Kraft konstant zu halten, müßte die RadlerIn in Bewegungsrichtung der Pedale immer mit 320 N Ziehen bzw. Drücken. Realistisch ist aber, dass sie besonders stark Runterdrücken kann und damit die Kraft besonders bei waagrecht stehenden Pedalen groß ist.