Aufgaben zur Energieübertragung mit einer Kraft (Lösungen): Unterschied zwischen den Versionen
Aus Schulphysikwiki
(→Nach Oben) |
(→Laufen) |
||
| Zeile 45: | Zeile 45: | ||
===Laufen=== | ===Laufen=== | ||
| − | + | [[Datei:Laufen_Kreidelinie.jpg|thumb|Die beim Laufen an die Tafel gemalte Linie.]] | |
| − | | | + | Die Schrittlänge betrug ca. 60 cm mit einem Höhenunterschied von ca. 4 cm. |
| − | + | ||
| − | + | Bei einer Masse von 80 kg benötigt man <math>800 N \cdot 0,04 m = 32 J</math> für einen Schritt. Dabei setzt man voraus, dass man die Energie zum Hochheben nicht mehr zurückerhält. Sie wird wohl zur Erwärmung von Schuhen, Gelnken, Muskeln, etc. verwendet. | |
| − | + | ||
| − | + | Mit 2000000 Joule kann man demnach 62500 Schritte machen, also 37,5 km weit laufen! | |
| − | + | ||
| − | + | ||
Version vom 18. Mai 2011, 12:53 Uhr
Inhaltsverzeichnis
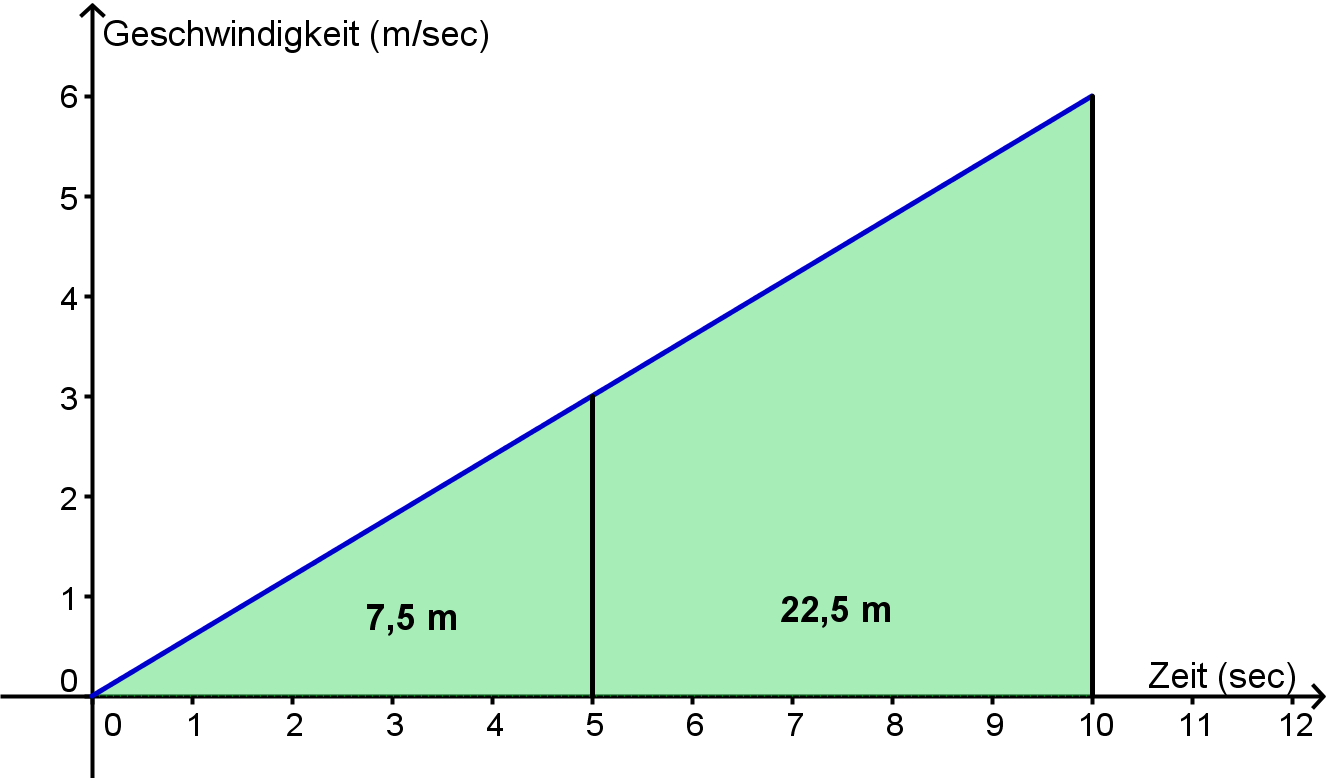
Ein Fahrrad beschleunigt
- Es gilt:
- [math]p= F \, t = 40 N \cdot 5 sec = 200 N sec = 200 Hy[/math]
- [math]E= F\, s = 40 N \cdot 7,5 m = 300 N m = 300 J[/math]
- Das Rad ist ja nach 5 Sekunden nicht mehr in Ruhe. Durch die immer größere Geschwindigkeit legt es auch in gleichen Zeiten größere Strecken zurück. Genau sieht man das im v-t-Diagramm. Wegen der konstanten Kraft nimmt die Geschwindigkeit wie der Impuls linear zu, die Fläche unter dem dem Graphen entspricht dem zurückgelegten Weg:
- Es gilt:
- [math]\triangle p= F \, t = 40 N \cdot 5 sec = 200 N sec = 200 Hy[/math]
- [math]\triangle E= F\, s = 40 N \cdot 22,5 m = 900 N m = 900 J[/math]
Insgesamt stecken also [math]400 Hy [/math] Impuls und [math]1200 J[/math] Energie im Rad!
- (Für Neugierige und Schlaue: Im v-t-Diagramm kann man ablesen, dass die FahrerIn nach 5 Sekunden 3 m/sec schnell sein muss. Da der Impuls 200 Hy beträgt hat sie also eine Masse von 76 kg.)
- Die Kraft auf die Pedale ist achtmal so groß wie die Kraft zwischen Rad und Straße, also beträgt sie 320 Newton.
- Um die Kraft konstant zu halten, müßte die RadlerIn in Bewegungsrichtung der Pedale immer mit 320 N Ziehen bzw. Drücken. Realistisch ist aber, dass sie besonders stark Runterdrücken kann und damit die Kraft besonders bei waagrecht stehenden Pedalen groß ist.
Zange
- Am Griff ist der Weg, den die Hand beim Drücken zurücklegt länger als der den die Schneide zurücklegt. Die Wege sind Kreisbögen und weil der Umfang proportional zum Radius ist, ist der Weg der Hand [math]9 / 1,5 = 6[/math] mal so lang.
- Also ist die Kraft an der Schneide 6 mal größer und beträgt 450 Newton.
- Je näher der Draht dem Drehpunkt ist und je weiter Außen man den Griff drückt, umso größer ist die Hebelwirkung.
Nach Oben
Um auf den Schauinsland zu kommen, muss man ca. 1000 Höhenmeter überwinden. Wieviel Energie ist wohl dazu nötig?
- Beim Hochheben eines 5kg-Gewichtes muss man eine Kraft von ca. 50 Newton aufwenden. Diese Kraft wirkt längs einer Strecke der Länge von zwei Metern. Die übertragene Energiemenge ist also:
- [math]E=F\, s = 50 N \cdot 2 m = 100 Nm = 100 J[/math].
- Entscheidend für die Energieübertragung ist die in Richtung der Bewegung wirkende Kraft, also die Kraft parallel zum Boden. Je steiler der Weg, desto größer wird diese Kraft. Im Gegenzug wird aber auch der Weg kürzer! Das kann man auch mathematisch untersuchen:
- An den ähnlichen Dreiecken kann man die Verhältnisse ablesen:
- [math]\frac{F_p}{G}=\frac{H \ddot o he}{Weg}=\sin \alpha[/math]
- Woraus folgt:
- [math]F_p \cdot Weg = G \cdot H\ddot o he = ben \ddot o tigte Energiemenge[/math]
- Bei einer Masse von 80 kg benötigt man [math]G \cdot H\ddot o he = 800 N \cdot 1000m = 800000 J = 800 kJ[/math].
- (Wenn man die Energie einer Tafel Schoki von ca. 2000 kJ zu 1/3 "verwertet", so reicht eine Tafel gerade so aus.)
Laufen
Die Schrittlänge betrug ca. 60 cm mit einem Höhenunterschied von ca. 4 cm.
Bei einer Masse von 80 kg benötigt man [math]800 N \cdot 0,04 m = 32 J[/math] für einen Schritt. Dabei setzt man voraus, dass man die Energie zum Hochheben nicht mehr zurückerhält. Sie wird wohl zur Erwärmung von Schuhen, Gelnken, Muskeln, etc. verwendet.
Mit 2000000 Joule kann man demnach 62500 Schritte machen, also 37,5 km weit laufen!