Aufgaben zum Konzept der Energie: Unterschied zwischen den Versionen
Aus Schulphysikwiki
K (→Lageenergie eines Wasserturms) |
|||
| Zeile 22: | Zeile 22: | ||
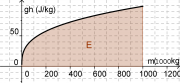
Man füllt den Turm mit einem konstanten Wasserstrom auf. Das Diagramm zeigt den Zusammenhang zwischen Wassermasse und Füllhöhe mal Ortsfaktor. Bestimmen Sie die Energiemenge durch eine ungefähre Flächenbestimmung. Jedes Rechteck entspricht <math>100kg \cdot 10\frac{J}{kg}=1000J</math>. | Man füllt den Turm mit einem konstanten Wasserstrom auf. Das Diagramm zeigt den Zusammenhang zwischen Wassermasse und Füllhöhe mal Ortsfaktor. Bestimmen Sie die Energiemenge durch eine ungefähre Flächenbestimmung. Jedes Rechteck entspricht <math>100kg \cdot 10\frac{J}{kg}=1000J</math>. | ||
| + | <br style="clear: both" /> | ||
Version vom 26. Oktober 2011, 16:18 Uhr
Energiebedarf eines Menschen
Ein Mensch benötigt täglich etwa 10000 kJ Energie, die er durch das Essen erhält. (genauere Werte findet man zB. bei Wikipedia.)
- Berechnen Sie die mittlere Leistung in Watt.
Nudeln haben einen Brennwert von 1400 kJ/kg.
- Welche Menge an Nudeln müßte man pro Tag und wieviel pro Sekunde essen, wenn man damit ausschließlich seinen Energiebedarf deckt?
- Vergleichen Sie die Berechnung der "Nudelstromstärke" mit der Berechnung der elektrischen Leistung [math]P = U \cdot I[/math].
Lageenergie eines Wasserturms
- Wieviel Lageenergie steckt wohl in dem Wasser des Turms? Genauer: Wieviel Energie könnte man erhalten, wenn man das Wasser am Fuße des Turmes herauslaufen läßt?
Der Wasserturm ist in etwa 20m breit und die maximale Wasserhöhe beträgt etwa 10m. Die tragende Betonsäule ist ca. 45m lang.
Erste Abschäzung
Schätzen Sie die mittlere Höhe des Wassers und berechnen so einen ersten Näherungswert.
Integrieren
Man füllt den Turm mit einem konstanten Wasserstrom auf. Das Diagramm zeigt den Zusammenhang zwischen Wassermasse und Füllhöhe mal Ortsfaktor. Bestimmen Sie die Energiemenge durch eine ungefähre Flächenbestimmung. Jedes Rechteck entspricht [math]100kg \cdot 10\frac{J}{kg}=1000J[/math].