Praktikum: Untersuchung von Schwingungen mit der Differentialgleichung: Unterschied zwischen den Versionen
Aus Schulphysikwiki
K (hat „Praktikum: Bestimmung von Differentialgleichungen“ nach „Praktikum: Untersuchung von Schwingungen mit der Differentialgleichung“ verschoben: Besserer Titel) |
K |
||
| Zeile 5: | Zeile 5: | ||
* Überlegen Sie sich zuerst, wovon die Frequenz der Schwingung abhängen könnte. Schreiben Sie auf, welche Veränderung Sie erwarten und warum: Z.B. "Bei größerer Masse wird die Frequenz kleiner, wegen der größeren Trägheit." | * Überlegen Sie sich zuerst, wovon die Frequenz der Schwingung abhängen könnte. Schreiben Sie auf, welche Veränderung Sie erwarten und warum: Z.B. "Bei größerer Masse wird die Frequenz kleiner, wegen der größeren Trägheit." | ||
| + | :Überlegen Sie sich ausserdem, ob die Schwingung harmonisch ist, oder nicht. | ||
* Danach ist es sinnvoll die Differentialgleichung aufzustellen. | * Danach ist es sinnvoll die Differentialgleichung aufzustellen. | ||
:Zunächst muss man ein Koordinatensystem wählen, also eine Methode angeben mit der man die Position des Gegenstands beschreiben kann. Danach muss man den Zusammenhang zwischen Auslenkung und Rückstellkraft <math>F(y)</math> bestimmen. Die DGL ergbt sich dann immer als <math>m\, \ddot y = F(y)</math>. | :Zunächst muss man ein Koordinatensystem wählen, also eine Methode angeben mit der man die Position des Gegenstands beschreiben kann. Danach muss man den Zusammenhang zwischen Auslenkung und Rückstellkraft <math>F(y)</math> bestimmen. Die DGL ergbt sich dann immer als <math>m\, \ddot y = F(y)</math>. | ||
:Vor allem beim Fadenpendel hilft auch ein Blick in ein Buch oder ins Internet weiter. | :Vor allem beim Fadenpendel hilft auch ein Blick in ein Buch oder ins Internet weiter. | ||
| + | :Jetzt können Sie auch beurteilen, ob die Schwingung wirklich harmonisch ist! | ||
* Danach sollen sie Lösungen <math>y(t)</math> der DGL und eine Formel für die Frequenz <math>f</math> oder die Kreisfrequenz <math>\omega</math> angeben. | * Danach sollen sie Lösungen <math>y(t)</math> der DGL und eine Formel für die Frequenz <math>f</math> oder die Kreisfrequenz <math>\omega</math> angeben. | ||
| Zeile 16: | Zeile 18: | ||
:Mit dieser harmonischen Näherung können Sie weiterrechnen :) | :Mit dieser harmonischen Näherung können Sie weiterrechnen :) | ||
| − | * Welche Schlussfolgerung können Sie aus der allgemeinen Lösung ziehen? Genauer: Wovon hängt die Frequenz der Schwingung ab? (Z.B. | + | * Welche Schlussfolgerung können Sie aus der allgemeinen Lösung ziehen? Genauer: Wovon hängt die Frequenz der Schwingung ab? (Z.B. proportional zur Masse und zur Amplitude, etc.) |
* Ausserdem können Sie nun ihre Rechnungen durch eine Messung überprüfen. Messen Sie die zur Berechnung der Frequenz nötigen Werte, führen sie eine [[Messunsicherheit_und_Fehlerrechnung|Fehlerrechnung]] durch und vergleichen Sie die gemessene mit der berechneten Frequenz. | * Ausserdem können Sie nun ihre Rechnungen durch eine Messung überprüfen. Messen Sie die zur Berechnung der Frequenz nötigen Werte, führen sie eine [[Messunsicherheit_und_Fehlerrechnung|Fehlerrechnung]] durch und vergleichen Sie die gemessene mit der berechneten Frequenz. | ||
Version vom 9. Januar 2012, 10:27 Uhr
- Ziel der Untersuchung ist es, das -Zeit-Orts-Gesetz [math] y(t)[/math] und damit auch die Frequenz der Schwingung aus der äußeren Situation, wie z.B. die Masse eines Körpers herzuleiten.
- Überlegen Sie sich zuerst, wovon die Frequenz der Schwingung abhängen könnte. Schreiben Sie auf, welche Veränderung Sie erwarten und warum: Z.B. "Bei größerer Masse wird die Frequenz kleiner, wegen der größeren Trägheit."
- Überlegen Sie sich ausserdem, ob die Schwingung harmonisch ist, oder nicht.
- Danach ist es sinnvoll die Differentialgleichung aufzustellen.
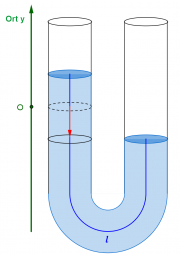
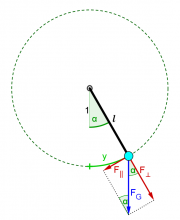
- Zunächst muss man ein Koordinatensystem wählen, also eine Methode angeben mit der man die Position des Gegenstands beschreiben kann. Danach muss man den Zusammenhang zwischen Auslenkung und Rückstellkraft [math]F(y)[/math] bestimmen. Die DGL ergbt sich dann immer als [math]m\, \ddot y = F(y)[/math].
- Vor allem beim Fadenpendel hilft auch ein Blick in ein Buch oder ins Internet weiter.
- Jetzt können Sie auch beurteilen, ob die Schwingung wirklich harmonisch ist!
- Danach sollen sie Lösungen [math]y(t)[/math] der DGL und eine Formel für die Frequenz [math]f[/math] oder die Kreisfrequenz [math]\omega[/math] angeben.
- Im Fall einer harmonischen Schwingung kann man die Lösungen wie im Fall des schwingenden Wagens finden. Die DGL hat dann die Form [math]\ddot y = - k \, y[/math] mit einer positiven Konstante [math]k[/math].
- Bei einer nichtharmonischen Schwingung mit nichtlinearem Kraftverlauf hat man leider verloren, denn solche DGL sind schwer oder garnicht lösbar. Es gibt aber einen Ausweg: Man nimmt den linearen Kraftverlauf, der die Situation am besten annähert:
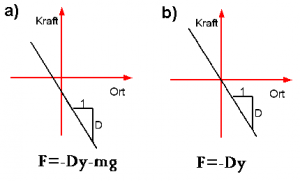
- Zeichnen Sie den Graphen von [math]F(y)[/math]. Zeichnen Sie die Tangente in [math]y=0[/math] ein und bestimmen Sie die Tangentengleichung. Die Gleichung der Tangente ist eine gute Näherung des nichtlinearen Kraftgesetzes für kleine Auslenkungen.
- Mit dieser harmonischen Näherung können Sie weiterrechnen :)
- Welche Schlussfolgerung können Sie aus der allgemeinen Lösung ziehen? Genauer: Wovon hängt die Frequenz der Schwingung ab? (Z.B. proportional zur Masse und zur Amplitude, etc.)
- Ausserdem können Sie nun ihre Rechnungen durch eine Messung überprüfen. Messen Sie die zur Berechnung der Frequenz nötigen Werte, führen sie eine Fehlerrechnung durch und vergleichen Sie die gemessene mit der berechneten Frequenz.
- (Um eine Fehlerrechnung durchführen zu können, müssen Sie alle Messwerte mindestens 10 mal messen. um eine statistische Streung zu haben.)