Das Potential eines Feldes: Unterschied zwischen den Versionen
(→Das Potential eines Feldes) |
(→Links) |
||
| Zeile 79: | Zeile 79: | ||
==Links== | ==Links== | ||
| − | *[http://www.schulphysik.de/java/physlet/applets/efeld3.html | + | *Darstellung eines [http://www.schulphysik.de/java/physlet/applets/efeld3.html elektrischen Potentialgebirges] (von W. Christian, Physlet-System) |
| − | *[http://www.falstad.com/vector/ | + | *Animation eines [http://www.falstad.com/vector/ Potentialgebirges], mit fließenden Kugeln von vielen verschiedenen Situationen von Paul Falstad |
Version vom 10. Mai 2012, 13:53 Uhr
Inhaltsverzeichnis
Beispiele und Versuche
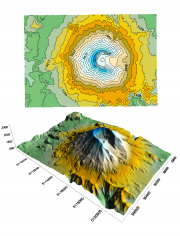
Der Potentialtrichter
Beobachtungen und Vergleiche mit Planeten / Satelliten.
Steilheit und Kraftwirkung? Je steiler, desto größer die Kraft.
Energiemenge der Kugeln? Je höher, desto mehr potentielle Energie. Je mehr Masse, desto mehr Energie. Umwandlung in kinetische Energie und zurück. Gleiches Niveau der potentiellen Energie auf einer "Höhenlinie", bei gleicher Masse.
- Ein Oszilloskop?
- Beschleunigen eines e- in einem E-Feld?
Das Potential eines Feldes
In Feldern wird Energie gespeichert. Wieviel Energie sich im Feld befindet, hängt unter anderem von der Ladung und dem Ort der Gegenstände ab. Häufig befindet sich ein "kleiner" Gegenstand in einem Feld eines "großen". Z.B. Mond und Erde oder Erde und Sonne oder Satellit und Erde. Ein Elektron kann sich in einem elektrischen Feld befinden. Nun fragt man sich:
- Wie ändert sich die Energie mit der Ladung des Probekörpers?
- Wie ändert sich die Energiemenge mit dem Ort des Probekörpers?
Potential ist die "normierte" Energiemenge also die Energie pro kg oder pro Coulomb oder pro Weber.
- [math]\varphi_g = \frac{E_{pot}}{m}[/math]
- [math]\varphi_E = \frac{E_{pot}}{Q}[/math]
- [math]\varphi_H = \frac{E_{pot}}{Q_m}[/math]
Die potentielle Energie bei konstanter Feldstärke
In der Nähe der Erdoberfläche ist die Stärke des Schwerefeldes ungefähr konstant.
- [math]F_G= m\, g[/math]
Hebt man einen Gegenstand hoch, so wirkt währenddessen die Gewichtskraft entgegen der Bewegungsrichtung und daher muss dafür Energie aufgewendet werden. Diese Energie steckt dann im Schwerefeld. (Vgl. Energieübertragung mit einer Kraft)
Fällt ein Gegenstand, so geht die Energie des Feldes in den bewegten Gegenstand.
Für die Energiemenge eines Gegenstandes der Masse m, der sich in der Höhe h über einem festgelegten Nullniveau befindet, gilt:
- [math]E_{pot}=F_G\, h = m\, g\, h[/math]
Je mehr Masse der Gegenstand hat, desto mehr Energie steckt also im Feld. Die Energie ist sogar proportional zur Masse.
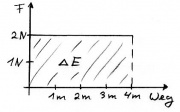
Die wirkende Kraft beschreibt die Änderung der potentiellen Energie mit der Höhe. So besagt eine Gewichtskraft von 20 N, dass man bei einem Höhenunterschied von 1m eine Energiemenge von 20J bekommt oder aufwenden muss:
- [math]F_G = \frac{E_{pot}}{h}[/math]
Ebenso eine geladene Kugel in einem Kondensator:
- [math]F_E= Q\, E[/math]
- [math]E_{pot}=F_E\, h = Q\, E\, h[/math]
- [math]F_E = \frac{E_{pot}}{h}[/math]
Die potentielle Energie bei veränderlicher Feldstärke
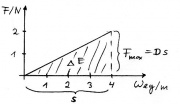
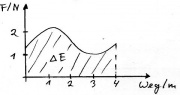
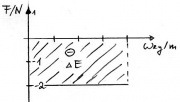
Statt [math]E = F\ s[/math] nun das Integral im Kraft-Wegdiagramm:
- [math]E = \int F(s)\, ds[/math]
und die Kraft ist die örtliche Änderungsrate der potentiellen Energie:
- [math]F = E'[/math]
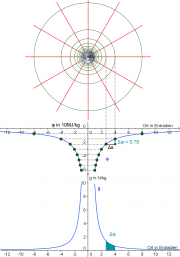
Für einen Satelliten in der Höhe h über dem Erdboden:
- [math]E_{pot}=\int_R^h F(h) \, dh = \int_R^h G\, \frac{m}{h^2} \, dh[/math]
- [math]=- G\, m \, [\frac{1}{h}]_R^h = - G\, m \, [\frac{1}{h}-\frac{1}{R}][/math]
Links
- Darstellung eines elektrischen Potentialgebirges (von W. Christian, Physlet-System)
- Animation eines Potentialgebirges, mit fließenden Kugeln von vielen verschiedenen Situationen von Paul Falstad